注重几何直观 强化逻辑推理 丰富数学模型——2018年杭州市中考数学第23题赏析及教学启示

□易良斌

（杭州市江干区教育发展研究院，浙江杭州 310020）

数学学习要以数学知识为载体，关注学生缜密的思维过程形成，借助高质量的学习资源培养学生的逻辑推理能力.杭州中考数学试卷，特别重视科学设计考试内容，强化能力立意与素养导向，优化命题结构，推动中学素质教育.其知识点分布均衡，覆盖面广，考查了学生的发现问题以及解决问题能力.尤其是对于问题的本质需要学生深入研究，试卷重视基础，核心考点突出.与以往的试题相比，今年的试题总体难度有所下降，学生对每道题都能够动手，但是如果想要得到高分甚至满分，需要有很好的基础知识和很强的解题能力.几何的考查更是重视学生的几何直观、推理能力、建立模型能力.下面以2018年杭州中考数学第23题为例，探讨数学问题解决的有效路径，分析数学问题解决在激活学生思维、发展学生关键能力的独特价值，进而唤醒教师在教学中要注重几何直观意识，强化逻辑推理能力的培养，在解决问题的过程中丰富学生的数学模型建构能力[1].

一、试题呈现

如图，在正方形ABCD中，点G在边BC上（不与点B，C重合），连接AG，作DE⊥AG，于点E，BF⊥AG于点F，设

（1）求证：AE=BF.

（2） 连 接 BE，DF，设∠EDF=α,∠EBF=β，

求证：tanα=ktanβ.

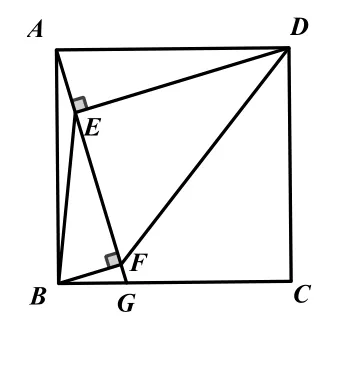
（3）设线段AG与对角线BD交于点H，△AHD和四边形CDHG的面积分别为 S1和S2，求的最大值.

这是一道相当成功的压轴题，符合数学课程标准的要求.前几年，许多地区的中考压轴题一般都在二次函数上做文章，但许多试题都是以二次函数图象为考查中心，将图象进行变化（移动、翻转），或架构几何图形，这其实是解析几何的内容，并不在初中的学习范围内，是对函数教学目标的一种误解.此题看似一道常规的动态问题，体现了函数作为研究问题、解决问题的工具性本质，准确体现了数学课程标准在二次函数方面的教学要求.

二、解题分析

第（1）题大部分学生能得满分，少部分学生失分的主要问题有两个：一是∠ADE和∠BAF相等的证明过程没有写清楚；二是用角角边证△ADE≌△ABF时错当成HL证全等.这题考查了正方形的旋转对称性.

第（2）题的书写很多，有的太简单，思维跳跃；有的又太啰唆，过程不断往结论靠，推理不严密，有些步骤是乱写，想糊弄过关.细想，过程为什么难写？原因在线段的关系转化上：一是为什么可以转化，转化的依据不清晰；二是转化的关系太多，写得比较混乱.这些乱的根源就在于思维的混乱，逻辑关系的不清晰.对于要求证的结果，我们不妨进行一些变形，即证明，其实就是要证明，而证明线段成比例的方法最常用的就是相似了，于是到图形中找BF，DE，BG，BC所在的三角形，马上就能找到Rt△BFG∽Rt△DEA.利用执果索因的办法去思考，逻辑严谨，思路顺畅，根本不需要花多少时间就能解决该题.

第（3）题首先要把图形重新画一下，把无用的内容删去，这样图形就变得更清晰，图形之间的关系能理得更清楚.设正方形ABCD的边长为1，则BG=k，分别表示出△ABG，△ABD的面积，再根据求出S1及S2，再求出S1与S2之比与k的函数解析式，求出顶点坐标，然后根据k的取值范围，即可求解.用的是代数中的二次函数模型来求最值.难点在哪？阅卷过程中发现学生根本无从下手，不知道用代数模型来解决，不知道用k来表示面积.很多学生都是猜想G在中点时，面积比最大，却缺乏利用二次函数求最值的推理过程.用字母表示面积的过程稍微复杂，S1需要用到相似的面积比例关系，还要用到等底或等高的面积关系，难度较大.还有少部分学生对三角形面积公式没掌握好，忘记乘以二分之一.

总体来说，今年的几何压轴题并不是很难，前两小题的得分情况还可以，第三小题难度较大，对学生的代数式的计算能力要求较高.

三、解法赏析

关于第（1）问.

解法1：如图1，因为四边形ABCD是正方形，所以AB=AD，∠BAD=90°，即∠DAE+∠BAF=90°，因为DE⊥AG，BF⊥AG，所以∠AED=∠AFB=90°，则 ∠DAE+∠ADE=90°，所 以 ∠BAF=∠ADE，所以△ADE≌△BAF，所以AE=BF.

解法2：如图2，延长DE交AB于P点，可得△APD与△BGA全等，然后根据全等三角形的性质，全等三角形对应边上的高相等，可得AE=BF.

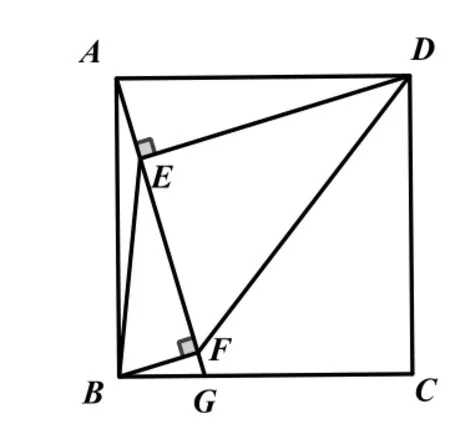
图1

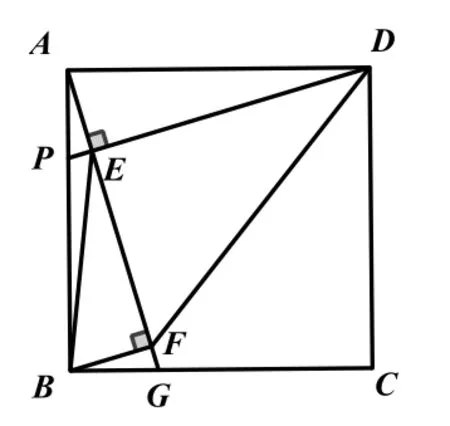
图2

关于第（2）问.

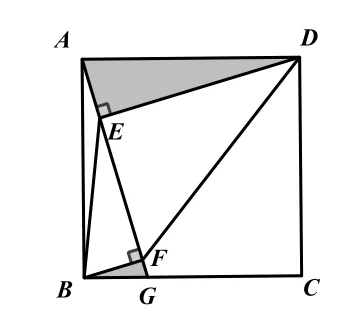
图3

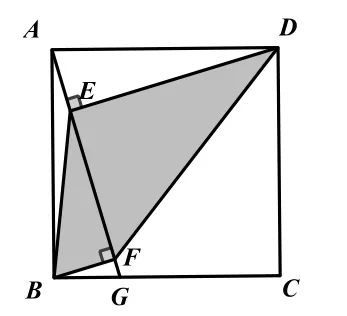
图4

关于第（3）问.

解法1：如图5，设BC=1，则BG=k，过H点作MN⊥AD，交AD于M点，交BC于N点，易得

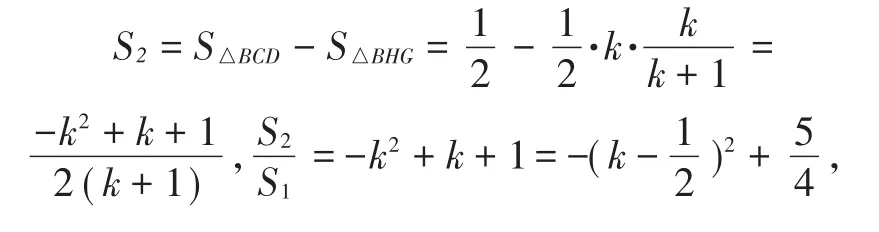
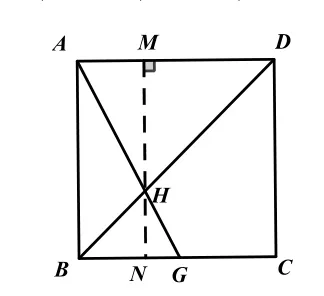
图5

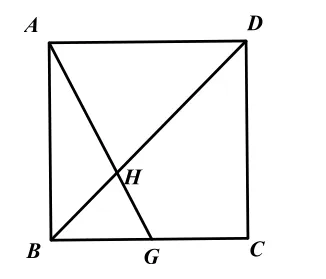
图6

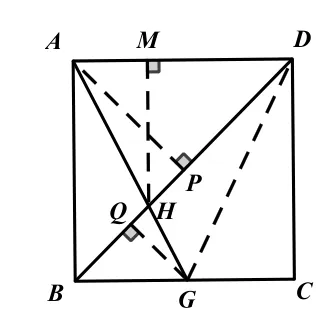
图7

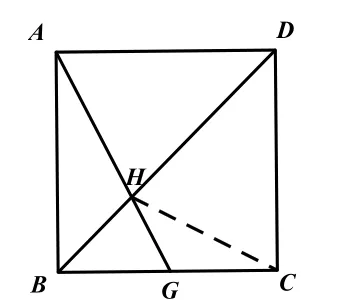
图8

解法 3：如图 7，设BC=1，则BG=k，连接DG，分别过A,G作AP⊥BD,GQ⊥BD,垂足为P,Q两点，过H作HM⊥AD，垂足为M点，参照解法由解法1，可得接下来的方法同解法1.

解法 4：如图 8，设 BC=1，则 BG=k，连接HC，由正方形的对称性可知，△AHD≌△CHD，下来的方法同解法1.

四、教学启示

（一）注重画图、析图和赏图，加深对几何问题的理解

几何是初中数学的重要组成部分，几何图形是几何的主要研究对象.在教学时，要花大力气要求学生利用三角形、圆规等作图工具精准画图.其目的是促使学生将几何学习中的文字语言、图形语言和符号语言相互转化，找准题中的关键词，如中点、任意一点、角平分线、中线、垂直、平行、平移等，加深对数学概念的理解，从而提升学生的审题能力，为顺利解题打好坚实的基础.

对题中所给的较复杂的图形，学会分解，拆分成基本图形[2].如本文中的图形中能拆分出单独的图形，如Rt△ADE，△ADF，正方形ABCD，直角梯形AGCD，四边形DFGC等，也能拆分出基本图形，如Rt△ABG和Rt△BGF组成的子母相似，Rt△ADE和Rt△ABF组成的“一线三垂直”，△ABE和△BEG是同高三角形，△AHD和△GHB组成的“8字形相似”，等等.使学生在解题时能集中精力，排除干扰，缩短学生思考时间，有效地解决问题.

在教学时，要有意识地指导学生欣赏图形，体会图形的对称美，变化美.如图9的4个图形中，可以指导学生从对称性出发欣赏美，整体是中心对称，部分是旋转对称.同时让学生说出图形之间的区别和联系，通过怎样的变换，图形可以相互转化.图形的局部又是哪类基本图形.这样不仅培养了几何直观，体会了数学美，还加强了图形之间的联系，丰富了图形的想象，为添加辅助线、解题思路的形成做好铺垫.

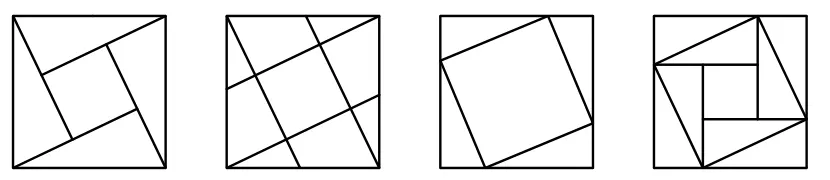
图9

（二）重视基本图形分析，提升直观想象能力

在本题的解决中，能迅速找到基本图形，就可以更快更直接得到一些有用结论.同时，在很多经典例题中，基本图形也常常伴随产生.因此，在平时的教学中，多积累一些基本图形，有利用学生解题能力的提高[3].

在教学时，加强对基本图形的结论进行梳理和小结，如对于母子形相似这个基本图形，可进行如下的梳理.局部看：单独一个直角三角形；从角看：两锐角互余；从边看：勾股定理，涉及一元二次方程；从边角看：锐角三角函数；整体看：三角形相似，相等的角，比例线段（比例中项），周长比，面积比，面积法等.在作业讲评时，经常性追问学生：看到这个图形，你能编一个什么问题？需要什么条件？还能想到什么？加强条件和结论之间的逻辑关系，图形和问题之间的预想和预判，丰富解题经验，完善知识间的重组，实现解题能力的提升.

（三）开展问题的变式教学，满足不同层次的学生需求

在几何教学时，还应对基本图形的基本问题进行精加工，深挖掘，以问题串的形式，丰富习题层次，引领学生思维向更深层次递进，满足不同层次的学生需求[4].

变式1：如图10，在正方形ABCD中，G是边BC上的一点（不与B,C两点重合），AG与对角线BD相交于H点，

（1）若AB=4，BG=1，则BH∶HD=______，HD=______，S△AHD=______.

（2）若AB=4，BG=a，则BH∶HD=______，HD=______，S△AHD=______（用含a的代数式表示）.

（3）设BG∶AB=x，S△AHD=y，求y关于x的函数关系式，并写出自变量的取值范围.

（4）尝试用列表法，画出该函数的图象，并写出这个函数的两个性质.

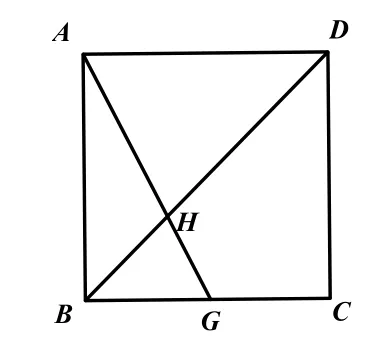
图10

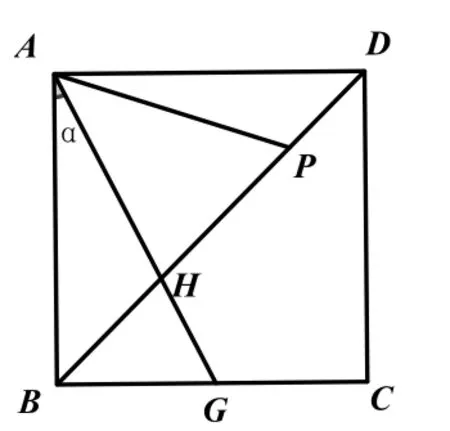
图11

通过让学生解题，然后比较前3小题之间的联系与区别，帮助学生理解从具体的数到代数式，到函数表达式，它们的计算方法是一样的，仅仅是运算的对象发生了改变，运算的结果符号化、一般化，体会从特殊到一般、从具体到抽象的过程，使知识融会贯通，完善知识体系，优化知识结构.

变式2：如图11，在正方形ABCD中，点G在边BC上（不与点B，C重合），连接AG，BD交于点H，∠BAG=α，

（2）在BD上取点P，使得∠GAP=45°，证明：SABCD=BP·DH.

第（1）题可以利用相似中的基本图形，通过边之间的转化，最后与三角函数建立联系，体现三角函数是沟通边与角之间的桥梁.也可以将研究图形的几个要素——边、角、面积通过三角函数建立联系，体现几何中边、角、面积的关系不是单向的，是多元联系的.

第（2）题可以由点动得到线段与角的关系，再由角动产生新的变化，得到面积与边之间的关系.

近几年杭州市的数学中考题让学生套用现有模型解决问题的题型越来越少，反之，对数学本质的考查增多，学生失去现有模式，得凭借对数学的理解，临场解决问题.因此，在平时的教学中，要重视学生基本活动经验的积累.教师可以让学生先行，将学生思考的作品呈现，教师围绕数学的本质进行总结和归纳，这样的教学基于学生最近发展区，学生学会的不仅仅是这堂课的知识内容，更重要的是学会思考和解题，这样就算下次遇到没有见过的问题，学生也能自己独立解决.