宁在曲中取 不在直中求——点共圆在解题中的应用

四川省德阳市中江县青市乡中心学校 龚辉伦

圆是初中继三角形、四边形学习后的唯一一种曲线型图形，它具有完美的对称性。圆的出现，为我们的几何学习提供了一种新的认识图形的方式。虽然课标要求对圆的教学要把握好一定的“度”，但由于圆这个完美图形本身具有不可替代的优势，我们仍然可以借助课本呈现的相关定理和探究活动的结论，灵活应用它们来解决一些看似与圆无关，却又深深反映出圆的性质特征的直线型题目，使复杂的问题变得简单，提高解题能力。

一、应用圆的定义，构造辅助圆来解决数学问题

试题呈现：如图1-1，四边形ABCD中，DC∥AB，BC=1，AB=AC=AD=2，则BD的长（ ）

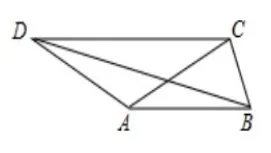
图 1-1

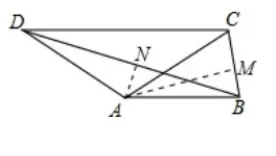
图 1-2

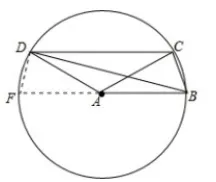
图 1-3

尝试分析：虽然本题可以根据AB=AC=AD=2这个条件，联想到等腰三角形的相关知识，通过构造全等三角形来解决（如图1-2），当然也可以通过延长BA来构造全等三角形，但这些三角形之间的边角关系比较复杂，一般基础的学生不容易看出其中的关系，很难完整地解答出来。

解题依据：在人教课本九年级上册第119页，在教学圆的定义后，课本上有如下陈述：“从画圆的过程可以看出，到定点的距离等于定长的点都在同一个圆上。”

解法生成：从题目中的描述可以看出，点B、C、D到点A的距离都等于2，满足B、C、D共圆的条件，所以，我们可以构造以点A为圆心，以AB的长为半径的辅助圆（如图1-3），结合DC∥AB的条件，易想到延长BA，将BC转化为DF，再利用圆的直径所对的圆周角是直角构造直角三角形，轻松求出BD的长为

方法总结：当题目中遇到有相等的线段且共端点时，可根据圆的定义，考虑构造辅助圆来解决问题，往往事半功倍。

二、应用同弧所对的圆周角相等，构造辅助圆来解决数学问题

试题呈现：如图2-1，在等边三角形ABC内有任意一点P，且，若三角形边长为6，求AP的最小值是多少。

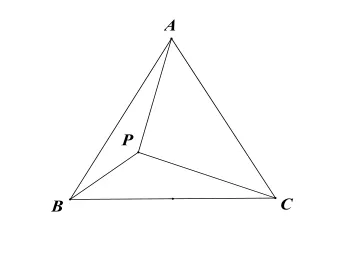
图2-1

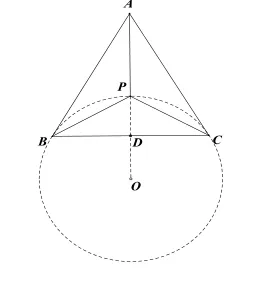
图2-2

解题依据：同弧所对的圆周角相等。

解法生成：根据点P的运动轨迹，我们可以作出过符合条件的点P及点B、C三点的圆弧，找出隐形圆，再通过圆外一点到圆上的距离最短找出P点的位置，也就是说A、P两点和隐形圆圆心O在同一条直线时，AP最短，从图2-2中不难看出，这条线也过BC的中垂线，所以，过点P作BC的中垂线，与弧的交点就是所求的P点，再通过解直角三角形，可求线段AD和PD的长，就能得到AP的最小值为

方法总结：当题目中出现了一个定角，且这个定角所对的线段是固定线段时，我们可以知道该题中可能隐含着一个过线段端点及定角顶点固定的圆，此时定线段为这个圆的一条弦，这个定角就是这条弦所对的一个圆周角，这样，我们就可以借助圆的解题优势，顺利解决直线型问题。

三、应用四点共圆的条件，构造辅助圆来解决数学问题

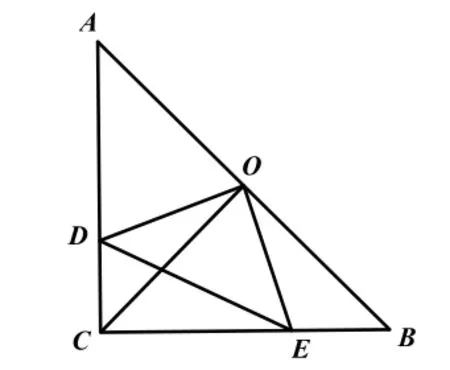
图3-1

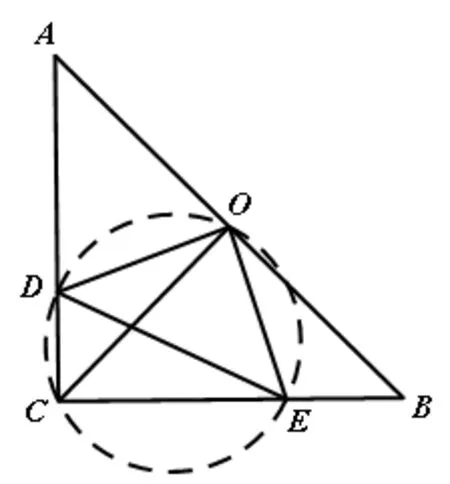
图3-2

尝试分析：在初中阶段，证明角相等的方法有很多，大多数情况下，我们能根据图形的特点，构造全等三角形来解决相关问题。但本题，我们通过观察发现，若∠CDE=∠COE成立，它们所对的线段都是CE，根据上述两类题目的经验分析，初步判断点C、D、O、E共圆，可构造辅助圆来解决相关问题。

解题依据：人教版课本九上P119的活动二，从“探究四点共圆的条件”结果所知，当四边形对角互补时或者一个外角等于四边形的内对角时，这个四边形是一个定圆的内接四边形，即四边形的四个顶点共圆。

方法总结：当四边形有一组对角互补时，我们可以利用四点共圆的条件，构造辅助圆来解决相关问题。同时，在本题中，由于对角所在的两个角都是直角，我们根据90°的圆周角所对的弦是直径，不但可以判断D、C、E、O四点共圆，而且还可以得到线段DE就是这个辅助圆的直径。

数学转化思想就是要对条件和结论进行转化，将分散转化为集中、将隐性转化为显性。从以上三种构造辅助圆的情况可以看出，这些构造方法涉及圆的定义及判定，均有课本定理或者探究活动的结论为据，符合数学课标对圆教学要有“度” 的要求，且中考中不乏此类题目的呈现，所以在教学中，我们要培养学生的合情推理能力，不断积累知识经验，提高解题能力。