蒙特卡洛模拟Fe-Cr合金的磁团簇展开

，，，

(南京邮电大学电子科学与工程学院，江苏 南京 210003)

1 前 言

众所周知，与相应的固体单晶相比，过渡金属原子组成的小尺寸团簇往往具有不同的几何结构和磁学性质，如目前研究的二元合金在Cr成分为8～9%时，有着较低的活性。一般认为这些性质起源于体系有限的尺寸、较低的维度和较大的比表面积。Kohl和Bertsch及Tatsuki等[1]分别在小尺寸Fe和Cr团簇中发现了非共线磁性。Fe-Cr合金团簇可以展示出丰富的几何结构、电子结构以及更为奇特的磁学性质。因此，对Fe-Cr合金的热力学性能有全面的了解，将有助于开发性能更加优良的新型材料。

计算机模拟方法，已被广泛应用于团簇热力学性质的理论研究。Fe-Cr合金中主要有两方面对体系的能量有影响，一是磁矩方向，另一个是合金中原子所处的位置[2]。我们现有的方法，比如团簇模型CE(cluster expansion)[3]，未考虑磁矩方向，故无法分辨以上两方面对体系能量造成的影响。磁团簇展开模型MCE(magnetic cluster expansion)[4-5]作为CE的推广，明确地考虑到磁矢量变量，能同时描述结构无序和磁性能两方面，并且能够适用于任何大小的原子团簇。对于纯Fe，考虑原子间最近邻和次近邻相互作用能很好地描述材料的基本性能[6]，但对于Fe-Cr和Cr合金，会有较明显的反铁磁性，必须考虑长程相互作用(原子间最高达到第5近邻)。MCE模型中包含了短程(最高达到次近邻)非磁性相互作用和长程磁性相互作用，相比现有的CE模型，MCE模型更适用于对Fe-Cr合金的研究。

2 磁团簇模型(MCE)介绍

MCE模型的体系能量取决于离散的CE变量以及有大小和方向的经典原子磁矩，也就是说，MCE模型的哈密顿量是传统的CE项、关于原子磁矩大小的自由能项和类似于海森堡模型的磁性相互作用项的总和。最简单的MCE哈密顿量表达式类似于海森堡-朗道形式：

(1)

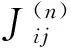
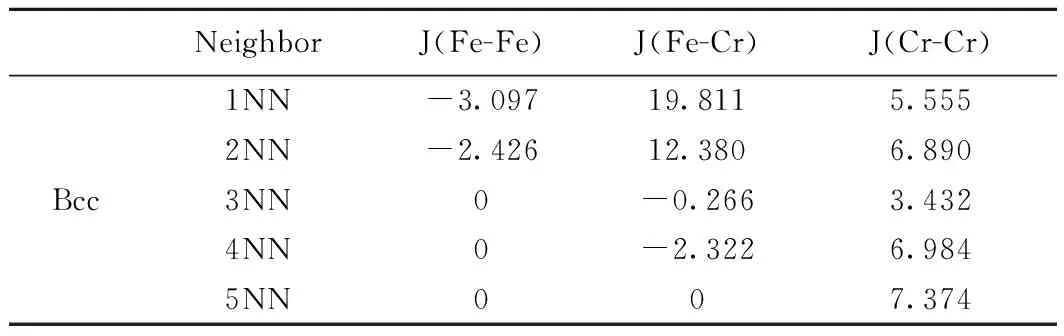
表1 Fe-Cr MCE哈密顿量的相互作用系数Table 1 Magnetic interaction parameters for Fe-Cr MCE Hamiltonian (meV)

蒙特卡洛(Monte Carlo)方法[7-8]即统计试验方法，用于解决庞大系统中的困难问题。就Fe-Cr，将Fe记做+1，Cr记做-1，蒙特卡洛算法如下：

(1)假设全部格点设置为+1，随机选择点格的一个座i，计算出初始能量H(S)，考虑此座点的自旋Si进行反转，算出反转后的能量H(S)′。

(2)计算该反转相联系的能量改变ΔH=H(S)-H(S)′。

(3)计算该反转的转移概率W，转移概率函数为：

(2)

(4)抽取一个在[0,1]区间均匀分布的随机数x。

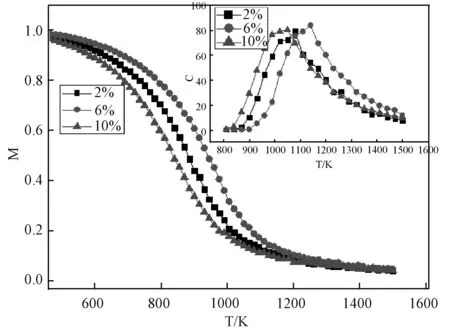
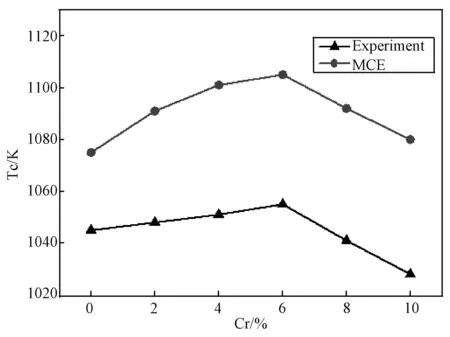
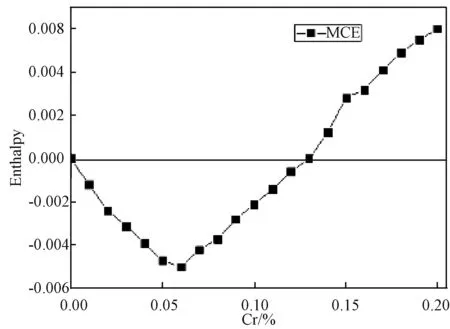
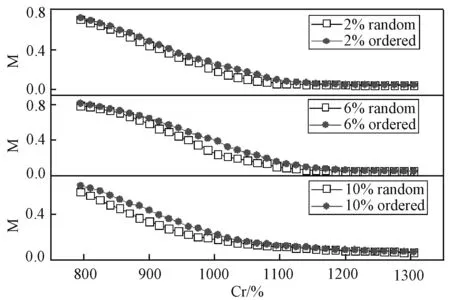
(5)如果x

(6)重复(1)到(5)，一旦对点格上的所有点都给过一次反转方向的机会，就完成一次扫描。

3 结果和讨论

本文蒙特卡洛模拟是在包含了54000个原子的晶胞中进行的(bcc结构)，每个原子预热步数为10000，取样步数为3000，每隔30步抽一个样本。得到在Cr组分较低(0～10%)的情况时，磁化强度随着Cr组分变化的Fe-Cr合金的磁化曲线(当Cr含量超过10%时，实验和理论计算均表明将出现较为明显的相分离现象，且朗道系数也会出现偏离，所以不再考虑)。 图1是归一化的磁化曲线，可以看出在Cr含量较低时(0～10%)，Fe-Cr合金的居里温度经历了先升后降的变化，当Cr含量为6%达到最大值。

图1 无序Fe-Cr的磁感应强度随温度变化的曲线图(插图为相应的比热变化图)Fig.1 Magnetic induction intensity of Fe-Cr curve with temperature changes (The specific heat is shown in the inset)

由于相变点的比热存在突变，磁转变的准确温度可以通过比热的最大值来确定，见式(3)：

(3)

Fe-Cr合金比热随Cr成分的变化曲线，如图1插图所示。根据MCE的结果可知，纯铁的居里温度约为1075K，比实验结果高了30K，其它含量Fe-Cr合金的模拟居里温度总体上约比实验数据高出30～50K[8]，但MCE模拟和实验结果随成分的变化趋势是一致的，如图2所示。

图2 MCE模拟结果和实验结果对比图Fig.2 Comparison of experimental results and simulations

为了研究转变温度随成分的变化，我们计算了合金体系的焓值。焓是热力学中表征物质系统能量的一个重要状态参量，与变化的途径无关，只要体系的状态定了，焓就有唯一确定的值。MCE模型中晶体中的焓[8]可用下式表示：

E(σi)=J0+∑αDαJαφα(σi)

(4)

其中，Jα是团簇展开系数，根据对称性简并因子Dα可以给出团簇的数目，对式(4)进行数值反演，计算不同Cr原子占位方式的第一性原理数据[9]，最终拟合获得团簇展开系数和Dα[8]。在本文中，我们将J0=0，J1=0分别对应纯Fe和低成分Cr时混合焓的计算。我们建立测得居里转变温度相同的模型，找到Cr原子无序掺杂时，不同Cr成分下，从2000 K降温到0 K，体系最低的混合焓，得到结果见图3。在低成分时，混合焓是一个负值，此时Fe-Cr合金结构稳定；混合焓随着Cr的增加，先降低后上升，在Cr含量为6%时到达一个最小值，此时结构最为稳定；当Cr含量为12%时，混合焓符号为正，从而出现相分离的趋势，因此，只需研究Cr含量低于10%的情况。

图3 通过MCE模型获得的Fe-Cr体系最低的混合焓Fig.3 Lowest enthalpies of mixing of the FeCr system found by MCE

在同一含量下，Cr原子有序和无序排列的磁相变转变温度，分别选取Cr含量为2、6和10%进行模拟。在纯Fe体心立方中，将8个正方体的中心处替换成Cr原子，总共有1372个Cr，体系总共有28×28×28个原子，此时为Fe-6.25%Cr；Cr含量为2%时，每行首尾空2个点，每隔4个点放一个Cr，这样有6×6×6=216个Cr原子，里面再嵌套6×6×6个Cr原子，此时Cr原子数目为432个；10%时，在已有的6%基础上，再嵌套一个9×9×9的Cr，此时Cr原子数有2101个，占总量的10%左右，蒙特卡洛模拟步骤同上。

图4 有序和无序结构的磁化强度与温度图Fig.4 Magnetization of ordered and random Fe-Cr structures as a function of temperature

图4是不同浓度下居里温度附近有序和无序态磁化曲线的比较，图中可见，在同一组分的样品中，有序结构的居里温度略高于无序样品，特别是在Cr含量为6%样品中的差别最大。这反映了无序态下Cr原子形成团簇的几率增加，Cr-Cr之间反铁磁相互作用能够部分抵消磁矩，从而降低了相变温度。居里温度随成分的变化而变化，反映出离散的Cr原子与铁基体之间的铁磁相互作用。在我们对MCE系数的设定中(表1)，Fe-Cr最近邻和次近邻的海森堡相互作用系数远比相应的Fe-Fe系数要大得多，Fe-Cr相互作用比Fe-Fe相互作用强，因此，在Cr成分较低时，Cr原子替换掉合金中Fe原子的位置，Cr原子和最近邻的Fe原子配对，增强了整个合金中铁基体的铁磁有序，降低了体系的能量，同时Cr原子之间的平均距离足够远(大于等于两倍的晶格常数)[8]，从而有利于铁磁相的稳定；随着体系中Cr原子数目的增加，Cr原子越来越容易找到最近邻和次近邻的相互作用的Cr原子，系统混合焓也随着Cr成分增加而开始增加，增加了相分离的几率，特别是在无序掺杂的情况下Cr原子容易聚集形成团簇，Cr-Cr相之间的反铁磁相互作用将导致磁阻挫效应的产生，削弱了铁基体的铁磁相互作用从而降低居里温度。

4 结 论

本文采用MCE法研究在Cr含量较低时Fe-Cr合金的磁性性能，此方法考虑了原子的磁矩变化和无序排列的影响，能够很好地用来研究合金的磁性能。模拟结果表明，在Cr最佳掺杂浓度为6%时有最高的居里温度。结合焓值随成分的变化，认为在Cr成分较低时，Fe-Cr之间的铁磁性占据主导地位，随着Cr的不断增加，Cr原子越来越容易找到最近邻和次近邻的相互作用的Cr原子，Cr-Cr之间的反铁磁削弱了铁基体的铁磁相互作用；同时，有序结构的居里温度比无序要高，这些结论有助于FeCr合金及相关材料的制备。