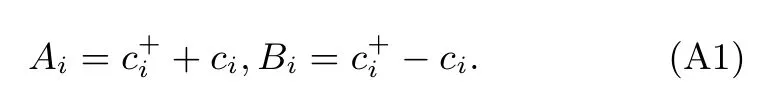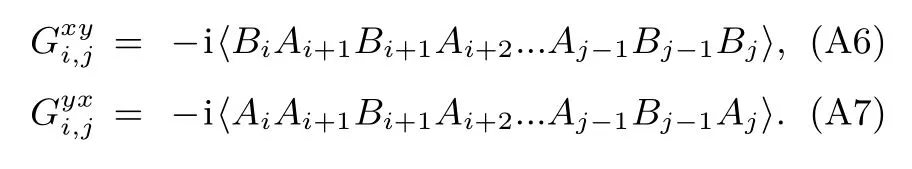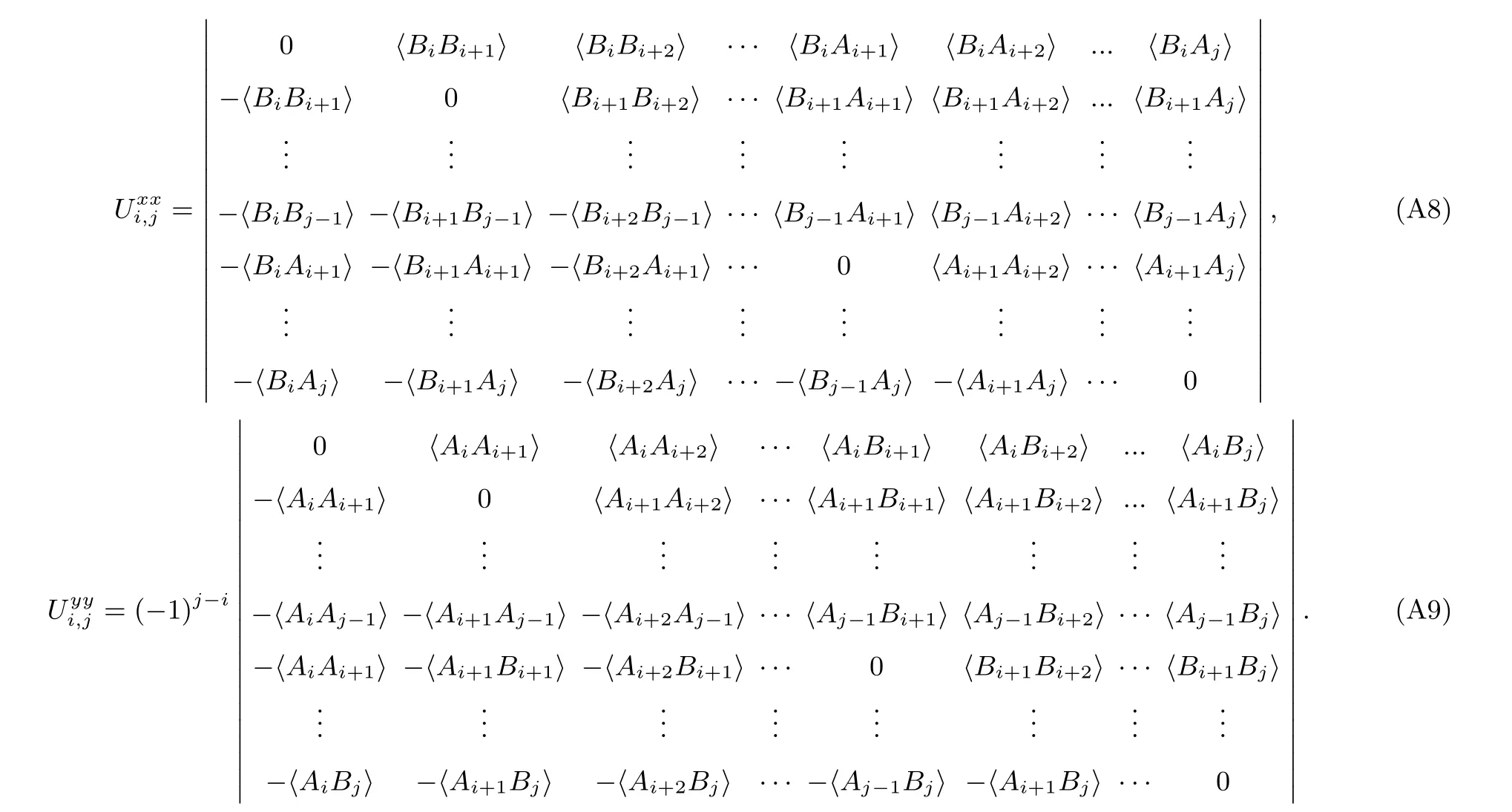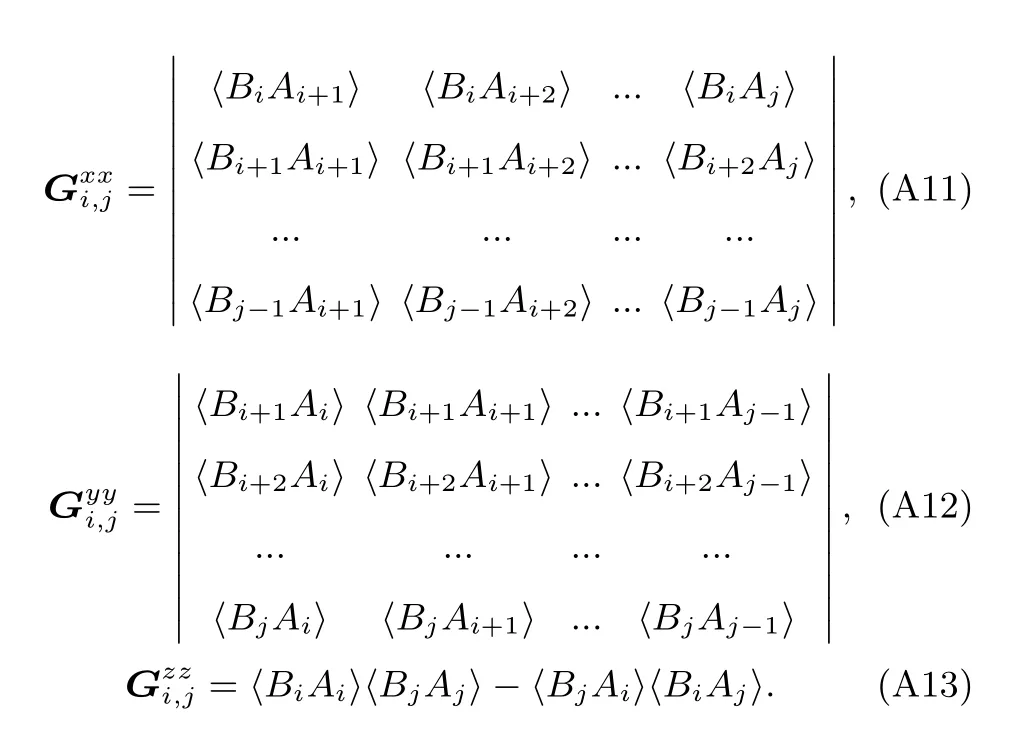具有Dzyaloshinskii-Moriya相互作用的XY模型的量子相干性∗
2018-10-29伊天成丁悦然任杰王艺敏尤文龙4
伊天成 丁悦然 任杰 王艺敏 尤文龙4)†
1)(苏州大学物理与光电·能源学院,苏州 215006)
2)(常熟理工学院物理系,常熟 215500)
3)(陆军工程大学通信工程学院,南京 210007)
4)(苏州大学,江苏省薄膜材料重点实验室,苏州 215006)
(2018年2月13日收到;2018年4月3日收到修改稿)
研究了具有Dzyaloshinskii-Moriya(DM)相互作用的一维横场XY自旋链的量子相变和量子相干性.采用约旦-维格纳变换严格求解了哈密顿量,并描绘了体系的关联函数和相图,相图包含反铁磁相、顺磁相和螺旋相.利用相对熵和Jensen-Shannon熵讨论了XY模型的量子相干性.研究发现,相对熵与Jensen-Shannon熵所表现的行为都可以很好地表征该模型的量子相变.非螺旋相中量子相干性不依赖DM相互作用,而在螺旋相DM相互作用对量子相干性有显著影响.此外,指出了在带有DM相互作用的这一类反射对称破缺体系中关联函数计算的常见问题.
Here,0 6 γ 6 1 is the anisotropic parameter,h is the magnitude of the transverse magnetic field,D is the strength of Dzyaloshinskii-Moriya(DM)interaction along the z direction.The limiting cases such as γ=0 and 1 reduce to the isotropic XX model and the Ising model,respectively.We use the Jordan-Winger transform to map explicitly spin operators into spinless fermion operators,and then adopt the discrete Fourier transform and the Bogoliubov transform to solve the Hamiltonian Eq.(8)analytically.When the DM interactions appear,the excitation spectrum becomes asymmetric in the momentum space and is not always positive,and thus a gapless chiral phase is induced.Based on the exact solutions,three phases are identified by varying the parameters:antiferromagnetic phase,paramagnetic phase,and gapless chiral phase.The antiferromagnetic phase is characterized by the dominant x-component nearest correlation function,while the paramagnetic phase can be characterized by the z component of spin correlation function.The two-site correlation functions Gxyr and Gyxr (r is the distance between two sites)are nonvanishing in the gapless chiral phase,and they act as good order parameters to identify this phase.The critical lines correspond to h=1,γ=2D,andWhen γ =0,there is no antiferromagnetic phase.We also find that the correlation functions undergo a rapid change across the quantum critical points,which can be pinpointed by the first-order derivative.In addition,decreases oscillatingly with the increase of distance r.The correlation functionfor γ=0 oscillates more dramatically than for γ =1.The upper boundary of the envelope is approximated as ∼ r−1/2,and the lower boundary is approximately∼ r−3/2,so the long-range order is absent in the gapless chiral phase.Besides,we study various quantum coherence measures to quantify the quantum correlations of Eq.(8).One finds that the relative entropy CREand the Jensen-Shannon entropy CJSare able to capture the quantum phase transitions,and quantum critical points are readily discriminated by their first derivative.We conclude that both quantum coherence measures can well signify the second-order quantum phase transitions.Moreover,we also point out a few differences in deriving the correlation functions and the associated density matrix in systems with broken reflection symmetry.
1 引 言
量子相干和量子纠缠是量子力学最基本的两个特性,其根源在于量子态的叠加原理,即单个量子态可由多个不同态以不同的方式相干叠加得到.量子相干和量子纠缠被认为是量子物理和量子信息的核心,是实现各种量子任务(如量子远程通信和量子计算等)的量子资源,是量子信息科学的优势所在.这两种现象尽管概念完全不同,却有着紧密的联系.相干性和纠缠可以通过运算等效[1].目前,作为一种对量子叠加性的量化,量子相干性已经成为处理量子信息的一种重要的手段[2].研究表明,量子纠缠可以被认为是相干性的一种体现,反之则不成立.例如,两量子比特的直乘态没有纠缠,只有相干. 物理学家对量子纠缠的研究已有几十年,成果斐然[3].量子纠缠在量子科技中发挥着不可或缺的作用,比如可以实现密钥共享[4]、量子密码术[5]和量子克隆[6]等.与量子纠缠相比,人们对量子相干领域的研究还较少.而借鉴量子纠缠领域的研究成果可以大大加深对量子相干性的研究.近年来,人们应用量子信息的概念,如量子纠缠[7−11]、量子失谐[12,13]、保真率[14,15]来描述量子相变,拓展了对量子临界行为的认识.人们发现量子纠缠在非临界区满足面积定理,而在临界点表现出对数发散行为[16].为此,利用量子相干性来研究强关联体系的量子相变,有助于理解凝聚态系统中更广泛而深刻的行为.同时,对量子相干性的深入研究不仅对量子信息的发展有着重大的意义,也可以促进对量子力学基本问题的理解.
本文研究具有Dzyaloshinskii-Moriya(DM)相互作用的自旋1/2的XY模型的量子相干性.XY模型是低维量子系统的一个重要模型,它在1961年就被Lieb等[17]严格求解.XY模型具有非常广阔的变化范围,它包含了Ising模型、各向同性XX模型以及各向异性XY模型,具有非常丰富的物理内涵.许多复杂模型都可以借助一系列的方法映射到此模型上来解决问题,它等价于二聚化的XX模型[18].不仅如此,众多材料也能实现有效的XY模型.例如,Cs2CoCl4是沿着b轴的自旋1/2的准一维XY自旋链[19];将钴原子链蒸发在Cu2N/Cu(100)衬底上可以形成有效的XY模型[20].近年来,人们对DM相互作用具有浓厚的兴趣,对于具有DM相互作用的反铁磁性的材料进行了广泛的研究.DM相互作用是存在于磁性材料中的一种非对称的交换作用,源于自旋轨道耦合[21,22].在一级近似下,DM相互作用可以写成Dij·(σi× σj),这里Dij称为DM矢量.DM 相互作用可以使一些材料表现出新的性质,比如引起亚铁磁绝缘体Cu2OSeO3的螺旋自旋基态和铁电性质的变化[23−25],诱发多铁材料BiFeO3的摆线状磁结构[26].DM相互作用的存在使得电子自旋共振[27]和电场调制[28]等技术可以应用在磁性化合物上.这些神奇的现象激发了理论研究者的广泛兴趣[29−36].
本文的结构如下:第2部分介绍具有DM相互作用的一维XY模型,计算该模型的能谱和基态性质,并给出XY模型在不同情况下的相图;第3部分讨论XY模型的关联函数;第4部分利用相对熵和Jensen-Shannon熵讨论XY模型的量子相干性;第5部分给出最终的结论.
2 模型和相图
在此引入XY模型的哈密顿量:
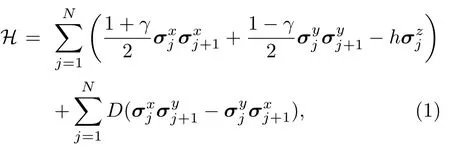
其中γ表示描述各向异性程度的参数,h表示磁场的大小,D表示沿着z轴的DM相互作用强度,表示位于格点i上自旋的泡利矩阵的α分量,N为总格点数.本文选择周期边界条件,即σN+1=σ1.当γ=0时,模型(1)为各向同性的XX模型;当γ=1时,模型(1)简化成Ising模型.利用约旦-维格纳变换做进一步处理:
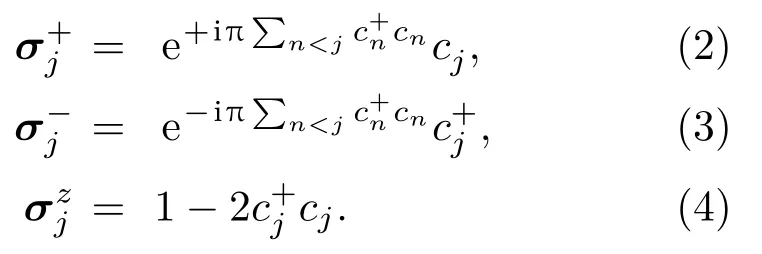
这里需要借助产生算符σ+和湮灭算符σ−,其定义为σ±≡(σx±iσy)/2.由此,上述哈密顿量(1)式可以被写成关于无自旋费米子的产生算符和湮灭算符的二次型:

由于哈密顿量(1)式具有平移不变性,可以通过傅里叶变换将方程(5)转换到动量表象.最后,利用波戈留波夫变换再进行对角化处理,这样可以得到基态能量的精确解.最终哈密顿量可以变换为对角化的形式:
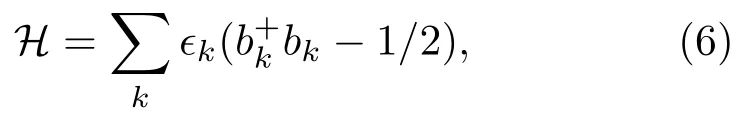
其中
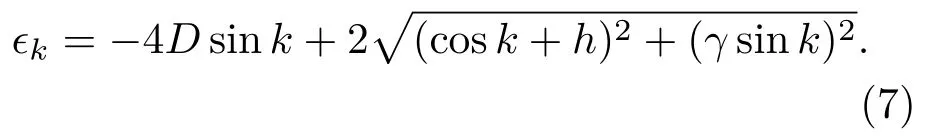
图1显示了h=0.5,γ=1时D取不同值时的激发谱ϵk,十分清楚地反映了能谱随DM相互作用变化的趋势.当D=0时,能带存在能隙∆ ≡ minkϵk.这时基态|ψ0中所有动量k上的电子占据数为0,即bk|ψ0=0.随着D的增加,能隙∆变得越来越小.当D=0.5时,ϵk在某一个非公度的动量kc等于0,能隙关闭.当D>0.5时,部分能谱变成负数,能隙消失,费米面上有两个交点kL和kR.对于一般情况,不难从(7)式得到

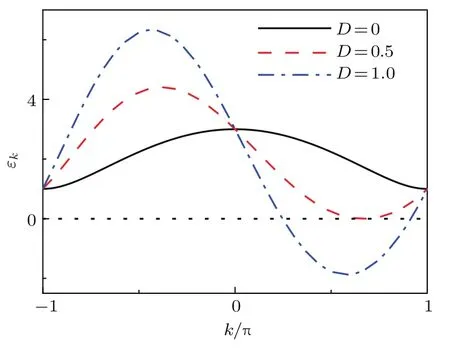
图1 h=0.5,γ=1时的激发谱Fig.1.Excitation spectra for h=0.5,γ=1.
换句话说,对于kL6 k 6 kR,激发谱ϵk是负的,基态中所有负能态被占据,即[33].
众所周知,当DM相互作用不存在的时候,h=1对应反铁磁相-顺磁相的Ising相变,此时能隙在动量kc=0上闭合.γ=0且h 6 1则是一条各向异性相变线.以上相变都属于二级量子相变.根据能隙关系,在图2中给出了γ=1,γ=0.5,γ=0时对应的相图.从图2中可以看出,在一般情况下XY模型存在三个相.区域I和区域II是有能隙相,能隙在h=1关闭.区域III为无能隙相,其与区域I和区域II的相变线所对应的解析式分别为γ=2D和不失一般性,下面主要关注γ=0和γ=1的情况,因为后者代表0 6 γ 6 1的一般情况.
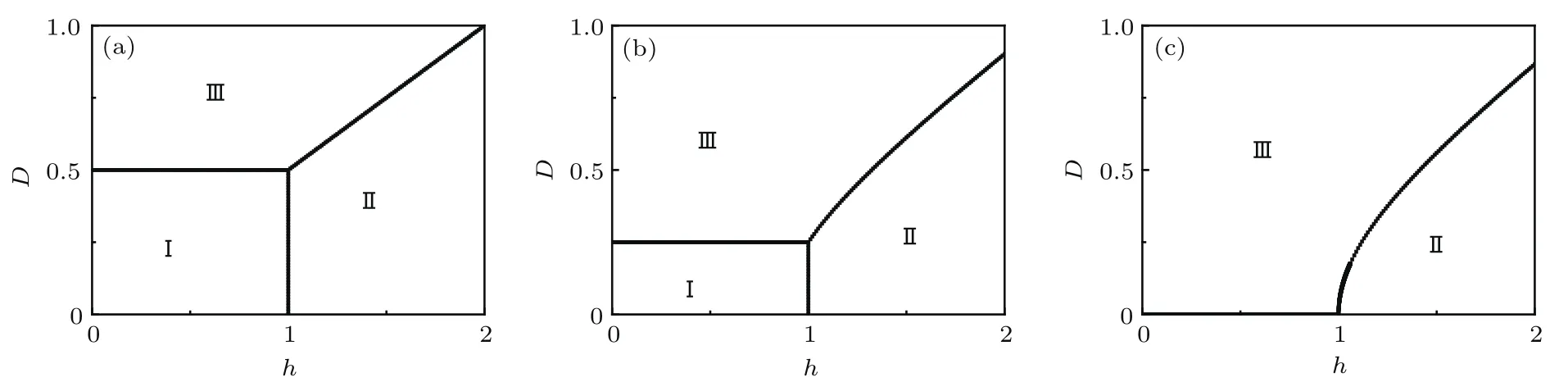
图2 不同γ所对应的相图 (a)γ=1;(b)γ=0.5;(c)γ=0;区域I,II,III分别代表反铁磁相、顺磁相和螺旋相Fig.2.Phase diagram with respect to γ:(a) γ =1;(b) γ =0.5;(c)γ =0.Region I,II and III correspond to antiferromagnetic phase,paramagnetic phase and chiral phase,respectively.
3 关联函数
为了表征不同相,选取两格点之间的关联函数作为序参量来描述系统基态的性质,定义关联函数≡其中α,β=x,y,z.由于该系统具有平移不变性,因此关联函数的大小仅与i,j两格点之间的相对距离有关,而与两个格点所在的具体位置无关,所以可以将简记为其中r=i−j.对于一般的展开形式可以表示为法夫式(Pfaffian)[37,38].换句话说,可以写成2n×2n(n≡|j−i|)维反对称矩阵的行列式,更进一步的细节性的讨论见附录A.
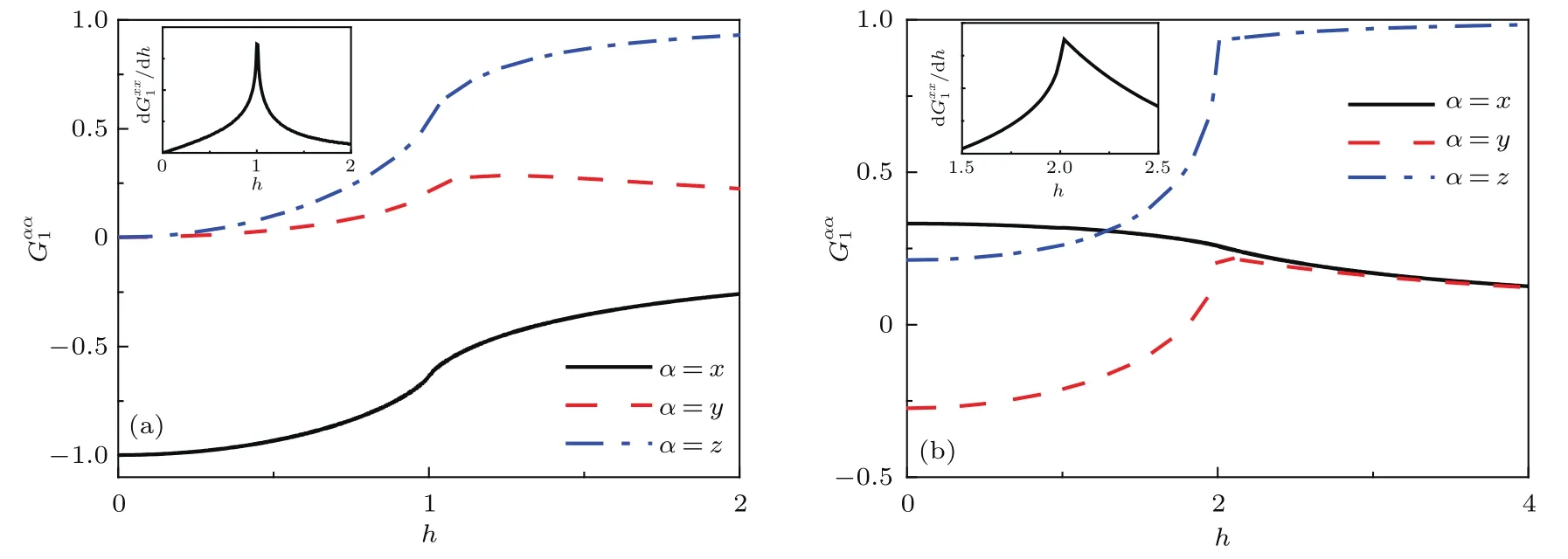
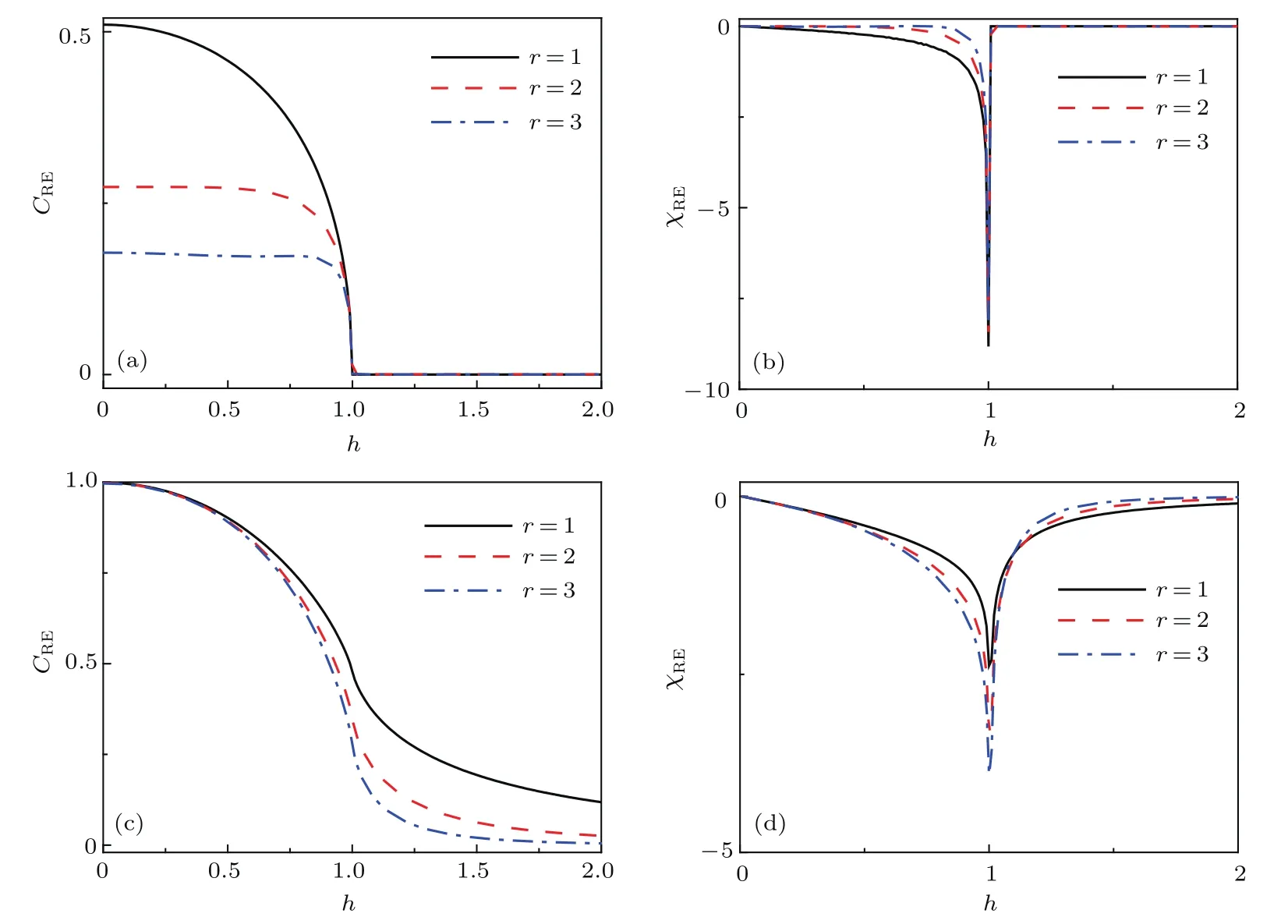
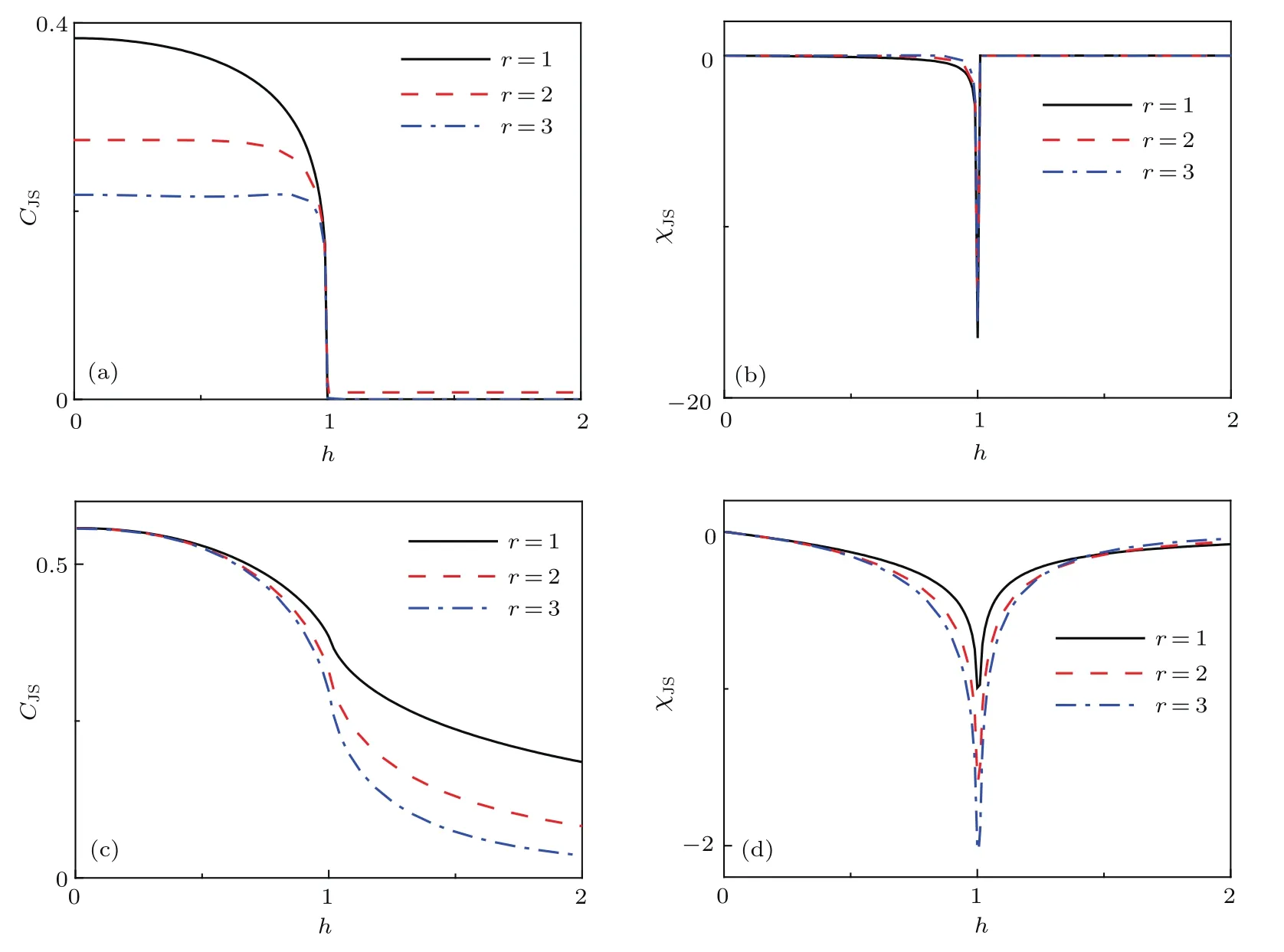
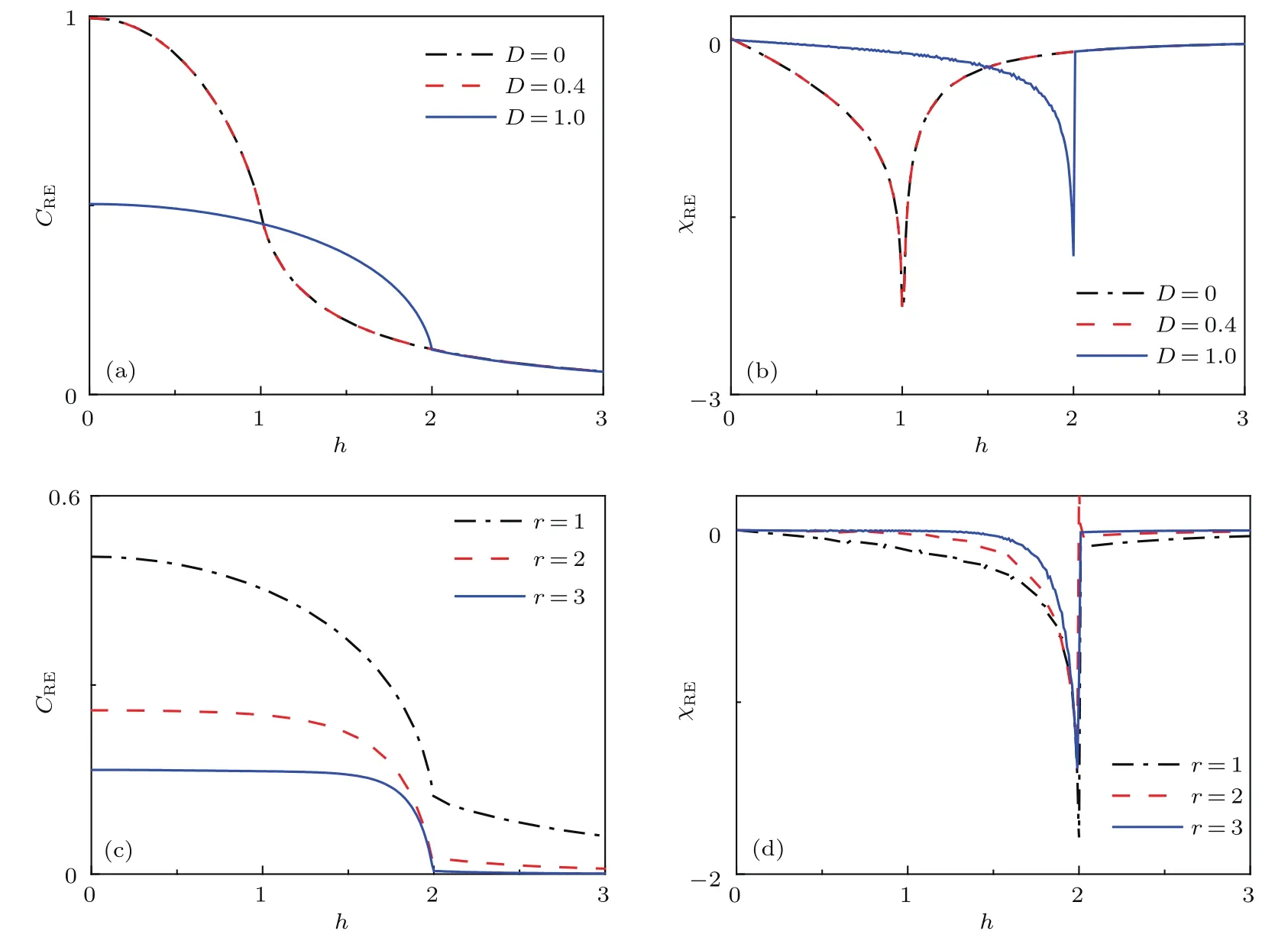
首先考虑各个分量的最近邻关联.不失一般性,在图3中展示了γ=1的两条参数路径:D=0和D=1.在图3(a)中,可以看出x分量的最近邻关联随着磁场强度h的增加从−1渐渐趋近于0,而y和z分量的最近邻关联随h的增加从零开始呈增长之势,这表明区域I为反铁磁相.三种最近邻关联在量子相变点处都发生了突然的变化.如图3(a)插图所示,的一阶导数在h=1有一个明显的尖峰,意味着此处发生了二级量子相变.经过相变点后,和都逐渐趋近于0,而则渐渐地趋近于1,说明区域II为顺磁相.如图3(b)所示,由于DM相互作用的出现,临界磁场hc的位置发生了明显的变化,从D=0时的hc=1移动到D=1时的hc=2.类似地,的一阶导数在hc=2也呈现了一个尖峰(见图3(b)插图),这一结果与图2中的相变线一致.值得注意的是,当h 除了最近邻的两点关联,接下来考虑长程的两点关联.Barouch和McCoy[38]研究了横场XY模型的磁化强度和关联函数.Its等[39]考虑横场XX模型的非零温关联.研究表明关联函数的渐进行为(r→∞)可以写成 图3 最近邻关联函数随着h的变化 (a)γ=1,D=0;(b)γ=1,D=1;插图为的一阶导数Fig.3.The nearest correlation functionwith respect to h for:(a)γ=1,D=0;(b)γ=1,D=1.Insets show the first-derivative of 图4 (a)γ=1时随着h和D变化的情况;(b)γ=1时随着h和D变化的情况Fig.4.(a)as a function of h and D for γ =1;(b)as a function of h and D for γ =1. 图5 关联函数的绝对值随着距离r的变化(a)D=0,γ=0;(b)D=0,γ=1;(c)D=1,γ=0;(d)D=1,γ=1Fig.5.The absolute value of the correlation functionwith respect to r:(a)D=0,γ=0;(b)D=0,γ=1;(c)D=1,γ=0;(d)D=1,γ=1. 在凝聚态理论中,量子相变需要构建合适的序参量来描述,如上文提及的自旋关联函数,但是往往序参量是事先不知道的.量子相变发生在零温时体系的量子关联随着参数的调节发生了突然的变化,对系统的量子关联进行量化和表征已经成为研究热点之一.随着量子信息的发展,一些量子信息的概念被移植到凝聚态领域,如量子纠缠、量子失谐、保真率也被用来描述量子相变[41−43].自然而然,量子相干性是一种典型的量子关联的刻度. 其中 值得一提的是,很多先前的研究[44,45]在考虑(13)式和(14)式时默认了= 0和=0,这与图4的结论是不符合的.这里要强调=0和=0只在纯实数哈密顿量的条件下才成立,对于哈密顿量中含有DM相互作用或者XZY-YZX类三体相互作用是不成立的[31,46,47],甚至一些文献[48]忽略了此时计算要利用原始公式(A10)(见附录A),而不是(A13)式. 相对熵是Baumgratz等[49]依据资源理论引入的相干性的量化指标,其计算公式为 其中S(ρ)= −Tr(ρlog2ρ).S(ρ)代表密度矩阵ρ的冯·诺依曼熵,S(ρdiag)则代表密度矩阵清除非对角项之后得到的新密度矩阵的冯·诺依曼熵.研究表明,XY模型的量子相变临界点可以用量子相干率(coherence susceptibility)的奇异性来描述[50],其定义为相对熵的一阶导数 图6显示了在不同γ的情况下不同近邻程度的相对熵CRE以及相干率χRE随着磁场h变化的情况.当γ=0的时候,不同距离的两量子比特的相对熵具有相似的变化趋势(见图6(a)).随着h的增加,它们都呈现出减小的趋势.距离r越大,相对熵越小.不同的是,最近邻的相对熵衰减相对比较明显,次近邻以及更远近邻的相对熵起初保持一定的鲁棒性.当h靠近1的时候,所有距离的两量子比特相对熵都急剧衰减为0.在顺磁相中相对熵一直保持为0.图6(c)中,当γ=1时两量子比特的相对熵随着h的增长而减小,由于长程序的存在,不同距离r差别不大.同样在h=1处CRE有一个急剧的下降.与γ=0的情况不同,进入顺磁相后χRE仍然存在,且绝对值随着h的增加而减小.从图6(b)和图6(d)中可以看出,在h=1处,量子相干率χRE出现了一个奇点,表明在此处体系的相干性有一个剧烈的变化,即发生了量子相变. 图6 D=0时相对熵CRE和量子相干率χRE随h的变化 (a)γ=0时的CRE;(b)γ=0时的χRE;(c)γ=1时的CRE;(d)γ=1时的χREFig.6.The relative entropy CREand the quantum coherence susceptibility χREfor D=0:(a)CREfor γ =0;(b) χREfor γ =0;(c)CREfor γ =1;(d) χREfor γ =1. 图7 D=0时Jensen-Shannon熵CJS和量子相干率χJS随h的变化 (a)γ=0时的CJS;(b)γ=0时的χJS;(c)γ=1时的CJS;(d)γ=1时的χJSFig.7.Jensen-Shannon entropy CJSand the quantum coherence susceptibility χJSfor D=0:(a)CJSfor γ =0;(b) χJSfor γ =0;(c)CJSfor γ =1;(d) χJSfor γ =1. 图8 γ=0时不同D的情况下相对熵CRE和量子相干率χRE随着h的变化 (a)最近邻情况下的CRE;(b)最近邻情况下的χRE;(c)D=1时不同近邻情况下的CRE;(d)D=1时不同近邻情况下的χREFig.8.The relative entropy CREand the quantum coherence susceptibility χREwith respect to D for γ =0:(a)CREfor the nearest-neighbor qubits;(b)χREfor the nearest-neighbor qubits;(c)CREfor Different distances r between two qubits with D=1;(d)χREfor Different distances r between two qubits with D=1. 除利用相对熵以外,还可利用Jensen-Shannon熵讨论XY模型的量子相干性[51].Jensen-Shannon熵的定义与相对熵类似: 同样,其相干率亦定义为 图7显示了在不同γ的情况下Jensen-Shannon熵CJS以及所对应的相干率χJS随着磁场h变化的情况.Jensen-Shannon熵所表现的行为与相对熵定性上十分类似,都可以体现出在h=1处,系统发生了量子相变,所以接下来主要通过相对熵来研究量子相干性. 图8展示了γ=0时两量子比特的相对熵在不同DM相互作用下的情况,同时给出了各自对应的量子相干率的变化规律.结果表明有限的D只能改变临界磁场hc的大小,而不改变临界行为.图8(a)中最近邻两量子比特的相对熵CRE随着h的增加而单调减少.从图8(c)可以看出D=1时,不同近邻程度的两量子比特的相对熵CRE有着十分类似的变化趋势,都是先随着磁场的增加缓慢下降,然后在相变点的位置急速下降.在远离相变点的位置,最近邻情况下的相对熵随磁场的变化相对比较明显,而次近邻和次次近邻则相对比较缓慢.当磁场h驱使系统进入顺磁相,CRE都消失为0.图9展示了γ=1时与图8相对应的情况,同样可以看出,两量子比特的相对熵CRE随着h的增加而减少.令人惊讶的是,当D=0时,CRE与h的依赖关系和D=0.4时重合.确切地说,非螺旋相中CRE不依赖D.而在螺旋相中,D对CRE有显著影响,见图8(a). 图9 γ=1时不同D的情况下相对熵CRE和量子相干率χRE随着h的变化 (a)最近邻情况下的CRE;(b)最近邻情况下的χRE;(c)D=1时不同近邻情况下的CRE;(d)D=1时不同近邻情况下的χREFig.9.The relative entropy CREand the quantum coherence susceptibility χREwith respect to D for γ =1:(a)CREfor the nearest-neighbor qubits;(b)χREfor the nearest-neighbor qubits;(c)CREfor Different distances r between two qubits with D=1;(d)χREfor Different distances r between two qubits with D=1. 本文研究了含有DM相互作用的一维XY模型.严格求解出了此模型的基态和关联函数,给出了它的相图,发现关联函数和量子相干性可以很好地标志出量子相变临界点的位置.量子相干性不仅仅存在于最近邻格点之间,也存在距离更远的两格点之间.发现DM相互作用会移动量子相变临界点的位置,甚至诱发无能隙螺旋相.指出了一些计算细节,这些细节在很多文献里没有得到适当的处理,本文对此做了进一步的补充和诠释. 附录A 自旋关联函数 这里引入两个新的算符, 它们满足如下代数关系: 类似地,y分量和z分量的关联可以表示为: 根据维克定理,可以对多算符连乘的平均值进行分解,变成二次形算符平均值的连乘,不难发现,对于展开形式可以表示为法夫式(Pfaffian)[38],即=pf(),其中α,β=x,y.换句话说,其可以写成2n×2n(n≡|j−i|)维反对称矩阵的行列式,即 而对于z分量, 可以发现,对于任意k,当其电子能谱ϵk总是正的时候,准粒子bk表象下基态没有元激发,即=0.此时,换句话说,不同格点i和j上的同种算符期待值为零,即于是,关联函数可以简化成n×n维Toeplitz矩阵的行列式表示: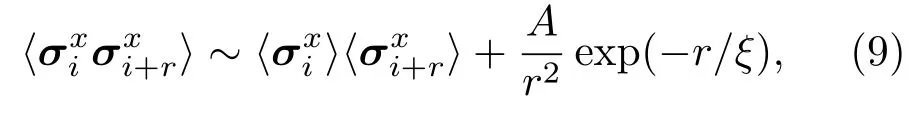


4 量子相干性
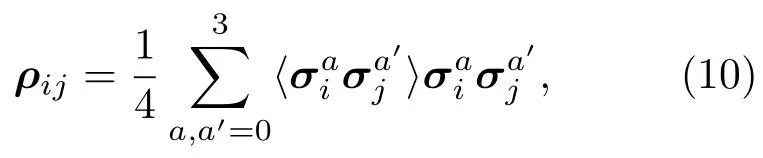
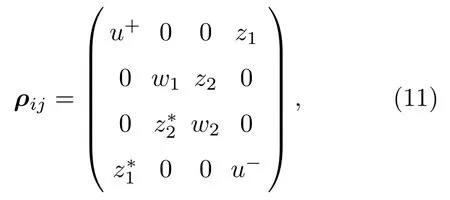
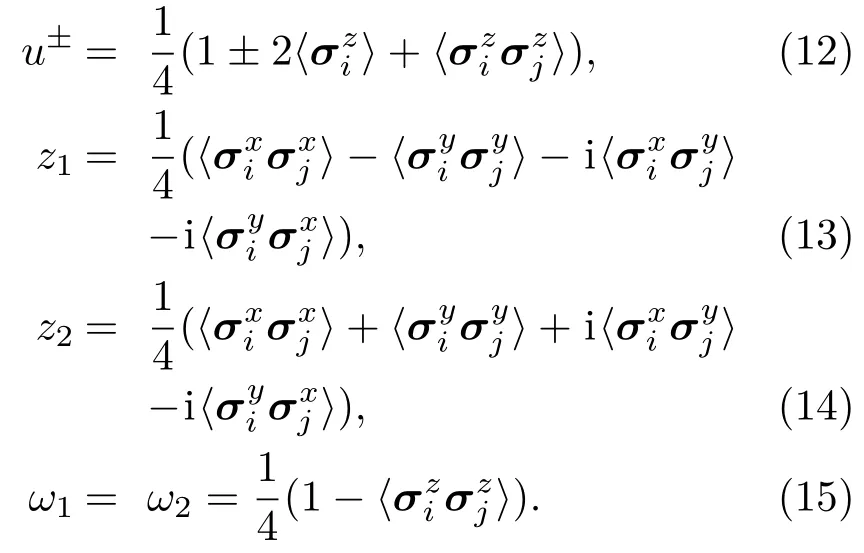



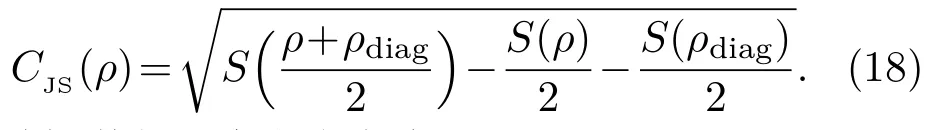
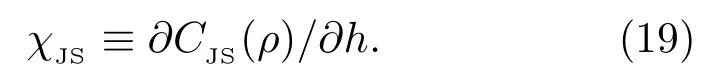
5 结 论