基于多普勒非对称空间外差光谱技术的多普勒测速仿真∗
2018-10-29况银丽方亮彭翔程欣张辉刘恩海
况银丽 方亮 彭翔 程欣 张辉 刘恩海
1)(中国科学院光电技术研究所,成都 610209)2)(中国科学院大学,北京 100049)
(2018年1月9日收到;2018年4月22日收到修改稿)
阐述了多普勒非对称空间外差光谱仪用于被动式多普勒测速的基本原理,通过综合考虑干涉条纹对比度和仪器测速灵敏度等关键因素,建立了效率函数,分别针对高斯线型和洛伦兹线型发射谱线,从理论上推导了最优单臂偏置量的选择依据,并以高斯线型目标谱线为例进行了仿真验证.同时,提出了一种基于部分干涉条纹反演多普勒速度的数据处理方法,简化了多谱线目标源的数据处理过程.结合自适应频率跟踪算法对单谱线目标源和多谱线目标源进行了仿真比较,仿真结果表明,在不考虑噪声的情况下,该方法针对多谱线目标源的多普勒测速最大绝对误差在0.004 m/s以内,与针对单谱线目标源的处理精度相当,可以满足实际应用的精度要求.
1 引 言
多普勒测速是利用多普勒效应测量目标与探测器之间的多普勒速度,就作用形式而言,可以分为主动和被动两种.主动法是指主动发射激光光源,通过测量激光回波信号的频移实现对目标物多普勒速度的测量;被动法是指无需主动发射光源,直接测量目标光源谱线的频移实现对目标源多普勒速度的测量.主动法虽然探测精度高,但是对探测条件有一定的要求,尤其在某些对仪器重量、探测距离等参量有一定限制的领域,如天文学系外行星探索,被动法成为首选.目前,国际上主要采用光栅光谱仪[1−7]、法布里-珀罗(F-P)干涉仪[8,9]、迈克耳孙干涉仪(也称傅里叶变换光谱仪,FTS)[10−12]、空间外差光谱仪(SHS)[13−16]以及多普勒非对称空间外差(DASH)光谱技术进行多普勒速度的被动式测量.DASH光谱技术是一种新型被动式干涉测量方式,由Englert等[17]于2006年首先提出.DASH光谱仪是空间外差光谱仪与迈克耳孙干涉仪的一个结合,具有两者的优点,同时具有高光谱分辨率和高灵敏度相移传感的特点,特别适合于被动式多普勒速度的高精度测量.
采用DASH光谱技术测量多普勒速度时,谱线的频移在干涉图中表现为相位的变化[18],且相位变化的灵敏度与光谱仪两臂之间引入的单臂偏置量直接相关,而单臂偏置量同时也会影响到干涉信号的对比度及信噪比.因此,单臂偏置量的合理取值是该技术中非常重要的一个环节.此外,开发出高精度的算法,由相位变化解算出目标源的多普勒速度,也是实现高精度多普勒测速的关键.
本文通过综合考虑干涉条纹对比度和仪器测速灵敏度等关键因素,建立了效率函数,从理论上分析了DASH光谱仪最优单臂偏置量的选择依据,并以高斯线型目标谱线为例进行了仿真验证.同时,针对传统数据处理方法在解算多谱线目标源的多普勒速度时需要加窗提取等限制条件,提出了一种基于部分干涉条纹反演多谱线目标源多普勒速度的数据处理方法,并结合自适应频率跟踪算法[19]进行了仿真计算.仿真结果表明该方法针对多谱线目标源可以获得很高的解算精度,相对于传统的数据处理方法,降低了对仪器光谱分辨率的要求,且大大降低了数据处理的复杂程度,有利于多普勒测速数据的实时获取.
2 DASH光谱仪的测速原理
将迈克耳孙干涉仪两臂的反射镜替换为与光轴成一定夹角的光栅,即可得到空间外差光谱仪,若两臂的光栅到分束器的距离不相等则为DASH光谱仪.DASH光谱仪既是光谱仪,也是干涉仪.利用DASH光谱仪进行多普勒速度的测量时,主要利用的是其干涉仪功能.如图1所示,经准直后的平行光束入射到分束器上,分成两路光.两支路轴上光线与光栅法线成Littrow角θ.以θ角入射到光栅上的光线中,有一波数的光经光栅衍射后原路返回,该波数就称为光栅的Littrow波数σL.某一非Littrow波数的光经两光栅衍射后,传播方向与光轴成β角(β很小).再经分束器后的两出射波前成2β夹角,形成Fizeau干涉条纹,并记录在探测器上.仪器接收到的光谱波数为σ时,Fizeau干涉条纹的空间频率kx为
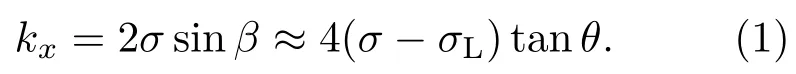
最终探测器上记录的干涉图为
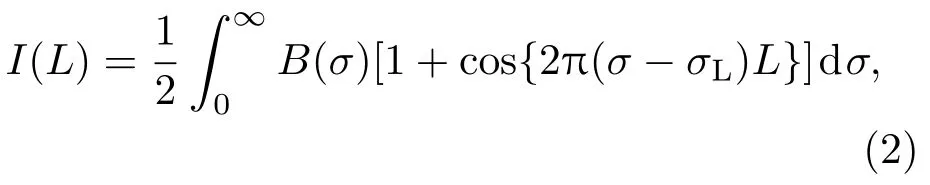
式中B(σ)为入射光谱密度;L为光程差,其计算式为

式中∆d为单臂偏置量;x为探测器上的位置(x=0表示探测器中心位置).根据文献[18],考虑目标源为有限个离散谱线情况,则x=0处对应的由多普勒频移引起的相位变化量为
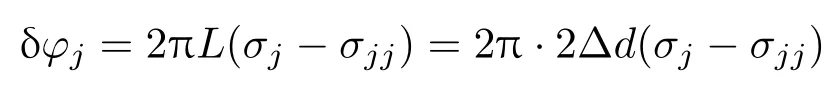

式中j表示通带内谱线的序号(j=1,2,3···);c为光速;σjj为第j条谱线对应的多普勒速度vj为0时的波数,并且探测器接收到的第j条谱线波数因此根据(4)式,就可以计算出相应的多普勒速度.

图1 DASH光谱仪原理图Fig.1.Schematic diagram of DASH spectrometer.
3 最优单臂偏置量的选择
由第2节可知,本文需要获取因谱线的多普勒频移而引入的相位变化量δφ,而光程差L越大,相位变化越明显.所以为了获得更高的探测灵敏度,光程差越大越好.但是,由于谱线线宽对相干长度的影响,干涉条纹的对比度随着光程差的增大而减小.显然,若光程差选择过大,则将导致干涉条纹对比度太小,系统的信噪比会大大降低,严重影响最终的反演精度.因此,为了优化光程差的选择,定义效率函数P为光程差L与对比度V的乘积,使P为最大值的L即为光程差的最优取值[20].再根据光程差与单臂偏置量的关系,就可以解算出最优单臂偏置量∆dopt.
干涉条纹的对比度V与谱线的线型线宽、光程差L紧密相关.常见的谱线线型主要有高斯线型、洛伦兹线型和矩形函数分布形式.其中,矩形分布函数是一种理想情况,这里不予考虑.
展开(2)式,得

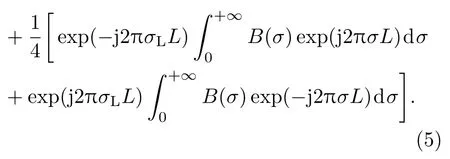
3.1 Gauss线型对应的最优单臂偏置量
高斯线型谱线的光谱密度分布可写为[21,22]
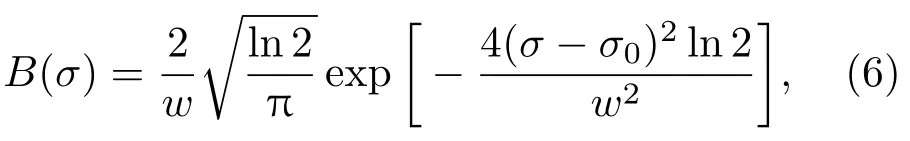
式中σ0为谱线中心波数;w为光谱密度分布的半高全宽.因此有

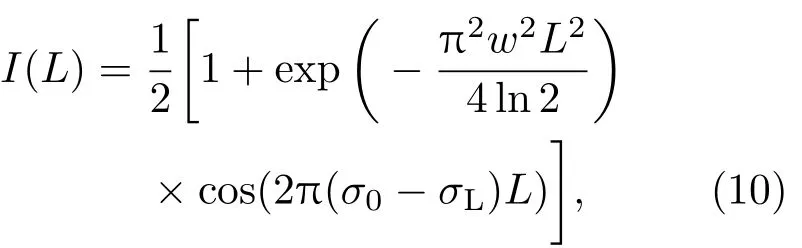
对于高斯线型的谱线,其效率函数为
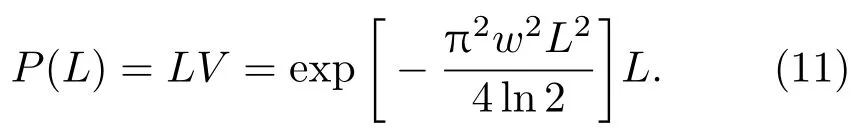
求使该效率函数取最大值的光程差L,则
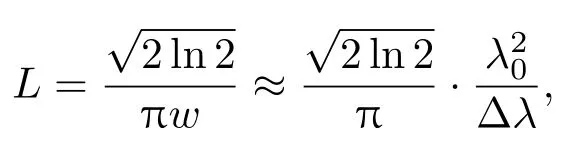
其中λ0为中心波长,∆λ为对应的波长域的半高全宽.对于x=0,可以得到高斯线型谱线对应的最佳单臂偏置量
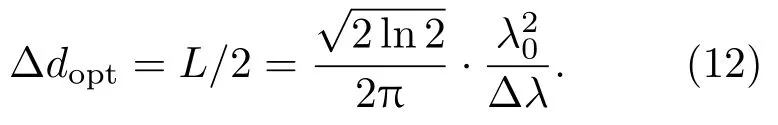
例如,对于中心波长为635.2 nm,线宽为0.005 nm的高斯线型谱线,最优单臂偏置量约为15.1 mm.
3.2 洛伦兹线型对应的最优单臂偏置量
洛伦兹线型谱线的光谱密度分布可写为[21−23]
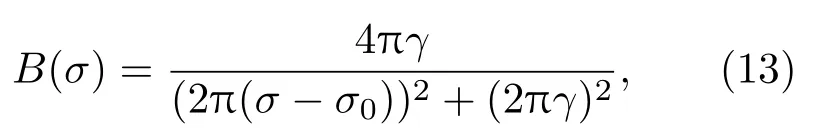
式中γ为光谱密度分布的半高半宽.因此有
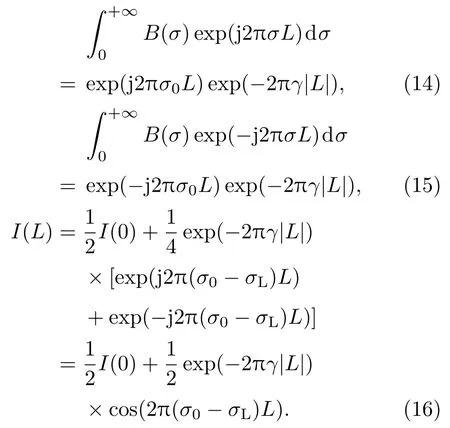
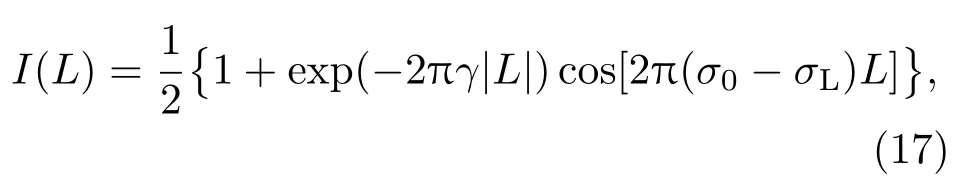
所以,对比度V=exp(−2πγ|L|).
洛伦兹线型的谱线,其效率函数为
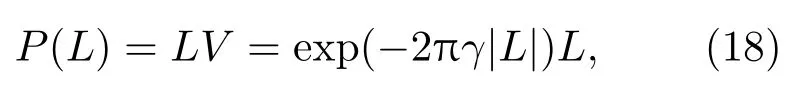
取L>0,然后求使该效率函数取最大值的光程差L,则有所以,对于x=0,可以得到洛伦兹线型谱线对应的最佳单臂偏置量
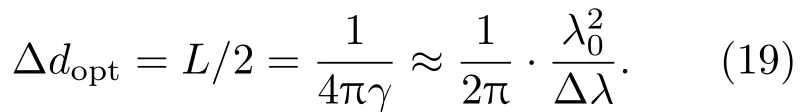
例如,对于中心波长为635.2 nm,线宽为0.005 nm的洛伦兹线型谱线,最优单臂偏置量约为12.8 mm.
4 DASH测速仿真
利用DASH光谱仪针对目标谱线进行多普勒速度测量时,可以从改良周围环境、选取最佳单臂偏置量、选择最优数据处理算法三个方面提高多普勒速度的测量精度.抛开环境的影响,单臂偏置量取最佳,是为了使DASH光谱仪的结构调整到最佳以增大相位测量灵敏度,为后端数据处理提供良好的输入;选择最优的数据处理算法,是为了在数据处理过程中能有效还原目标信号且引入最小的误差,以增加最后测量结果的可信度.下面,以高斯线型目标谱线为例,围绕单臂偏置量和数据处理算法两个方面,对DASH测速情况进行仿真.
4.1 单臂偏置量取值的仿真
假设目标源为单发射谱线,中心波长为635.2 nm,线宽为0.005 nm,线型为高斯线型,当多普勒速度v分别为0和2000 m/s时对应的谱线分布如图2所示.在不考虑噪声情况下,仿真计算了目标源发生多普勒频移时,干涉条纹对比度及干涉条纹的移动量随光程差的变化,如图3所示.其中,红线表示多普勒速度为0时对应的干涉条纹,蓝线表示多普勒速度为2000 m/s时对应的干涉条纹(因为多普勒频移量较小,红线被蓝线所覆盖).这里红、蓝线均是正弦变化曲线,只是因为条纹分布过于密集而无法观察出正弦分布,但其分布轮廓足以反映对比度随光程差的增大而逐渐减小的变化规律.图3中的绿线表示红、蓝两幅干涉图之差,可以反映目标源发生多普勒频移时,干涉条纹的移动量随光程差的变化.从图3可以看出,随着光程差的增大,多普勒频移前后干涉图差值的包络先增大后减小.显然,在包络的最大值处,相移测量的灵敏度最高,而该包络最大值对应的光程差即为最优光程差,则对应的最优单臂偏置量约为14.01 mm.该仿真结果与3.1节的理论推导结果基本一致,微小的偏差可能是仿真模拟时谱线线宽并不严格等于0.005 nm所导致的.

图2 单目标发射谱线分布图Fig.2.Distribution of single target emission line.
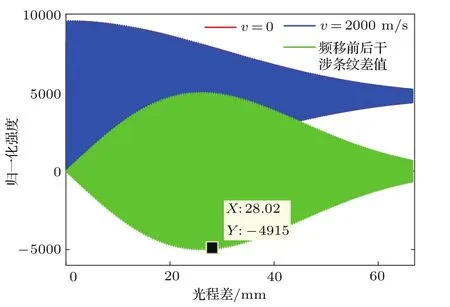
图3 目标源发生多普勒频移时,干涉条纹对比度及干涉条纹移动量随光程差的变化情况Fig.3.Variation of contrast and movement of the interference fringes with the optical path difference when the Doppler frequency shift occurs in the target source.
4.2 单发射谱线目标源反演仿真
不考虑噪声情况下,采用4.1中的目标谱线与基本参数如表1所列的DASH光谱仪,利用自适应频率跟踪算法[19],针对单发射谱线目标源进行DASH测速仿真.目标谱线经过DASH光谱仪后,得到的干涉图记录在电荷耦合元件(CCD)上,例如,多普勒速度分别为0,2000 m/s时对应的干涉图如图4所示.采用自适应频率跟踪算法分别对频移前后的干涉图进行处理,可以反演出多普勒速度.针对一系列不同多普勒速度设定值,图5给出了相应的反演结果以及绝对误差的绝对值,其中蓝色柱形图表示最终得到的反演速度值,红色曲线表示反演速度值相对于速度设定值的绝对误差的绝对值.从图5中可以看出,反演结果的绝对误差的绝对值均不大于0.0045 m/s,表明自适应频率跟踪算法针对单发射谱线目标源的多普勒频移可获得很高的解算精度.
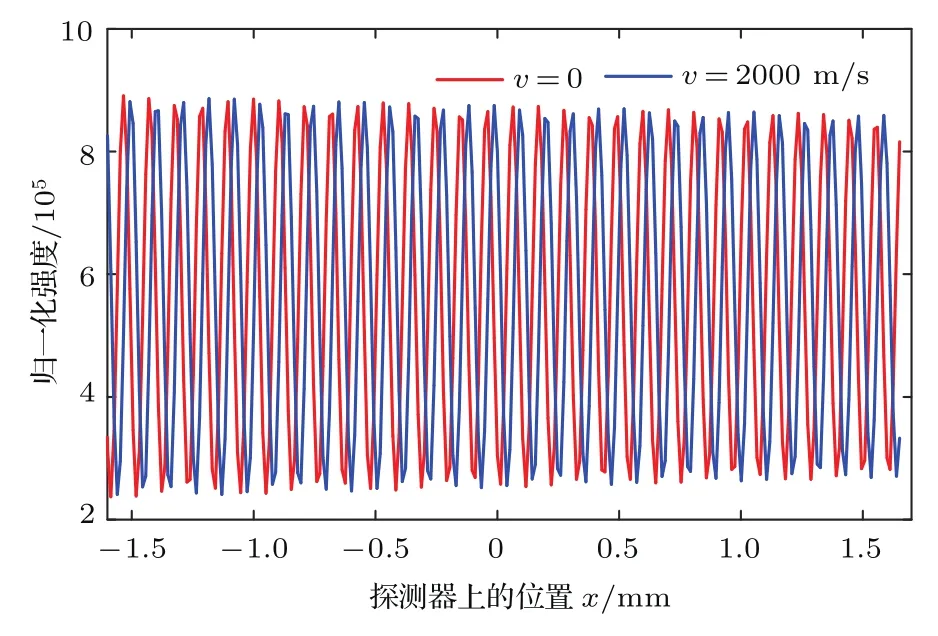
图4 单目标发射谱线干涉图Fig.4.Interferogram of single target emission line.

表1 仿真计算中DASH光谱仪的基本参数Table1.Basic parameters of DASH spectrometer in the simulation calculation.
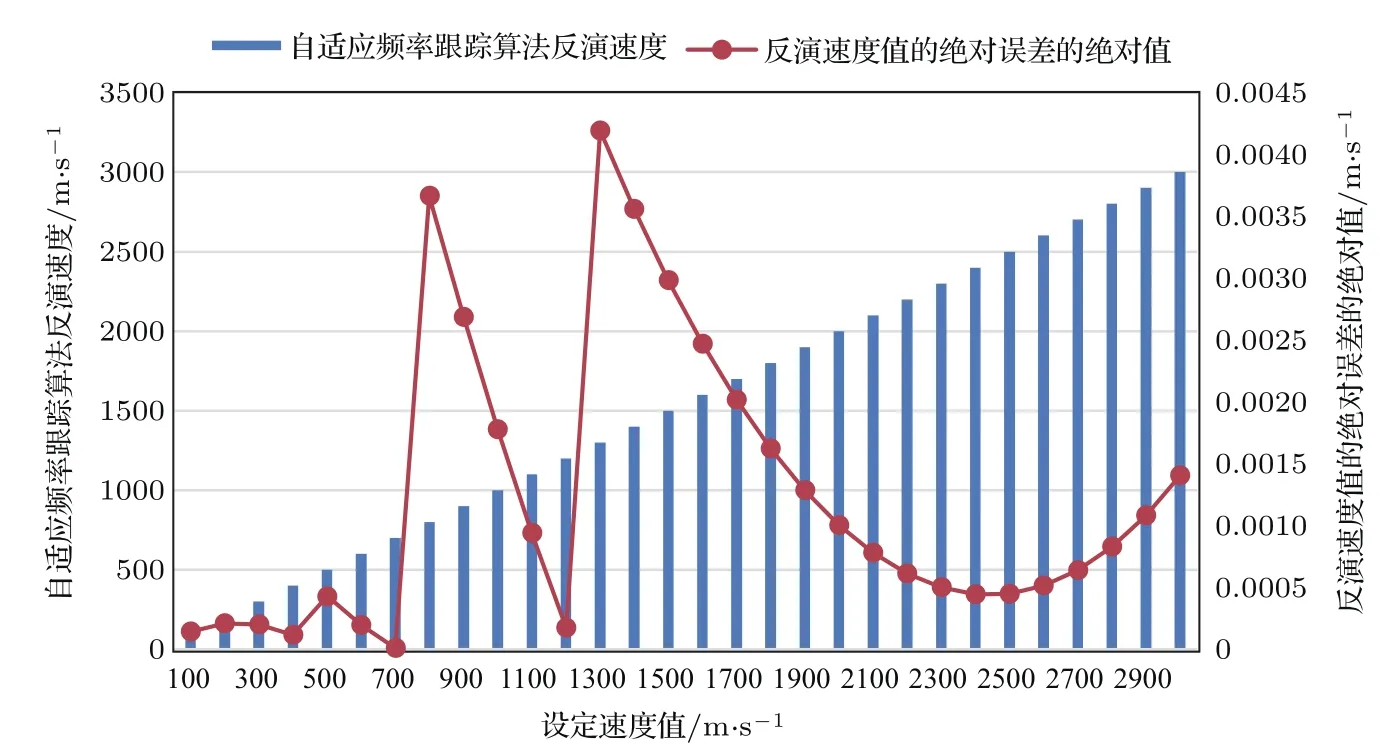
图5 单谱线目标源自适应频率跟踪算法反演结果Fig.5.Inversion results of adaptive frequency tracking algorithm for single target emission line.
4.3 多发射谱线目标源反演仿真
实际测量中有些目标源中的谱线分布比较密集,若在进行数据处理时仍需将其中的单根谱线滤出,则将对光谱仪的分辨率提出非常高的要求.与迈克耳孙干涉仪类似,DASH光谱仪的光谱分辨率与光程差采样范围变化量密切相关,光程差的采样范围越大,光谱分辨率越高.要想获得足够高的光谱分辨率,需要采用大面积光栅和探测器,并对全幅面干涉图进行采样,这将加大仪器的加工难度和数据处理的复杂程度.针对这一问题,本文提出一种只截取探测器上部分干涉图进行多普勒速度反演的处理方法,无需加窗提取单根谱线,而是将多根目标谱线等效为一个波包,利用自适应频率跟踪算法反演该等效波包相应的多普勒速度.
仍采用上述的DASH光谱仪在无噪声环境下进行针对多谱线目标源的反演仿真.假定滤波片透过谱段内有3条目标发射谱线,多普勒速度为0的情况下,中心波长分别为635.1,635.2,635.3 nm,线宽均为0.005 nm的高斯线型谱线.多普勒速度为0和2000 m/s时,探测器接收到的谱线分布以及干涉图分别如图6和图7所示.分别设定一系列不为0的多普勒速度,利用自适应频率跟踪算法对部分干涉图进行处理,反演结果如图8所示,其中蓝色柱形图表示最终得到的反演速度值,红色曲线表示反演速度值相对于速度设定值的绝对误差的绝对值.从图8可以看出,反演结果的误差非常小,最大绝对误差小于0.004 m/s.
仿真结果表明,针对目标源为相邻多条谱线情况,将多谱线目标源等效为一个波包进行处理的方法具有可行性,可获得与单谱线相当的多普勒速度解算精度.这是因为虽然对应同一多普勒速度的不同谱线具有不同的频移,但由于多根谱线分布较为密集,频率相差不大,频移量几乎相同,等效波包的频移量能反映各单根谱线的频移量,因此可以保证多普勒速度的计算精度.这种处理方法不仅降低了对光谱仪光谱分辨率的要求,还减小了数据计算量,加快了解算速度,增加了DASH光谱仪进行多普勒速度测量的实时性.
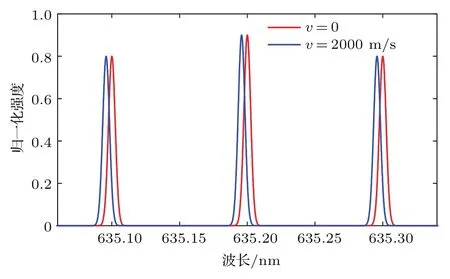
图6 多目标发射谱线分布图Fig.6.Distribution of multi-target emission lines.

图7 多目标发射谱线干涉图Fig.7.Interferogram of multi-target emission lines.

图8 多谱线目标源自适应频率跟踪算法反演结果Fig.8.Inversion results of adaptive frequency tracking algorithm for multi-target emission lines.
5 结 论
介绍了多普勒非对称空间外差(DASH)光谱技术的基本原理,推导了DASH光谱仪最优单臂偏置量的选择依据,并进行了仿真验证.同时,提出一种仅截取探测器上部分干涉图进行处理的方法,在频率域直接将多条谱线看作一个波包处理,结合自适应频率跟踪算法对多普勒测速误差进行评估.仿真结果表明该方法获得的反演速度值的最大绝对误差小于0.004 m/s,同时,该方法可以降低对光谱仪光谱分辨率的要求,减小数据计算量,从而加快解算速度.基于DASH光谱技术的多普勒测速方法具有测速精度高、光通量大、无运动部件、可多条谱线同时测量等优点,在被动式高精度多普勒测速领域具有广阔的应用前景.
