高对比度目标的电磁逆散射超分辨成像∗

范启蒙 尹成友

(国防科技大学电子对抗学院,脉冲功率激光国家重点实验室,合肥 230037)

(2018年2月2日收到;2018年3月15日收到修改稿)

提出了一种适用于高对比度目标的超分辨成像方法,通过结合对比度源反演方法与基于轨道角动量的超分辨技术,实现对高对比度目标的超分辨成像.首先采用基于轨道角动量的成像方法求解出对比度函数,将其作为对比度源反演方法的迭代初值,虽然初值结果与实际目标相差较大,但是由于初值中已经包含了关于目标的倏逝波信息,再利用这个初值开始迭代便可以得到超分辨重建结果,这种方法具有一定的抗噪声能力.本文研究表明,为了实现超分辨成像,一方面需要将目标对应的倏逝波信息转化到测量数据中,另一方面还要保证成像算法能够充分利用这些信息.本文所引申出的关于超分辨信息的概念对于逆散射超分辨成像的研究具有一定的借鉴意义.

1 引 言

逆散射模型的应用领域十分广泛,如无损探伤、地物探测、遥感、医学成像等.在逆散射问题中,利用已知的入射场照射目标区域,结合散射场数据对目标区域进行重建.逆散射属于逆问题的一种,逆问题固有的非适定性给问题求解带来了极大困难[1].传统雷达成像的一般化数学模型也属于逆问题[2],在雷达成像领域常采用反射系数描述目标,建立线性逆问题模型,最后仅能获得二维平面图像,属于定性成像范畴;而在医学成像及其他一些领域,需要掌握目标的介电常数、电导率等特性参量[3,4],属于定量成像范畴,此时需要考虑目标内部的电磁相互作用,问题模型通常由状态方程和数据方程描述,两个方程互相耦合带来的非线性给问题求解造成了更大困难.

求解非线性逆散射问题主要有两类方法,一类是将非线性问题线性化,这种模型只适用于弱散射物体,不能计算高对比度目标,传统的玻恩近似[5](Born approximation,BA)是一种典型的线性化方法,此外,玻恩迭代方法(Born iterative method,BIM)采用迭代策略进一步扩大了BA方法的适用范围[6];另一类方法是看作优化问题处理,常用的非线性优化方法有修正梯度方法[7](modified gradient method,MGM)、对比度源反演(contrast source inversion,CSI)方法[8]等.其中,CSI方法因其简洁高效得到了广泛应用并衍生出了其他相关算法[9,10].非线性方法理论上可以求解高对比度目标,但相比于线性化方法,此类方法迭代时间长,算法流程相对复杂,并且需要合理选择迭代初值,融入先验信息也比较困难.通常情况下,为了获得更好的重建效果还需要加入正则化项.最近,利用目标的稀疏先验信息结合压缩感知(compressive sensing,CS)理论的稀疏正则化方法为求解逆散射问题提供了新的思路[11,12].

分辨率是衡量重建质量的重要指标,由于电磁波的衍射特性,实际能够达到的分辨率受衍射极限的约束,如果能够突破衍射极限就是超分辨,关于突破电磁衍射极限的研究最近得到了广泛关注[13,14].为了实现超分辨,需要获取目标的倏逝波信息,这些信息可以通过近场测量得到[15,16],但这种方法对于实际逆散射问题并不现实,因此,利用远场数据实现超分辨引起了学者们广泛的研究兴趣[17−19].事实上,只要在算法中融入了倏逝波信息,即使利用远场测量数据依然能够实现超分辨[20],因此非线性方法自然地具有一定的超分辨能力.根据电磁场理论,远场只能测量传输波,而超分辨信息蕴含在倏逝波中,之所以能够利用传输波实现超分辨成像,是因为超级振荡理论[21−23]指出对于一个带限信号,在足够小的范围内可以存在任意高频的振荡,这为传输波中包含倏逝波信息提供了理论支撑.最近,轨道角动量理论[24,25](orbital angular momentum,OAM)被用于成像领域实现超分辨,但仅限于雷达成像[26,27]或者低对比度的电磁逆散射成像问题[28],对于高对比度目标的超分辨成像问题尚没有相关研究.

本文针对高对比度目标的超分辨成像问题开展研究,通过融合CSI方法与OAM超分辨技术提出了一种新的超分辨成像方法.首先利用轨道角动量衍射层析成像[28](orbital-angular-momentumdiffraction-tomography,OAM-DT)方法得到包含超分辨信息的对比度函数初值,再基于这个初值开始CSI迭代,实现了高对比度目标的超分辨成像,重建结果的分辨率要优于CSI方法的分辨率,此外还弥补了OAM-DT算法只能用于低对比度目标的不足.

2 逆散射模型

二维逆散射问题的几何模型如图1所示,D表示成像区域,由目标与背景媒质组成,整个成像区域的对比度函数未知,背景媒质可能是自由空间,也可能是其他成分.发射天线与接收天线按一定规律分布在成像区域周围的圆环Γ上,在图1中黑色实心圆既代表发射天线,又代表接收天线.人工设置激励源照射成像区域,利用接收点测量得到的散射场数据对目标区域进行重建.设电磁场的时谐因子为exp(jωt),对于线源照射或TM平面波照射的情况,电场所满足的波动方程可以表示为

其中 Ez表示z向电场,Jz表示z向电流密度,ω表示工作角频率,表示真空中的波数,µ0,ε0分别表示真空中的磁导率和介电常数.本文研究二维标量问题,为简便起见,在下文的表示中省去下标“z”.(1)式可以转化成积分方程

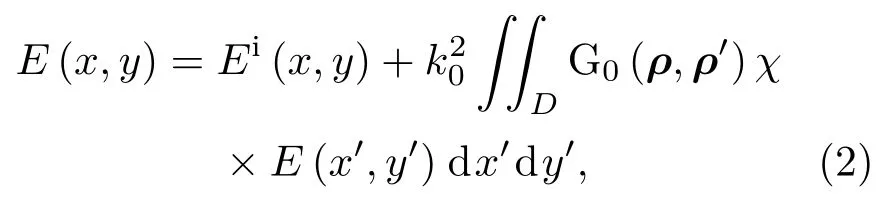
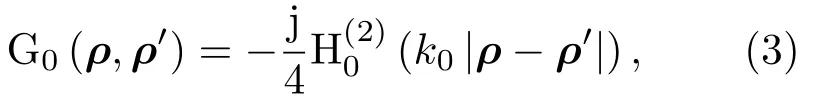
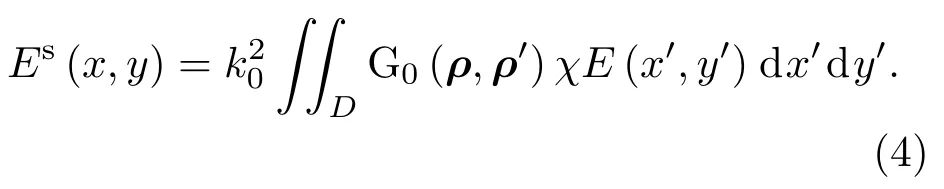
通常将(2)式与(4)式分别称作状态方程与数据方程.为了方便表述,将(2)式与(4)式写成算子形式:

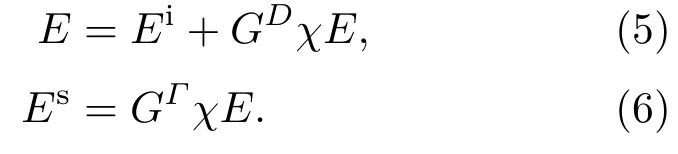
算子GD是成像域D到D的映射,算子GΓ是成像域D到测量域Γ的映射.通过观察发现,状态方程与数据方程互相耦合表现出很强的非线性,这给逆散射问题的求解带来了很大困难.

目标重建结果的分辨率与测量数据所包含的谱信息有关,对于二维问题,如果测量数据对应的两个维度的谱范围是kx∈[−kxm,kxm],ky∈[−kym,kym],则在空域两个维度上所能达到的分辨率为

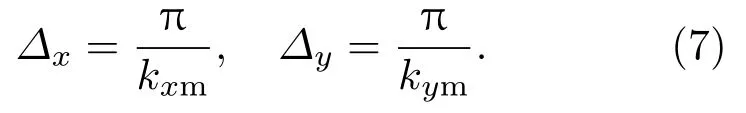
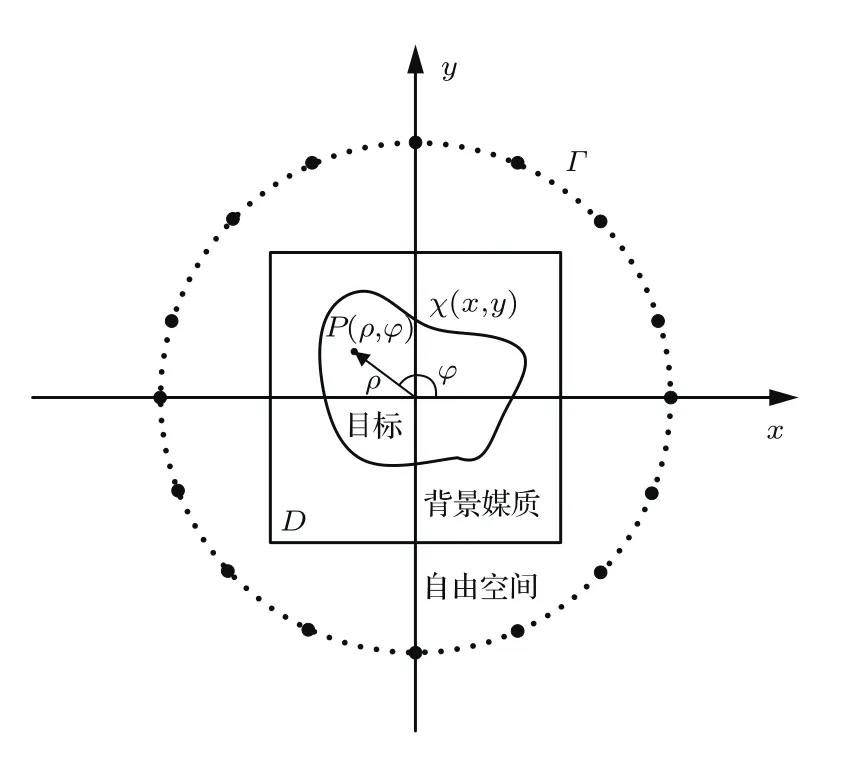
图1 二维逆散射模型Fig.1.Geometry configuration of 2-dimensional(2D)inverse scattering problem.

进行远场测量时,由于不能得到目标的倏逝波信息,测量数据的谱范围限定在[−k0,k0],对应所能达到的分辨率就是Rayleigh极限,为了实现更高的分辨率,就需要拓展测量数据的谱范围.观察(4)式发现,散射场Es是χ与格林函数G0和总场E复杂作用的结果,为了将χ更多的谱信息转化到Es中,一方面可以通过改变测量场景来修正格林函数,这就是复杂信道的超分辨机理[29];另一方面,如果在计算散射体内部总场时不做近似,就会自然地考虑目标内部或相邻目标之间的电磁相互作用,从而在算法中融入了倏逝波信息,所以非线性成像方法都具有一定的超分辨能力,或者在BA条件下通过设计入射场将倏逝波信息转化到传输波内,从而实现远场超分辨成像,基于OAM的超分辨算法便是这种思想.

3 OAM-CSI超分辨算法

利用隐含超级振荡的OAM入射场可以实现超分辨成像,但目前只应用于弱散射目标;非线性方法除了可以处理高对比度目标外,由于考虑了目标内部的相互耦合,自然地具有一定超分辨能力.下面结合CSI方法与OAM入射场,实现对高对比度目标的超分辨成像,重建结果的分辨率要优于CSI方法.

3.1 OAM电磁波的产生方法

在经典电动力学理论中,电磁波不仅携带线性动量,还携带角动量.角动量可以分为旋转角动量(spin angular momentum,SAM)和轨道角动量.在射频领域,可以采用不同的方法产生携带OAM的电磁波[30,31],但通常都是在三维场景下,本文采用均匀圆环阵产生二维OAM电磁波,如图1所示,N个线源在圆环Γ上等间距分布,令相邻线源之间的相位差为δφ=2πl/N,其中l为拓扑电荷数,一般又称作模式数,此时入射场是多个柱面波的叠加

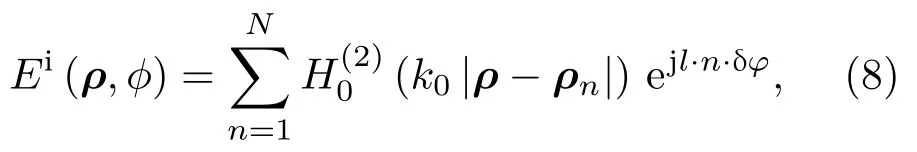
其中ϕ表示极坐标中的方位角,ρn,φn分别表示第n个线源的位置与调制相位.本文采用的均匀圆环阵由30个线源组成,圆环阵以原点为圆心,半径为3λ.图2给出了l=3,5,7时OAM电磁波的幅度分布与相位分布,可以发现 OAM电磁波的幅度分布呈现出“甜甜圈”结构,并且能量空洞随着l的增大而增大,相位分布则成周期旋转结构,与三维OAM电磁波不同的是二维情况下不存在距离扩散现象.在下面的分析中可以看到,OAM电磁波独特的场结构可以用来做超分辨入射场.

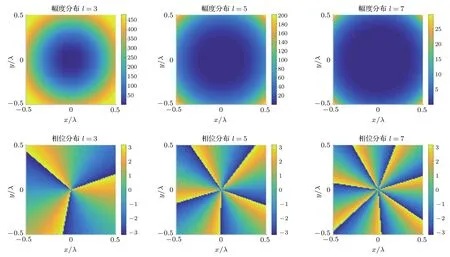
图2 l=3,5,7时的OAM电磁波的幅度分布(第一行)与相位分布(第二行)Fig.2.Distribution of amplitudes(top row)and phases(bottom row)of OAM-carrying fields.From left to right,they correspond to l=3,5,7.

3.2 高对比度目标的超分辨成像算法

文献[28]假设OAM电磁波的幅度在成像区域内均匀分布,这只是一种理想情况,实际中很难实现,并且文献[28]中基于BA的OAM-DT算法只适用于低对比度目标.为了实现对高对比度目标的超分辨成像,不妨仍然先采用OAM-DT算法的结果作为初值,此时(4)式可以写成

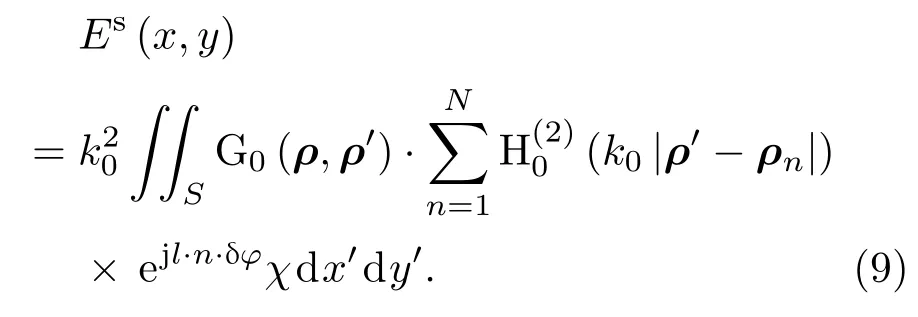
根据图2,可以将入射场近似写成Ei(ρ,ϕ)≈A(ρ)ejlφ,A(ρ)表示幅度分布,那么(9)式可以写成

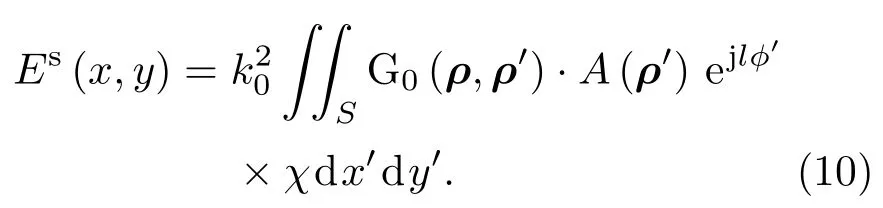
事实上,如果成像区域较小,几乎完全落在OAM电磁波的能量空洞内,则仍能够近似认为成像区域内的入射场幅度是均匀分布的,假设成像区域内入射场的幅度近似为A0,则(10)式可以近似表示为

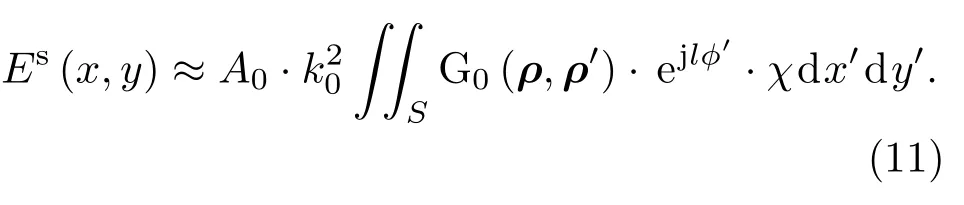
为了实现对χ的精确重建,散射场数据应包含尽可能多的χ的谱信息.定义函数f(x,y)的二维Fourier变换为

将(11)式转化到谱域考察,可以写成

“∼”为对应的谱域表示,“⊗”表示卷积运算,其中

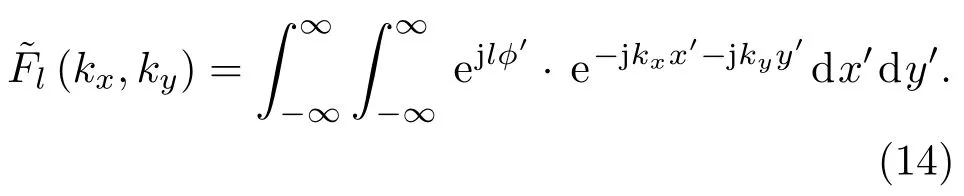
在谱域来看,散射场的谱是入射场的谱与对比度函数的谱混频的结果,假设入射场包含谱域分量kin,则远场可测量得到的目标谱信息k的范围应满足|kin−k|6 k0,对应传输波的范围,为了得到更多的关于目标的谱信息,应使kin的范围尽可能大.事实上,OAM电磁波中只有部分区域的相位面按照ejlφ分布,对应超级振荡区域,这一局部区域的空间谱范围远超过k0,而入射场总的谱范围依然小于k0.将成像区域放置于超级振荡区域便能够将对比度函数的倏逝波信息转化到散射场中,从而实现超分辨.

将(9)式离散化可以整理成矩阵形式

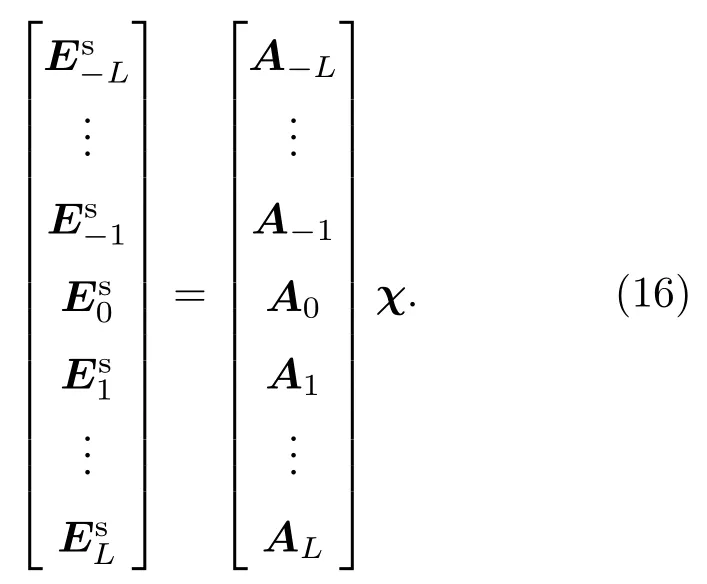
记(16)式为

采用Tikhonov正则化方法求解χ,

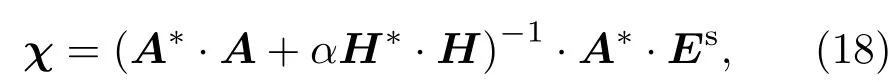
其中H表示平滑矩阵,如果χ是N×1维向量,则0阶平滑矩阵为N阶单位阵,“*”表示共轭转置,α是正则化参数,α的选取会对计算结果产生重要影响,本文通过数值实验的方法来确定.

求得对比度函数初值后,便能够按照CSI方法的流程开始迭代.CSI方法在每一次迭代过程中可以分为两个步骤,第一步通过定义对比度源w=χE,构造Es与w的线性关系,迭代更新w;第二步根据w直接求解出χ.定义对比度源后,状态方程与数据方程可以写成

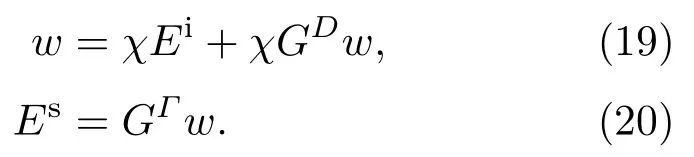
代价函数定义为归一化的状态余差和测量余差之和

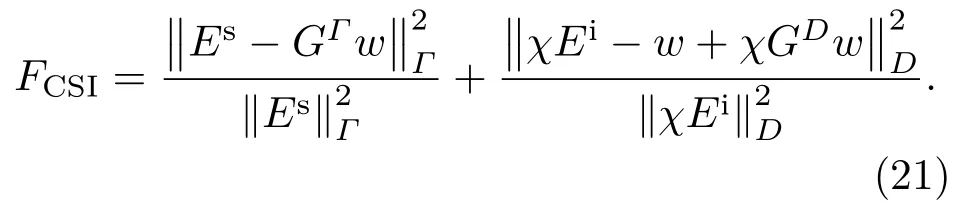
其中∥·∥Γ, ∥·∥D分别表示Hilbert空间L2(Γ),L2(D)上的范数.记第n次迭代的状态余差和测量余差分别为rn,ϕn

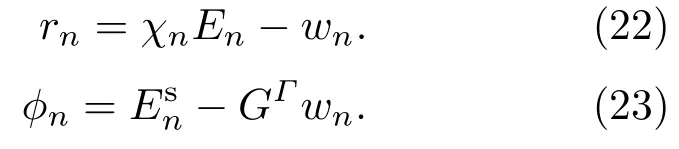
收敛指标采用归一化的散射场余差

第一步,设置对比度源初值w0;

第二步,计算散射场余差,判断Err是否小于收敛门限,如果满足收敛条件则停止迭代,否则进入第三步;

第三步,由wn,En计算χn;

第四步,由rn,φn计算wn的更新方向vn+1与更新步长αn+1并更新wn

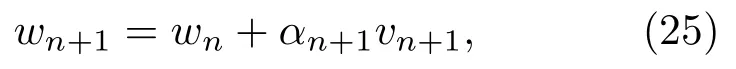
之后回到第二步.

以(18)式中的结果作为对比度函数初值,记作χ0,利用χ0可以计算得到对应的对比度源初值,记作w0,χ,接下来便可以按照上述流程开始迭代.

3.3 超分辨信息的利用

表面上看来,(18)式只是为CSI迭代确定了一个对比度函数初值χ0,事实上,由于利用了BA,OAM入射场对应的项包含在(17)式的矩阵A中,根据上文分析,真实的对比度函数χ所对应的倏逝波信息与OAM入射场做卷积,相应的信息已经包含在Es中,再利用正则化方法求解χ时,相当于用矩阵A “解卷积”,从而使倏逝波信息得以保留在初值χ0中,开始CSI迭代后,自然也利用了这些信息,所以可以实现超分辨成像.也就是说为了实现超分辨成像,不仅要能够将目标的倏逝波信息转化到测量数据中,而且在成像算法中还应该能够“真正地”利用这些信息.如果在(9)式中将对比度源w看作待求未知数,则(17)式经过离散可以得到另一种形式

在(26)式中,w表示对比度源向量,B表示对应的系数矩阵,利用相同的正则化方法可以求解出w作为CSI方法的迭代初值(称作“w初值法”),将这个初值记作w0,w.需要说明的是,w0,w与w0,χ并不相同,原因在于,通过(26)式求解w时,矩阵B只是格林函数弱形式近似的结果,并不包含OAM入射场对应的项,因此无法“解卷积”Es所含χ的倏逝波信息.也就是说,虽然Es中确实含有可以实现超分辨的倏逝波信息,但由于算法原因并未“真正地”利用这些信息.至于接下来通过CSI迭代能否实现更高分辨率的重建结果,则完全在于CSI算法本身所具有的将Es中的超分辨信息分离到χ上的能力.可以推断,w初值法的结果与直接采用CSI方法的重建结果相近.

4 计算实例与结果分析

为了验证本文方法的有效性,下面对典型目标场景进行重建,通过与CSI方法对比说明本文方法对高对比度目标的超分辨能力.在下面的计算实例中,经典的CSI方法采用后向传播(backpropagation)解作为初值:

其中GΓ∗表示GΓ的伴随算子.此外,传统的成像方法对目标照射时采用的都是序列照射法,即依次在目标周围设置照射源,其余测量点作为接收点,是“单发多收”模式,这种设置对于二维问题只能产生平面波或者柱面波对未知目标进行探测.本文采用OAM电磁波对目标进行照射,需要在目标周围设置多个照射源同时对目标照射,是“多发多收”模式.

如图3(a)所示,目标区域为λ×λ的矩形区域,区域中心与原点重合,剖分精度为λ/30.在目标区域周围以原点为圆心半径为3λ的圆环上均匀设置30个线源激励,并且在相同的位置测量散射场,OAM电磁波的照射模式l=0,±1,±2,···,±10,共有21个照射模式.此外,由于OAM电磁波照射只能提高角度分辨率,为了提高径向分辨率,可以通过移动OAM电磁波的涡旋中心来测量更多数据,在下文算例中,涡旋中心都是沿直线x=0以0.5λ的步长从y= −λ移动到y= λ.此外,仿真中所用标准散射场由CG-FFT方法求解产生.所有仿真在Dell T7810工作站上进行.

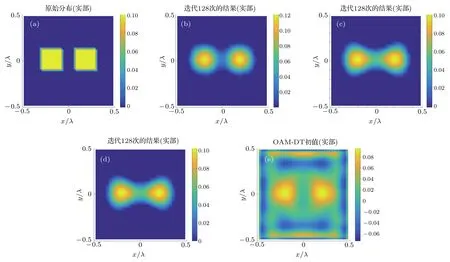
图3 双方柱重建结果,χ=0.1 (a)原始分布;(b)本文方法;(c)CSI方法;(d)w初值法;(e)OAM-DT方法Fig.3.Reconstruction of two square columns,χ=0.1:(a)Origin profile;(b)proposed method;(c)CSI method;(d)w-initial method;(e)OAM-DT method.

实例1 两个边长为λ/4的均匀方柱置于目标区域的中心,相距λ/8.首先测试低对比度目标的重建情况,两个方柱χ=0.1,工作频率设置为100 MHz.正则化参数取10−2,在CSI迭代过程中加入了对比度函数实部为正的先验信息,迭代128次结果如图3(b)所示,图3(c)是经典CSI方法迭代128次的重建结果,对于CSI方法,每次照射测量30个数据,图3(d)是w初值法迭代128次的重建结果,在本例中,三种方法继续迭代得到的结果均没有明显改善.比较图3(b)、图3(c)和图3(d)可以看出,本文所提出的方法得到的重建结果分辨率更高,并且与目标形状轮廓的符合程度要优于经典CSI方法的重建结果,而w初值法的迭代结果与CSI方法的结果几乎一致,验证了前文的推断.在图3(c)中仍然能够分辨出两个物体,这说明CSI方法作为一种非线性成像算法具有一定的超分辨能力,但相比于利用OAM电磁波照射,CSI方法提供的倏逝波信息较少.图4给出了沿y=0切面的对比度函数分布图,可以更清晰地看出本文方法成像结果的中间凹口更低,说明了其优于CSI方法的超分辨能力.可以推断,随着OAM电磁波照射模式的增加,利用本文方法可以得到分辨率更高的重建结果.文献[28]采用OAM-DT方法几乎实现了低对比度目标的完美重建,但是其采用的是理想OAM电磁波进行照射,而本文设计出了二维情形下OAM电磁波的产生结构,照射波中不仅包含相位信息,还包含幅度信息.图3(e)给出了利用OAM-DT方法求解出的初值分布,虽然成像结果不如其他方法,但是超分辨信息已经隐含在结果中,继续迭代可以得到超分辨重建结果.

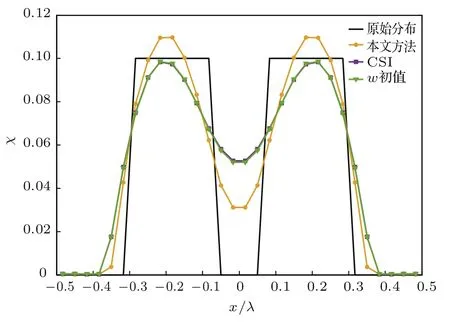
图4 沿y=0的对比度函数分布,χ=0.1Fig.4.Reconstructed contrast profiles along a central cut y=0,χ=0.1.

图5给出了本文方法与CSI方法收敛曲线的对比情况.观察发现,CSI方法对应的收敛曲线呈单调下降趋势,与w初值法的收敛曲线基本一致,而本文方法对应的收敛曲线则呈现出先上升后下降的趋势,这是由于在(18)式求χ的过程中充分利用了超分辨信息,所得到的对比度函数初值已经对应很小的散射场余差,可是考虑到逆问题的非适定性,这个很小的散射场余差对应的对比度函数可能与实际结果相差很大,但此时的对比度函数确实包含了超分辨信息.由于在CSI方法中每一步迭代都在不断更新总场,更新得到的总场幅值相对于OAM电磁波的能量空洞非常大,因此随着迭代的进行,更新得到的总场逐渐将能量空洞中的超分辨信息“淹没”,在收敛曲线上表现出仍然按照经典CSI方法的规律收敛,进而造成了收敛曲线先上升后下降的现象.本文方法与CSI方法的收敛结果相差不大,但在成像结果上有明显差别,这进一步说明了本文方法中蕴含有更多的超分辨信息.

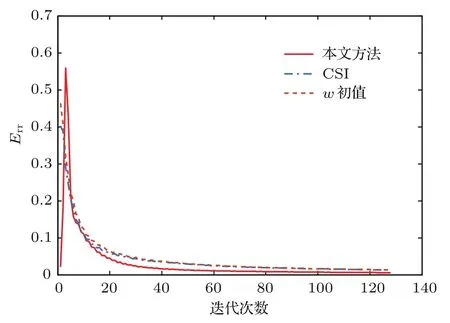
图5 收敛曲线,χ=0.1Fig.5.Convergence curves,χ=0.1.

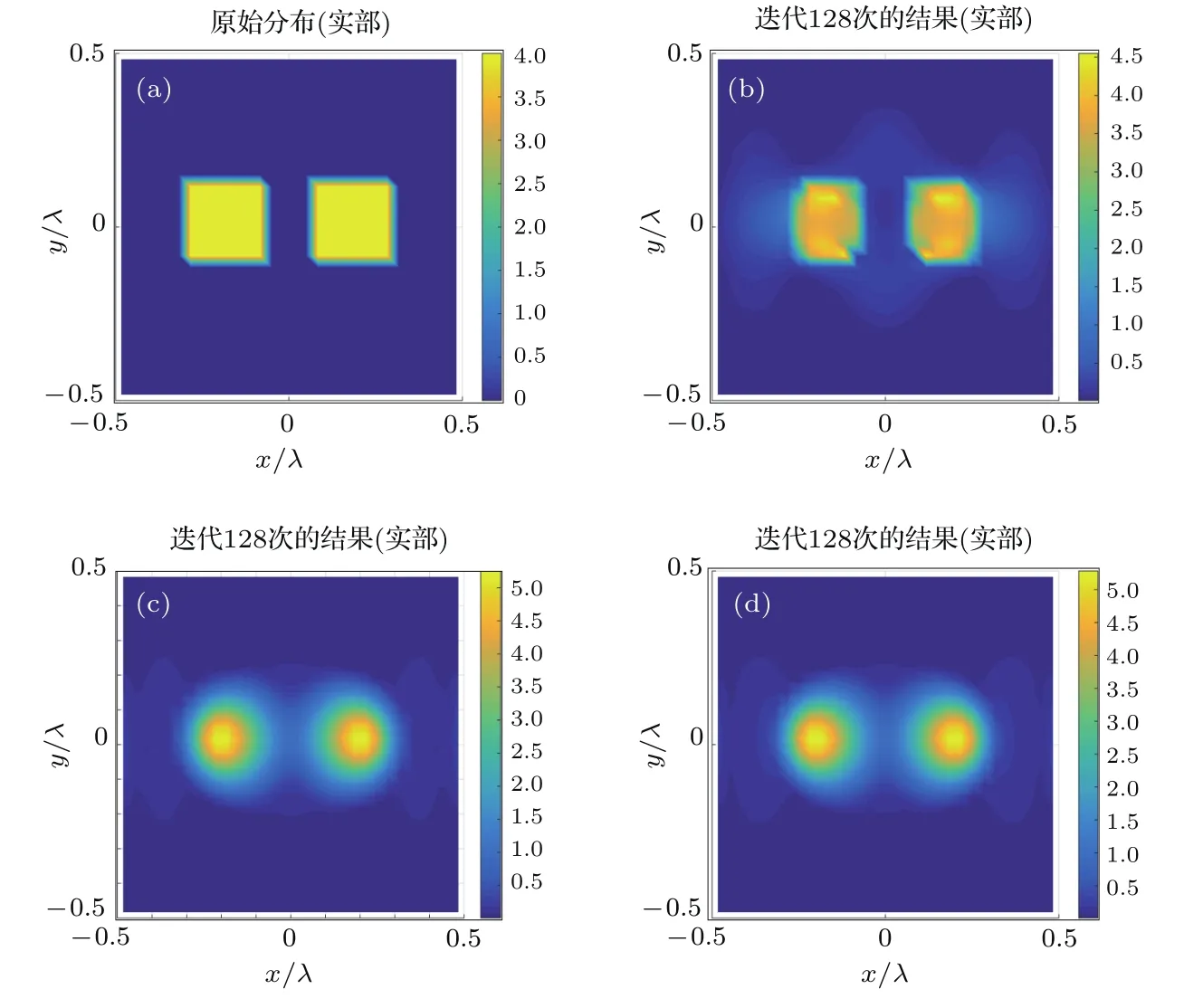
图6 双方柱重建结果,χ=4 (a)原始分布;(b)本文方法;(c)CSI方法;(d)w初值法Fig.6.Reconstruction of two square columns,χ=4:(a)Origin profile;(b)proposed method;(c)CSI method;(d)w-initial method.

实例2 令两个方柱对比度函数χ=4,其余条件与实例1相同.图6(a)是原始分布,图6(b)是本文方法迭代128次的重建结果,图6(c)是CSI方法迭代128次的重建结果,图6(d)是w初值法迭代128次的重建结果,在本例中,三种方法继续迭代得到的结果均没有明显改善.比较发现,本文方法的重建结果无论在目标轮廓成像上还是在分辨率方面都明显优于CSI方法.图7给出了沿y=0切面的对比度函数分布图,可以看出,本文方法的重建结果整体符合程度要优于CSI方法,而采用w初值法得到的迭代结果与CSI方法的结果几乎一致.

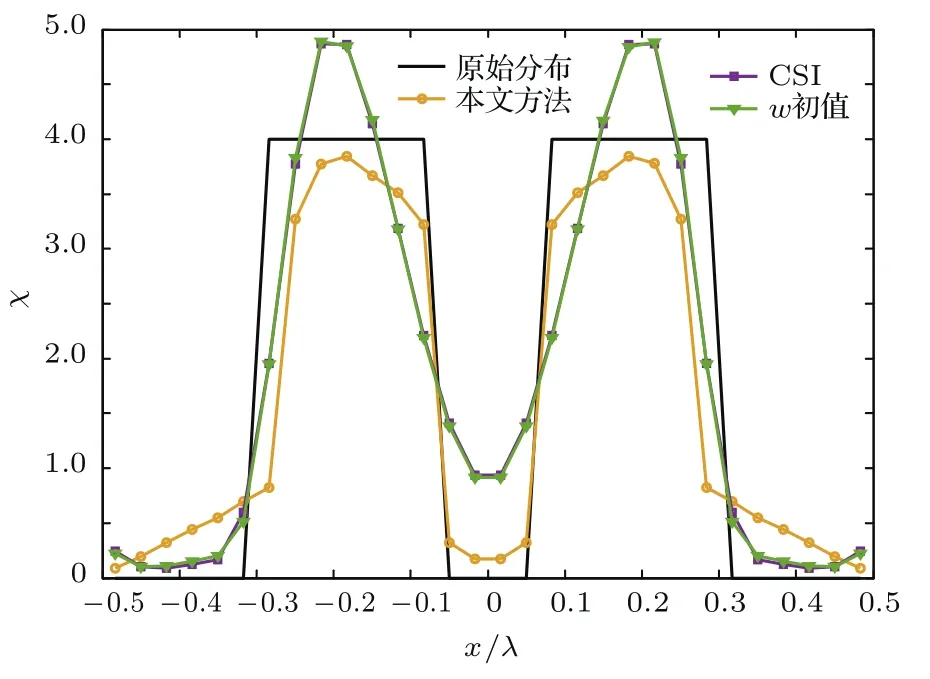
图7 沿y=0的对比度函数分布,χ=4Fig.7.Reconstructed contrast profiles along a central cut y=0,χ=4.

在图8所示的收敛曲线中,本文方法对应的收敛曲线并未像实例1中先上升后下降,这是由于对于高对比度目标一开始采用BA得到的对比度函数初值本身就具有较大误差,从图8中可以看出利用正则化方法求解得到的对比度函数初值所对应的散射场余差要远大于CSI方法迭代开始时的散射场余差,所以利用这个初值开始CSI迭代不会出现更大的余差.此外,CSI方法迭代128次后得到的散射场余差要小于本文方法对应的散射场余差,但成像结果并不如本文方法,这说明用散射场余差作为迭代收敛指标并不能准确体现整体成像性能.

图8 χ=4的收敛曲线Fig.8.Convergence curves,χ=4.

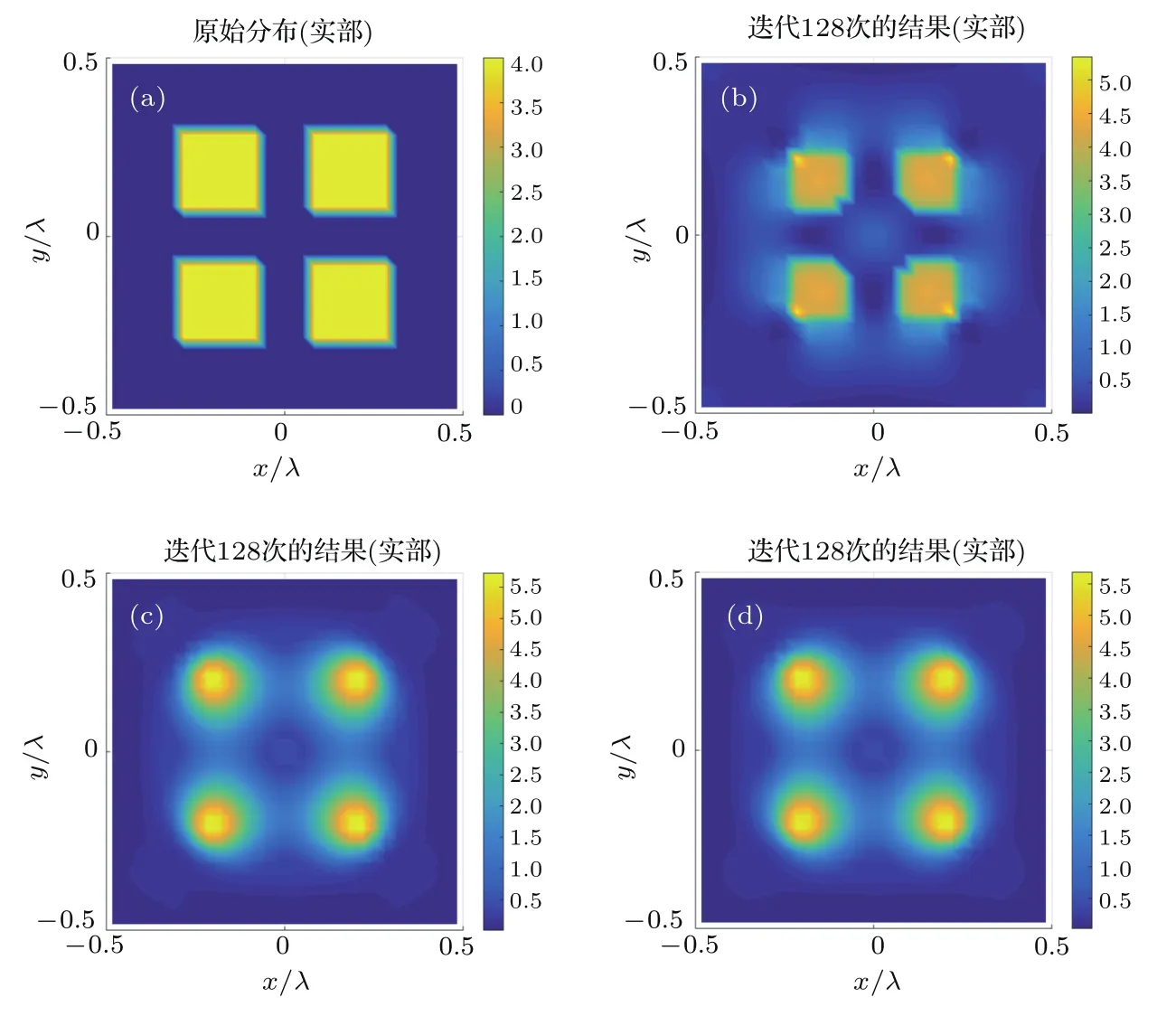
图9 4个方柱重建结果,χ=4 (a)原始分布;(b)本文方法;(c)CSI方法;(d)w初值法Fig.9.Reconstruction of four square columns,χ=4:(a)Origin profile;(b)proposed method;(c)CSI method;(d)w-initial method.

实例3 接下来增加目标场景复杂度,在成像域中部放置四个尺寸为λ/4×λ/4的小方柱,相邻方柱之间距离为λ/8,如图9(a)所示.图9(b)给出了本文重建结果,仿真设置与实例1相同,但是正则化参数选10−1,图9(c)为CSI方法重建结果,图9(d)为w初值法的迭代结果,正则化参数选取10−2,三种方法均迭代128次,继续迭代结果没有明显改善.观察对比发现,本文方法的重建结果明显优于CSI重建结果,而w初值法的迭代结果与CSI方法的结果几乎一致.这进一步说明了本文方法的有效性.

实例4 在实例2与实例3的基础上,在测量数据中加入白噪声以验证算法的鲁棒性.图10给出了双方柱在信噪比分别为20,15,10和5 dB情况下分别采用本文方法与CSI方法的重建结果,仿真设置与实例2相同.图11给出了四个方柱在信噪比分别为20,15,10和5 dB情况下采用本文方法与CSI方法的重建结果,仿真参数设置与实例3相同.从仿真结果可以看出,无论对于简单场景(双方柱)还是复杂场景(四个方柱),在不同程度的噪声影响下本文方法依然可以得到较好的成像结果,而且整体成像效果优于CSI方法,说明了本文方法具有一定的鲁棒性.

图10 不同信噪比下采用本文方法(a)—(d)与CSI方法(e)—(h)的双方柱重建结果,χ=4Fig.10.Reconstruction of two square columns with proposed method(a)–(d)and CSI method(e)–(h)corrupted by Different SNR,χ=4.

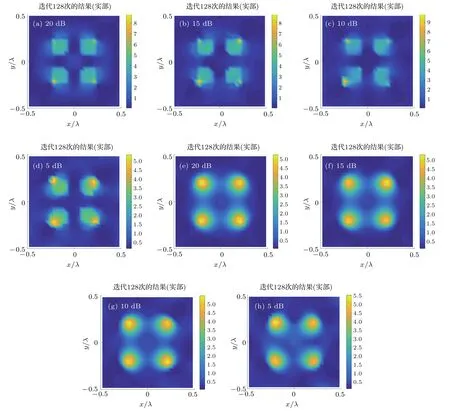
图11 信噪比为20,15,10和5 dB时采用本文方法 (a)—(d)与CSI方法(e)—(h)的四方柱重建结果,χ=4Fig.11.Reconstruction of four square columns with proposed method(a)–(d)and CSI method(e)–(h)corrupted by Different SNR,χ=4.

5 结 论

结合CSI方法与OAM-DT方法,提出了一种能够对高对比度目标实现超分辨的成像方法.首先利用OAM-DT方法求解对比度函数初值,得到的对比度函数初值包含有超分辨信息,再基于这个初值进行CSI迭代.从仿真结果来看,本文方法在目标轮廓成像和分辨率两个方面均要优于CSI方法,原因是OAM电磁波照射激发出了目标更多的谱信息,并且这些谱信息在CSI迭代过程中得以保留.此外,本文方法还具有较好的抗噪性能.本文研究表明,对于最后成像结果起重要影响的是在算法中能否融合超分辨信息,并且在算法过程中保持这些信息.本文所引申出的超分辨信息的概念,对于逆散射超分辨成像的研究具有一定的借鉴意义.