基于单一分光棱镜干涉仪的双通路定量相位显微术∗

孙腾飞 卢鹏 卓壮 张文浩 卢景琦†

1)(山东大学信息科学与工程学院,山东省激光技术与应用重点实验室,济南 250100)2)(山东大学物理学院,济南 250100)

(2017年12月22日收到;2018年4月9日收到修改稿)

仅仅使用一个单独的分光棱镜(BS),实现了一种用于生物细胞三维成像的双通路定量相位显微术.不同于传统的使用方法,将BS倾斜放置,使中央半反射层与入射光光轴之间存在一个非常小的角度.这样基于BS的分光特性,经过BS后的透射光束和反射光束将会叠加在一起并形成干涉.调节样品位置,利用相机拍摄同时获得了存在π相移的双通路干涉图.这种离轴干涉模式,只需要记录单幅干涉图就可以获得真实的相位信息,方法结构简单,易于操作,适用于微小透明样品的三维形貌测量.

1 引 言

近年来,用于识别检测透明微结构特征的技术愈发重要.相较于传统光学显微技术,定量相位显微术通过测量相位信息来间接地反映三维轮廓信息,这种技术无需对细胞进行标记即可观察完整细胞的形态和光学性质,作为一种无损伤、非接触式的光学测量技术,其已经被广泛地应用于微结构(细胞等)的形态特征测量中[1−6].常见的马赫尔-曾德干涉仪结构经常在定量相位显微术中使用,然而这种结构极易受到外部环境的干扰,最终会降低测量的精度.为解决上述问题,采用信号光束和参考光束共光路的结构[7−14]是一种不错的选择.除此之外,采用尽可能少的光学元件不仅可以实现信号光束和参考光束共光路结构以提高系统的稳定性,而且显著地简化了系统的结构以及降低了系统的成本,目前对于这一方面的研究已取得了一定成果[15−21].例如,Anand等[15]及冯少彤等[16]分别描述了仅仅使用普通平面反射镜——Lloyd镜的自参考共光路数字全息显微技术,即利用反射镜将光束的一部分反射与另一部分光束叠加形成干涉条纹;此外,Anand等[17]仅仅使用一片玻璃平板实现了横向剪切干涉显微术,获取了微小生物样品的三维轮廓信息;Yaqoob等[18]则使用两片方形平面反射镜实现了活细胞的光学色散相位测量;Qu等[19],Gabai和Shaked[20]及冯国英等[21]使用单一的分光棱镜(BS)实现了微结构的干涉相位测量.本文仅仅通过使用一个BS,提出了一种新的双通路定量相位显微术.利用这种方法,获得了较高质量的干涉图样,并成功实现了生物细胞的相位信息测量.

2 实验原理

2.1 相位提取方法

基于本文实验所采用的离轴干涉结构,只需要采集一幅干涉图就可获取样品的相位信息,故此选择应用广泛的快速傅里叶变换(FFT)法来恢复样品相位信息.FFT法[22]的具体流程参见图1.

图1 FFT法处理干涉图流程Fig.1.Flow diagram of FFT method for processing interferogram.

假设信号光波O(x,y)和参考光波R(x,y)均为平面光波,干涉条纹的光强分布可表示为

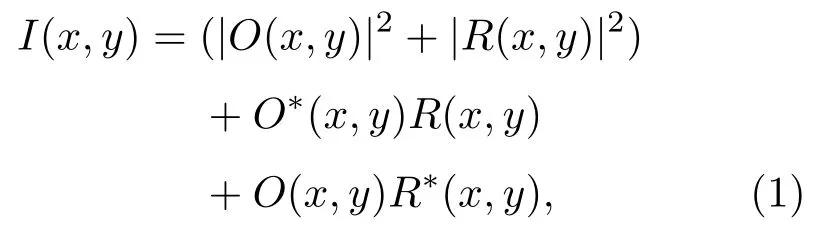
式中令O(x,y)=A(x,y)cos[φ0+φ(x,y)],R(x,y)=A(x,y)cosφ0.设A(x,y)和φ(x,y)分别为光波的振幅和样品相位分布,φ0为初始相位,“*”代表共轭.对(1)式进行FFT,然后用合适的滤波器提取出+1级频谱:

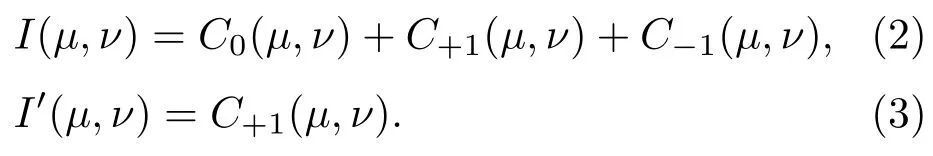
坐标(µ,ν)为与空域坐标(x,y)相对应的频域坐标.(2)式与(1)式中各项对应,分别为背景(0级)、实像(+1级)和共轭像(−1级).滤波后将+1级频谱移至谱域中心,然后对(3)式进行逆FFT得到c(x,y).利用反正切计算,从c(x,y)求解相位信息:

式中“Im”和“Re”分别代表复函数的虚部和实部.

利用求解反正切的方法来获取相位信息时,提取的相位值被限制在[−π,π],即得到的是相位被“包裹”的图像.需要对其进行相位解包裹以便得到真实的连续相位分布

式中U[]为解包裹计算,下标“u”和“w”分别代表解包裹和包裹,k为整数.

2.2 BS干涉原理

利用BS将一束光分成两束.不同于文献[19,20]中的用法,调节光束的入射位置,使其仅仅入射到BS的左(右)半部分(中央半反射层一侧),平行光束入射到BS时的光线追迹如图2所示.将一个分光比为5:5的普通BS倾斜放置,在最初状态使BS的中央半反射层与平行入射光束光轴方向平行.以BS的中央半反射层所处方向为基准,定义θ为平行入射光束光轴与BS中央半反射层之间的夹角,按照几何光学中的符号规则(以锐角度量,顺时针转为正,逆时针转为负)来表示入射光的入射状态.假设BS位置不变,当入射光束方向发生变化时,出射光束(经中央半反射层的透射光束和反射光束)的方向也随之发生变化.当θ=0时,两出射光束平行;当θ>0时,两出射光束汇聚;当θ<0时,两出射光束发散.可以很容易发现,当处于θ>0的情况下(图2(b)),经过BS之后的两出射光束(两出射光束之间存在夹角2θ)将相遇叠加在一起并发生离轴干涉.本文实验即利用这一性质.

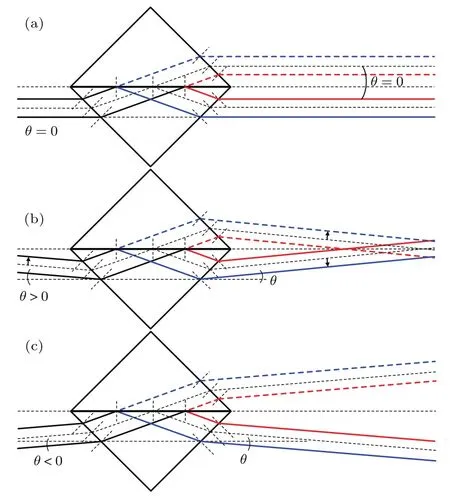
图2 平行光束以不同方向入射到BS时的光线追迹(a)θ=0;(b)θ>0;(c)θ<0Fig.2.Ray tracing of parallel beam incident to BS with Different directions:(a)θ=0;(b)θ>0;(c)θ<0.

本文提出的定量相位显微术有几个有利条件:第一,使用单一的BS可以简化光学系统,降低光学系统的成本及调节难度;第二,调节入射光束距离BS中央半反射层尽可能远,这样两出射光束之间的距离越近,这种自参考近共光路模式使得系统的抗干扰能力较好;第三,如图2(b)所示,通过调节样品的位置,使样品尽可能只占据入射光束的一半位置,这样经过BS的两出射光束就是入射光束的复制像,并且彼此相反.因此,当这两出射光束相互叠加时,其对应位置彼此干涉,形成双通路干涉形式;第四,两干涉光束之间存在一个非常小的夹角,这就形成了离轴干涉,并且干涉光束之间的夹角可以自由地调节,从而实现频谱中实像和共轭像完全分离,因此只需要记录一幅干涉图并且可以很好地提取出样品的相位信息.对于文献[19,20]中的方法,需要尽可能调节BS中央半反射层与入射光光轴共面,使得每一干涉通路中参考光束和信号光束的截面积相近,以期获得大的干涉区域.而本文方法只需使入射光束入射到BS中央半反射层的一侧即可实现同样目标,这一调节相对简单.此外,本文方法利用的是通过BS后两束光束的汇聚性质(图2(b)),而文献[20]利用了通过BS后两束光束的发散性质(图2(c)),比较两种方法,可以较容易地发现在获取同样的双通路干涉图样时,本文方法只需要更小的探测器面积.

3 实验系统及测量结果

3.1 实验装置及细节

本文提出的双通路定量相位显微术实验光路如图3所示.首先,按照传统倒置型显微镜配置搭建了光路的基础部分.使用He-Ne激光(波长λ为632.8 nm)作为照明光源,采用英国Andor公司的Zyla 5.5科研型CMOS相机拍摄干涉图,像素尺寸∆x为6.5µm×6.5µm,最大有效像素数为2560 pixel×2160 pixel(5.5 M像素).图3左侧插图显示了样品放置情况,右侧插图为双通路离轴干涉示意图,其中O(O′)代表信号光束,R(R′)代表参考光束.

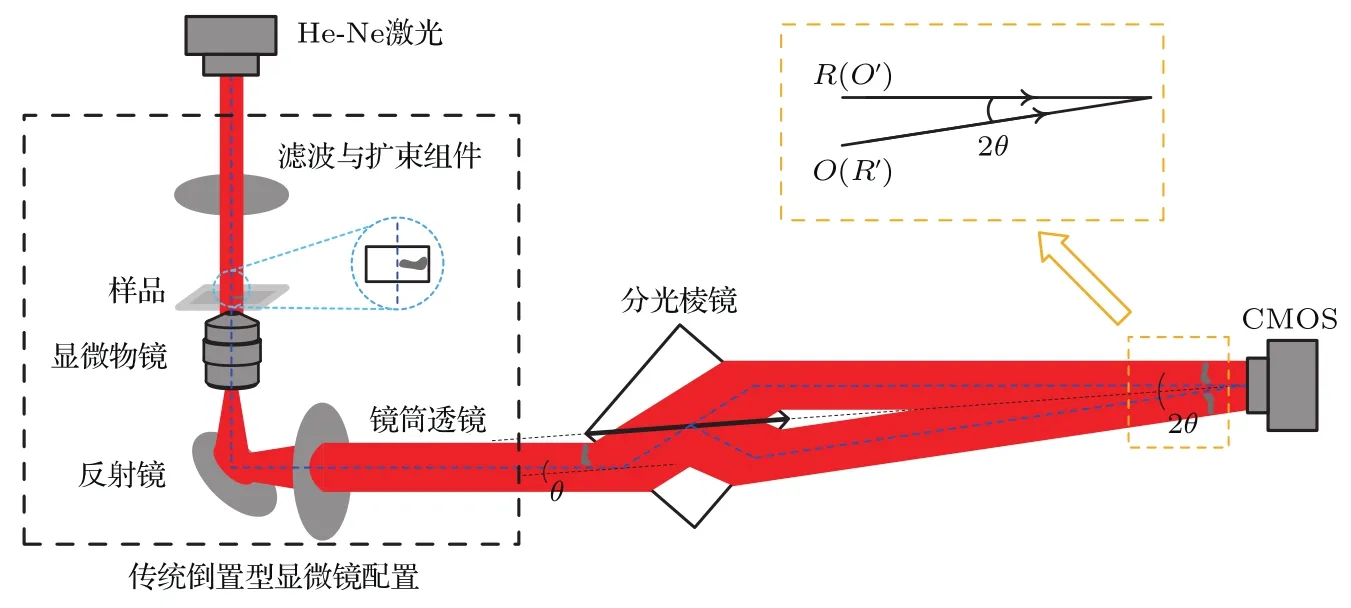
图3 双通路定量相位显微术实验光路示意图Fig.3.Experimental optical path diagram of dual-channel quantitative phase microscopy.

将BS安装在旋转台上,精细调节入射光束光轴与BS中央半反射层之间的夹角θ(根据几何关系,可以得到两干涉光束之间存在夹角为2θ),以便获取条纹对比度高的高质量干涉图.通过调节夹角θ的大小,发现干涉条纹的空间频率也随之发生变化.随着夹角θ逐渐增大,干涉图条纹变得越来越细密,干涉条纹的空间频率逐渐增大,如图4(a)所示.对应于图4(a)中不同夹角下记录的干涉条纹,计算了相应的傅里叶频谱,如图4(b)所示.从傅里叶频谱图中可以清晰地发现,随着夹角θ逐渐增大,背景(0级)频谱、实像(+1级)频谱和共轭像(−1级)频谱之间彼此远离.基于此,可以适当增大夹角θ,实现频谱中实像(+1级)和共轭像(−1级)彻底分开.这使得在滤出实像(+1级)频谱时更容易,最终只需记录单幅干涉图来重构相位,显著降低系统的复杂程度.需要注意的是必须调节夹角θ,使其满足2θ 6 sin−1(λ/2∆x),以便于满足探测器的采样条件[23].在本文实验中,应满足2θ 6 2.8◦.

由于BS产生的透射光束和反射光束均为入射光束的复制像,参考光束和信号光束均来自同一入射光束,所以这种方法实质上是一种共光束自干涉系统.对测试样品而言,希望被测试的样品中细胞稀疏分布,仅仅包含几个细胞就可满足需要.为了更好地实现双通路成像,在调节样品时,需要注意样品的位置,尽可能使样品只接触照明光束的一半.透射光束中携带样品信息的部分和反射光束中未携带样品信息的部分分别作为信号光束和参考光束形成干涉,反之亦然,这样就形成了双通路干涉模式.最后,只使用一台CMOS相机就可单次拍摄到双通路离轴干涉图.

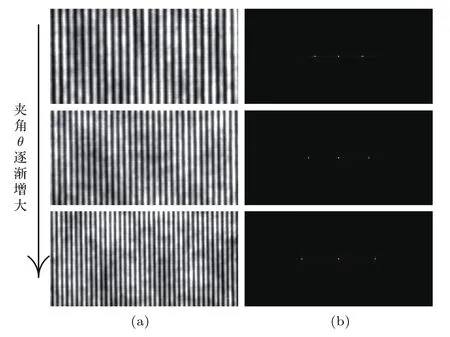
图4 夹角θ逐渐增大时干涉条纹的变化 (a)记录的干涉条纹;(b)对应于(a)的傅里叶频谱Fig.4.Variation of interference fringes with increasing angle θ:(a)Recorded interference fringes;(b)Fourier spectra corresponding to(a).

3.2 实验结果

利用草履虫样品来验证上述方法的可行性.考虑到草履虫的实际大小(通常为180—280µm),选用一个数值孔径为0.12,放大倍数为5倍的显微物镜来放大样品.拍摄的干涉图如图5(a)所示,图5(b)和图5(c)分别显示了图5(a)中方框标记部分的放大图像.干涉图的傅里叶频谱分布如图5(d)所示,用方框标记出了+1级频谱.图5(e)和图5(f)分别为图5(b)对应的二维解包裹相位图及三维相位分布,图5(g)为图5(c)对应的二维解包裹相位图.

从图5可以观察到双通路干涉情况.图5(b)两通路完全分离,而图5(c)显示两干涉通路有重叠.从图5(b)和图5(c)可知,草履虫的形状清晰可见,干涉条纹的弯曲情况非常清晰并且方向相反,这揭示出两干涉通路之间存在π相移.图5(d)频谱图中0级、+1级和−1级频谱彻底的分离,这说明本文方法可以很好地提取出实像.图5(e)—图5(g)再次清楚地显示出两通路、π相移和草履虫的形貌.图5(g)显示双通路重叠部分影响了相位信息的提取,这提醒在实验调节时要注意样品位置.重要的是,基于双通路干涉图的π相移镜像特性,可以对重构的样品相位信息进行校正,实现定量分析.由于BS的对称结构,两个干涉通路也是彼此对称的,则一个干涉通路中的相位最大值对应另一干涉通路中的相位最小值.以不同干涉通路中相位最大值和最小值的对应坐标为基准,两通路的对应相位值相减后取平均值,该平均值即为所需的精确相位值(图5(h)).图5(h)中红色和蓝色曲线分别显示了图5(e)中左侧和右侧白色虚线标记的竖直方向(分别包含了相位最大值和最小值)的相位分布,黑色曲线表示两干涉通路的平均相位分布.可以看出,双干涉通路可获得更多的相位信息,样品相位信息得到了较好的校正并且一定程度上降低了背景影响,这反映了本文方法的较好特性.综上所述,利用本文方法成功实现了透明微小样品的相位测量,揭示了样品的三维形貌,证明了本文双通路定量相位显微术的可行性.

图5 双通路定量相位显微术实验结果 (a)干涉图;(b)和(c)分别为(a)中方框标记部分的放大图;(d)傅里叶频谱图,红色方框标记了+1级频谱;(e)和(f)分别对应(b)的二维解包裹相位图及三维相位分布;(g)对应(c)的二维解包裹相位图;(h)对应(e)中白色虚线标记的竖直方向的相位轮廓分布曲线Fig.5.Experimental results:(a)Interferogram;(b)and(c)are the enlarged images of parts of the interferogram marked by box in(a);(d)Fourier spectrum,the+1 order spectrum marked with the red box;(e)and(f)are the 2D and 3D unwrapped phase maps corresponding to(b),respectively;(g)2D unwrapped phase map corresponding to(c);(h)Different vertical direction phase profile curves of cross-section at the location marked by the white dashed lines shown in(e),respectively.

4 结 论

利用BS的分光特性,通过调节BS中央半反射层和入射光束光轴之间的夹角,实现了一种双通路定量相位显微术,并通过测量微小透明样品的相位信息对实验方法进行了验证.实验结果表明,本文方法具有双通路干涉特性,两通路均能够成功地获取样品的相位信息.本文方法只需要一个单独的BS,显著地降低了系统的复杂程度,降低了成本并提高了系统稳定性,容易操作,拓展了使用范围.在将来的发展中,考虑将光源、显微物镜、BS和相机集成开发,形成一种便携式易于现场测量的定量相位显微装置.