交易制度变动对股指期货日内模式的影响

许桐桐，王苏生，彭 珂，余 臻

(1.哈尔滨工业大学 深圳研究生院，广东 深圳 518055； 2.前海金融控股有限公司博士后创新实践基地，广东 深圳 518052； 3.中山大学 岭南(大学)学院，广东 深圳 518052)

一、引 言

随着计算机技术的发展，先进算法、软件等在交易系统中的部署和应用使得交易所处理数据的速度大大提高；而通信技术的发明，改变了信息传播的媒介，加快了信息的传播速度，使得市场中的参与者通过网络形成互联，大大提高了交易的效率。信息传播速度的加快和数据频率的提高，使得研究领域逐渐由市场宏观拓展到市场微观层面。

微观结构特征变量的日内效应和微观结构变量之间的相互关系一直是市场微观结构的重点研究内容。日内效应通常指结构变量在日内的交易中呈现出的有规律的特征，微观结构变量关系主要指结构变量之间信息的传播机制和过程。国外学者对股票和期货市场的日内微观结构进行了广泛的研究，加深了人们对相关市场的了解。国内学者对A股市场和沪深300股指期货市场也进行了大量的实证分析，但对新推出的股指期货的相关研究还较少。

上证50股指期货是继沪深300股指期货推出后，我国推出的第二批股指期货。然而，在其推出后不久，我国股市就出现了大幅下跌行情。为了维护市场稳定，抑制期货市场的过度投机行为，中金所先后出台多项政策来限制股指期货的交易活动，特别是在2015年9月2日当天，中金所陆续公布了一系列的严格管控措施：将股指期货非套期保值的持仓保证金提高至40%；平仓手续费提高至0.23%；单个产品单日开仓交易量超过10手认定为异常交易行为。以上措施中以限仓政策的条件最为苛刻，其后的股指期货交易量出现了显著下降。另外，为了与现货股票市场同步，并配合股票市场熔断机制的实施，2016年1月1日，中金所将股指期货的交易时间由原先的9:15—11:30(第一节)和13:00—15:15(第二节)调整到9:30—11:30(第一节)和13:00—15:00(第二节)，明显缩短了股指期货的交易时间。

考虑到上证50股指期货上市时间较晚，其日内微观结构还有待分析，多次重大交易政策的变动可能会使市场微观结构和信息传播出现较大改变，因此，本文重点研究上证50股指期货这一新期货品种的日内微观结构，并探究股指期货交易制度变动对日内微观结构的影响。

二、文献回顾

(一)微观结构变量日内效应

国外学者对收益率、交易量、波动率和价差等微观结构变量的日内效应进行了广泛研究。如在早期的研究中，Harris(1986)[1]发现美股收益率呈现U型的日内走势，Ekman(1992)[2]发现S&P 500指数期货的绝对收益率和交易量大体呈现U型的日内效应。近年来，关于日内效应的研究仍是层出不穷。如在日本市场的研究中，Andersen等(2000)[3]发现日本股票市场的日内绝对收益率呈现UU型；Tsuchida等(2016)[4]研究日本国债期货的微观变量，发现交易量和绝对收益率呈现W型日内特征。在美国市场的研究中，Tannous等(2013)[5]分析纽交所上市股票的日内效应，发现交易量呈U型，价差呈L型；Upson等(2017)[6]进一步分析了市场报价竞争和算法交易对纽交所上市股票日内特征的影响，结果发现买卖价差的日内效应由U型变为S型，交易量的日内效应依然维持U型。另外，欧洲市场的研究也较多，如Zwergel等(2014)[7]研究德国期货市场，发现波动率呈现W型，交易量呈现横卧J型；Uctum等(2017)[8]研究四家法国公司5分钟平均绝对收益率，发现日内效应呈现U型特征；Sita(2017)[9]研究英国脱欧公投事件对FTSE100日内波动模式的影响，结果发现日内波动加剧，但是波动率U型的日内效应未改变。

国内学者对日内微观结构也进行了大量研究，主要集中在股票、商品期货和沪深300股指期货等市场。如在A股市场的日内效应研究中，房振明等(2004)[10]发现收益率呈U型；韩冬等(2006)[11]发现价差呈L型，交易量呈反L型；刘衡郁(2008)[12]发现日内价格变动呈仰卧F型，交易量呈仰卧E型；鲁万波等(2011)[13]发现波动率呈倒J型，成交量呈U型，买卖价差呈J型；王春峰等(2014)[14]发现不同市值的股票交易量的日内效应不同，中、小市值呈现W型，大市值呈现U型，不同的市场环境模式也不同，牛市呈现U型，熊市呈现W型；苑莹等(2016)[15]发现上证指数和深成指数交易量的日内效应都呈现U型特征。在商品期货的研究中，刘向丽等(2008)[16]采用1分钟数据分析发现，绝对收益率和交易量的日内效应呈现L型；瞿慧等(2016)[17]发现塑料期货日内平方收益均值呈现L型。关于沪深300股指期货的研究相对丰富。如孙便霞等(2012)[18]发现日内波动呈现出3V型特征；余臻等(2014)[19]发现收益率呈L型，波动率呈LM型，日内交易量呈3V型，日内持仓量呈M型；赵秀娟等(2015)[20]发现绝对收益率呈LM型、日内成交量呈WV型、持仓量呈倒U型和价差呈LM型日内特征；郭建峰等(2016)[21]发现交易持续时间和市场弹性呈向右上倾斜的W型，相对差价、已实现波动率和交易量呈向右下倾斜的M型，市场深度呈向右上倾斜的倒S型，持仓量呈向右下倾斜的闪电型；西村友作等(2016)[22]发现沪深300指数的交易量呈U型，波动率大致为S型，股指期货的交易量和波动率大致呈3V(VVV)型。

(二)变量之间的动态关系

微观结构变量间的动态关系研究相对日内效应的研究较少，但也有不少成果出现。如华仁海等(2003)[23]研究我国商品期货市场收益率、交易量和波动性的动态关系，通过格兰杰因果检验方法发现，只有铜期货存在从绝对收益率到交易量的原因；刘向丽等(2008)[16]采用格兰杰因果检验、方差分解和脉冲响应函数等方法分析变量之间的动态关系，发现绝对收益率、交易量和持仓量之间存在双向的格兰杰因果关系，持仓量对绝对收益率和交易量的影响较弱，而绝对收益率和交易量之间有较强的互动关系；仲伟俊等(2008)[24]研究波动性与收益率、交易量和持仓量的关系，通过回归分析发现，正收益率和交易量对波动率有正向影响，负收益率和持仓量对波动率有负向影响；Kumar等(2010)[25]建立VAR模型，结合格兰杰因果检验、方差分解和脉冲响应函数分析印度商品期货市场中的波动率、交易量和持仓量之间的动态关系，发现波动率和交易量之间有较强的关系，持仓量与前两者的关系较弱；张苏林(2012)[26]研究发现沪深300股指期货的交易量和波动率没有明显的格兰杰因果关系；Liu等(2015)[27]研究发现收益率、交易量和持仓量之间存在双向的格兰杰因果关系，通过脉冲响应方法和方差分解方法发现持仓量与绝对收益率和交易量的关系较弱，绝对收益率和交易量有较强的相关性。

(三)文献综述简析

通过分析以上研究成果发现：国内外的研究主要集中在股票市场和期货市场；微观结构变量主要包括收益率、波动率、交易量和相对价差等；收益率和交易量的日内效应大部分呈U型，波动率和相对价差在不同的市场呈现不同的日内特征；收益率、波动率和交易量之间具有较强的动态相关性，持仓量与其他变量的关系较弱。

同时，也发现了以往研究的局限性：首先，国内市场主要研究了股票市场和沪深300股指期货市场，对于刚上市的上证50股指期货的研究还相对较少；其次，较少的研究考虑到微观结构变量日内效应的变化情况，几乎没有探讨过交易制度变化对日内效应和动态关系的影响。

三、研究模型与方法

1.GK模型

参考Garman等(1980)[28]的做法，采用GK模型来衡量分钟波动率，表达式如下：

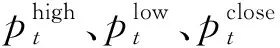
2.Wilcoxon秩和检验方法

Wilcoxon(1945)[29]提出Wilcoxon秩和检验方法，该方法是基于样本数据秩和的一种非参数检验方法，不需要预先知道样本的分布情况，相比参数化检验方法适用性更大。由于高频数据通常拒绝正态分布假设，且存在序列相关和条件异方差性，用带虚拟变量的线性回归将是有偏的，因此，本文选用Wilcoxon秩和检验方法分析序列的差异。

3.格兰杰因果检验方法

Granger(1969)[30]提出了一个判断因果关系的检验方法，用于分析变量之间的相关关系，即格兰杰因果检验。关于x是否为y的格兰杰原因的问题，主要是看过去的x能够在多大程度上解释现在的y，加入x的滞后值之后是否使解释程度提高。如果x在y的预测中有帮助，或者x与y在统计上的相关系数显著，可表述为x是y的格兰杰原因。

4.广义脉冲响应函数方法

对于VAR模型的动态过程分析，通常不考虑变量的变化对其他变量的影响，而是研究误差项变化，或者模型受到某种冲击时对整个系统的动态影响，称为脉冲响应函数方法。传统的脉冲响应函数一般需要应用Cholesky分解方法实现正交化，但是Cholesky分解的结果与变量的顺序有关，使得结果的唯一性不能保证。Koop等(1996)[31]提出广义脉冲响应函数，解决了上述问题。

四、研究数据

本文选用上证50股指期货当月连续合约，采用上市交易满一周年的1分钟高频数据进行实证研究。研究的微观结构特征变量包括：价格(p_ih)、收益率(r_ih)、波动率(gk_ih)、交易量(volume_ih)和持仓量(oi_ih)。

(一)区间划分

总样本区间为2015.04.16—2016.04.15。根据交易制度的变化，将总样本区间分为三个子区间：

(1)区间1(2015.04.16—2015.09.02)：首个交易日到严格限仓政策推出前。采用1分钟的时间间隔把一天的交易时间分割成271份，即分成D1(9:15)，D2(9:16)，……，D270(15:14)，D271(15:15)，共计271个时段。

(2)区间2(2015.09.07—2015.12.31)：严格限仓政策推出后到交易时间同步指数政策推出前。时段的划分同区间1。

(3)区间3(2016.01.04—2016.04.15)：交易时间同步指数政策推出后到上市交易满一周年。采用1分钟的时间间隔把一天的交易时间分割成241份，即分成D16(9:30)，D17(9:31)，……，D255(14:59)，D256(15:00)，共计241个时段。

(二)描述性统计

在分析日内效应及动态关系前，先对微观结构变量的日频数据进行简要的统计分析，如图1和表1所示。

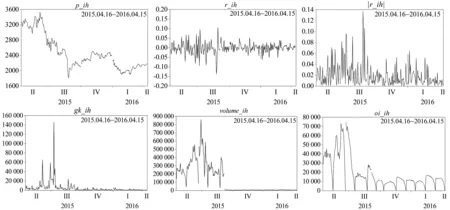
图1 微观结构变量的日频走势

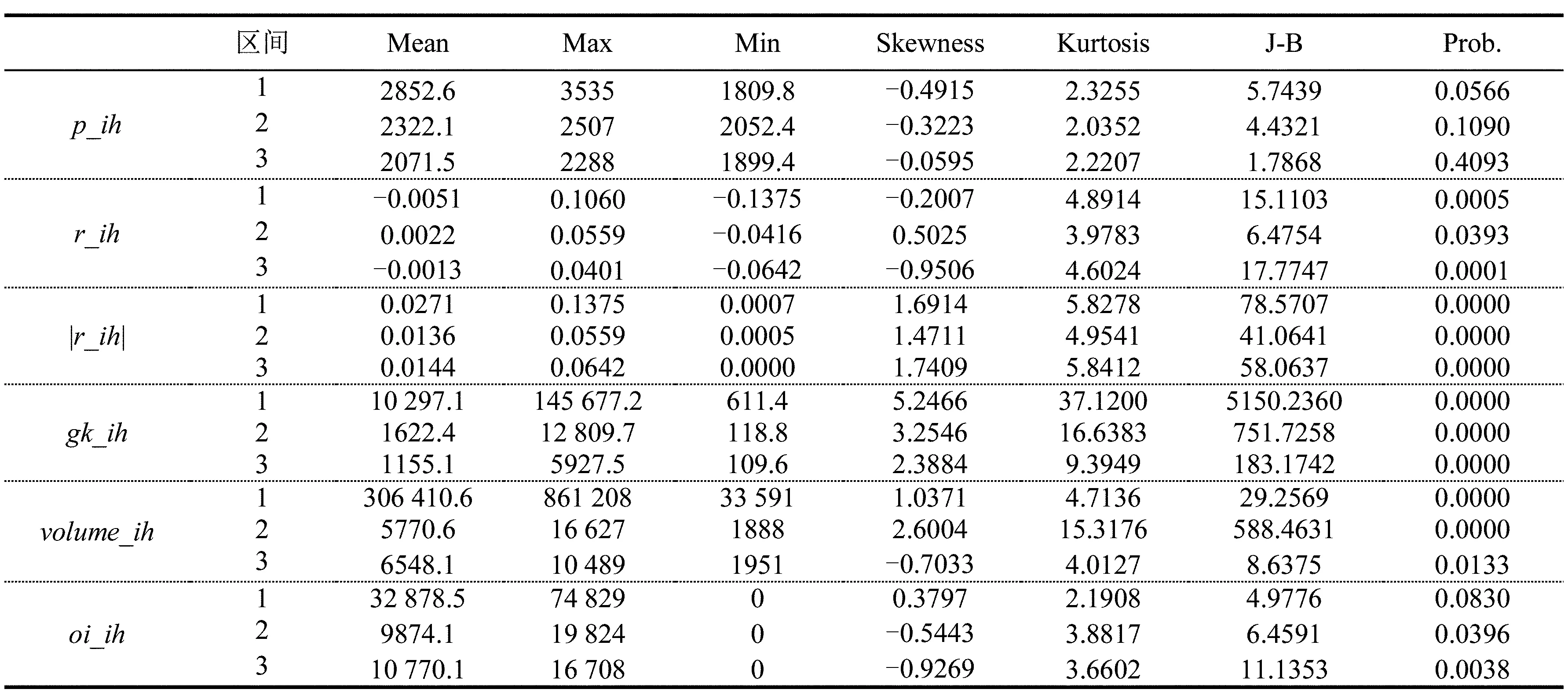
由图1可见，价格序列在区间1有较长时间且较大幅度的下跌，在区间2先涨后跌，在区间3有小幅上涨；收益率序列和绝对收益率序列在区间1有较大波动，在区间2和区间3的波动较小；波动率在区间1的波动幅度较大，在区间2和区间3的波动幅度较小；交易量在区间1的规模较大，在区间2和区间3的规模很小；持仓量在区间1的规模较大，在区间2和区间3的规模较小。

由表1发现，价格序列在区间1的平均值最大，区间2次之，区间3最小，三个区间都左偏，都未出现尖峰特征，J-B统计量显示三个区间都近似服从正态分布；收益率序列在区间1和区间3的平均值为负，区间2的平均值为正，区间1和区间3左偏，区间2右偏，峰度值都大于3，呈现尖峰特征，J-B统计量显著，拒绝服从正态分布；绝对收益率在区间1的平均值最大，区间3次之，区间2最小，三个区间都右偏，呈现尖峰特征，拒绝服从正态分布；波动率在区间1的平均值最大，区间2次之，区间3最小，三个区间都右偏，呈现尖峰特征，拒绝服从正态分布；交易量在区间1的平均值大小是区间2和区间3平均值的5倍以上，差距明显；持仓量在区间1的平均值大小是区间2和区间3平均值的3倍以上，差距也比较明显。

通过分析图1和表1发现，限仓政策使得价格序列有短暂的上涨，明显降低了收益率波动，大幅降低了波动率、交易量和持仓量；交易时间与指数同步制度也使得价格序列有短暂的上涨，但是对收益率、波动率、交易量和持仓量没有明显的影响。

五、实证分析

(一)日内效应分析

为了分析变量的日内效应，选取期货上午开盘后5分钟(D1—D5)，股市上午开盘后5分钟(D16—D20)、上午收盘前5分钟(D132—D136)、下午开盘后5分钟(D137—D141)、下午收盘前5分钟(D252—D256)和期货下午收盘前5分钟(D267—D271)的时段进行研究。考虑到每天市场对信息的消化需要一定时间，因此本文选D61(10:15)作为对照组。

1.收益率

平均收益率的日内分布如图2所示。

图2 平均收益率分布

对比图2中的三个区间，发现三个区间的平均收益率没有太大差别，都是围绕0上下波动，开盘和收盘时段的平均收益率也没有出现较大变化。

所选时段平均收益率与D61的Wilcoxon秩和非参数检验结果如表2所示。

表2不同小区间分钟收益率的非参数检验结果

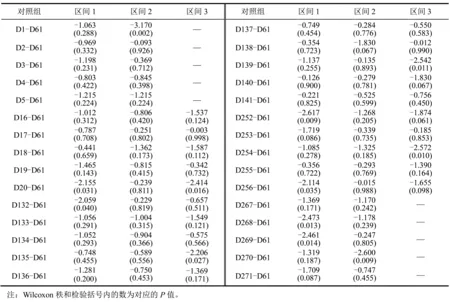
观察表2中的P值发现，区间1的对照组D252-D61和D268-D61，区间2的对照组D1-D61和D270-61，以及区间3的对照组D139-D61和D254-D61的显著性较大。

结合图2和表2可以发现，平均收益率并未呈现明显的日内效应，与Harris(1986)[1]、房振明等(2004)[10]以及余臻等(2014)[19]等研究存在较大差别，交易制度的变化也未引起平均收益率日内效应的较大变化。

为了进一步分析收益率的特征，参考Ekman(1992)[2]、Andersen等(2000)[3]和Tsuchida等(2016)[4]等的研究方法，采用绝对收益率的平均值进行研究。平均绝对收益率的分布如图3所示。

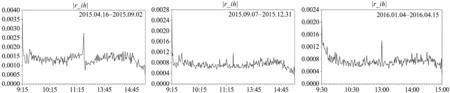
图3 平均绝对收益率分布

对比图3中的三个区间，发现三个区间的平均绝对收益率在上午开盘时段和下午开盘时段都显著高于其他时段，在下午收盘时段又都小于其他时段。以区间1为例：平均绝对收益率围绕0.0015上下波动；上午开盘时段在0.0038左右，明显大于0.0015；下午开盘时段在0.0025左右，也明显大于0.0015；下午收盘时段在0附近，明显小于0.0015。

所选时段平均绝对收益率与D61的Wilcoxon秩和非参数检验结果如表3所示。

表3不同区间分钟绝对收益率的非参数检验结果

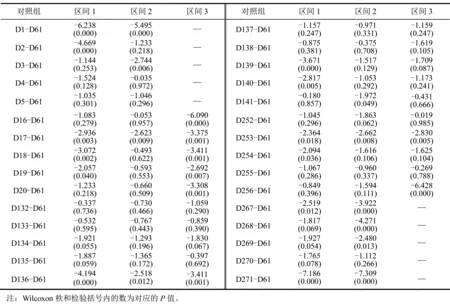
观察表3发现，区间1的对照组D1-D61、D2-D61、D136-D61和D271-D61，区间2的对照组D1-D61和D271-D61，以及区间3的对照组D16-D61和D256-D61的系数绝对值和显著性都比其他对照组大。结合图3和表3可以发现，平均绝对收益率呈现明显的日内效应：区间1大体呈现L+横向S型模式；区间2和区间3也呈现L+横向S型模式，不过下午开盘前后的峰值出现小幅下降。因此，限仓政策和交易时间同步政策对于绝对收益率的日内效应影响不大，绝对收益率的日内效应并未改变。

2.波动率

平均波动率的日内分布如图4所示。对比图4中的三个区间，发现三个区间的平均波动率都在上午开盘时段显著高于其他时段，其中区间2和区间3存在明显的日内跳跃。

所选时段平均波动率与D61的Wilcoxon秩和非参数检验结果如表4所示。

图4 平均波动率分布

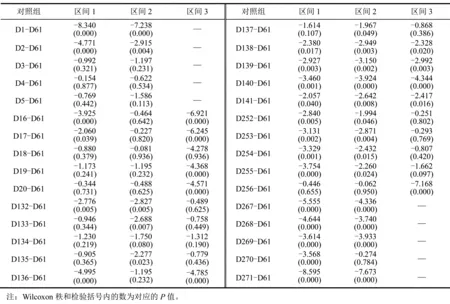
观察表4发现，区间1的对照组D1-D61和D271-D61，区间2的对照组D1-D61和D271-D61，以及区间3的对照组D16-D61、D17-D61和D256-D61的系数绝对值和显著性都比其他对照组大。

结合图4和表4可以发现，平均波动率呈现明显的日内效应：区间1呈现L型模式；区间2和区间3也大体呈现L型模式，不过日内出现较多的跳跃。因此，限仓政策和交易时间同步政策没有大幅改变平均波动率的日内效应。

3.交易量

平均交易量的日内分布如图5所示。

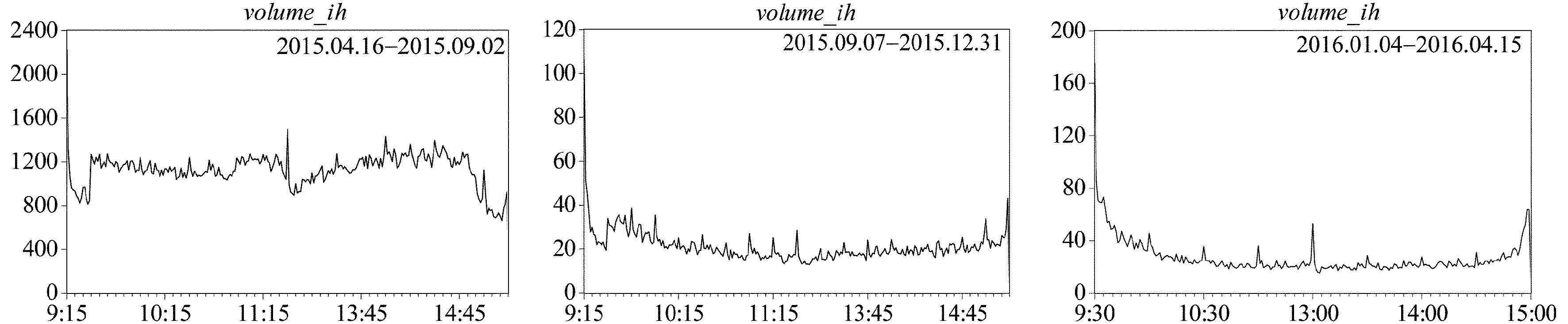
图5 平均交易量分布

对比图5中的三个区间，发现三个区间的平均交易量都在上午开盘时段显著高于其他时段，在下午收盘时段的平均交易量显著低于其他时段；区间1的平均交易量在下午开盘时段也相对较大，但是区间2和区间3并不明显。

所选时段平均交易量与D61的Wilcoxon秩和非参数检验结果如表5所示。

表5不同区间分钟交易量的非参数检验结果

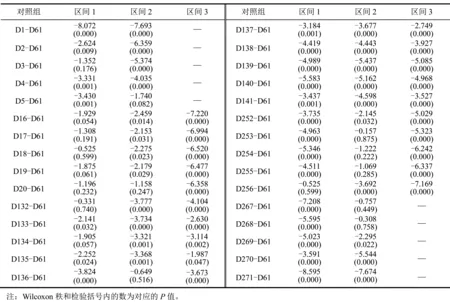
观察表5发现，区间1的对照组D1-D61、D140-D61、D254-D61、D267-D61、D268-D61、D269-D61和D271-D61，区间2的对照组D1-D61、D2-D61、D3-D61、D139-D61、D140-D61、D270-D61和D271-D61，以及区间3的对照组D16-D61、D17-D61、D18-D61、D19-D61、D20-D61、D139-D61、D253-D61、D254-D61、D255-D61和D256-D61的系数绝对值和显著性都比其他对照组大。

结合图5和表5可以发现，平均交易量呈现明显的日内效应：区间1呈现LM型模式；区间2和区间3呈现L型模式。因此，限仓政策使得平均交易量的日内效应出现了明显改变，而交易时间同步指数政策并未对平均交易量的日内效应产生较大影响。

4.持仓量

平均持仓量的日内分布如图6所示。

图6 平均持仓量分布

对比图6中的三个区间，发现区间1的平均持仓量分布明显区别于区间2和区间3，而区间2和区间3的平均持仓量分布相似。

所选时段平均持仓量与D61的Wilcoxon秩和非参数检验结果如表6所示。

表6不同区间分钟持仓量的非参数检验结果

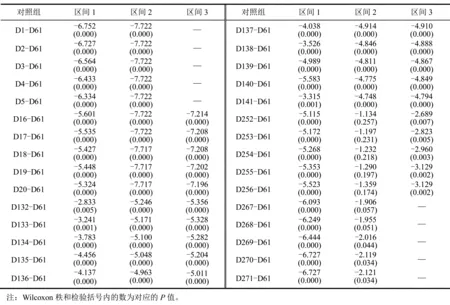
观察表6发现，区间1和区间3的所有对照组的系数绝对值和显著性都比较大，区间2的大部分对照组的系数绝对值和显著性比较大。

结合图6和表6可以发现，平均持仓量呈现明显的日内效应：区间1呈现M型模式；区间2和区间3呈现U型模式。因此，限仓政策使得平均持仓量的日内效应出现了显著改变，而交易时间同步指数政策并未对平均持仓量的日内效应产生较大影响。

(二)动态关系分析

本部分探讨交易制度改变对微观结构变量之间关系的影响。通过ADF检验发现，r_ih、gk_ih和volume_ih是平稳序列，oi_ih是单整序列I(1)，因此可以建立VAR模型。

1.引导关系检验

通过格兰杰因果检验方法分析微观结构变量之间的引导关系，结果如表7所示。

表7格兰杰因果检验

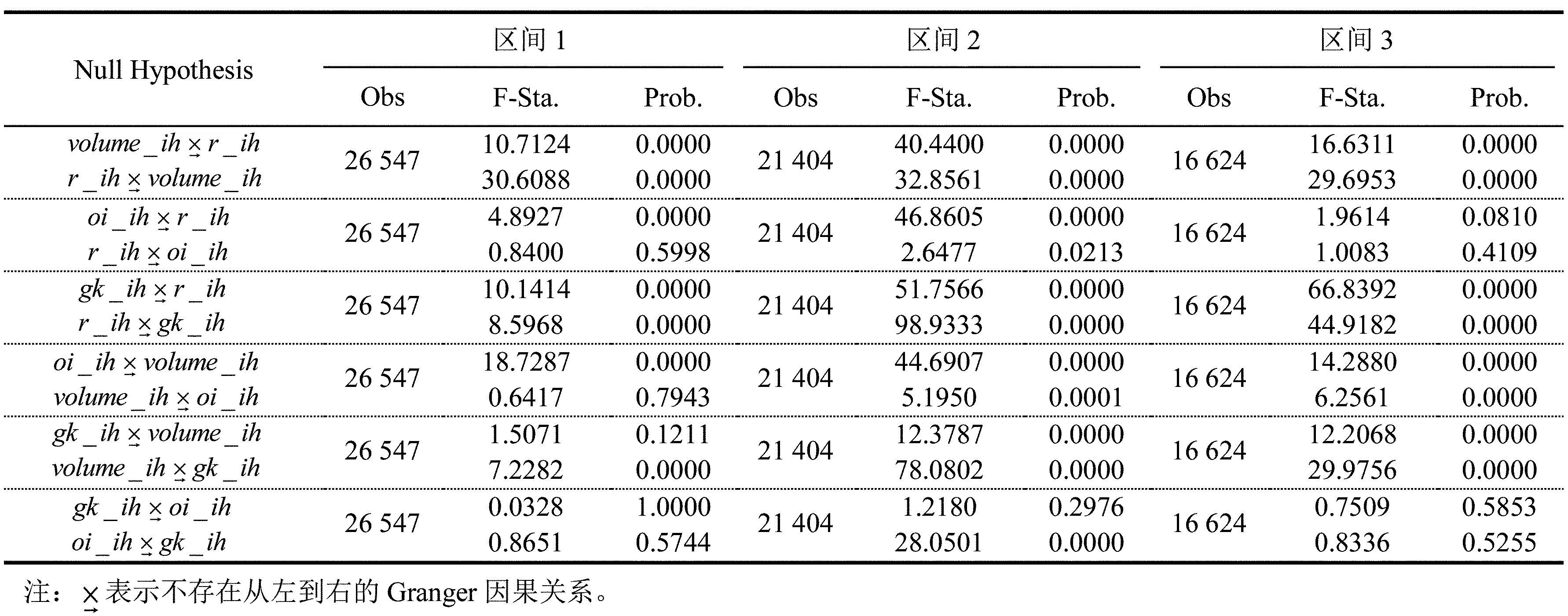
观察表7发现，交易量和绝对收益率、波动率和绝对收益率在三个区间都是互为格兰杰因果关系，说明限仓政策和交易时间同步指数政策没有改变交易量与绝对收益率、波动率与绝对收益率的引导关系。

持仓量和交易量、波动率和交易量在区间2和区间3都是互为格兰杰因果关系。在区间1中，持仓量是交易量的格兰杰原因，而交易量不是持仓量的格兰杰原因；交易量是波动率的格兰杰原因，而波动率不是交易量的格兰杰原因。说明限仓政策改变了持仓量与交易量、波动率与交易量的引导关系，而交易时间同步指数政策没有改变持仓量与交易量、波动率与交易量的引导关系。

持仓量和绝对收益率在三个区间的引导关系存在较大差别。在区间1中，持仓量是绝对收益率的格兰杰原因，而绝对收益率不是持仓量的格兰杰原因；在区间2中，持仓量是绝对收益率的格兰杰原因在1%水平显著，绝对收益率是持仓量的格兰杰原因在5%水平显著；在区间3中，持仓量是绝对收益率的格兰杰原因在10%水平显著，绝对收益率不是持仓量的格兰杰原因。说明限仓政策和交易时间同步指数政策都改变了持仓量和绝对收益率的引导关系。

波动率和持仓量在三个区间的引导关系也有显著差异。在区间1中，波动率不是持仓量的格兰杰原因，持仓量也不是波动率的格兰杰原因；在区间2中，波动率不是持仓量的格兰杰原因，而持仓量是波动率的格兰杰原因；在区间3中，波动率不是持仓量的格兰杰原因，持仓量也不是波动率的格兰杰原因。说明限仓政策和交易时间同步指数政策都改变了波动率和持仓量的引导关系。

2.广义脉冲响应分析

采用广义脉冲响应函数分析微观结构变量之间的冲击响应。

(1)区间1。区间1中的微观结构变量之间的脉冲响应，结果如图7所示。

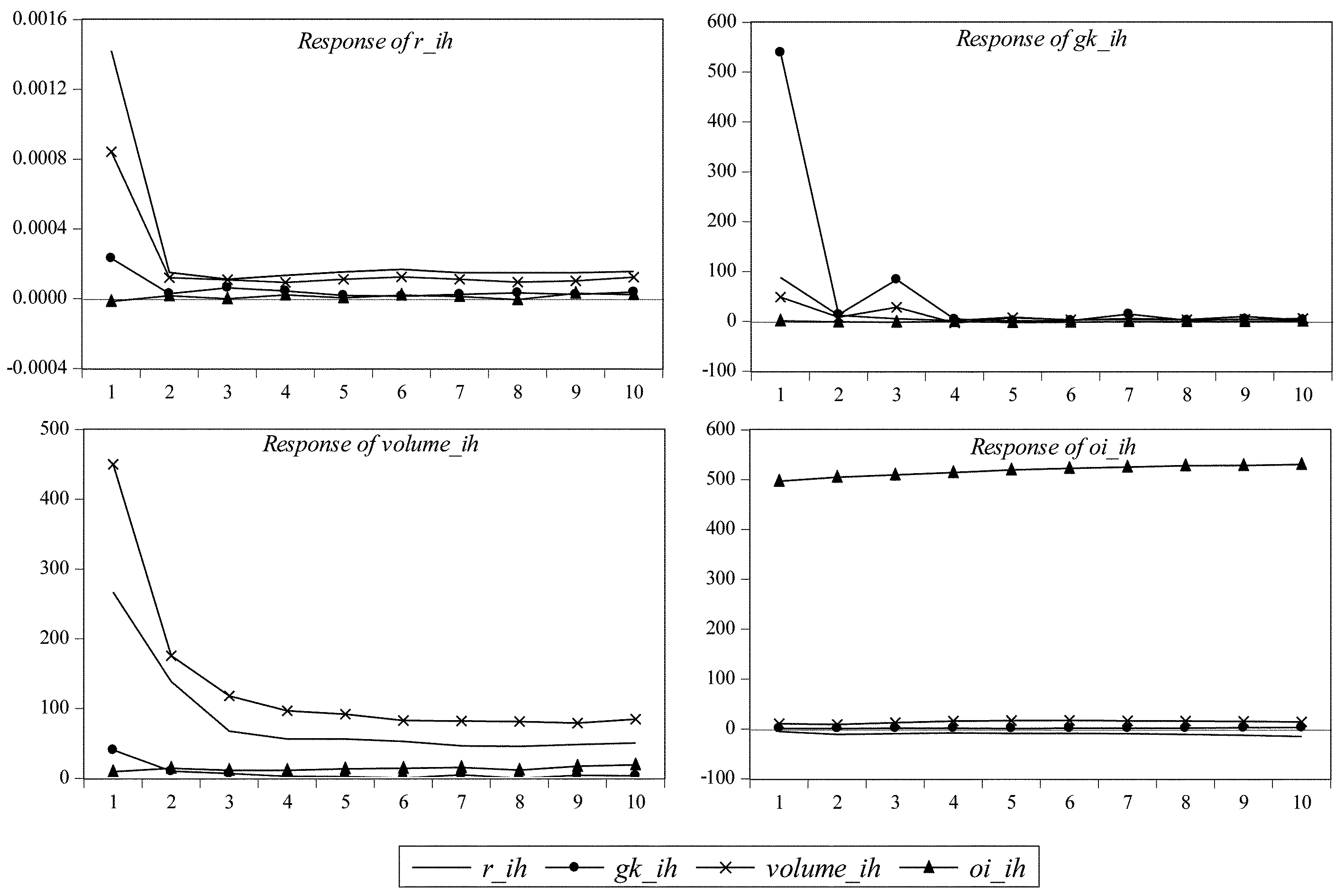
图7 区间1变量脉冲响应

绝对收益率受到自身一个标准差信息的冲击后，第1期的响应达到最大值0.0015左右，第2期降为0.0002左右；受到交易量一个标准差信息的冲击后，第1期的响应达到最大值0.0008左右，第2期降为0.0001左右；受到波动率一个标准差信息的冲击后，第1期的响应达到最大值0.0002左右，第2期降为0.000 05左右；受到持仓量一个标准差信息的冲击后，反应较弱，基本趋于0。

波动率受到自身一个标准差信息的冲击后，第1期的响应达到最大值550左右，第2期降为20左右，第3期又升到100左右，第4期降为0；受到绝对收益率一个标准差信息的冲击后，第1期的响应达到最大值100左右，第2期降为10左右，第3期降到0附近；受到交易量一个标准差信息的冲击后，第1期的响应达到最大值50左右，第2期降到0附近；受到持仓量一个标准差信息的冲击后，基本没有反应。

交易量受到自身一个标准差信息的冲击后，第1期的响应达到最大值450左右，第2期降为200左右，第3期以后维持在100左右；受到绝对收益率一个标准差信息的冲击后，第1期的响应达到最大值250左右，第2期降为150左右，第3期以后维持在50左右；受到波动率一个标准差信息的冲击后，第1期的响应达到最大值50左右，第2期降到0附近；受到持仓量一个标准差信息的冲击后，反应较弱，基本趋于0。

持仓量受到自身一个标准差信息的冲击后，一直维持在500左右；受到绝对收益率、波动率和交易量的一个标准差信息的冲击后，基本没有反应。

(2)区间2。区间2中的微观结构变量之间的脉冲响应，结果如图8所示。

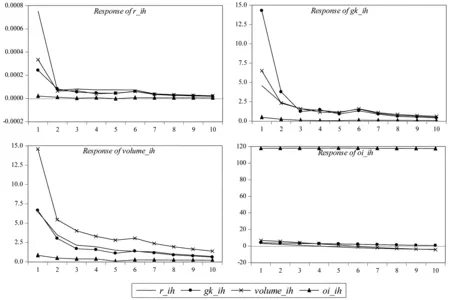
图8 区间2变量脉冲响应

绝对收益率受到自身一个标准差信息的冲击后，第1期的响应达到最大值0.0008左右，第2期降为0.0001左右；受到交易量一个标准差信息的冲击后，第1期的响应达到最大值0.0003左右，第2期降为0.0001左右；受到波动率一个标准差信息的冲击后，第1期的响应达到最大值0.0002左右，第2期降为0.0001左右；受到持仓量一个标准差信息的冲击后，反应较弱，基本趋于0。

波动率受到自身一个标准差信息的冲击后，第1期的响应达到最大值15左右，第2期降为4左右，第3期降为1左右；受到交易量一个标准差信息的冲击后，第1期的响应达到最大值7左右，第2期降为2.5左右；受到绝对收益率一个标准差信息的冲击后，第1期的响应达到最大值5左右，第2期降到2.5左右；受到持仓量一个标准差信息的冲击后，反应较弱，基本趋于0。

交易量受到自身一个标准差信息的冲击后，第1期的响应达到最大值15左右，第2期降为6左右；受到绝对收益率一个标准差信息的冲击后，第1期的响应达到最大值7左右，第2期降为3左右；受到波动率一个标准差信息的冲击后，第1期的响应达到最大值7左右，第2期降到2.5左右；受到持仓量一个标准差信息的冲击后，反应较弱，基本趋于0。

持仓量受到自身一个标准差信息的冲击后，一直维持在120附近；受到绝对收益率、波动率和交易量的一个标准差信息的冲击后，反应较弱，基本趋于0。

(3)区间3。区间3中的微观结构变量之间的脉冲响应，结果如图9所示。

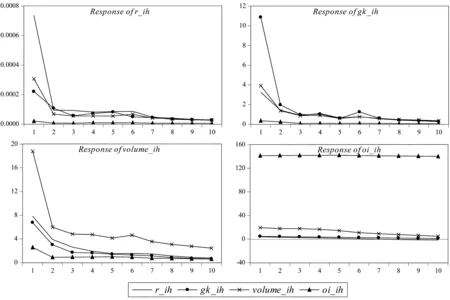
图9 区间3变量脉冲响应

绝对收益率受到自身一个标准差信息的冲击后，第1期的响应达到最大值0.000 75左右，第2期降为0.0001左右；受到交易量一个标准差信息的冲击后，第1期的响应达到最大值0.0003左右，第2期降为0.0001左右；受到波动率一个标准差信息的冲击后，第1期的响应达到最大值0.0002左右，第2期降为0.0001左右；受到持仓量一个标准差信息的冲击后，反应较弱，基本趋于0。

波动率受到自身一个标准差信息的冲击后，第1期的响应达到最大值11左右，第2期降为2左右，第3期降为1左右；受到交易量一个标准差信息的冲击后，第1期的响应达到最大值4左右，第2期降为1左右；受到绝对收益率一个标准差信息的冲击后，第1期的响应达到最大值3左右，第2期降到1左右；受到持仓量一个标准差信息的冲击后，反应较弱，基本趋于0。

交易量受到自身一个标准差信息的冲击后，第1期的响应达到最大值19左右，第2期降为6左右；受到绝对收益率一个标准差信息的冲击后，第1期的响应达到最大值8左右，第2期降为4左右；受到波动率一个标准差信息的冲击后，第1期的响应达到最大值7左右，第2期降到3左右；受到持仓量一个标准差信息的冲击后，第1期的响应达到最大值3左右，第2期降到1左右。

持仓量受到自身一个标准差信息的冲击后，一直维持在140附近；受到交易量一个标准差信息的冲击后，一直维持在20附近；受到绝对收益率和波动率的一个标准差信息的冲击后，反应较弱，基本趋于0。

六、结 语

本文主要讨论上证50股指期货日内微观结构，以及受到限仓政策和交易时间同步指数政策变动的影响，选取1分钟高频数据进行实证分析。采用Wilcoxon秩和检验非参数方法检验不同时段各变量的差异，对比变量日内效应的变化。在VAR模型的基础上，借助格兰杰因果检验方法和广义脉冲响应方法分析变量之间的动态关系变化。研究结果如下：

(1)平均收益率并未呈现明显的日内效应，而平均绝对收益率呈现明显的日内效应：三个区间都呈现L+横向S型。限仓政策和交易时间同步政策对于收益率的日内效应影响不大，收益率的日内效应并未改变。

(2)平均波动率呈现明显的日内效应：三个区间的日内效应都呈现L型。限仓政策和交易时间同步政策没有大幅改变波动率的日内效应。

(3)平均交易量呈现明显的日内效应：区间1呈现LM型；区间2和区间3呈现L型。限仓政策使得交易量的日内效应出现了明显改变，而交易时间同步指数政策并未对交易量的日内效应产生较大影响。

(4)平均持仓量呈现明显的日内效应：区间1呈现M型；区间2和区间3呈现U型。限仓政策使得持仓量的日内效应出现了显著改变，而交易时间同步指数政策并未对持仓量的日内效应产生较大影响。

(5)格兰杰因果关系检验发现：限仓政策和交易时间同步指数政策没有改变交易量与绝对收益率、波动率与绝对收益率的引导关系；限仓政策改变了持仓量与交易量、波动率与交易量的引导关系，而交易时间同步指数政策没有改变持仓量与交易量、波动率与交易量的引导关系；限仓政策和交易时间同步指数政策都改变了持仓量和绝对收益率、波动率和持仓量的引导关系。

(6)广义脉冲响应函数分析发现：绝对收益率、波动率和交易量三者之间有较强的动态关系，持仓量与其他变量的动态关系较弱；四个变量的冲击响应顺序在三个区间没有发生明显的变化，都是受到自身冲击的响应最大；而冲击响应强度区间1明显大于区间2和区间3，区间2和区间3相差不大。限仓政策明显改变了各个变量之间的冲击响应强度，而交易时间同步指数政策的影响较小。

综上所示，上证50股指期货的微观结构变量呈现出了明显的日内效应，绝对收益率、波动率和交易量三者之间有较强的动态关系，而持仓量与其他变量的动态关系较弱。限仓政策对日内微观结构的影响较大，显著改变了部分变量的日内效应和变量之间的动态关系，而交易时间同步指数政策对日内微观结构的影响较小。为了检验研究的稳健性，本文进一步对比分析了沪深300股指期货和中证500股指期货的日内微观结构及受到政策变动的影响，也得出了与上证50股指期货相似的结论。本研究具有一定的现实意义：首先，对于市场监管者检验政策实施效果、维护市场稳定具有借鉴意义；其次，投资者可以依据微观结构变量的日内效应及变化，选择并调整响应的投资策略。