格兰杰因果关系在神经科学领域的发展及缺陷

贾欣欣

(杭州电子科技大学计算机学院，浙江杭州 310018)

因果关系作为事物之间发展变化的重要联系，揭示了事物发展变化过程中的本质特征。因果关系是科学探索的基本内容之一，无论是自然现象、社会关系还是科学理论中均存在着因果关系。

因果关系的研究方法中一个运用广泛的分析方法是格兰杰因果关系(Granger Causality)。近年来，随着格兰杰因果关系应用的不断发展，其成为生命科学领域特别是计算神经科学应用方面的重要研究方法。

1 格兰杰因果关系及研究现状

在神经科学领域，国内外对格兰杰因果关系的研究主要集中在时域格兰杰因果关系分析、频域格兰杰因果关系分析及非线性格兰杰因果关系3个方面。

1．1 格兰杰因果关系

格兰杰因果关系起源于经济领域，近年来在生命科学领域特别是神经科学领域有所发展，成为揭示时间序列之间因果影响的主要方法之一。格兰杰因果关系的思想最初源于数学家维纳(Wiener)在1956年提出的关于两个时间信号之间的因果性，其核心思想是对一个变量的预测在加入另一个变量后更准确，则后者称为前者的原因［1］。1969年，格兰杰基于维纳时间信号因果性的想法［2］，提出了经济领域中的随机过程因果性，用于分析经济变量之间的格兰杰因果关系，这就是著名的时域格兰杰因果关系。

对于两个时间序列X、Y，其之间的格兰杰因果关系可具体表述为:若根据X的过去值对X的当前时刻值进行预测时产生的预测误差的方差，大于根据时间序列X、Y的过去值预测X的当前值时产生的预测误差的方差，则Y对X有格兰杰因果影响［2－3］。

假设Xt、Yt为两个平稳的时间序列，且其均值为0，其中 t=1，2，…，N，二者的线性自回归模型可表示如下［4］

其中，a1j、d1j表示自回归模型的拟合系数;ε1t、η1t为预测误差;∑1、Γ1表示 ε1t、η1t的方差。二者的联合回归模型可描述如下

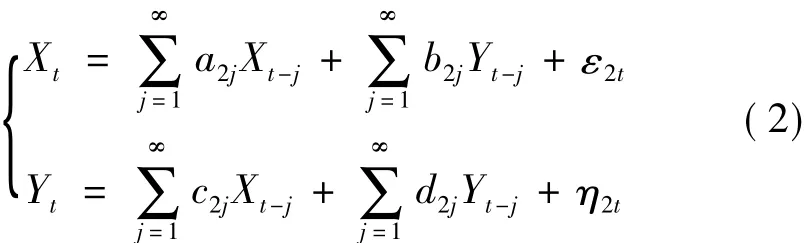
其中，a2j、b2j、c2j和 d2j表示联合回归模型的拟合系数，预测误差ε2t、η2t与时间无关，其同期协方差矩阵为

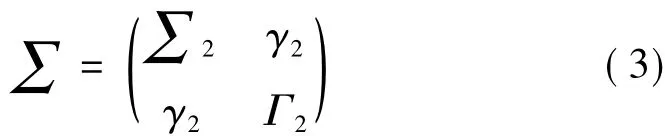
其中，∑2=var(ε2t)、Γ2=var(η2t)、γ2=cov(ε2t，η2t)，此时估计Xt、Yt当前时刻值产生的预测误差取决于两者过去时刻的值。

对于式(1)和式(2)中的第一个方程，方差∑1的值代表根据Xt自身过去时刻的值对当前时刻值进行预测的准确度，方差∑2的值表示根据Xt、Yt的过去时刻值对Xt当前时刻值的预测准确度。如果在某种统计意义上＜∑

1，那么就称Yt对Xt有因果影响。若=∑2，即加入Yt值后无法提高模型的预测精度，则称Yt对Xt没有因果影响。这种因果关系就叫做格兰杰因果关系，Yt对Xt的格兰杰因果关系定义如下

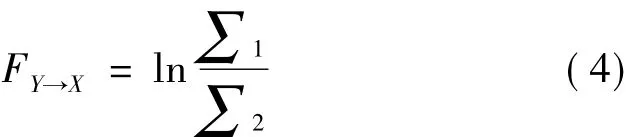
当 FY→X＞0 时，Yt对 Xt存在因果关系;当 FY→X=0时，Yt对Xt不存在因果关系。类似的，Xt对Yt的格兰杰因果关系为

当 FX→Y＞0 时，Xt对 Yt存在因果关系;当 FX→Y=0时，Xt对Yt不存在因果关系。

1．2 时域格兰杰因果关系在神经科学的发展

因果关系分析方法在神经科学领域的应用始于上世纪80年代，几十年来，对具有复杂神经网络的不同大脑区域之间因果关系的研究已经取得了一定的成果。Freiwald等［5］(1999)通过格兰杰因果关系揭示猕猴颞下皮层神经组织之间存在单向和双向的因果影响。Hesse等［6］(2003)研究了格兰杰因果关系的自适应估计，并根据时变格兰杰因果性分析了来自斯特鲁(stroop)任务的脑电图(EEG)数据，分析发现冲突情形会产生从后皮质位置向前皮质位置相互作用的密网，这一带有方向性的相互作用网主要在刺激后400 ms开始，并持续到任务结束。Roebroeck等［7］(2005)基于格兰杰因果关系映射的方法，利用功能磁共振成像(fMRI)数据来探索神经元群之间有效连接的直接影响，通过视觉运动任务仿真实验，发现神经元群体之间存在定向因果影响关系。Oya等［8］(2007)使用格兰杰因果关系分析听觉事件相关电位(ERP)的相互作用，采用神经外科病人大脑皮层的两个生理上和功能上互相相连的听觉区域的直接记录，通过声音刺激的颅内诱发电位来展示人类听觉皮质区区域之间的因果互动关系。Gow等［9］(2008)将格兰杰分析应用到有约束的核磁共振成像脑磁图和脑电图数据中，以探索词汇表达对模糊语音感知的影响，通过对文字、非文字和发音含糊不清的条目的反应，揭示出从后上颞回到整个腹侧通路处都表现出一致的直接影响。

1．3 频域格兰杰因果关系在神经科学的发展

事实上，时域格兰杰因果关系的频域分解可以在震荡的神经活动中检测因果影响。对于神经数据，不同频率段经常表现出不同的特征，上述时域的格兰杰因果关系方法被推广到频域上，发展出频域格兰杰因果关系或几种形式的类似于频率格兰杰的因果关系方法［10－12］。

Geweke［13－14］(1982)对多元自回归过程进行分解得到格兰杰因果关系的频域表示，即频域格兰杰因果关系，使格兰杰因果关系的定义更加直观。Bernasconi和Konig［15］(1999)运用Geweke的谱分析方法来检测猫视觉皮层不同区域之间的因果互动。Brovelli等［16］(2004)通过对按压杠杆的清醒着的猴子运用谱格兰杰因果关系方法，来确定β频率段为15～30 Hz时，从初级躯体感觉皮层到运动皮层的因果影响。Saito和Harashima［17］(1981)介绍定向相干性(DC)方法，研究两个变量的自回归模型中成对数据通道之间的相关性，并随后将其应用于临床问题。Wang和 Takigawa［18］(1992)根据DC方法研究大脑两个半球之间的相互关系。Kaminski和 Blinowska［19］(1991)基于频域传递函数矩阵，提出定向传递函数(DTF)法，用于进行多元数据集中任意给定的成对通道间的因果影响方向性分析。Baccal和 Sameshima［20］(2001)在频域介绍偏定向相关性(PDC)分析方法，讨论PDC的应用，并与其他根据神经生理学信号确定大脑结构关系的方法进行比较。Sato等［21］(2009)将 PDC用于功能性磁共振成像，基于不同的频域特征来区分生理和非生理元素。Yamashita等［22］(2005)运用相对功率贡献(RPC)来评估血氧信号在不同分段频率下的定向连接。Kaminski和 Liang［23］(2005)在 θ波带频率介于 3．7 ～5．6 Hz之间时，采用短时DTF来显示海马对前脑的主要影响关系。Korzeniewska等［24］(2008)采用短时 DTF，揭示在高频下参与录制语言任务的不同大脑区域的频率依赖相互作用。

1．4 非线性格兰杰因果关系的发展

格兰杰因果关系用于分析线性时间序列，弱非线性信号也可通过近似成线性信号进行讨论。研究表明，健康人的脑电信号表现出弱非线性的特征，但是在大脑受损等情况下，脑电信号则为非线性序列。因此，如何正确揭示非线性信号之间的因果性对研究大脑的信息流向极为重要［25］。

Marinazzo等［26］(2006)提出基于径向基函数的非线性格兰杰因果关系，并通过两个实例说明该方法的有效性。Marinazzo等［27］(2008)还通过运用几何中希尔伯特空间重构理论，提出处理过滤因果关系的策略，建立处理非线性因果关系的内核方法。Sugihara等［28］(2012)基于没有噪声项的非线性动态回归模型，提出交叉收敛映射(CCM)方法作为格兰杰因果关系分析方法的补充。

2 格兰杰因果关系的局限

虽格兰杰因果关系在众多领域都有广泛的应用，但该分析方法依然在许多方面受到研究人员的诟病，争论的焦点就在于格兰杰因果关系是否能揭示真实的因果关系，且格兰杰本人也表示格兰杰因果关系不一定能代表真正的因果关系。格兰杰因果关系及其他基于格兰杰因果关系的分析方法，在理论上存在如下局限性［29－31］:

在时间域上，对两个时间序列而言，经典格兰杰因果关系与线性回归模型的随机噪声项有关，而与两时间序列的线性回归模型的部分系数无关。这样此定义会丢失线性回归模型中的一部分重要信息，导致不能准确反映一个时间序列对另外一个时间序列的真实因果关系强度，也就是说，格兰杰因果关系值的大小不一定代表着真实因果关系的强弱，甚至当格兰杰因果关系值为零时也并不代表没有真正的因果关系。换句话说，无论脑电数据是否来自同一个被试者，不同组对通道数据的格兰杰因果关系值不具有可比较性。

在频率域上，频域格兰杰因果关系的定义是基于线性回归模型中的传递函数矩阵和随机噪声项。在研究过程中已经意识到，频域格兰杰因果关系不能揭示两个时间序列之间的真正因果关系。因此，在频域中各种类似格兰杰因果关系的定义被提出，其中最常用的定义有:偏定向相干性、相对功率贡献和定向传递函数。频域格兰杰因果关系只能运用于两个时间序列，偏定向相干性、相对功率贡献和定向传递函数方法可以应用于高维时间序列，但是相对功率贡献和定向传递函数不能辨别不同结构之间的直接或间接通路，偏定向相干性又缺少理论基础。以上频域格兰杰因果关系分析方法或类似频域格兰杰因果关系方法都是基于线性回归模型的传递函数矩阵或者它的逆矩阵，而传递函数矩阵与线性回归模型的系数矩阵是完全不同的，不能真实反映出某些时间序列的因果关系强度。

3 格兰杰因果关系在神经科学的应用

脑电信号相互作用的方向揭示了神经系统中信息流的路径，近年来，如何确定神经系统中脑电信号之间相互作用的方向已经成为神经科学领域研究的热点。格兰杰因果关系特别是频域格兰杰因果关系作为揭示时间序列之间因果影响的主要方法之一，在生命科学领域特别是神经科学领域得到了广泛应用。但格兰杰因果关系在以下两个方面的研究还很有限，还存在很大的应用空间。

一方面，在认知和神经科学领域，多通道脑电信号数据的记录和功能成像在研究认知和疾病诊断的网络机制中越来越重要，研究人员不仅研究特定大脑区域的功能，还关注不同大脑区域块之间的因果影响，根据多个脑区或整个大脑的信息从脑功能整合的角度探究人的大脑活动及工作机理。比如，可能会对不同的大脑区域块中的因果关系信息流方向感兴趣。即使两个单变量信号之间不存在因果影响，但其所在的信号块之间也可能会存在相互影响。经典因果关系只适用于成对单变量之间因果关系分析，或者条件于第3个变量的因果关系分析，虽然通过对成对因果分析进行叠加来实现多变量之间的因果关系分析是可能的，但其计算结果并不稳定。更加有效、理论上也更加可行的方法是，把不同大脑区域的时间序列记录结合为块，然后分析不同时间序列块之间的因果影响。通过对经典因果关系进行拓展和改进，研究块对块因果关系分析方法，不仅可定性的讨论不同的脑区间是否存在因果影响及作用方向，还可定量给出相互影响程度，更为真实的揭示大脑内部的信息处理机制。

另一方面，格兰杰因果关系基于线性回归模型，适用于线性信号之间因果关系分析和弱非线性信号之间因果关系的研究。研究表明，健康人的脑电信号表现出弱非线性的特征，但在大脑受损等情况下，脑电信号则为非线性序列。为了将块对块因果关系分析的理论方法应用于实际问题中，揭示在病理情况下不同大脑区域块之间的信息流向，更好地为人类服务，对非线性模型进行研究有更大的现实意义。目前的研究中对非线性模型的研究很有限，针对非线性模型的因果关系的研究工作有待进一步完善。

4 结束语

格兰杰因果关系特别是频域格兰杰因果关系在神经科学领域已得到了广泛应用，证明了因果关系分析方法在神经科学领域的应用价值，但格兰杰因果关系先天的缺陷和局限性限制了其进一步的应用。所以，对经典因果关系不断改进，提出新的揭示因果关系的方法，并应用于神经科学研究领域中具有重要的理论和实际意义。

［1］ 郭水霞，陈松乔．运用偏相关因果分析推断神经网络的真实结构［M］．计算机工程与应用，2007，43(25):25－27．

［2］ Granger C W J．Investigating causal relations by econometric models and cross － spectral methods［J］．Econometrica，1969(37):424－438．

［3］ Hu S，Dai G，Worrell G A，et al．Causality analysis of neural connectivity:critical examination of existing methods and advances of new methods［J］．IEEE Transactions on Neural Networks，2011，22(6):829 －844．

［4］ Ding M，Chen Y，Bressler S L．Granger causality:Basic theory and applications to neuroscience［M］．Weinheim，Germany:Wiley－VCH，2006．

［5］ Freiwald W A，Valdes P，Bosch J，et al．Testing non － linearity and directedness of in teractions between neural groups in the macaque inferotemporal cortex ［J］．Neuroscicnce Methods，1999，94(1):105 －119．

［6］ Hesse W，Möller E，Arnold M，et al．The use of time－variant EEG Granger causality for inspecting directed interdependencies of neural assemblies［J］．Neuroscicnce Methods，2003，124(1):27－44．

［7］ Roebroeck A，Formisano E，Goebel R．Mapping directed influence over the brain using Granger causality and fMRI［J］．Neuroimage，2005，25(1):230 －242．

［8］ Oya H，Poon P W F，Brugge J F，et al．Functional connections between auditory cortical fields in humans revealed by Granger causality analysis of intracranial evoked potentials to sounds:comparison of two methods［J］．Biosystems，2007，89(1－3):198－207．

［9］ Gow W，Segawa J A，Alfhors S，et al．Lexical influences on speech perception:a granger causality analysis of MEG and EEG source estimates［J］．Neuroimage，2008，43(3):614 －623．

［10］ Chen T，Bressler S L，Ding M．Frequency decomposition of conditional granger causality and application to multivariate neural field potential data ［J］．Journal of Neuroscience Methods，2006，150(2):228 －237．

［11］ Guo S，Wu J，Ding M，et al．Uncovering interactions in the frequency domain ［J］．Plos Computational Biology，2008，4(5):1－5．

［12］ He F，Billings S A，Wei H，et al．A nonlinear causality measure in the frequency domain:Nonlinear partial directed coherence with applications to EEG ［J］．Journal of Neuroscience Methods，2014，22(5):71 －80．

［13］ Geweke J．Measurement of linear dependence and feedback between multiple time series［J］．Journal of America State Association，1982，77(378):304 －313．

［14］ Geweke J．Measures of conditional linear dependence and feedback between time series［J］．Journal of America State Association，1984，79(388):907 －915．

［15］ Bernasconi C，Konig P．On the directionality of cortical interactions studied by structural analysis of electrophysiological recordings［J］．Biology Cybern，1999，81(3):199 －210．

［16］ Brovelli A，Ding M，Ledberg A，et al．Beta oscillations in a large－scale sensorimotor cortical network:Directional influences revealed by Granger Causality［J］．Nat．Acad．Sci．U－nited States of America，2004，101(26):9849 －9854．

［17］ Saito Y，Harashima H．Tracking of information within multichannel EEG record［M］．Amsterdam，Elsevier:1981．

［18］ Wang G，Takigawa M．Directed coherence as a measure of interhemispheric correlation of EEG［J］．International Journal of Psychophysiol，1992(13):119 －128．

［19］ Kaminski M J，Blinowska K J．A new method of the description of the information flow in the brain structures［J］．Biology Cybern，1991(65):203 －210．

［20］ Baccal L A，Sameshima K．Partial directed coherence:A new concept in neural structure determination ［J］．Biology Cybern，2001，84(6):463 －474．

［21］ Sato J R，Takahashi D Y，Arcuri S M，et al．Frequency domain connectivity identification:an application of partial directed coherence in fMRI［J］．Human Brain Mapp，2009，30(2):452－461．

［22］ Yamashita O，Sadato N，Okada T，et al．Evaluating frequency－wise directed connectivity of bold signals applying relative power contribution with the linear multivariate time－series models［J］．Neuroimage，2005(25):478 － 490．

［23］ Kaminski M，Liang H．Causal influence:Advances in neurosignal analysis［J］．Critical Review Biomed，2005，33(4):347－430．

［24］ Korzeniewska A，Crainiceanu C M，Kus R，et al．Dynamics of event－ related causality in brain electrical activity［J］．Human Brain Mapp，2008，29(10):1170 －1192．

［25］李颖洁．脑电信号分析方法及其应用［M］．北京:科学出版社，2009．

［26］ Marinazzo D，Pellicoro M，Stramaglia S．Nonlinear parametric model for granger causality of time series［J］．Physics Review E，2006(73):066216－1－066216－6．

［27］ Marinazzo D，Pellicoro M，Stramaglia S．Kernel method for nonlinear granger causality ［J］．Physical Review Letters，2008，100(14):144103 －1 －4．

［28］ Sugihara1 G，May R，Ye H，et al．Detecting causality in complex ecosystems［J］．Science，2012，338(6106):496 －500．

［29］ Hu S，Cao Y，Zhang J，et al．Granger causality's shortcomings and new causality measure ［J］．Cognitive Neurodynamics，2012(6):33－42．

［30］ Hu S，Cao Y，Zhang J，et al．Evidence for existence of real causality in the case of zero granger causality［C］．Nanjing:ICIST，2011:1385 －1389．

［31］ Hu S，Liang H．Causality analysis of neural connectivity:new tool and limitations of spectral granger causality［J］．Neurocomputing，2012(76):44 －47．