等静压成型陶瓷义齿坯体制造及测量仿真研究

2018-10-22白国栋

机械设计与制造 2018年10期

陈桦，白国栋，张耿

（西安工业大学机电工程学院，陕西西安 710021）

1 引言

由于陶瓷义齿的高度仿真性，深受某牙医和患者的青睐。目前陶瓷义齿采用CAD/CAM系统制作。国内某大学科研人员在义齿修复体的计算机辅助设计与制造方面做出了大量的研究，为国内CAD/CAM系统在口腔修复领域的应用做出了贡献[1]。对于义齿模型的构建，文献[2-3]在义齿模型的重构和CAM工艺生成方面做出了深入的研究。由于陶瓷义齿制作采用的CAD/CAM系统研发难度大、义齿加工工艺路线生成复杂、切削过程难以掌控，因此，造成目前陶瓷义齿的价格仍然昂贵。针对目前陶瓷义齿制作过程中存在的众多问题，尝试采用等静压成型技术来制作陶瓷义齿坯体的一种新型制作方法。等静压成型技术具备可成型复杂形状的零件、生产效率高和模具生产成本低等突出优点，逐渐成为特殊零件的一种生产方式。某大学在碳化硅的等静压成型工艺及成型坯体的性能测试方面做出了大量的研究工作[4]。由于复杂形状坯体的等静压成型过程中存在多种影响因素，不能采用传统依靠经验的反复静压成型方式。为了减少成型过程中资源的浪费，同时，又能保证成型产品的质量，将计算机仿真技术应用到等静压成型过程中来就显得极为必要。文献[5]使用有限元法模拟了粉末成型过程中坯体形状尺寸及收缩率的变化。文献[6]采用了ABAQUS软件仿真了Al2O3成型过程中的应力场分布情况。

2 等静压成型仿真分析

2.1 材料模型建立

由于陶瓷粉末中含有大量的空隙，是一种非连续类型材料，在受到压力的作用时粉末中的空隙逐渐收缩，导致粉体的密度逐渐增加。这一特性与土体在屈服的时候具有相同的变化性质，因此，应用于岩土力学上的多种弹塑性模型就可以拓展到这种多空隙的粉末材料压制变形的过程中。等静压成型过程中的陶瓷粉末选择常用弹塑性模型中的Drucker-Prager-Cap（DPC）模型[7-8]，如图1所示。该模型曲线由线性阶段、过渡阶段和帽盖阶段组成。线性阶段是粉末在受到静压力下发生变形，该阶段可视为弹性变形，当静压力达到一定值后，粉末就会出现屈服现象，发生塑性变形，即曲线中的帽盖阶段，为了避免在数值计算过程中出现不稳定情况，在线性阶段和帽盖变形阶段之间存在一个过渡阶段。

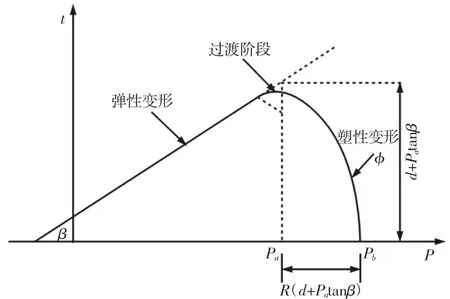
图1 Drucker-Prager-Cap模型Fig.1 Drucker-Prager-Cap Model

上述曲线图中帽盖屈服面的计算公式：

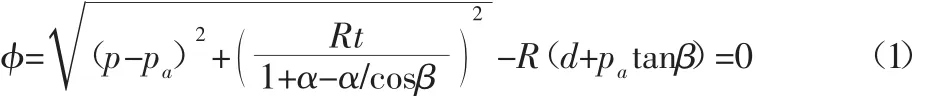
式中：p—流体静压力；

t—一个不变压力；

tanβ—弹性阶段的线性直线的斜率；

d—用来描述粉末之间的凝聚力；

R—帽盖模型的参数；

α—用来描述介于弹性阶段和塑性阶段的过渡阶段的参数；

pa—屈服表面的初始位置参数。

2.2 材料模型参数设定

针对陶瓷粉末等静压仿真过程中Drucker-Prager-Cap模型的参数及材料属性进行设置，陶瓷粉末材料模型的弹性模量为9.5GPa，泊松比为0.28。DPC模型中材料属性参数，如表1所示。

表1 DPC模型中材料属性参数Tab.1 Material Property Parameters of DPC Model

2.3 等静压成型过程仿真

义齿坯体的等静压成型过程是将干燥成型好的陶瓷义齿坯体，装入橡胶包套中放入等静压机中进行压制。该过程中义齿坯体是完全浸入在液体介质中，会受到各个方向上大小相等的压力的作用，方向垂直于义齿各个部位的表面。使用有限元分析法来仿真义齿坯体的成型过程，需要将该义齿坯体的压制过程进行模型等效[9]。由于义齿模型中的牙冠部分是最终目标所得，而牙冠下方的凸台则是为了避免在夹取过程中损伤牙冠而设置的辅助结构。因此，在设置义齿模型的边界条件时，对模型底面进行X、Y、Z三个方向上的移动和转动约束，模型除了底面之外的其他表面全部施加载荷约束，选取载荷类型中的压强完成静压力的施加。主要研究分析义齿坯体的牙冠部分位移变形情况。

2.4 仿真结果分析

义齿坯体的等静压成型目的是为掌握义齿坯体在等静压成型前后形状和尺寸上的变化。通过有限元仿真分析对等静压成型实验进行理论上的指导，并对实验过程中义齿坯体的形状变化进行预测。在仿真结果中选择输出位移变化结果。变形前后的位移云图，如图2所示。

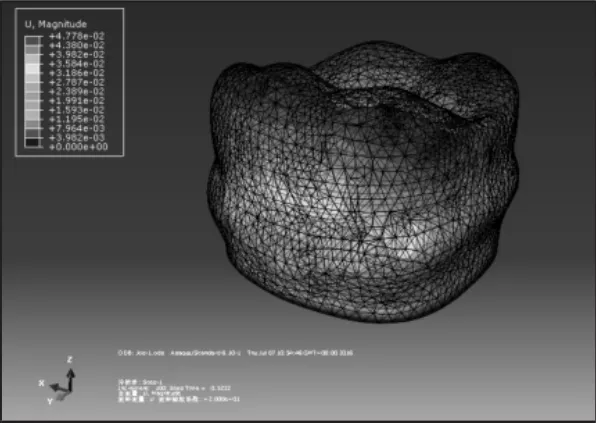
图2 变形前后的位移对比云图Fig.2 Displacement Nephggram Before and After Deformation

从仿真结果分析，由于义齿模型的牙冠部分表面有多处牙尖，牙冠中间部位存在较深的窝洞，结构并不规则，因此受到来自各个方向的压力时，牙冠部分结构形状会产生较大的位移变化，结果中的红色部分显示。模型中牙冠部分下方的凸台，形状近似为立体，结构相对比较规则，在压缩过程中凸台的整体形状和尺寸只产生了较小的变化，结果中绿色部分显示。鉴于凸台为牙冠制作过程中的辅助性结构，因此主要关注义齿坯体中牙冠部分的形状变化。结果显示，牙冠部分收缩量较大，牙冠表面5处牙尖的收缩量一致，牙冠表面3处窝洞的收缩量一致，牙冠周身处的收缩量也一致。义齿牙冠处关键位置处的收缩量，如表2所示。

表2 牙冠处关键位置收缩量Tab.2 Dental Crowns Key Position Shrinkage

由于牙冠各位置处收缩量偏差为3.890e-03mm，在误差允许范围内。因此，牙冠部分的收缩情况可以采用统一收缩率来描述。收缩过程没有产生畸形变化，收缩后也比较符合真实的牙齿亚冠形状。因此，从计算机仿真角度出发，采用等静压成型技术来压制陶瓷义齿坯体的方法是可行的。

3 等静压成型实验

3.1 义齿坯体成型

陶瓷义齿坯体等静压成型采用的技术路线为：先干燥成型出义齿坯体，再等静压成型压制出义齿坯体。在义齿坯体的凝固成型阶段采用增材制造技术制作出的义齿专用模具满足精度上的要求[10]。将配置好的医用生物陶瓷浆料注入到义齿模具中，静置、干燥、脱模得到成型的义齿坯体。该阶段成型出来的义齿坯体满足真实义齿的形状，但不具有任何的强度和硬度。干燥成型出的义齿坯体，如图3所示。

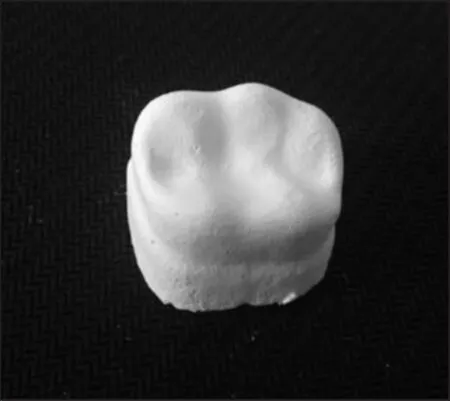
图3 干燥成型的义齿坯体Fig.3 Denture Body of Dry Forming

3.2 义齿坯体等静压成型

将干燥成型出的义齿坯体装入橡胶包套中，对其进行抽真空后捆扎密封。将其放入等静压机中进行等静压成型。等静压成型过程中的实验参数设置，如表3所示。

表3 等静压实验参数Tab.3 Isostatic Pressing Experimental Parameters

为了保证成型好的义齿坯体在卸压过程中不出现裂缝和断层现象，因此压力不能瞬间卸掉，需要分阶段缓慢卸压，第一阶段在25s之内使压力从250MPa降至150MPa，接着第二阶段在15s内从150MPa降至0MPa。等静压成型出的陶瓷义齿坯体的，如图4所示。从压制结果分析，成型出的义齿坯体表面光滑，组织致密，结构形状并没有发生畸形变化，符合真实牙齿的牙冠特征。从实验角度证实了等静压成型技术压制陶瓷义齿坯体方法的可行性。

图4 等静压成型出的义齿坯体Fig.4 Denture Body of Isostatic Pressing Forming

4 义齿坯体的测量

4.1 义齿坯体测量方案确定

采用等静压成型方法压制义齿坯体的过程中，由于粉末的孔隙结构，在成型前后义齿坯体会发生形状上的收缩。通过对等静压前后义齿坯体形状尺寸的测量，掌握成型过程中义齿坯体的收缩量。由于义齿模型的结构不规则，表面形状比较复杂。因此，对义齿进行全方位的测量及得到精确的收缩率不太容易实现。鉴于主要研究义齿牙冠部分的收缩情况，因此通过测量义齿牙冠部分关键点处的尺寸变化，进而推算出义齿牙冠整体的收缩情况。

采用三坐标测量仪主要针对义齿坯体的牙冠部分进行测量。为了更精确的测量义齿牙冠部分的尺寸，在牙冠的方向、Y方向、齿面所处的Z方向上选取了10处关键点，如图5所示。X0代表牙冠X方向上的长度最大尺寸点，Y0代表牙冠Y方向上的长度最大尺寸点。Z1、Z2、Z3、Z4、Z5分别代表亚冠上第一、二、三、四、五个牙尖处在轴上的最大高度点。Z6、Z7、Z8分别代表牙冠上第一、二、三个窝洞在Z上的最小高度点。

图5 义齿坯体测量点标记Fig.5 Denture Body Measurement Point Mark

4.2 义齿坯体的测量结果

等静压成型之前的义齿坯体的测量结果，如表4所示。

表4 静压成型之前的义齿坯体的10个标记点处尺寸（mm）Tab.4 10 Points Size of Denture Body Before Isostatic Pressing Forming（mm）

等静压成型之后的义齿坯体的测量结果，如表5所示。

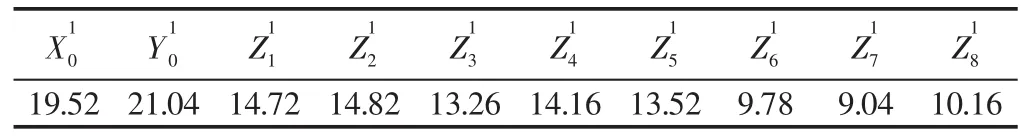
表5 静压成型之后的义齿坯体的10个标记点处尺寸（mm）Tab.5 10 Points Size of Denture Body After Isostatic Pressing Forming（mm）

由于义齿牙冠表面为不规则曲面构成，在考虑曲面的完整收缩时，收缩率计算太过复杂。因此，可以采用有限元法思想，将曲面理解为众多小曲面拼接而成，可以认为每一个小曲面都是沿其法线方向线性变化，用小曲面上关键点的尺寸变化来显示。因此可以用线性收缩率来近似计算这10处标记点的收缩情况，线性收缩的计算公式为：

式中：S—产品的收缩率（%）；

L0—等静压成型之前零件尺寸；

L—等静压成型之后零件尺寸。

义齿表面10个标记点处的收缩率，如表6所示。

表6 义齿坯体上10个标记点处的收缩率%Tab.6 10 Points Shrinkage of Denture Body

4.3 测量实验结果分析

由于义齿坯体的压制采用的等静压成型法最大特点就是对浸入液体介质中的物体从各个方向产生大小相等的压力，且压力的方向沿物体表面的法线方向。从理论角度出发，义齿坯体的各个部分的收缩率应该是统一的，可以用一个统一的收缩率来表示义齿整体的收缩。义齿坯体各标记点处的收缩率与统一收缩率的对比，如图6所示。

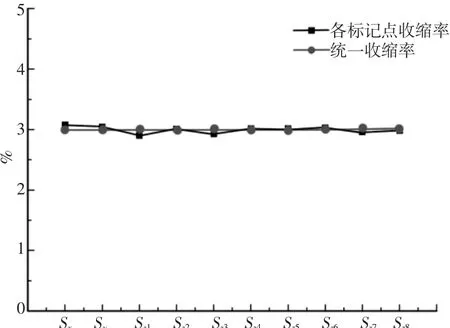
图6 义齿坯体各点处收缩率与统一收缩率的对比Fig.6 Contrast between Each Point’s Shrinkage of Denture Body and Uniform Shrinkage

通过测量计算得到上述10个标记点处的收缩率并不一致，收缩率产生波动的原因有以下两种：

（1）义齿坯体的结构复杂，形状及其不规整，义齿的和方向的长度尺寸不同，义齿坯体表面的各测量点在轴方向的上的高度尺寸不同，即使在各个方向上受到压力大小相等，但是由于义齿坯体在各部位尺寸的差异，因此传递到义齿内部不同位置处的压力值有少量差异，导致不同位置关键点处的最终收缩率产生波动。

（2）在等静压过程中，义齿坯体内部的陶瓷粉末的相对滑动、粘结和固化等复杂的变化规律也可能引起义齿不同位置处的粉体收缩率的不同。

由于，所选取的这10处标记点涵盖了义齿牙冠X、Y、Z三个方向上的尺寸，因此，这10处的标记点的收缩率也体现了义齿牙冠三个方向上的尺寸变化。通过对收缩率结果分析，义齿坯体10处标记点的平均收缩率为2.996%，收缩率变化最大的义齿X轴方向的收缩率为3.078%，收缩率变化最小的义齿Z轴方向第一个牙尖处的收缩率为2.902%。义齿坯体测量的标记点中，收缩率最大处与最小处相差0.176%，鉴于义齿结构尺寸较小，0.176%的收缩率变化在误差允许范围内。这种收缩变化的情况下，为了便于义齿模具制作中的误差补偿，可以近似看作义齿坯体的平均收缩率为3%，因此，用统一的收缩率3%来表示义齿坯体的各个部分及整体的收缩变化。这也从实验角度证实了在等静压成型过程中可以用统一的收缩率来表示义齿坯体的收缩变化。