一种两自由度并联机构的动力学分析

2018-10-22韩旭炤陈阳阳

机械设计与制造 2018年10期

韩旭炤，陈阳阳，高峰，田璐

（西安理工大学机械与精密仪器工程学院，陕西西安 710048）

1 引言

并联机构具有承载能力强、刚度大、无累积误差、运动精度高、动态性能好等一系列优点引起了国内外学者的普遍关注[1-2]。特别是少自由度并联机构在机床及其机器人上的广泛应用，使得人们针对少自由度并联机构的研究成为一个热门的科研课题。

并联机构的动力学建模是其动力学性能优化和控制等相关研究的基础，主要分为动力学正问题和逆问题两个方面。由于并联机构动力学正问题的分析建模过程比较复杂，而且在工程应用中也不经常使用，因此相关研究较少。与正问题相反，构建并联机构的动力学逆问题模型相对简单，且应用面广，是动力学性能分析、动力学参数识别、驱动电机选型和动力学控制等研究的基础，国内外相关研究也比较全面。

目前常用的动力学建模方法主要有拉格朗日方程法、牛顿—欧拉法、凯恩法和虚功原理法等。牛顿—欧拉法[3-4]具有递推形式，适合数值计算，其物理意义明确，但需求出机构的铰链内力，因此计算工作量较大；拉格朗日方程法[5-6]获得的动力学模型形式标准，但在计算过程中涉及到大量的偏微分推导与运算，过程太过繁琐容易出错，而且要进行大量的编程运算；而基于动力学普遍方程的虚功原理[7-8]和凯恩方程[9-10]建模相对简单，是建立并联机构动力学模型的常用方法。由雅可比矩阵和海赛矩阵可导出操作空间与关节空间的速度和加速度之间的映射关系，由此可方便导出机构中各运动构件的广义速度与广义力。同时，利用凯恩方程进行动力学建模时，推导过程清晰，方便进行编程计算，使动力学逆向问题的求解计算效率得到较大提高。

针对一种三杆二自由度平面运动并联机构进行了深入的研究，详细推导了该机构的位置逆解、速度及加速度方程，并给出了该机构的雅克比矩阵，推导了该并联机构主要零部件的偏速度和偏角速度矩阵方程，采用凯恩法建立了该并联机构的动力学逆解模型。最后通过数值计算与ADAMS仿真相结合的方法验证了所建模型的正确性。

2 运动学解析

2.1 运动学逆解

所研究的平面二自由度并联机构结构简图，如图1所示。

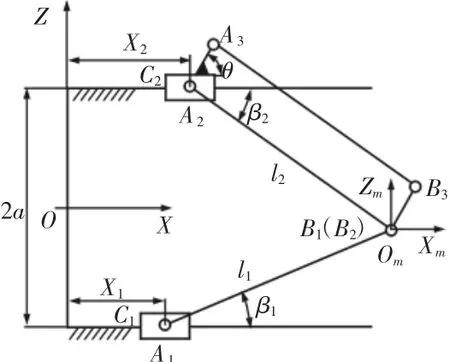
图1 并联机构结构简图Fig.1 Schematic Diagram of the Parallel Mechanism

它由杆 AiBi（i=1，2，3）、A2A3、B2B3和两个滑块 Ci，i=1，，2 组成。杆 A2A3、A3B3、B3B2、A2B2组成平行四边形结构，其中杆 A2A3与滑块C2固连。该机构中采用平行四边形结构使得动平台（固连于Bi，i=1，2点）的姿态保持不变，也增强了该机构的横向承载能力。当两滑块由电机驱动在导轨上做直线往复运动时，动平台实现两自由度的运动。

建立坐标系，如图1所示。定平台坐标系为ΣO-XZ，动平台坐标系为ΣOm-XmZm，其坐标原点Om在复合铰链的中心，两平行导轨间的距离为2a，杆长l1=l2=l。

在坐标系ΣO-XZ 下，设 Om点的坐标为（x，z），Ai点的坐标为（xi，zi），i=1，2，zi=（-1）ia。

根据几何关系可得：

式中：i=1，2，βi—杆 AiBi与 X 轴的夹角。

联立式（1）、式（2）可得该机构的约束方程为：

容易求得该并联机构的逆解为：

由于并联机构在滑块的右侧，从而式（5）、式（6）中取“-”号。

2.2 雅克比矩阵

式（1），式（2）对时间求导数可得：

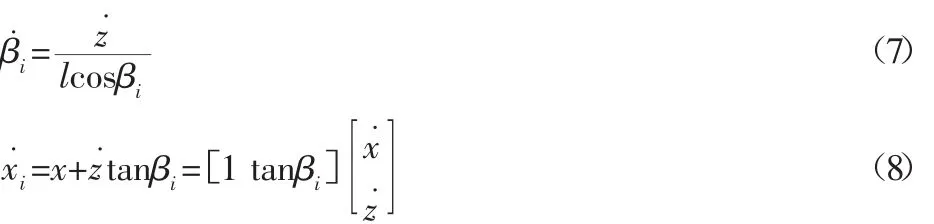
从而可得到该并联机构的雅克比矩阵为：

2.3 速度及加速度分析

设动平台参考点的速度矢量为：

从而容易获得滑块的运动速度为：

由式（7），式（8）对时间求导数可得：

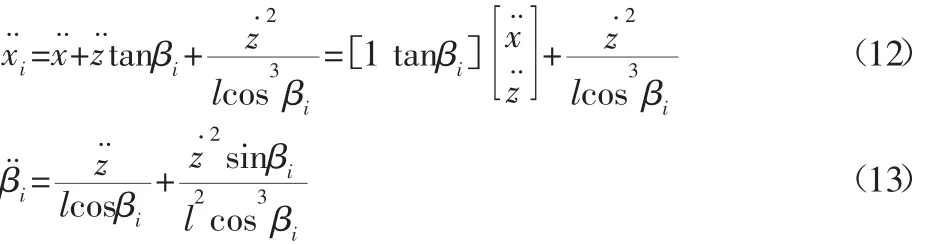
设动平台参考点的加速度矢量为：

从而各个滑块的加速度为：

2.4 偏速度矩阵和偏角速度矩阵

（1）对于滑块A1偏速度矩阵为：

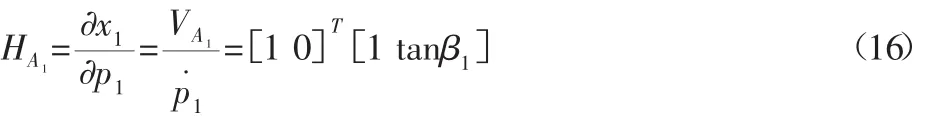
因滑块A1只有直线移动，没有转动，故偏角速度矩阵为：

（2）对于滑块A2偏速度矩阵为：

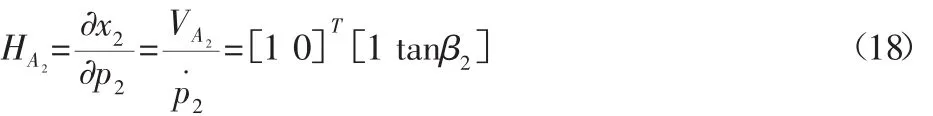
因滑块A2只有直线移动，没有转动，故偏角速度矩阵为：

（3）对于杆 li，（i=1，2），偏速度矩阵为：

偏角速度矩阵为：

（4）对于动平台偏速度矩阵为：

偏角速度矩阵为：

3 动力学方程建立

3.1 惯性力和惯性力矩分析

（1）对于滑块A（ii=1，2），其惯性力和惯性力矩分别为：

（2）对于连杆AiB（ii=1，2），其惯性力和惯性力矩分别为：

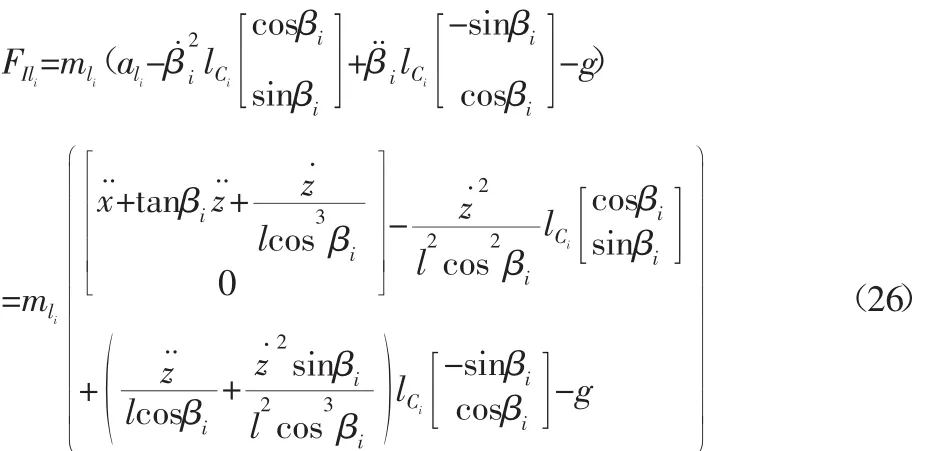
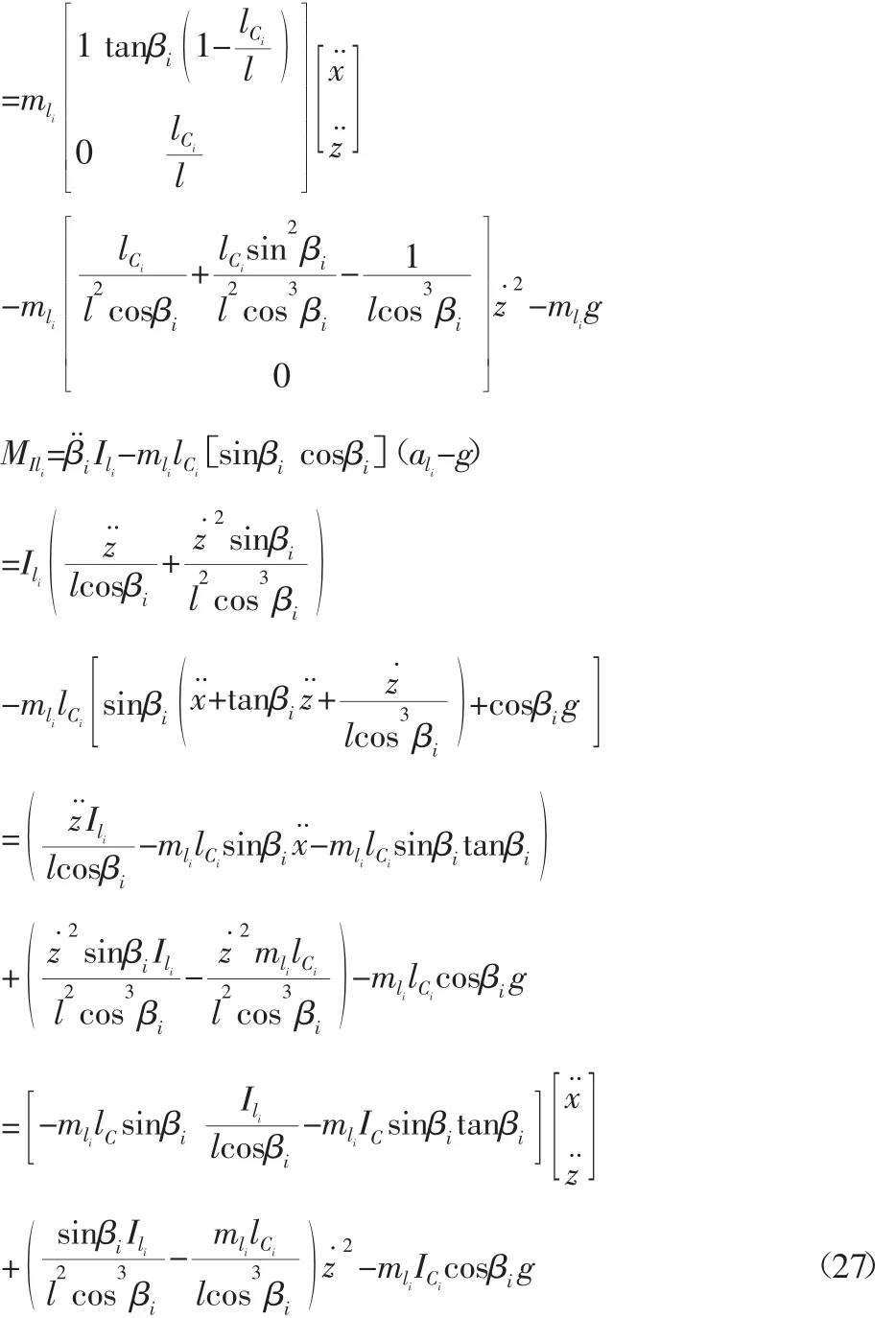
式中：lci—杆质心到转动副中心的距离；

Ili—杆对转动中心的转动惯量。

由于连杆A3B3和连杆A2B2具有相同的运动速度，且结构特征相同，因此连杆A3B3所受惯性力和惯性力矩与连杆A2B2相同。

（3）动平台处的惯性力及惯性力矩为：

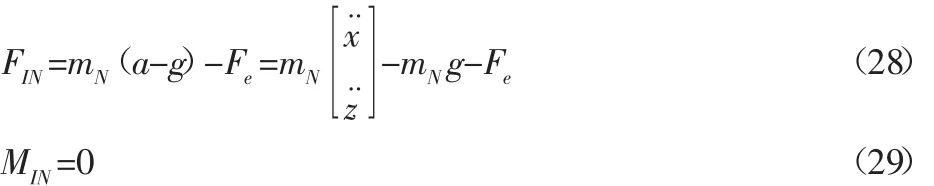
式中：mN—动平台的质量。

3.2 动力学方程建立

根据前文推导的偏速度、偏角速度以及惯性力和惯性力矩，由凯恩方程可得该机构的动力学方程为：

其中，τ=［τ1τ2］T

式中：τ1，τ2—作用于滑块 A1，A2上的驱动力。

整理后可得：

4 算例

设并联机构的结构参数为：mA1=1.65kg，mA2=2.70kg，ml1=ml2=ml3=3.33kg，mN=11.90kg，a=0.214m，l1=l2=l3=0.447m，Il1=Il2=Il3=0.022kg/m2，外载荷F=［200200］N。通过Matlab编程以及ADAMS仿真相结合的方法考核其正确性。

若动平台参考点在XZ平面内沿Z方向以速度v=0.03m/s从点（0.495，0.09）运动到点（0.495，-0.9）。根据动力学模型，分别利用Matlab和ADAMS软件得到动平台在外载荷F作用下所需驱动力的变化曲线，如图2所示。

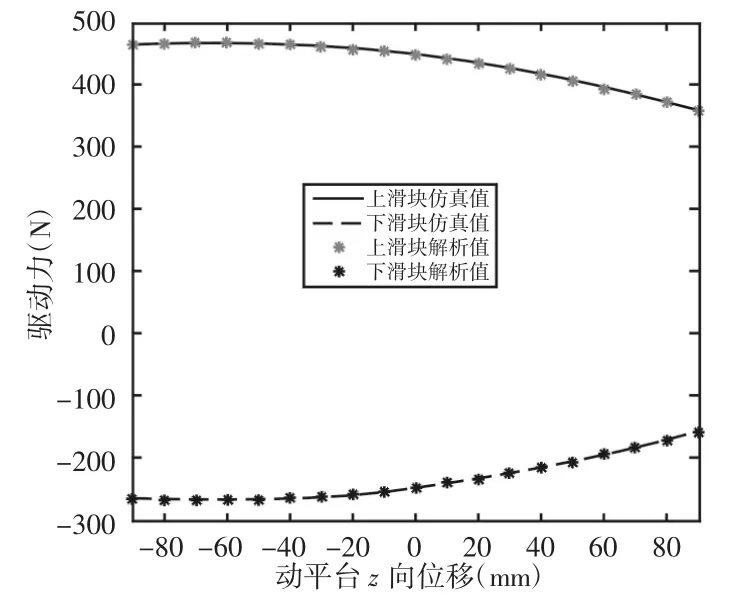
图2 Matlab和ADAMS仿真结果对比Fig.2 Comparison of Simulation Results about Matlab and ADAMS

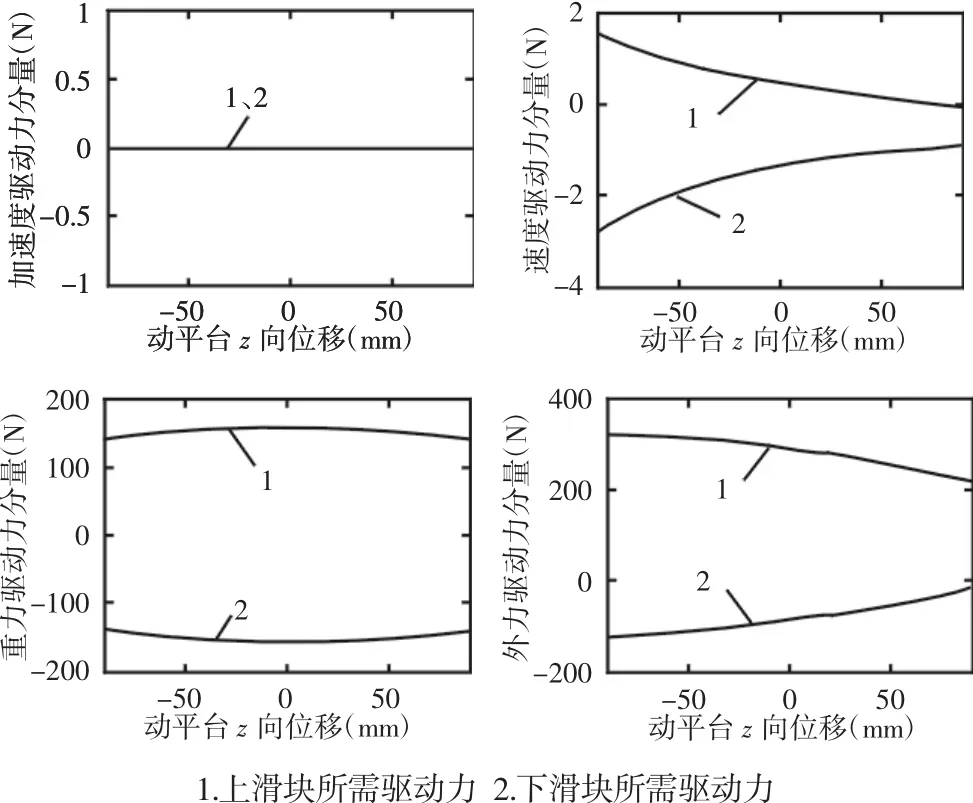
图3 动力学方程中各项驱动力分量（v=0.03m/s）Fig.3 The Driving Force Components in the Dynamical Equation（v=0.03m/s）

图4 不同加速度下克服惯性力所需驱动力分量Fig.4 The Driving Force Components Required to Overcome Inertia Force in Different Accelerated Velocities

图中：曲线1—a=10m/s2时克服惯性力所需驱动力分量；

曲线2—a=1m/s2时克服惯性力所需驱动力分量；

曲线3—a=0.1m/s2时克服惯性力所需驱动力分量。

由图2可以看出，用Matlab编程计算的结果与ADAMS虚拟仿真的结果基本一致，证明了所建立动力学模型的正确性。

由动力学模型可以看出，机构运动所需的驱动力要克服四部分的力分量，即为惯性力的驱动力分量、向心力和科氏力的驱动力分量、重力驱动力分量以及外载荷的驱动力分量。在上述运动条件下，动力学模型各驱动力分量，如图3所示。从图3中可以看出，当机构速度v=0.03m/s时，加速度驱动力分量和速度驱动力分量的作用并不明显，基本上是可以忽略的，此时驱动力主要体现在克服重力以及外载荷方面。但当机构以较高速度较高加速度运动时，机构的动力学特性将显著增强。不同加速度条件下上下滑块的驱动力分量，如图4所示。由图可以看出，随着机构加速度的增大，惯性力的驱动力分量显著增大。不同运动速度条件下上下滑块的驱动力分量。由图可以看出，随着机构速度的变大，向心力和科氏力的驱动力分量显著增大，如图5所示。