端面微造型机械密封的数值模拟与实验研究

郝木明，韩 婕，王赟磊，徐鲁帅

（中国石油大学（华东）密封技术研究所，山东 青岛 266555）

1 引言

目前，石油化工行业对机械密封的使用要求越来越高，对机械密封的性能提出了更高要求。由于使用工况更加苛刻，加剧了机械密封端面的磨损，降低了机械密封的使用寿命和安全性，因此需要提高机械密封的润滑性能。端面微造型机械密封通过激光技术改变端面形态达到减小端面间摩擦的效果，从而提高密封的润滑特性。端面微造型机械密封已在许多领域得到广泛的应用，文献[1-2]利用解析法研究了微造型端面的密封性能，并得到了动压系数、压力分布和泄漏率；随后[3-4]又建立了半球型微孔和圆柱型微孔的端面机械密封几何模型，求解了液膜的压力分布及开启力等性能参数，并分析了动静压效应与微孔效应之间的关系；文献[5-6]对LST-MS的磨损性能进行了系统实验，发现其摩擦系数低于传统机械密封；文献[7-8]探究了孔型排列方式、工作参数和结构参数等对端面密封性能的影响规律。研究者大都研究径向排列的微造型槽，鉴于螺旋槽液膜密封[9-10]具有承载能力好，泄漏量低等特点，基于流体质量守恒模型，以沿螺旋线方向排列的端面微造型机械密封流体膜为研究对象建立了物理模型。考虑了几何参数和工况参数对端面间液膜润滑性能的影响，进而分析了参数对密封性能的影响规律，为后续开展相关实验提供理论参考。

2 数学模型

2.1 几何模型

图1 端面微造型机械密封液膜模型Fig.1 Micro-Texture Mechanical Seal Liquid Film Model

机械密封端面微造型液膜的几何示意图，如图1所示。圆柱形微造型沿螺旋线方向分布。选取沿螺旋线方向排列的一列微造型为单周期液膜模型进行研究。

选取水为模拟介质，具体密封端面几何参数，如表1所示。

表1 密封端面几何参数Tab.1 Geometry Parameters of Seal Face

2.2 网格划分及边界条件

由于所建立的微造型液膜模型在厚度方向是微米数量级，无法对网格进行直接划分，因此，采用了将槽区与非槽区分区画网格的方法以保证网格的精度。由于微造型液膜长宽尺寸为毫米级，而液膜厚度、微造型深度属于微米级，故涉及跨尺度网格划分问题。对此，采用统一网格划分加局部网格加密的方法。将微造型密封环的内径、外径分别设置为压力入口和压力出口边界条件，将计算域的左、右堰区的竖直面定义为周期边界条件；静环为静止元件，将静环表面设置为静止；动环为旋转元件，将旋转速度赋给动环表面；其它边界默认为壁面边界条件。

2.3 控制方程

为了便于计算，忽略一些对研究重点影响较小的因素，作如下基本假设：（1）密封介质为粘性不可压缩流体；（2）不计重力；（3）密封表面无相对滑动；（4）密封表面为刚性端面；（5）润滑层的热状态为等温状态；（6）介质的流动过程为稳态。采用连续性方程描述流动过程中流体质量的性质[11]，直角坐标系下的连续性方程表示为：

式中：u、v、w—速度；ρ—流体密度。

2.4 性能参数

2.4.1 开启力

密封端面开启力是指作用在密封端面上液膜压力的总和，对端面液膜压力场积分得：

式中：Ω—整个计算域；p—液膜压力；r—径向坐标。

2.4.2 泄漏量

泄漏量作为决定密封性能的重要参数，可用下式进行计算：

式中：h—膜厚。

2.4.3 摩擦扭矩

为了计算相应的摩擦扭矩，必须先求得端面上对应的摩擦力。将该摩擦近似认为纯流体摩擦，摩擦力通过下式进行计算：

式中：τ—液膜剪应力；d A—面积微元。

忽略压力梯度影响，由牛顿粘性剪切定律得：

式中：U—切向线速度；μ—液体的动力粘度。

端面的摩擦扭矩可近似为：

3 模拟结果与讨论

机械密封端面微造型液膜压力分布云图，如图2所示。当动环转动时，高压侧的流体泵入槽区，由于动环的转动在动环和静环表面形成流体膜，在切向剪切力的作用下流体在槽区内流动，由于每一个微造型孔都相当于一个微动力滑动轴承[12]，会在微造型上方及其周边产生流体动压力，即形成流体动压效应。在槽区和非槽区的收敛区域形成压力最高点，在槽区和非槽区的发散区压力迅速下降，形成压力最低点。

图2 单周期液膜压力云图Fig.2 Single Period Liquid Film Pressure Distribution

3.1 槽深对密封性能的影响

当槽区半径、非槽区深度以及螺旋角不变时，转速不同时端面微造型机械密封的密封性能参数随槽区深度的变化曲线，如图3所示。由图3可以看出，随着槽区深度的增加，开启力呈现出先增加后减小的趋势，rp＜2.5mm时，开启力随着槽区深度的增加而增加，当rp＞2.5mm时，流体动压效应增加的趋势小于槽区内流体静压的增加趋势，因此开启力减小；同样研究了转速对泄漏量的影响，随着槽区深度的增加，泄漏量呈现出缓慢增加的趋势。压差不同时端面微造型机械密封的密封性能参数随槽区深度的变化规律是：随着槽区深度的增加，在改变压差时泄漏量缓慢增加；随着槽区深度的改变，开启力在压差改变的情况下随着槽区深度的增加逐渐增加；同时，由结果可知，当槽区半径固定不变时，随着压差和转速的增加，泄漏量和开启力呈现增加趋势。

图3 槽区深度-开启力关系图Fig.3 Relationship of Groove Depth and Opening Force

3.2 槽区半径对密封性能的影响

当槽区深度、非槽区深度以及螺旋角不变时，转速不同时端面微造型机械密封的密封性能参数随槽区半径的变化曲线，如图4所示。由4图可知，转速固定不变时，随着槽区半径的增加泄漏量和开启力呈现逐渐减小的趋势；开启力逐渐变小是由于当槽区半径增加时，微造型之间的排列过于紧密，两个微造型之间的距离过小导致流体在槽阶梯收敛区还未充分增压就进入发散区开始降压，因此动压效应减弱，开启力减小。当转速小于3000r/min时，随着槽区半径的增加，泄漏量的减小趋势缓慢，而转速大于3000r/min时，泄漏量的减小趋势逐渐变大；固定槽区半径增加转速，开启力逐渐增大。转速、槽区半径一定压差不同时，随着压差的增加，泄漏量和开启力随之增加。

图4 槽区半径-泄漏量关系图Fig.4 Relationship of Groove Radius and Leakage

3.3 非槽区深对密封性能的影响

当槽区深度、槽区半径以及螺旋角不变时，压差和转速不同时端面微造型机械密封的密封性能参数随非槽区深度的变化曲线，如图5所示。由图5（a）可知，当压差＜0.2MPa时，随着槽区深度的增加，泄漏量的增加趋势缓慢，当压差＞0.2MPa时，泄漏量的增加趋势变大，当非槽区深度不变时，随着压差的增加泄漏量逐渐增加；由图5（b）可知，随着转速的增加，泄漏量先逐渐增加，当非槽区深度＞6μm时，增加趋势变缓慢；压差或非槽区深度中的任何一项增加，开启力会随着增加；随着非槽区深度的增加开启力增加，当转速大于4000r/min时开启力增加趋势变大。

图5 非槽区深度-开启力-泄漏量关系图Fig.5 Relationship of Non-Groove Radius，Opening Force and Leakage

3.4 螺旋角对密封性能的影响

当槽区深度、槽区半径以及非槽区深度不变时，转速不同时端面微造型机械密封的密封性能参数随微造型排列螺旋角的变化曲线，如图6所示。由图6可知，随着微造型所在螺旋线角度的变化，泄漏量和开启力会发生相应的变化，由图6（a）可知，在压差不变时，随着螺旋角的增加泄漏量逐渐减小；在压差变化的情况下，随着角度的增大，开启力虽然减小，但是减小趋势缓慢；由图6（b）可看出，在转速变化的情况下，随着角度的增大，开启力先逐渐减小，且当螺旋角为27°时开启力有最小值，后续随着角度增加开启力又呈现增加的趋势。

图6 螺旋角-开启力-泄漏量关系图Fig.6 Relationship of Spiral Angle，Opening Force and Leakage

4 实验结果及讨论

4.1 实验目的和方法

图7 转矩转速测量仪Fig.7 Tachometer Torquemeter

机械密封动、静环端面间的摩擦扭矩影响着密封运转时的端面磨损情况及摩擦热等性能参数，对机械密封的稳定运转有重要的影响。为了验证模拟结果的准确性，采用转矩转速测量仪对端面微造型机械密封的摩擦扭矩进行了实验测量，如图7所示。并与模拟值进行了对比，采用的实验装置，如图8所示。

图8 实验装置图Fig.8 Experimental Device Figure

4.2 实验结果

压差和转速对摩擦扭矩的影响，如图9所示。由图9（a）和图9（b）可知，随着压差或转速的增加，端面微造型机械密封的摩擦扭矩逐渐增大，且在理论研究中，随着压差和转速的增加摩擦扭矩的增长率小于实验研究中摩擦扭矩的增长率，这是由于实际工况中，密封副表面的粗糙度不可忽略。

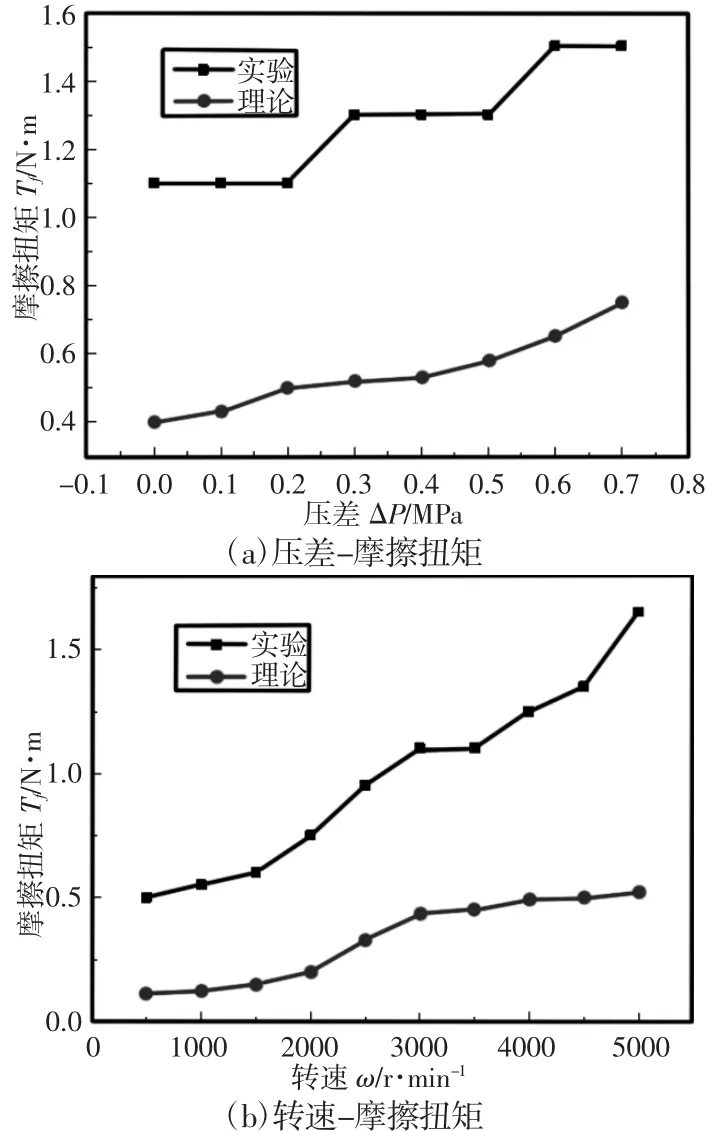
图9 压差-转速-摩擦扭矩关系图Fig.9 Relationship of Pressure Differentials，Rotation Rate and Friction Torque

5 结论

（1）槽区深度、槽区半径、非槽区深度以及螺旋角等结构参数对端面微造型机械密封的开启力、泄漏量有影响，结构参数应存在最佳值，并未考虑，后续应进一步研究；转速、压差对端面微造型机械密封的开启力、泄漏量的影响也不能忽略，在使用中应选择合理的操作参数；（2）实验所得摩擦扭矩变化规律与模拟所得摩擦扭矩变化规律基本吻合，但由于摩擦副的粗糙度等实际中不可忽略因素的存在，实验值大于模拟值。