多面体外接球问题的“模式化”解题策略

2018-10-22福建省惠安荷山中学杨春元

中学数学杂志 2018年19期

☉福建省惠安荷山中学杨春元

2018年《普通高等学校招生全国统一考试大纲》指出：“空间想象力是空间形式的观察、分析和抽象的能力，主要表现为识图、画图和对图形的想象能力.”“对图形的想象包括有图想图和无图想图两种，是空间想象能力高层次的标志”［1］.立体几何是考查空间想象能力的主要载体，多面体外接球问题能全方位、多角度、深层次考查空间想象能力，是高考试题的难点之一，这类问题由于不易画图而变得抽象难解，需要有图想图或无图想图.本文通过具体案例谈谈这类问题的“模式化”处理策略.

一、知识理解

1.多面体外接球问题

多面体的每个顶点都在同一个球面上，那么这个多面体是球的内接多面体，球是多面体的外接球，多面体的每个顶点到球心的距离都等于半径，多面体每个面所在的平面与外接球的截面是每个面的外接圆.研究多面体的外接球问题，既要运用多面体的知识，又要运用球的知识，还要特别注意多面体的有关几何元素与球的半径和球心之间的联系.

对称几何体中心为几何体外接球球心：

（1）长方体外接球球心是其体对角线中点，半径为体对角线长的一半.

（2）直三棱柱的外接球的球心是上下底面外心连线的中点，半径可在以球心、底面圆心、底面一个顶点为顶点组成的直角三角形中求解.

（3）正棱锥的外接球球心在其高上，半径可在以球心、底面中心、底面一个顶点为顶点组成的直角三角形中求解.

2.“模式化”解题策略

多面体外接球问题的核心是寻找球心求半径.可构造长方体确定球心的有以下情形：正四面体、同一个顶点上的三条棱两两垂直的四面体、对棱相等的三棱锥、四个面都是直角三角形的三棱锥、棱锥含有线面垂直关系（或可构造直三棱柱）.

确定球心求解半径可以分三步：

（1）判断几何体是否为对称几何体（长方体、直三棱柱、正棱锥）、判断几何体是否可以补成长方体或直三棱柱；

（2）找几何体的外接球球心（球心在过几何体两个面外接圆圆心的面的垂线交点处）；

（3）运算求解外接球的半径.

二、问题辨析

例1（2017年福建省质检理科10）空间四边形ABCD的四个顶点都在同一个球面上，E，F分别是AB，CD的中点，且EF⊥AB，EF⊥CD.若AB=8，CD=EF=4，则该球的半径等于（）.

分析：求解多面体外接球表面积关键是确定球心和半径，找球心求半径从理解几何体入手，根据题意作出图1.由已知条件，可得空间四边形ABCD关于平面ABF对称，也关于平面CDE对称，所以球心O在线段EF上.

解：球心O，设OF=x，则OE=4-x，空间四边形ABCD中，E，F分别是AB，CD的中点，且EF⊥AB，EF⊥CD.AB=8，CD=EF=4.

在Rt△OCF中，OC2=OF2+CF2=x2+22；

在Rt△OBE中，OB2=OE2+BE2=（4-x）2+42.

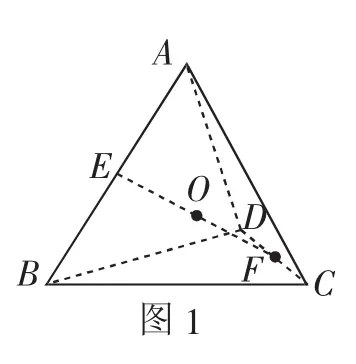
由OB=OC，得x2+22=（4-x）2+42，所以

小结：解决多面体外接球问题，首先要研究多面体，空间四边形ABCD是轴对称图形，空间四边形ABCD外接球的球心在对称轴上，利用外接球球心到多边形每个顶点距离都等于半径列方程求解.

例2已知，三棱锥P-ABC中，PA⊥平面ABC，PA=1，则三棱锥P-ABC外接球的表面积为______.

分析：求解多面体外接球表面积关键是确定球心和半径，找球心求半径从理解几何体入手.本题为三棱锥P-ABC，PA⊥平面ABC，可以构造长方体确定球心，进而求解半径.

解：在△ABC中，AB=2，AC=∠BAC=30°.

由余弦定理BC2=AB2+AC2-2AB·AC·cos∠BAC=1，所以BC=1.

所以AB2=AC2+BC2，所以∠ACB=90°.

如图2，构造长方体，所以PB为外接球的直径.

在Rt△PAB中，PB2=PA2+AB2=5，所以

所以三棱锥P-ABC外接球的表面积为S=5π.

小结：解决多面体外接球问题，首先要研究多面体，四个面都是直角三角形的三棱锥，可以构造长方体确定球心求得半径.

例3（2017年福建省单科质检理科16）在三棱锥S-ABC中，△ABC是边长为3的等边三角形二面角S-AB-C的大小为120°，则此三棱锥的外接球的表面积为______.

分析：求解多面体外接球表面积关键是确定球心和半径，找球心求半径从理解几何体入手，根据题意作出图3，易得SA⊥AB，取BA，BS中点D，E，得∠CDE为二面角S-AB-C的平面角，△SAB是以BS为斜边的直角三角形，△ABC为等边三角形，则三棱锥S-ABC的外接球球心是过点E的平面SAB垂线与过点I的平面ABC（点I为等边△ABC的外心）的垂线的交点O.

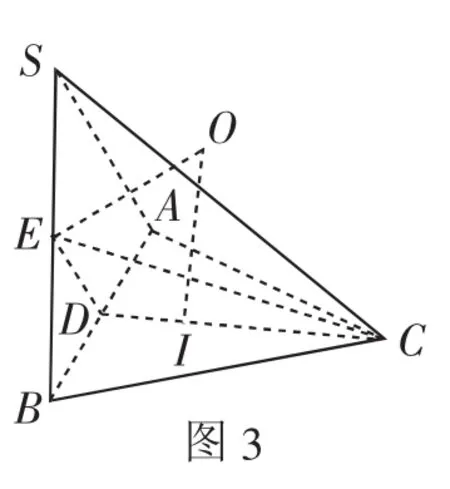
所以SB2=AB2+SA2，所以∠SAB=90°.

取BA，BS中点D，E，

连接DE、DC，得DE⊥AB，DC⊥AB.

所以∠CDE为二面角S-AB-C的平面角.

所以∠CDE=120°.

所以△SAB是以BS为斜边的直角三角形，△ABC是等边三角形.

三棱锥S-ABC外接球的球心是过点E的平面SAB的垂线与过点I的平面ABC（点I为等边△ABC的外心）的垂线的交点O.

在平面四边形OEDI中，∠OED=∠OID=90°，DE=DI，∠DEI=120°.

所以Rt△ODI和Rt△ODE全等.

在Rt△ODE中，∠OED=90°，∠ODE=60°，DE=

三棱锥S-ABC的外接球半径为OB.

所以三棱锥SABC外接球的表面积为21π.

小结：解决多面体外接球问题，首先要研究多面体，直角三角形的外接圆圆心是斜边上的中点，正三角形外接圆圆心是正三角形中心，多面体外接球球心在过几何体两个面外接圆圆心的垂线交点处.

三、拓展思考

球体是完美的对称几何体.若几何体是中心对称图形，则几何体的中心即为外接球球心；若几何体是轴对称图形，则外接球球心在几何体的对称轴上；若几何体是平面对称图形，则外接球球心在几何体的对称平面上.若几何体不是对称图形，几何体能补成长方体或直三棱柱则外接球球心可找到.否则，球心在过几何体两个面外接圆圆心的垂线交点处.

确定了外接球球心，我们可综合运用平几、解三角形有关知识求解外接球的半径，最后问题得解.