极限思想的解题应用与思考

☉江苏省靖江市第一高级中学 王国军

“极限”是数学中较为重要的概念，在数学的众多问题中都有渗透，对于该类问题的分析可以采用极限思想，从趋近性角度来洞察问题的极端状态，探索解题思路，下面将对极限思想进行解题探讨.

一、解题分析与应用

1.函数问题

函数是高中阶段最为重要的内容，也是其他知识学习的基础，利用极限思维研究函数是数学中较为常用的一种方式，在分析函数的变化趋势、取值范围、单调区间等方面有着极好的便利性，是解决问题的重要思想方法.

例1已知函数f（x）=（x-2）ex-a（x-1）2（a＞0），试分析f（x）的零点个数.

分析：分析函数f（x）的零点个数，实际上就是分析函数的变化趋势，需要绘制函数的图像，可以借助函数的导函数，利用极限思想判定x→+∞和x→-∞时的变化趋势，然后确定零点个数.

解：令（x-2）ex+a（x-1）2=0，则（x-2）ex=-a（x-1）2.令g（x）=（x-2）ex，g′（x）=（x-1）ex.当x∈（1，+∞）时，g′（x）＞0，g（x）单调递增；当x∈（-∞，1）时，g′（x）＜0，g（x）单调递减，且g（1）=-e＜0.

令h（x）=-a（x-1）2，由于a＞0，则函数h（x）的图像开口向下，h（1）=0，则其顶点为（1，0）.

分析可知当x→-∞时，g（x）→0，即极限为0，h（x）→-∞；当x→+∞时，g（x）→+∞，h（x）→-∞，如图1所示，由于a＞0时，函数g（x）和h（x）的图像必有两个交点，则原函数f（x）的零点个数为2.

函数的曲线变化反应的是因变量与自变量之间的联系，其中隐含着较为重要的函数性质，而函数的这种独有的变化实际上就是数学上的极限，即曲线的趋向性.利用极限思想求解时需要借助导函数，构建函数研究的模型，然后从极限角度分析曲线的趋向，函数问题的形式是多样的，但从函数的性质出发，挖掘曲线的变化信息是最本质的解法.首先在区间［0，1］上取两组均匀分布的随机数：x1，x2，x3，…，xN和y1，y2，y3，…，yN，然后将其组成N个点（xi，yi）（i=1，2，3，…，N），最后从中抽取出满足yi≤f（xi）（i=1，2，3，…，N）的点，设点数为N1，由此就可以估算出积分

2.概率问题

概率反映的是试验结果出现的一种可能性，是一种试验频率，一般随着试验次数的增多、统计量的加大，频率会越发准确地还原事件的真实情况，因此是一个抽象的数学概念，其本身就渗透着极限思想，利用极限思想来研究概率问题更贴近概率本源.

例2y=f（x）是区间［0，1］上的连续函数，并且在区间上始终满足0≤f（x）≤1，现采用随机模拟的方式来估算积分则其近似值为多少？

分析：根据题目信息可知，x∈［0，1］，y∈［0，1］，由极限思想可以将其理解为N个点（xi，yi）组成了一个面积为1的区域，估算积分的值需要从区域中提取出满足条件的点，则相当于从中提取一块面积，计算面积的比率.

解：N个点（xi，yi）组成了一块面积为1的区域，而表示的是该区域的曲边梯形围城的面积，如

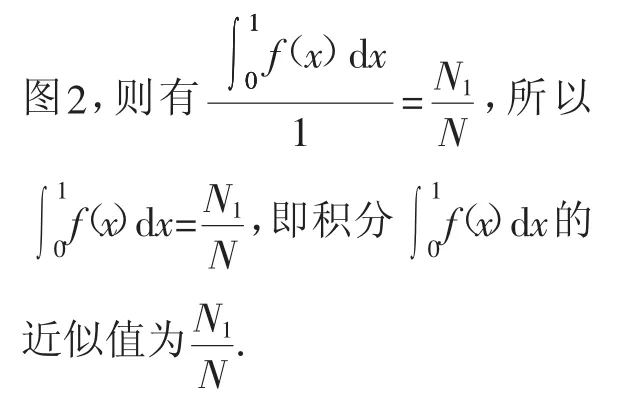
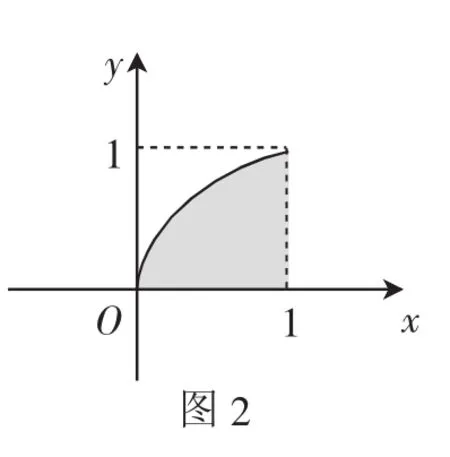
极限思想在概率研究中有着极为重要的地位，是其基础理论建立的重要思想.微积分是高等数学的内容，在高中阶段则可以采用极限的思想对其加以描述，即从区域面积角度构建模型.另外，极限思想可以还原概率的抽象过程，假设出概率问题的极端情形，从而获得解决问题的有效方法，因此，极限思想是构建创造性解题思路的指导思想.

3.立体几何问题

极限思想在立体几何中的应用主要体现在对几何形状、面积、角度、长度的特定描述，可以从直观角度完美呈现问题研究的模型.几何求解中的特值法和假设法，常通过设定几何图形的相关参数来构建模型，其中就渗透着数学的极限思想，是极限思维的一种应用.

例3如图3所示，圆的直径为AB，C是圆上的一点，PA垂直圆所处的平面，DE垂直平分PB，交AB于点D，交PB于点E，已知PA=AC，PC=CB.如果点Q位于线段PA上，分析是否存在一点Q，使得PB与平面QCD成45°角？

分析：本题目求满足PB与平面QCD成45°角时点P的位置，实际上为几何动点问题，设PB与平面QCD所成角为θ，二面角Q-CD-E的平面角为α，则两者之间存在如下关系：随着点Q的移动，α的大小也会发生变化，可以使用极限思想，考虑点Q的极端位置P和A两点处的情形，从而判断θ为45°的可能性，则问题的关键是首先确定二面角Q-CD-E的平面角，可以利用立体几何知识确定.

解：分析可知，CE⊥PB，DE⊥PB，则PB⊥平面CDE，有CD⊥PB.又因PA垂直底面圆，则PA⊥CD.由可知CD⊥平面PAB，则有CD⊥DE，CD⊥DQ，所以二面角Q-CD-E的平面角为∠EDQ.

设PB与平面QCD所成角为θ，二面角Q-CD-E的平面角∠EDQ为α，则有分析可知当点Q从点P移向点A的过程中，α是逐渐增大的过程，位于点P、A时处于极端位置.

在立体几何中，点的运动会显著改变几何形状，进而影响几何的性质，使得角度、线段长度和几何面积等发生变化，虽然这种变化的过程是复杂的，但一般存在着一定的数学规律，求解时就可以首先建立一个问题研究的模型，利用极限思想，设定几何的特定情形来针对性研究，从而获得具有说服力的结论.

二、思想解读与教学

极限思想是以所研究内容为载体，远高于知识内容的一种策略性指导思想.因此，极限思想是基于认知基础上形成的，是对相关事物本源的深度挖掘，是对概念的一种本质认识，利用极限思想可以更加逼真地还原事物的本来面目.

高中数学的很多内容都渗透着极限思想，简单到代数的数集，图形中线的延伸，复杂到函数的渐近线、连续、极值等.另外数学的很多方法也都涉及极限思想，如常用的数学归纳法就是极限指导下的结论概括，球的体积与面积公式的推导所使用的就是极限思想.学习和使用极限思想不仅对于知识内容的掌握有着重要作用，对于拓展学生的数学思维同样有着重要意义.

教学中对于极限思想的渗透需要遵循一定的思维过程，要结合特定的情形逐步引导学生完成从感性认识到理性思考的认知过渡.首先需要建立在学生认知冲突的基础之上，使学生发现用已学知识难以解决问题，不能准确认识数学的概念或符号，如数学中的无穷大、无穷小，可适时地引入“∞”.然后需要从知识联系性角度完成知识的过渡，使学生深度认识到极限思想理解数学知识的重要意义，如立体几何中的棱锥的侧面积，可以采用初中数学展开图的方式，建立几何求解的相关公式.极限思想最为关键的阶段是对思想的理性论证，应立足于教材内容，从规律总结、结论探究角度进行，必须遵循科学的论证原则，如sinx和x的大小比较，可以采用数学上的特值法，也可以利用单位圆来直观比较.教学中使用“认知冲突——知识过渡——理性论证”的模式更能使学生深刻理解极限的思想方法.

总之，极限的思想方法是中学阶段十分重要的内容，利用极限思想不仅可以更为准确地描述数学的概念公式，还可以广泛应用于数学解题中，优化解题过程，降低思维难度.极限思想是对事物本质的一种趋近，学习和使用极限思想具有重要的意义，高中阶段对于该思想的教学应遵循科学的模式，以提高思想教学效率.