高中数学教学中“证伪”思想运用的思考

☉江苏省宜兴第一中学 陈 达

概念与正确命题的逻辑体系是数学在人们面前的最终展现，由此可见，严密论证在数学学科中是当仁不让的中心，不过，我们也不难发现围绕猜想性命题的数学活动始终指向了提出证明和进行“证伪”这两个方向.数理逻辑与数学方法论从不同角度对前一个方向都进行了大量的研究并获得了很多成果，相对而言，后一个方向的研究却是比较鲜见的.事实上，“证伪”这一否定性思维能够有效帮助学生科学超越自身并因此获得新的生长点与突破口.

一、“证伪”思想的概述

1.来源和特点

证伪主义科学观是英国哲学家卡尔·波普尔提出并发展起来的，他认为“提出假说——证伪——再提出假说——再证伪……”这一不断循环的过程正是科学接近真理的道路，不仅如此，他还归纳了证伪主义的两个优点：（1）经验具备一定的个别性，但科学理论却是一个全称判断的准确表达，经验可以用于科学理论的证伪；（2）证伪主义使人相信所有的科学都是一种猜测与假说并能避免对错误理论的辩护与教条.

2.“证伪”思想在解题中的运用

人们大胆提出假说与猜测并寻找和这一假说不符合的事例的方法就是证伪主义经常采用的试错法.“证伪”思想运用于数学解题中一般遵循下图中的流程.

二、“证伪”思想的运用价值

1.促进学生基本概念的掌握

反映数学对象本质属性的概念是导出数学定理与法则的逻辑基础，如何提升概念教学的效果是所有数学教师都非常关注的难题，数学概念的“证伪”进程对于概念掌握具有积极的意义.

案例1：概率的学习.

教师在概率这一概念的教学中可以举出相关内容的正例以及容易与这一概念产生混淆的概念，使学生在进行“证伪”过程中对概念外延的关键词形成更好的理解.比如：①所有频率的平均值就是概率值；②当实验次数够大时，所有频率的平均值就是概率值；③当实验次数够大时，所有频率的近似值就是概率值；④当次数n→+∞时，频率趋近的常数就是概率值.引导学生在这些实例中进行辨析、比较，并因此对概念、概念的适用对象与范围形成真正的理解.

2.促进学生推理能力的提高

人们在学习与生活中经常会使用推理和证明这两个基本的思维方式，“证伪”思想的应用能够更好地锻炼学生的推理能力.

案例2：运用数学归纳法证明任何两个正整数都相等.

证明：设An表示命题：若a、b为任意两个正整数，令max（a，b）=n，则a=b.

（1）当n=1时，命题A是真的，因若max（a，b）=1，a、b又均为正整数，故最大值是1，只能是a=b=1.

（2）假设命题Ak为真，设max（a，b）=k时，a=b为真（a、b为正整数），

考察两个整数：α=a-1，β=b-1， ①

由于式子max（a，b）=k+1， ②

与max（a-1，b-1）=k， ③

明显是等价的，即如果a、b的最大值是（k+1）的话，则（a-1）和（b-1）的最大值明显就是k.因此，由①式得max（α，β）=max（a-1，b-1）=k.

而根据归纳法假设Ak为真，则得α=β.即（a-1）=（b-1），故a=B.但因为②和③的等价性，则证得Ak+1为真.

由（1）（2）可知，对一切自然数r，Ar为真，对特殊的n，An为真，因此有a=b.很多学生并不能一眼发现其中隐匿的问题，但也明白其中是有差错的，经过仔细检查与讨论之后很快可以发现假设α=a-1、β=b-1时，α、β是包含零的，但要证明的起始数为1，问题也就凸显出来了.

3.帮助学生校正问题的分析

波利亚强调过中学数学教学就是加强解题训练这一观点，高中数学新课标也明确提出了数学教学应培养学生分析、解决问题的能力这一具体的要求.

案例3：二次函数（fx）=ax2+bx+c的图像经过点（-1，0），且对所有实数x均成立，求函数（fx）的解析式.

参考答案：对x∈R，均有故可设x、为数轴上的三点，（fx）分x所成的比是λ（λ≥0），根据定比分点公式可得：

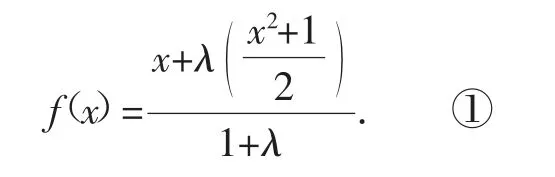
一部分学生在课余仍对此题的新颖思路惊艳不已并产生了这一解法是否为此类问题的普遍解法的思考.笔者趁机引导学生对此进行了讨论，大家很快发现这一解题具备一定的合理成分，最后的答案也与题目中的条件相吻合，不过并不能代表此题只有②这一个解，相对来说，有一定的失根风险，此题的唯一解也只是一种巧合.

笔者适时引导学生尝试运用反例来对这一问题进行了验证，具体如下：

反例：二次函数（fx）=ax2+bx+c的图像经过点（-1，0），且对所有实数x均成立，求函数（fx）的解析式.

评注：②式很明显也是这一反例的解，不过类似的定比分点却难以求出.

因为根据上述解法可解得此题的答案为：

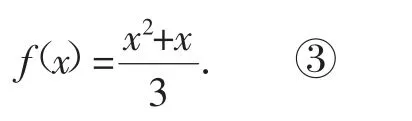
②、③两式虽有不同但却都符合题意，不仅如此，满足条件的解还远远不止这两个.另外，如果将反例中的点（-1，0）改成（1，1），运用之前的解法是无法求出（fx）的，但②式明显是符合条件的，由此可见，上述解法在逻辑上是存在一定漏洞的.

4.催化学生的思维创新

数学教学自然包含培养学生创新思维这一重要的课题，因此，教师在实际教学中引导学生发现新知并鼓励创新也就变得尤为重要了，创设情境并引导学生进行探索性问题训练、提出命题、改变命题、尝试多种解题都是促进学生发现新知并获得思维创新锻炼的良好途径，“证伪”思想在锻炼学生创新思维的过程中也是极有意义的.

案例4：已知数列{an}为等比数列，Sn为其前n项之和，求证：S7，S14-S7，S21-S14成等比数列.

这是一节公开课上的例题，执教老师在此题的解决上运用了两种方法并对学生提问：“能不能不改变题目的前提并将其一般化，问：如果k∈N*，Sk，S2k-Sk，S3k-S2k是否成等比数列呢？”

大部分的学生面对这一问题毫不犹豫：“成立！”

执教老师：“如何解决这一问题呢？”

有学生踊跃举手，但执教老师感觉上课的主题还未接触，唯恐学生的解题会耽误课堂教学的进程而稍有犹豫，但很快考虑到学生积极性与探求欲望的保护便请该学生进行了解题描述.

该生表达比较清晰：“我认为这三项不一定能成等比数列，比如以下数列：1，-1，1，-1，1，-1，…是等比数列，不过S2=S4-S2=S6-S4=0却不是等比数列！”

执教老师和学生对该生的发言都很惊讶，教师对于该生的精彩发言进行了鼓励并引导学生尝试反例的列举，学生经过一定的讨论之后仍未有所收获，执教老师于是给出了自己的想法：“老师倒是有一个反例，不过同学们的知识水平或许有点跟不上，不过有兴趣的同学在课后可以尝试着琢磨琢磨.”例子如下：

等比数列{an}中，首项a1=1，公比但S7=S14-S7=S21-S14=0，因此，此时S7，S14-S7，S21-S14也不是等比数列.

总之，“证伪”思想在高中数学教学中的运用能够更好地促进学生对知识的探求，不过，也不是所有的数学学习都必须运用这一思想，教师在一些较难掌握、容易混淆、容易造成迷惑的数学知识的教学中可以将“证伪”思想的实践运用引进课堂，以促成学生更好地掌握知识.