70基于负超磁致伸缩效应电抗器减振新方法的研究

闫荣格，赵路娜,2，贲 彤， 周 杰

(1.省部共建电工装备可靠性与智能化国家重点实验室 河北工业大学 电气工程学院，天津 300130；2.国网山东菏泽供电公司，山东 菏泽 274000)

电抗器是电力系统中必不可少的电气设备，有限制短路电流，补偿系统无功功率以及与其他元件组成滤波电路的作用[1]，但其特殊的铁心结构使得其振动噪声比普通电力电抗器严重的多[2-3]，振动噪声不仅威胁电抗器的长期可靠运行，还造成噪声污染，因此对铁心电抗器的减振降噪有重要的现实意义。

目前，国内对变压器、电抗器的噪声抑制多集中在基础减振。特变电工集团[4]发明的三处压紧装置并采用铁心饼真空压力浇铸的方法。彭新宏等[5]采取加强油箱底部强度，增加千斤顶等措施。韩江桂等[6]提出增加基座的刚度，同时减小弹性联接的刚度。但这些都属于基础加固，并未从根源上降低电抗器的振动。Tong等[7-8]等研究了直流偏磁和阻尼效应对电抗器振动噪声的影响。丁登伟等[9]研究发现变压器振动信号的奇偶谐波能量比与电流有关，但并未采取相应的减振措施。Gao等[10-11]对气隙处采用硬度大的环氧树脂填充，达到降噪的效果。Ishikawa等[12]提出一种三角型电抗器，通过分散电磁力达到减振的效果，但制作工艺复杂。

本文在工况下对硅钢样片和负超磁致伸缩材料的磁特性进行测试，将实验得到的材料特性添加到电抗器模型。对电抗器施加不同载荷即单独考虑麦克斯韦力、磁致伸缩力及两者共同作用，建立电抗器电磁-机械耦合数值模型，用数值方法计算电抗器铁心的振动位移。负超磁致伸缩材料代替环氧玻璃板填充在气隙处，利用负超磁致伸缩材料产生的机械变形与电抗器本身的振动响应相互抵消的原理减小铁心振动。通过对比分析两种不同填充材料下电抗器的振动位移，验证该方法的有效性，为以后设计低振动的电工设备提供理论支持。

1 磁特性测量

本文首先利用激光磁致伸缩测量系统对硅钢片进行磁化特性及磁致伸缩特性测试，测试装置如图1所示。该装置工作原理为：激光器(工作频率为50 Hz，分辨率为10 nm/m)发射光束到反光片，反光片贴在测试样片可以自由伸缩的一端，样片另一端固定，且在样片长度方向施加磁场，此时样片产生磁致伸缩，反光片将光束反射回激光器，根据反射时间差得到检测样片的磁致伸缩形变量；同时，根据不同激励条件下，不同磁通密度幅值下磁滞回线顶点连线得到样片在不同激励条件下的磁化曲线。

图1 磁特性测量装置Fig.1 Magnetic characteristic measuring device

1.1 硅钢片的磁特性测量

本文按照2010年国际电工委员会公布的硅钢片的磁致伸缩特性测量IEC标准，对无取向硅钢片50WW470进行了测量，得到硅钢片的基本磁化曲线及磁致伸缩λ与磁场强度的关系，如图2所示。

1.2 NGMM的磁特性

本文采用的负超磁致伸缩材料Sm-Nd-Fe是一种在磁场的作用下产生巨大伸缩形变的智能材料，具有应变值高、磁导率较低、抗压能力强、抗拉能力弱的特点。在电抗器运行过程中负磁致伸缩材料始终受到的是相邻铁饼之间的挤压力，故不存在材料的脆性问题。图3为负超磁致伸缩材料的实物图，其磁化特性和磁致伸缩特性曲线如图4所示。

(a) 基本磁化曲线

(b) 磁致伸缩与磁场的关系

图3 负超磁致伸缩材料实物图Fig.3 Physical drawing of NGMM

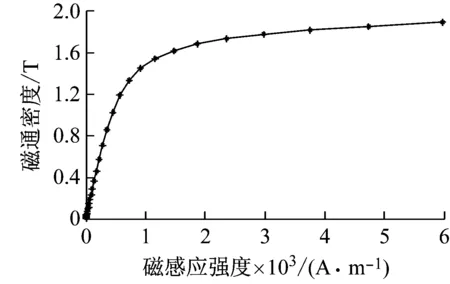
(a) 基本磁化曲线

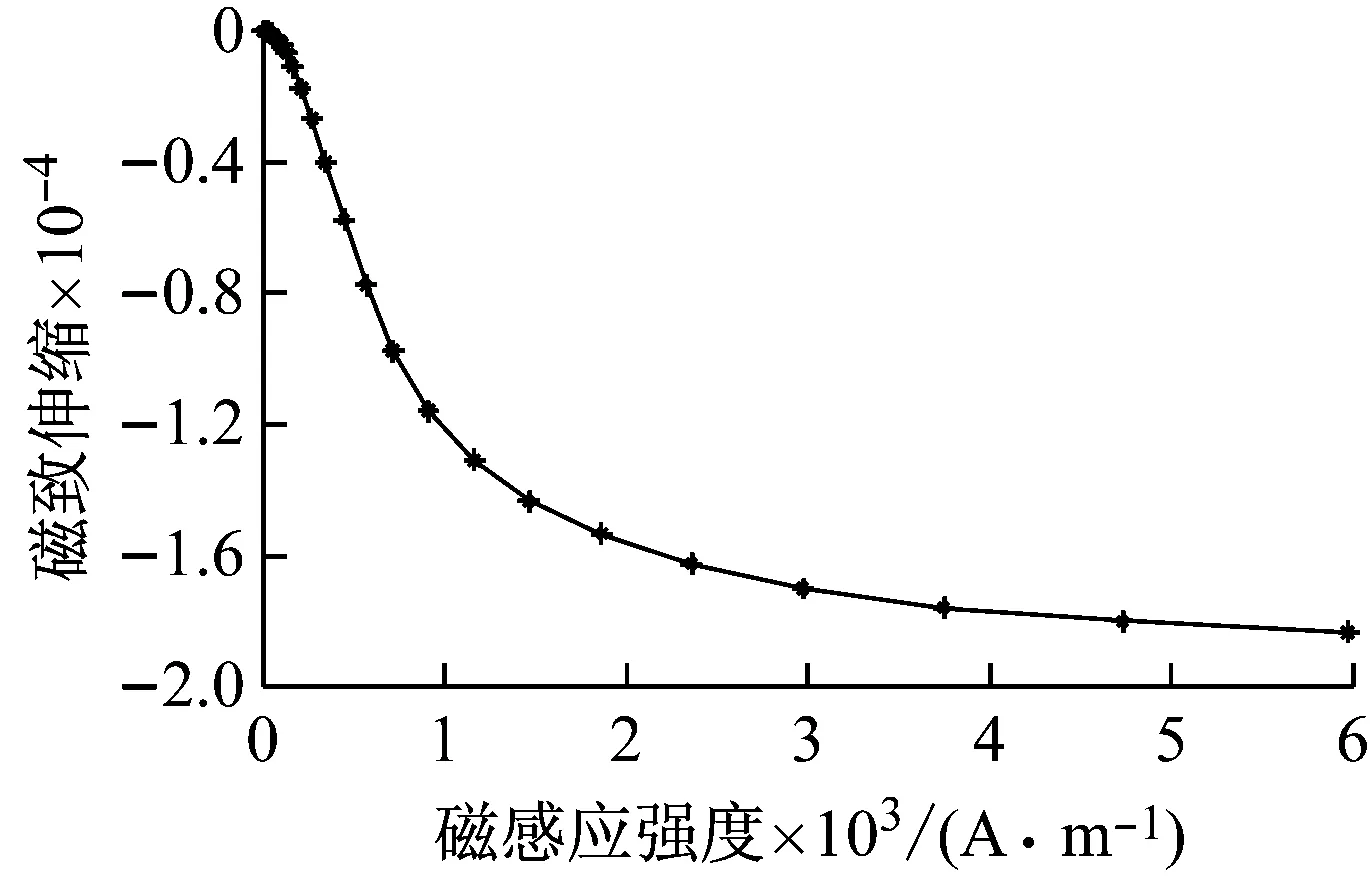
(b) 磁致伸缩与磁场的关系

2 电抗器电磁-机械耦合模型

本文所研究的电抗器振动主要来源于铁心材料的磁致伸缩以及铁心饼之间的电磁力，因此电抗器的电磁-机械系统的总能量包括磁场能、应变能、电流位能、磁边界位能、磁致伸缩能。系统的能量泛函可表示为

(1)

(2)

式中：E为杨氏模量；α为泊松比；υ为磁阻率，满足H=υB；J为外电流密度。从式(2)可以看出，能量泛函数是关于磁矢量A和位移矢量u的多元函数，根据泛函求取极值的条件

(3)

由此形成整体有限元离散方程

SX=F

(4)

式中:S为系数矩阵，包含了磁场和机械场的刚度矩阵；X为未知量列向量，即节点矢量磁位A和振动位移u的未知参数；F为已知的列向量。通过求解式(4)可得到节点矢量磁位A和振动位移u，实现电抗器磁场与机械场的耦合计算。

3 仿真结果与分析

3.1 模型建立

选用一台干式铁芯串联电抗器作为研究对象，电抗器结构如图5所示。

图5 单相铁心电抗器模型Fig.5 The structure of single phase reactor

从图5可以看出，电抗器的振动主要原因在于气隙处的电磁吸力和铁心硅钢片的磁致伸缩力以及气隙漏磁引起的旁路效应。为了更好的了解电磁力和磁致伸缩效应对电抗器振动的影响，对电抗器铁心施加不同的载荷即单独施加麦克斯韦力、磁致伸缩及两者共同作用，仿真结果如图6所示。

由图6可知，电磁力使铁心沿竖直方向有被压缩的趋势，这是因为铁心饼之间存在的麦克斯韦力总是相互吸引的力，其引起铁心的最大位移是1.7×10-6m，而铁心在磁化过程中，沿磁力方向硅钢片的尺寸要增加，而垂直于磁力线方向的硅钢片尺寸要缩小，磁致伸缩效应使铁心有被拉伸的趋势，引起铁芯振动位移最大值为9.52×10-6m，两者共同作用下铁心的最大位移是8.26×10-6m。可见电磁力与磁致伸缩效应对电抗器铁心振动有相互抵消的作用。

3.2 基于NGMM的振动分析

本文将负超磁致伸缩材料填充在铁心气隙内，材料的几何尺寸为厚度：5 mm，截面积：112 cm2。在工程应用中，为了获得更大的磁致伸缩系数，可根据电抗器中磁场的分布，在制作负超磁致伸缩材料时，使磁致伸缩性能强的方向与电抗器中负超磁致伸缩材料所处位置的磁场强方向一致。根据材料测试可知，磁致伸缩为磁场的函数，并以将测试结果应用于数值计算，得到的位移分布如图7所示。

从图6(c)和图7可以明显看出，改进后的电抗器(即用负超磁致伸缩材料Sm-Nd-Fe作为填充物)最大振幅明显低于传统型电抗器，改进型电抗器的最大振幅为7.16×10-6m,而传统型电抗器的振幅为8.26×10-6m，振幅降低了13%以上。为了更好的观察减振的效果，在测试点的选择上选取铁轭正中心点A、拐角B点和铁心柱点C，如图4所示。图8给出了传统材料下以及采用负超磁致伸缩材料填充铁心饼气隙后电抗器正常工作时的振动位移对比图。

(a)麦克斯韦力铁心位移云图

(b)磁致伸缩力铁心位移云图

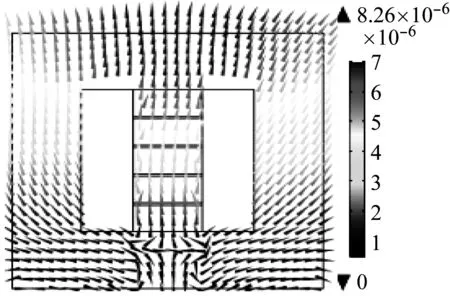
(c)两者共同作用铁心位移云图

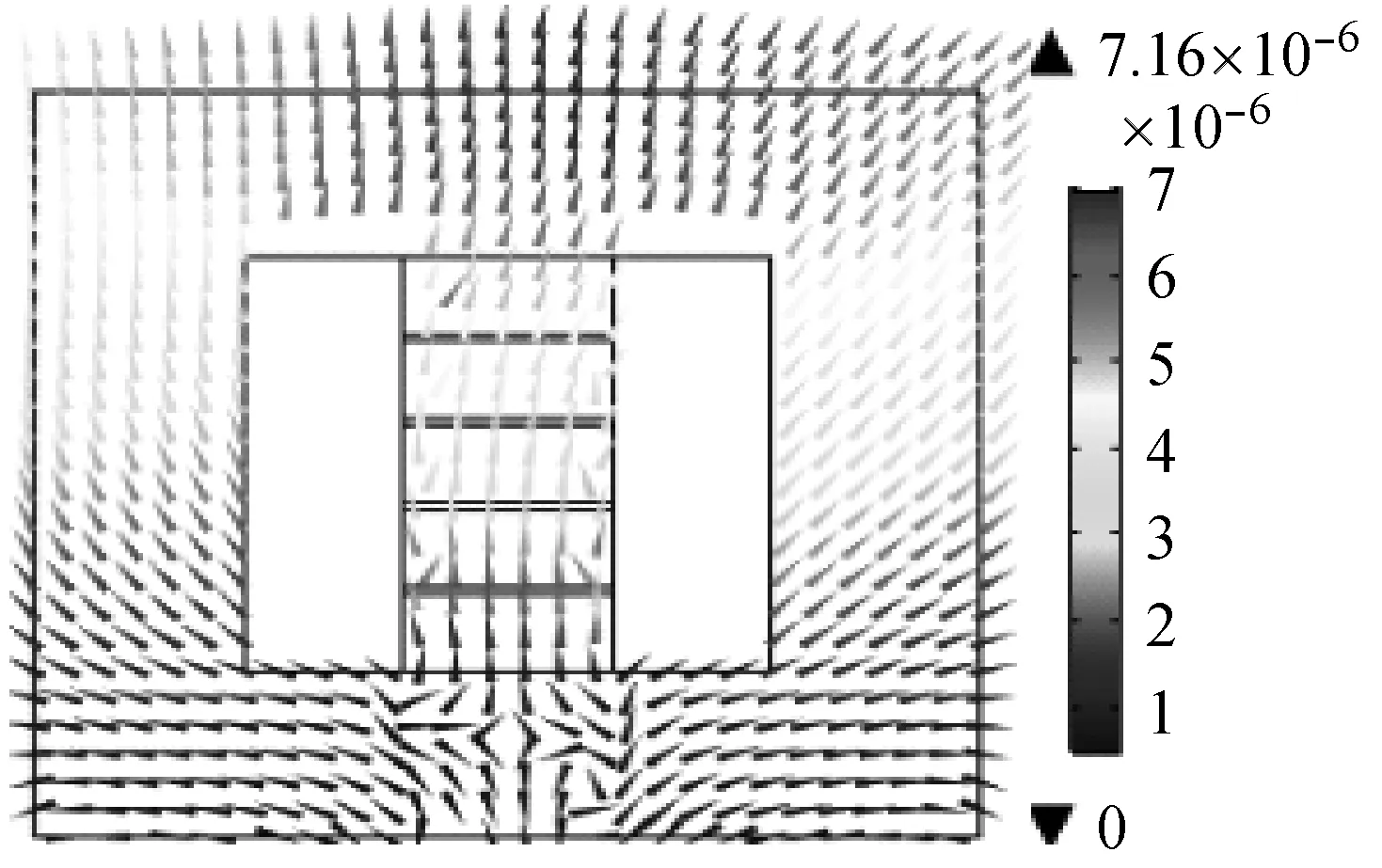
图7 NGMM填充的电抗器位移分布Fig.7 Displacement distribution of reactor filled with NGMM

由图8可知，改进后的电抗器振动幅度明显降低。为了更加直观地分析电抗器的振动信号，对A点的时域信号进行快速傅里叶变换得到频域曲线，如图9所示。

从电抗器振动信号的频谱可以看出，改进前后电抗器的频谱曲线变化趋势几乎一致，具有相同的振动特征频率，振动信号主要是100 Hz频率分量，且100 Hz倍频成分所占的比重很小。而改进后的电抗器振动幅值明显下降，对铁心自身造成的振动达到了一定程度的抑制。通过筛选合适的负超磁致伸缩材料和结构的优化设计可进一步提高电抗器的减振效果。

(a)观察点A

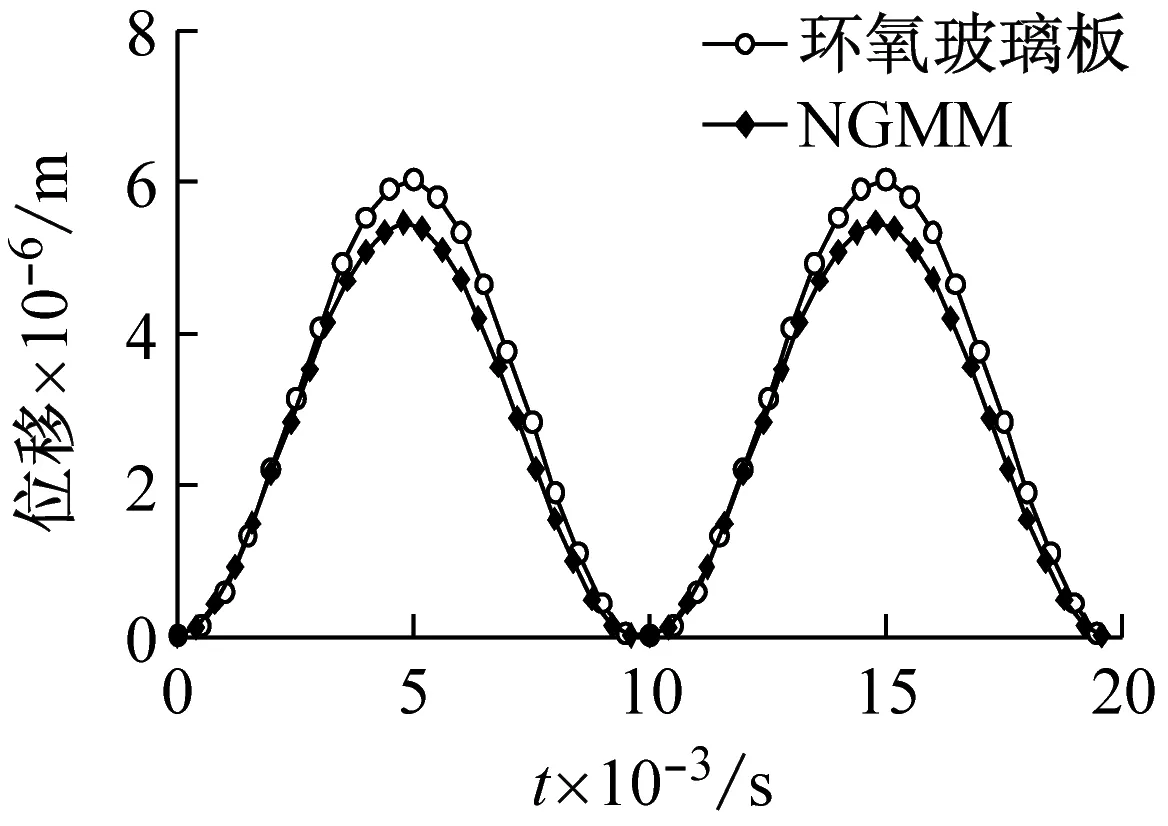
(b)观察点B

(c)观察点C

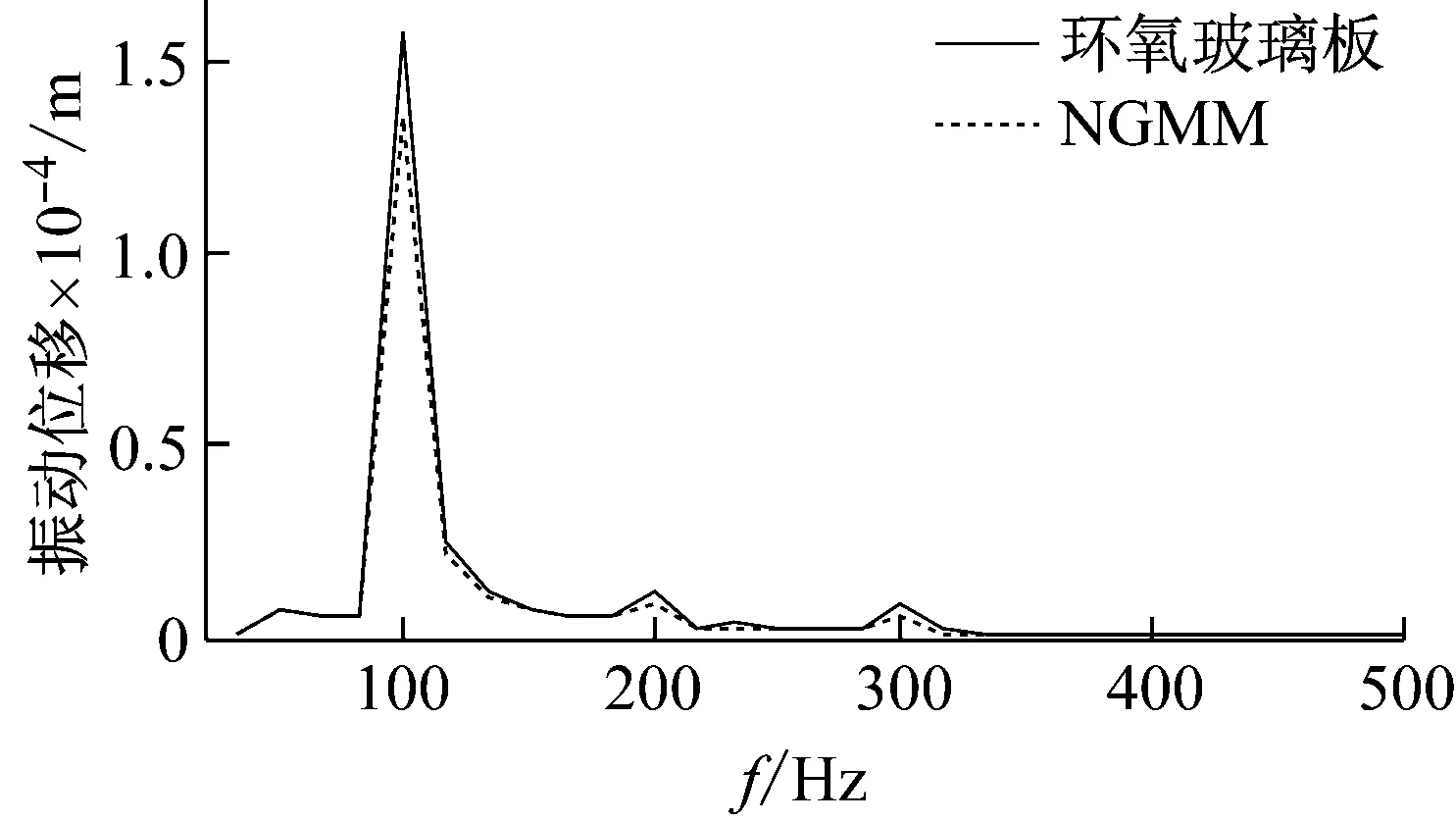
图9 不同材料填充的电抗器振动频谱图Fig.9 Frequency spectrum vibration of reactor filled with different materials

4 结 论

本文建立考虑磁致伸缩效应与电磁力共同作用下电抗器的电磁-机械耦合数值模型，通过对电抗器铁心饼之间填充不同的材料即填充环氧玻璃板或者NGMM材料，对比分析减振措施实施前后电抗器铁心的振动位移。研究结果表明，负超磁致伸缩材料填充后电抗器的振动位移减小了13%。本文提出的基于负超磁致伸缩材料的减振方法可用于一般电工设备的低噪声设计阶段。