随机地震作用下剪力墙结构振动台试验研究
2018-10-19徐亚洲刘克东刘章军苏宁粉
徐亚洲,刘克东,刘章军,苏宁粉
(1.西安建筑科技大学 土木工程学院,西安 710055;2.三峡大学 土木与建筑学院,湖北 宜昌 443002)
地震作用具有显著的随机性[1]。早在1947年Housner即将结构地震反应视为一种随机振动,许多研究者针对随机地震动开展了深入细致的研究[2]。迄今为止,结构随机地震响应分析仅限于数值分析。柳伟等[3]基于概率密度演化理论研究了环形隔板对圆柱形罐体中液面晃动响应的影响。刘章军等[4]应用非平稳地震动概率模型,对重力坝随机地震反应和抗震可靠度进行了分析。但几乎没有土木建筑结构随机试验研究的报道。
剪力墙结构作为目前民用住宅中使用最为广泛的一种结构形式,其抗震性能一直是研究者关注的重点。王维等[5]开展了预制剪力墙结构和预制剪力墙隔震结构的1/4缩尺模型振动台试验,比较了两者的结构动力特性和地震反应,并研究了装配式剪力墙水平接缝连接的可靠性。李书进等[6]对武汉世贸锦绣长江地段的某超高层住宅进行了1/30的缩尺模型振动台试验,研究了结构在6度多遇、6度设防、6度罕遇、7度罕遇地震作用下的动力反应。
但现有的剪力墙振动台试验研究均只按照规范要求选波开展确定性地震反应试验研究,没有考虑地震作用的随机性。然而,众所周知,地震动无论在时间、空间、强度和频谱上都具有很强的随机性。一条地震波仅可视为随机过程的一次样本实现,即使相同地点、同一结构也不可能遭受完全相同的两次地震作用。
为了在振动台试验过程中考虑地震动的随机性,本文在随机过程正交展开理论[7-8]的基础上,实现了采用基本随机变量的函数形式来构造随机地震动过程[9-10]。基于非平稳地震动概率模型和规范反应谱,利用基本随机变量的离散代表点集,生成了适用于7度设防的34条非平稳多遇地震动样本。同时,设计和制作了一个1/5缩尺的12层钢筋混凝土剪力墙模型进行振动台试验研究[11],开展了结构随机地震响应测试,基于试验结果分析了主要响应量的均标、准差、变异系数,并估计了相应的概率密度函数。
1 模型设计及制作
1.1 模型简介
原型结构为7度设防、Ⅱ类场地,设计地震分组为第一组,该类剪力墙结构的抗震等级为二级。根据试验条件和目的,确定模型的几何相似系数Sl为1/5,其他相似系数可由量纲分析法确定。综合考虑原型结构的特点、振动台设备条件以及模型材料制备等方面的因素,试验最终采用的主要相似系数见表1。基于此,设计了一个相对规则的12层现浇剪力墙结构模型(仅包含一个标准层),模型平面布置如图1所示。其中模型结构总高度为7.2 m,每层层高为0.6 m,平面尺寸为1.8 m×1.8 m。

图1 试验模型建筑平面图Fig.1 Plane layout of the model
模型制作完成后高度为7.55 m(包括底座),总质量13.36 t,其中模型结构与基础底座的质量为11.8 t,附加质量为1.56 t。制作完成后的模型见图2。

表1 模型主要相似关系Tab.1 Similarity constants of the model

图2 剪力墙模型全貌Fig.2 Schematic of the shear wall model
1.2 模型材料
采用细石微粒混凝土来模拟原型结构中的C40混凝土,并用镀锌铁丝来模拟钢筋。经试配后最终确定微粒混凝土的配合比为,水泥∶石子∶沙子∶水∶石灰=1∶3.64∶3.64∶1.11∶0.5。实测所得微粒混凝土的弹性模量为E=7 030 MPa,立方体抗压强度均值为fcu=8.94 MPa,质量密度为2 500 kg/m3。
2 试验方案
2.1 测试方案
试验主要测试模型的动力特性及34条随机地震动作用下结构的加速度反应和位移反应。根据测试目标,分别在模型X向及Y向中轴线位置上沿地梁顶到12层顶每层布置加速度计和位移计来分别记录模型结构的加速度和位移。
2.2 随机地震动生成
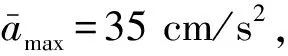
(1)


[cos(ωkt)Xk+sin(ωkt)Yk]
(2)
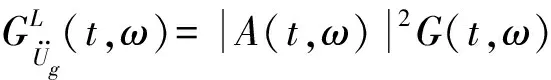
谱表示-随机函数方法中,Xk与Yk为标准正交随机变量,即:
E[Xk]=E[Yk]=0;E[XjYk]=0;
E[XjXk]=E[YjYk]=δjk
(3)
式中:E[·]表示数学期望;δjk为Kronecker记号。
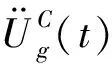
(4)

本文将基本随机变量均匀离散为34个代表点集,由谱表示-随机函数方法生成34条随机地震动样本。图3为上述方法生成的一条代表性样本时程,可以发现该样本具有非平稳地震动加速度过程的典型特征。图4为34条代表性样本时程均值反应谱与目标反应谱(规范反应谱)的比较。可以发现,均值反应谱与目标反应谱吻合良好,平均误差为6.23%。长周期部分(大于4.5 s)误差稍大,但本模型结构的主要自振周期不在该范围内。
2.3 加载方案
根据相似性原理,对地震波进行时间轴上的压缩,则原始波经压缩后的总时长为8.94 s,加速度幅值相似比为1。此外,为了测试模型结构的初始动力特性、了解不同阶段结构的损伤发展状况,在试验之前以及每隔9条随机波加载后对模型结构进行白噪声扫频,记录和分析模型结构自振频率、振型、和阻尼比等动力参数的变化,避免结构损伤累积过大,保证每条地震动样本作用下结构的响应具有可比性。考虑白噪声扫频,随机地震动试验加载工况共计39个。

图3 代表性地震动样本时程Fig.3 Representative time history of ground motions

图4 集合平均反应谱与规范反应谱的比较Fig.4 Comparison between the averaged response spectrum of 34 samples and the code’s response spectrum
3 试验结果
3.1 结构动力特性
每隔9条随机地震动试验后,均用白噪声对模型结构进行扫频。通过对加速度测点频谱特性、传递函数的分析,获得了模型结构在随机地震动加载前后的自振频率、阻尼比和振型比较。由图5可以发现五次扫频所得前两阶振型基本重合,此即说明:施加34条随机地震动前后结构的自振频率未发生明显变化,结构整体处于弹性状态。此外,随机地震动加载前后白噪声扫频测得的模型结构刚度和阻尼比也基本一致,如表2所示。
3.2 模型加速度反应
试验模型在每条样本地震波下的动力反应是本次试验测试的主要目标之一,分析各层在样本地震动作用下的加速度时程记录,可以得到模型的随机动力响应。图6为典型随机地震动作用下模型结构X方向顶部加速度时程和相对位移时程样本。
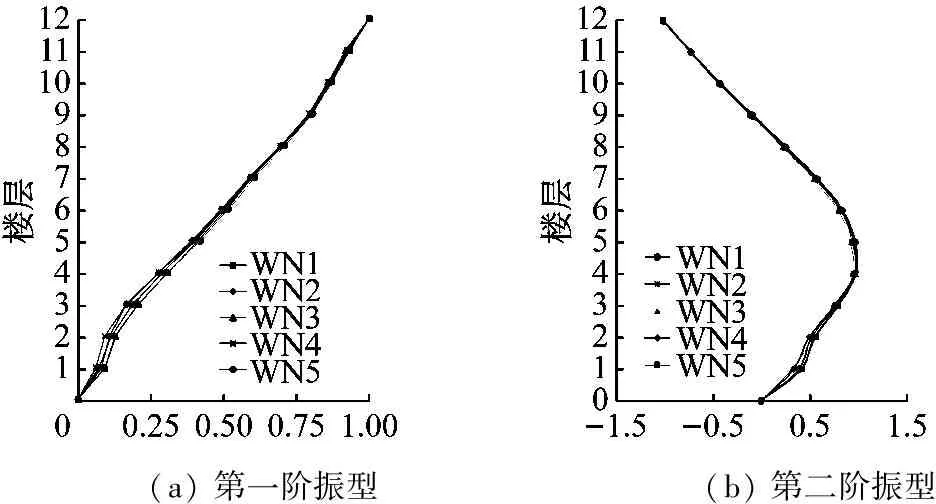
(a) 第一阶振型(b) 第二阶振型

表2 结构自振频率、阻尼比Tab.2 Natural frequency and damping ratio

(a) 12层加速度时程
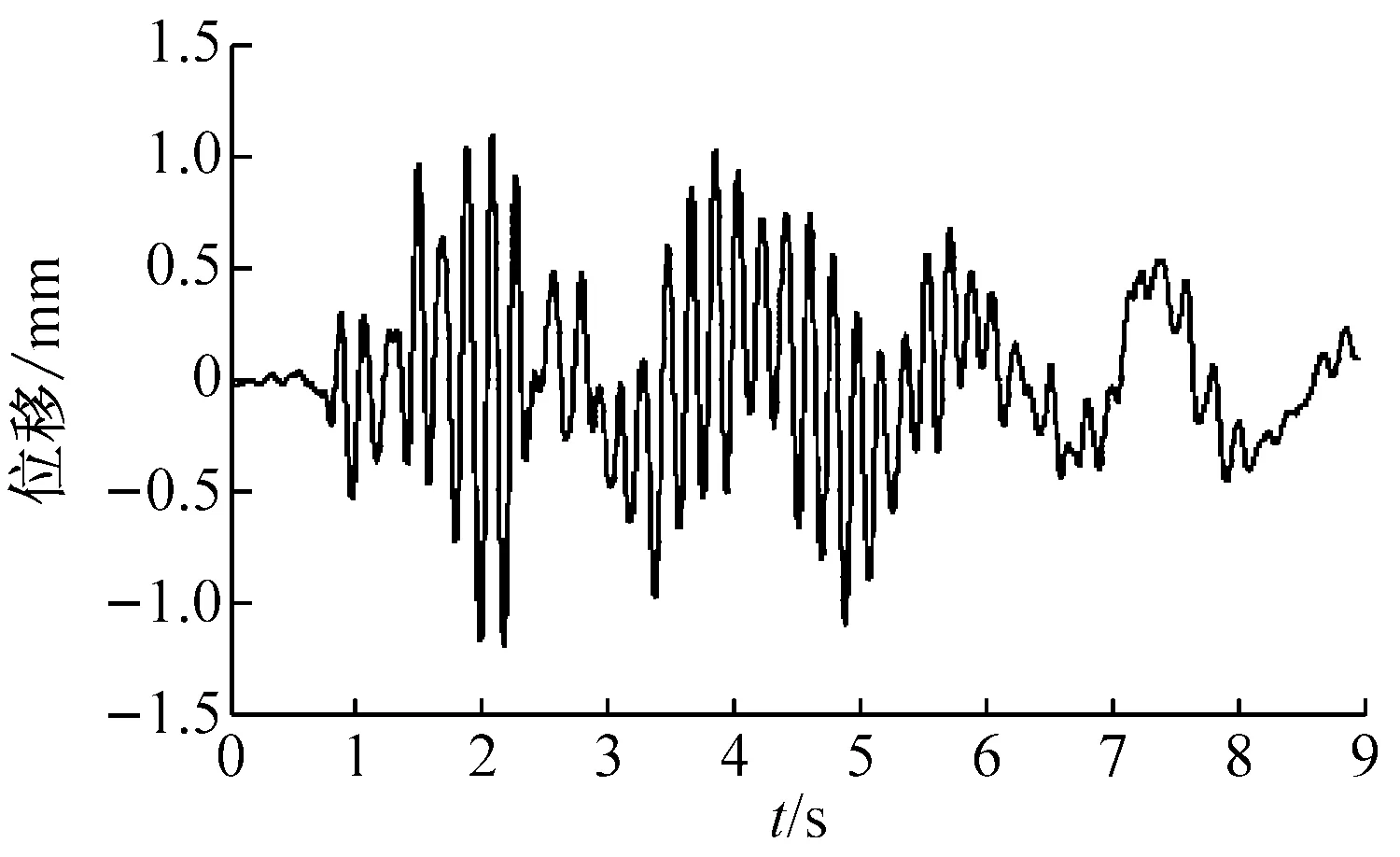
(b) 12层位移时程
以布置在地梁顶面加速度计实测的加速度最大值作为参考,将模型结构各层加速度响应在同一工况下的峰值与其相比,得到模型各层加速度反应的放大系数。图7为模型结构在34条样本地震动作用下加速度放大系数沿楼层分的布图,加速度放大系数均值随着楼层的增高而增大,模型以第一振型为主,呈弯曲变形,变异系数和标准差随着楼层的增高而增大,表明其离散性亦随楼层增高而增大。通过MATLAB中的Ksdensity函数可以估计出响应量的概率密度函数。图8为34条随机波作用下每层的加速度放大系数概率密度曲线,可以看出其离散性,表现出明显的随机涨落现象。随着楼层的增高概率密度函数趋于扁平,与图7中变异系数和标准差的变化趋势吻合。

图7 加速度放大系数均值和标准差Fig.7 Mean and standard deviation of acceleration magnification factors
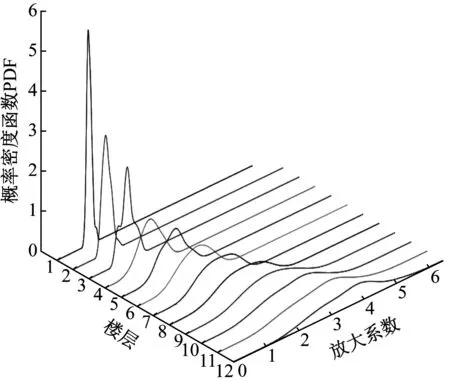
图8 加速度放大系数概率密度曲线Fig.8 Probability density functions of acceleration magnification factors
图9给出了34条样本地震动作用下层间剪力沿楼层的分布图。与加速度放大系数相反,楼层剪力是由各个楼层的惯性力累积叠加并传递到底部形成基底剪力,导致离散性随着楼层的降低而增大,基底剪力均值为6.14 kN。图10给出了楼层剪力的概率密度函数,从图中可以看出随着楼层的降低楼层剪力概率密度函数亦呈现出扁平分布趋势,与图9的样本曲线分布吻合。
3.3 模型位移反应
层间侧移角是抗震规范中控制结构延性的一个重要设计指标,图11给出了实测的34条随机地震动作用下模型结构各层的最大层间侧移角。可以发现,层间侧移角的较大值发生在第2层和第5层及第11层处,其标准差也在相应楼层处出现峰值,说明这些楼层为该结构的薄弱层。层间侧移角均值的最大值出现在第5层,为1/1 767,与试验过程中第5层连梁处较早出现裂缝相吻合(如图12所示)。图13为各个楼层层间位移角的概率密度函数,其均值大多集中在1/4 000到1/2 500,而薄弱层第2、5、11层的概率密度曲线均值偏大,且呈现扁平状,表现出较大的离散。
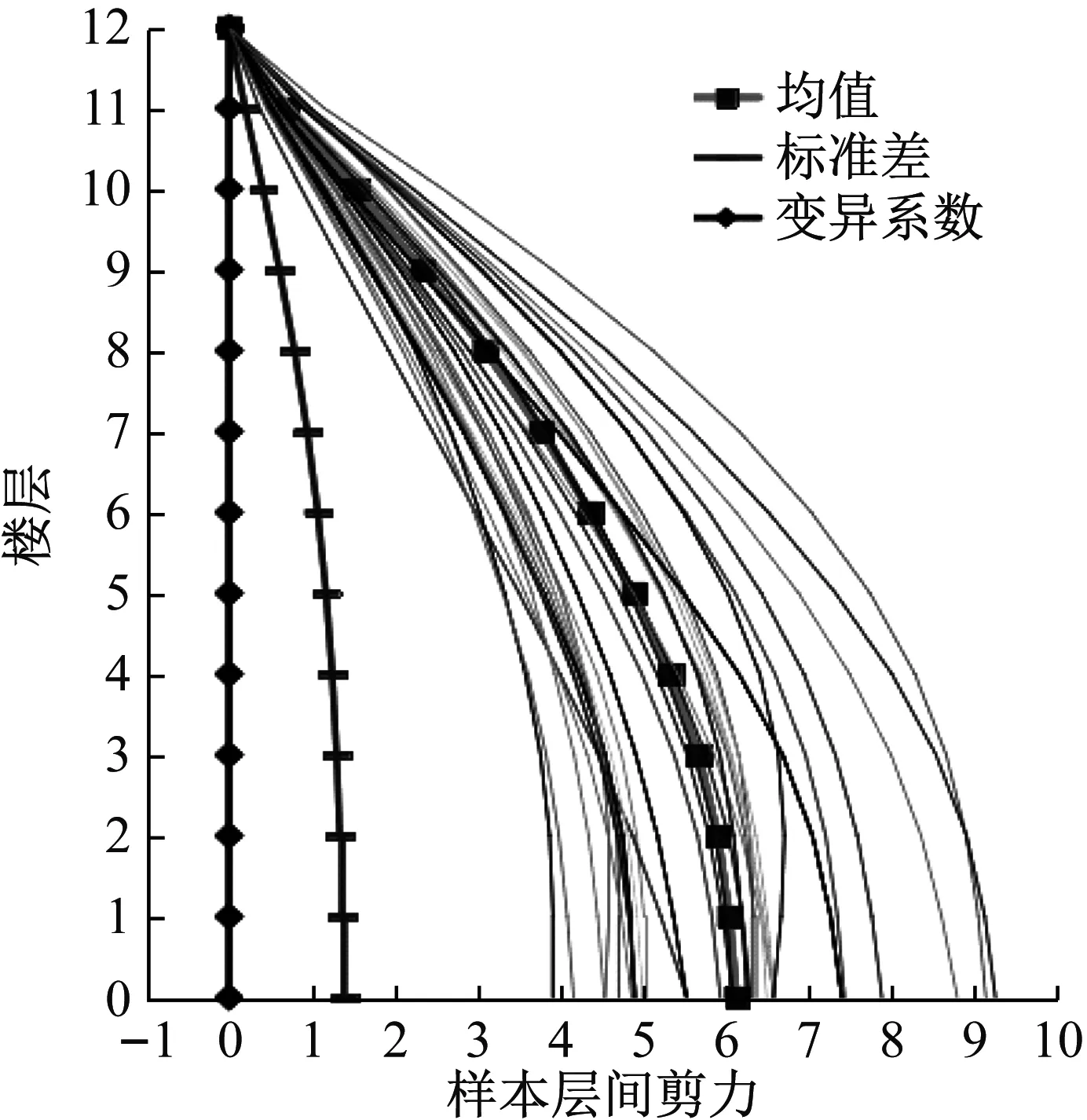
图9 楼层剪力均值及标准差Fig.9 Mean and standard deviation of floor shear forces

图10 楼层剪力概率密度曲线Fig.10 Probability density functions of floor shear forces

图11 层间侧移角均值和标准差Fig.11 Mean and standard deviation of drift angles

图12 五层连梁裂缝Fig.12 Crack of a coupling beam at the fifth floor

图13 层间侧移角概率密度曲线Fig.13 Probability density functions of drift angles
为了更详细地分析结构的随机地震反应,分别计算了模型结构随机地震反应的均值、标准差及概率密度函数。限于篇幅,本文仅给出最大层间侧移角所在第5层侧移角的均值、标准差时程及典型时刻的概率密度函数。图14(a)和(b)为模型结构第5层层间侧移角均值和标准差时程,可以发现均值最大的时刻发生在3秒左右,且不超过1/4 000。图14(c)为典型时刻的第5层层间侧移角概率密度函数,可以看出在多遇地震作用下不同时刻地震反应的概率密度函数有所不同,表明结构位移反应具有一定的随机性。
图15(a)和(b)是基底剪力的均值和标准差时程,基底剪力的均值发生在2 s时刻约为1 kN,标准差最大时刻也出现在2 s附近。图15(c)是典型时刻基底剪力的概率密度函数,表现出一定的随机涨落现象,且与标准的正态分布有差异。
4 结 论
本文设计和制作了1/5缩尺的十二层钢筋混凝土剪力墙结构模型,基于谱表现-随机函数方法生成了34条全非平稳地震动加速度样本,将其作为随机输入开展了振动台试验研究。通过动力特性测试获得了模型结构的振型、频率、阻尼比等。进而,基于结构地震响应样本分析了加速度放大系数、最大层间侧移角、基底剪力等关键地震响应的均值和标准差,并估计了典型时刻各个响应量的概率密度函数,讨论了离散性沿楼层传播的变化规律。振动台响应试验结果表明,模型结构基底剪力的反应表现出明显的随机涨落,且结构反应的概率分布呈非正态分布特征。试验和分析所得剪力墙结构随机地震响应可为结构随机地震反应模拟及可靠度分析提供参考。
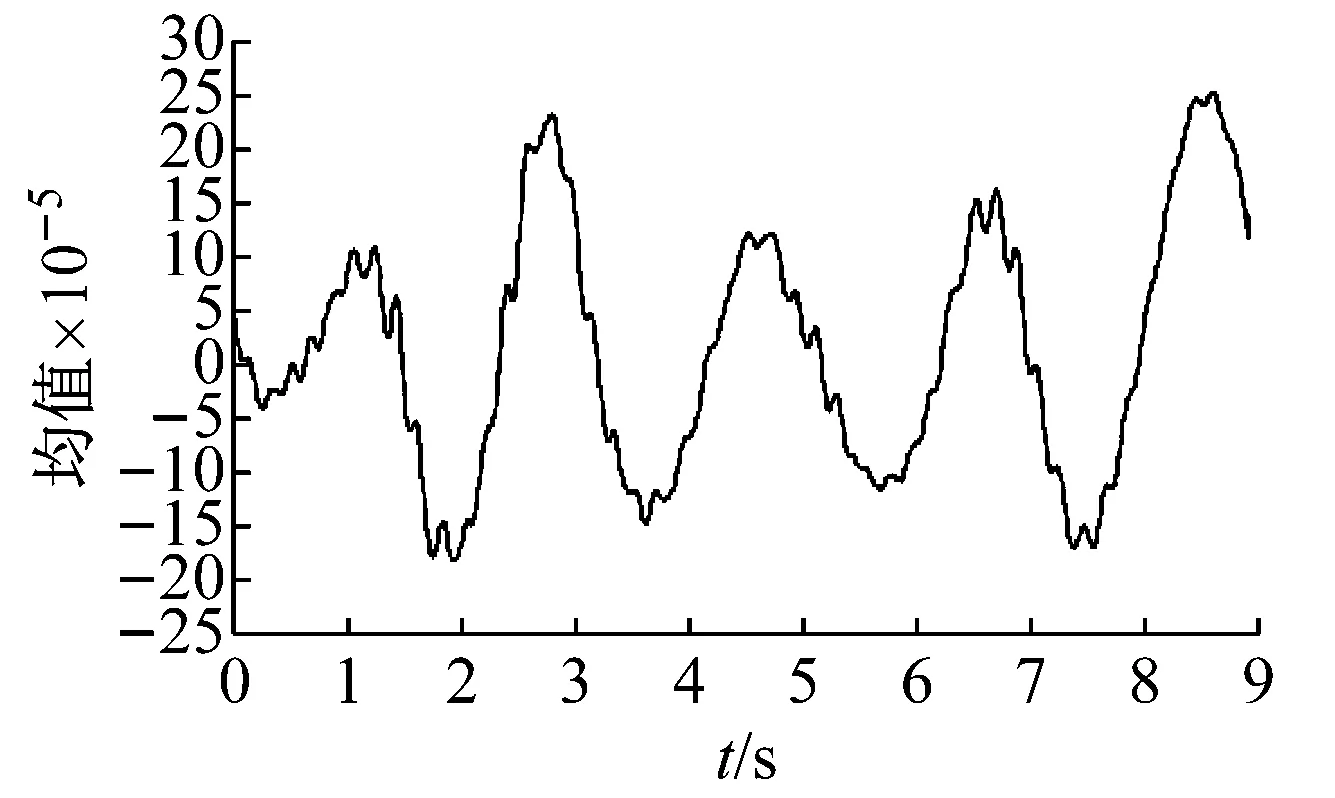
(a) 第5层层间侧移角的均值时程

(b) 第5层层间侧移角的标准差时程

(c) 典型时刻第5层层间侧移角概率密度函数

(a) 基底剪力均值时程

(b) 基底剪力标准差时程
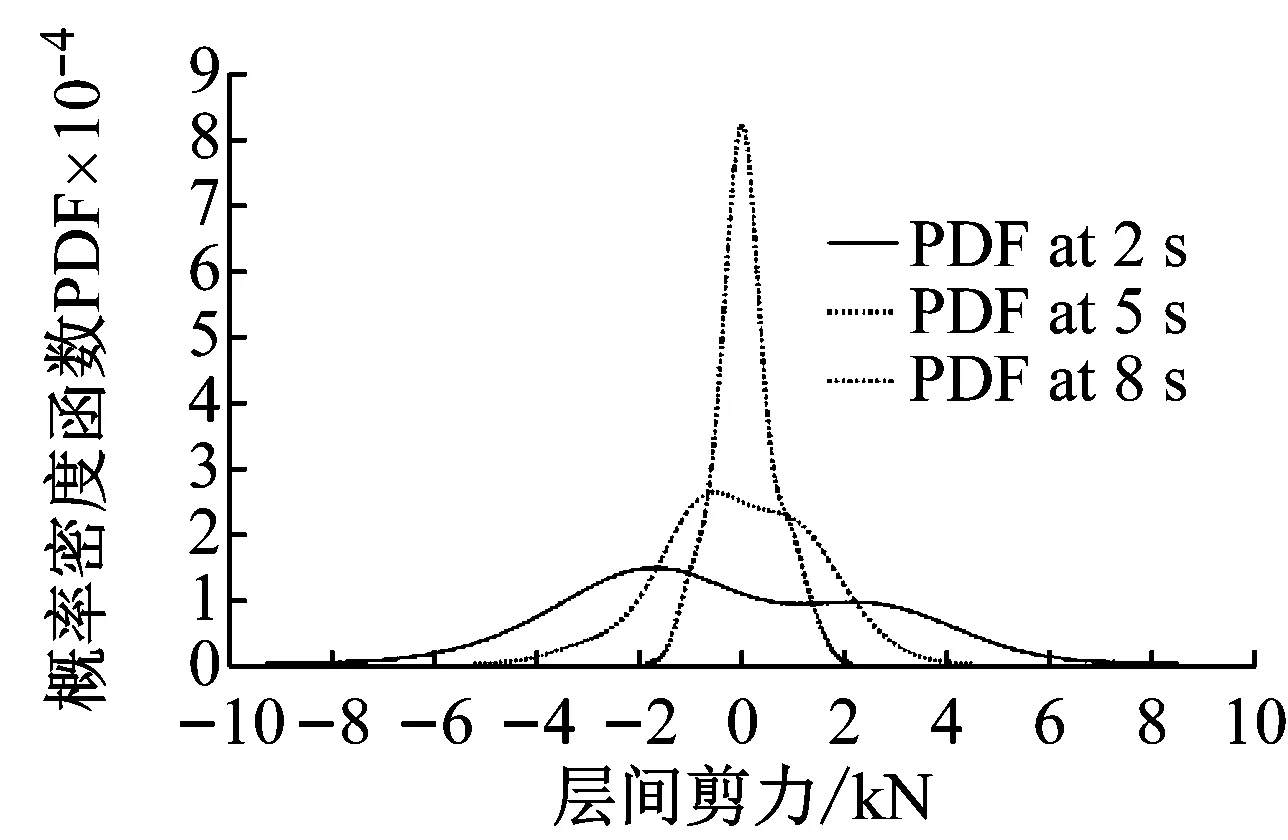
(c) 典型时刻基底剪力概率密度函数
