一种基于地震早期辐射P波能量的高速铁路Ⅰ级地震警报预测方法

宋晋东，教聪聪，李山有，侯宝瑞，汪 源

(中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080)

地震预警指的是在地震发生后，利用震源附近地震台站观测到的地震波初期信息，快速估计地震参数并预测地震对周边地区的影响，抢在破坏性地震波到达震中周边地区之前，发布各地地震动强度和到达时间的预警信息，向目标区域提供数秒至数十秒的预警时间，使企业和公众能够提早采取地震紧急处置措施，进而减轻地震人员伤亡和财产损失，是近年来发展起来的减轻地震灾害的有效手段之一[1-3]。地震预警的关键技术包括震级快速估算、定位、烈度预测等[4]。世界上现有多个国家和地区已建立或正在测试地震预警系统，如日本[5-6]、墨西哥[7]、美国[8-9]、意大利[10-11]、中国[12-13]、中国台湾[14-15]等，也取得了一定的减灾效益[16-17]。对于高速铁路，地震是一种发生概率较小、但对行车安全有极大危害的自然灾害，高速铁路发达国家如日本、法国等均建立了地震紧急处置系统[18]，中国是地震多发国家、且高速铁路发展迅速，迫切需要建设高速铁路地震紧急处置系统。

高速铁路地震紧急处置均应实现三级地震警报，由低到高分为Ⅰ级、Ⅱ级和Ⅲ级，不同的处置等级分别对应相应的紧急处置措施，相应的实测或预测加速度值分别为40 cm/s2、80 cm/s2、120 cm/s2 [19]。一般来说，当实测加速度峰值(此处为低通5Hz滤波后水平向加速度记录的合成值[20]，下文中用PGA表示)达到40 cm/s2时，破坏性地震波已经到来[21]，留给高速铁路紧急处置的时间较短，若能利用地震P波预测地震最终是否将会达到预先设定的地震警报PGA阈值，即可以提高紧急处置的时效性。

高速铁路地震紧急处置的工作方式主要采用区域和现地两种。区域方式在快速估计出震源参数后，主要利用地震动衰减关系判断地震对铁路沿线可能造成的破坏，但地震动衰减关系的不确定性[22]、目标区域的场地条件[23]、大震级事件时的破裂尺度[24]等诸多因素都会造成预测结果的误差，同时，高速铁路的地震监测台站布设较为稀疏，也不利于区域方式这样的工作模式。现地方式主要利用地震动参数的P波段与全波段统计关系[25-26]，但仅仅通过幅值类参数进行预测，难以区分小震近震与大震远震，因此，适用于高速铁路紧急处置的现地地震动预测方法值得进一步研究。

本文以准确、快速预测高速铁路Ⅰ级地震警报为目标，利用日本K-net强震数据，基于能够表征地震破裂辐射能量的地震动参数速度平方积分IV2与加速度峰值PGA的线性统计关系，通过P波触发后1 s、2 s、3 s时间窗IV2对应的Ⅰ级地震警报阈值预测地震动是否能够达到40 cm/s2。同时，引入能够稳定估计震级M的参数特征周期τc，以P波触发后1 s、2 s、3 s时间窗τc的阈值表征大震级事件，以此体现预测模型中震级对预测结果的影响，旨在探索一种具有理论地震学依据的高速铁路Ⅰ级地震警报预测方式。

1 数 据

从日本K-net强震观测台网中，选择了2007年10月至2015年10月发生于陆地的地震事件作为研究对象，对强震数据做如下处理与筛选：

(1) 选取震源深度10 km以内、震中距100 km以内的强震数据，对于5级以上地震，补充100～200 km范围的强震记录；

(2) 对强震数据进行P波到时自动识别[27]，并做人工P波到时捡拾校正；

(3) 对加速度记录积分一次得到速度记录、速度记录积分一次得到位移记录，积分后的记录作0.075 Hz巴特沃斯高通滤波以消除积分带来的低频漂移现象；

(4) 计算τc需要地震记录满足一定的信噪比要求，选取P波触发后3秒内的速度幅值大于0.05 cm/s作为信噪比的选取标准筛选数据[28]。

经过上述数据处理流程后，共筛选出1 258次地震、共5 439组(16 317条)强震数据供本文进行研究。图1显示了本文所选取地震的震中及记录台站分布图，震级与震中距的统计关系如图2。由图2可见，本文选取强震数据的震级范围3.0～8.0、震中距范围0～200 km。

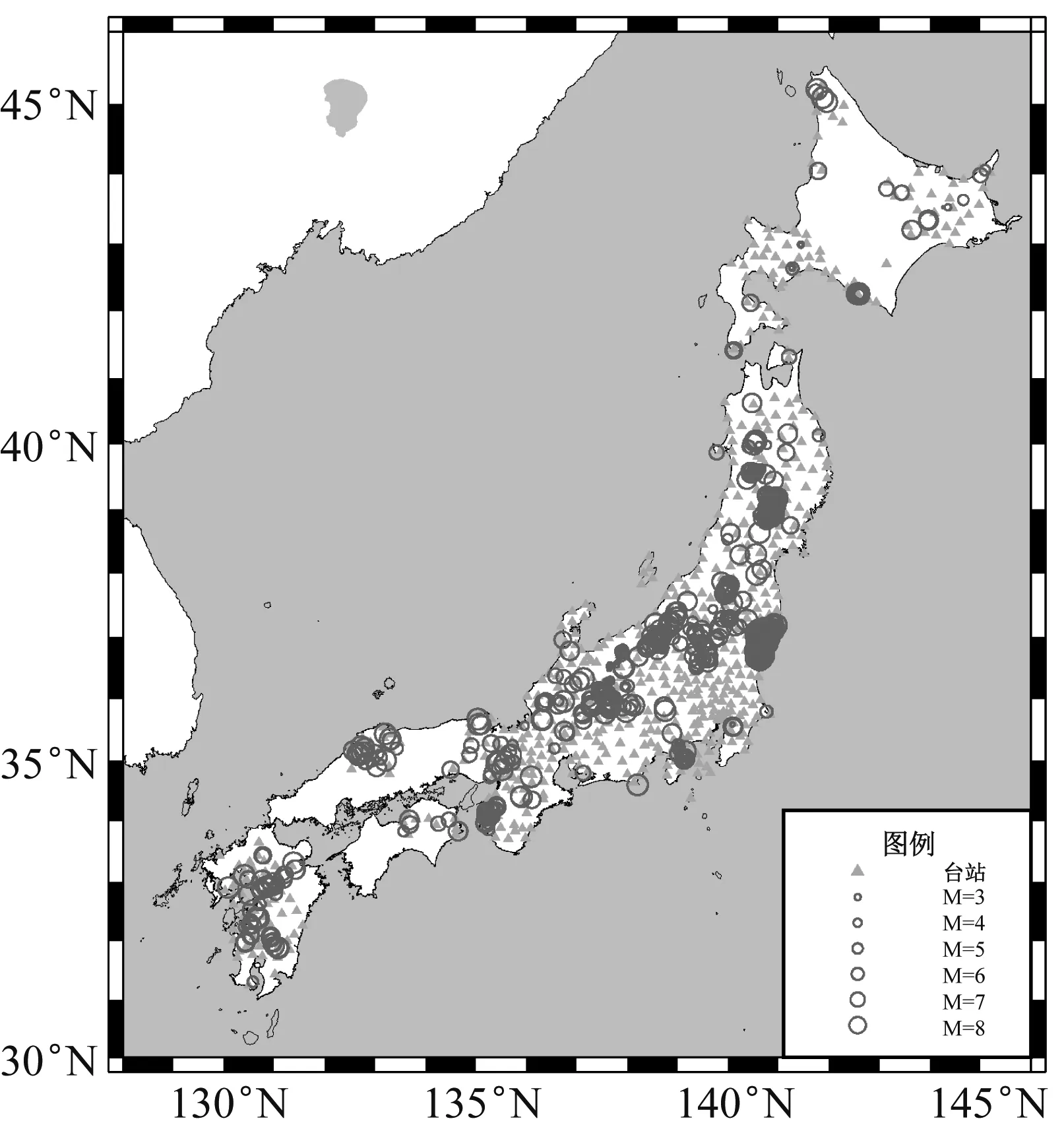
图1 本研究中的地震震中(空心圆，直径与震级大小成比例)及K-net台站分布图(灰色三角形)
Fig.1 Locations of the epicenters (red open circles,size in proportion to magnitude) and K-net stations (grey solid triangles) in this study

2 方 法

2.1 四水准预测方法模型

本文方法的主要思想是预测接收到地震波的台站能否达到Ⅰ级地震警报对应的PGA阈值，在利用IV2预测PGA的基础上，引入τc参数表征震级M的影响，依据P波段τc阈值和IV2阈值分为4个预测水准，分别为0，1，2，3，图3显示了本文提出的四水准预测方法模型，各个预测水准的定义如下

图2 强震数据的震中距及震级分布图Fig.2 Distribution of the number of strong ground motion records as a function of the magnitude and epicentral distance

0：小震级事件，PGA预测值小于40 cm/s2，在台站周边不会发生地震破坏；

1：大震级事件，PGA预测值小于40 cm/s2，在远离台站处可能发生地震破坏，即大震远震；

2：小震级事件，PGA预测值大于40 cm/s2，在台站周边可能产生破坏，即小震近震；

3：大震级事件，PGA预测值大于40 cm/s2，在台站周边和远离台站处都会产生破坏，即大震近震。

由于地震震级越大所造成的地震破坏也可能随之增大，本文从预测准确性的角度考虑，选取预测水准3即P波段τc和IV2同时大于预先确定的阈值时，预测会达到Ⅰ级地震警报、即PGA会达到40 cm/s2。因此，首先需要利用本文筛选并处理的强震数据建立两个统计关系，即τc与震级M的线性统计关系、PGA与IV2的线性统计关系，并以这两个统计关系作为预测方程，确定震级M=6对应的τc阈值、以及PGA=40 cm/s2对应的IV2阈值。

图3 本文提出的四水准预测Ⅰ级地震警报方法模型Fig.3 Four alert levels for predicting first-level earthquake alarm of high-speed railway proposed by this paper

2.2 速度平方积分IV2与PGA的线性统计关系及其阈值确定

速度平方积分IV2是一个与地震早期辐射能量紧密相关[29]的震级估计参数[30]，同时，Brondi等[31]的研究结果显示出IV2与峰值速度、豪斯纳烈度存在很高的相关性，王子珺等也验证了IV2与峰值加速度、峰值速度、谱烈度的高相关性，因此速度平方积分IV2可以快速评判地震破坏，IV2的计算公式如下

(1)

式中:v为速度记录，t0为积分的起始点，一般为P波的触发点，Δt为积分计算的时间窗长。

在本研究中将PGA作为预测的地震动参数对象，利用本文收集处理的K-net强震数据，分别建立P波触发后1 s、2 s、3 s时间窗下IV2与PGA的线性统计关系。如图4所示，灰色圆点表示每条强震记录的IV2值，实线表示拟合后得到的PGA与IV2线性统计关系，虚线分别表示线性统计关系的±1σ标准差。从安全冗余的角度考虑，借鉴Zollo等的方法，选取+1σ标准差PGA与IV2线性统计关系，转换得到PGA=40 cm/s2时对应的P波触发后1 s、2 s、3 s时间窗下IV2阈值，详见表1和图4。

表1P波触发后1s、2s、3s时间窗下PGA=40cm/s2对应的IV2阈值
Tab.1ThresholdsofIV2referencetoPGA=40cm/s2fortimewindowsof1s,2sand3safterP-wavearrival

P波触发后的时间窗/sIV2/(cm2·s-1)10.0120.0230.04

图5显示了选取+1σ标准差PGA与IV2线性统计关系时lg PGA估计值与lg PGA真实值误差的概率密度函数，其整体服从正态分布，概率密度函数的形状也随着时间窗的增长呈现陡度增加的趋势，P波触发后1 s、2 s、3 s时间窗下lg PGAest-lg PGA的标准差分别为0.35，0.31，0.29，这与线性关系标准差吻合、且有随时间窗增长而减小的趋势，这些都表明了PGA与IV2有着很强的线性统计关系，由于选定了+1σ标准差的线性统计关系，因此+1σ标准差的线性统计关系所对应的概率为85%，如图5阴影部分所示，依据Zollo等的研究结果，+1σ标准差即85%的概率可以满足方法的可靠性要求。

2.3 特征周期τc与震级M的线性统计关系及其阈值确定

地震触发后P波初期的频率成分是地震预警中常用的一种估算震级M参数，一般通过建立其与震级M的线性统计关系进行震级的快速估算。该方法由Nakamura(1988)提出并应用于日本新干线UrEDAS地震紧急处置系统，Allen等(2003)将此方法运用于美国南加州的地震预警系统测试，Kanamori[32]在Nakamura方法的基础上提出了τc参数估算震级，τc的计算公式如下

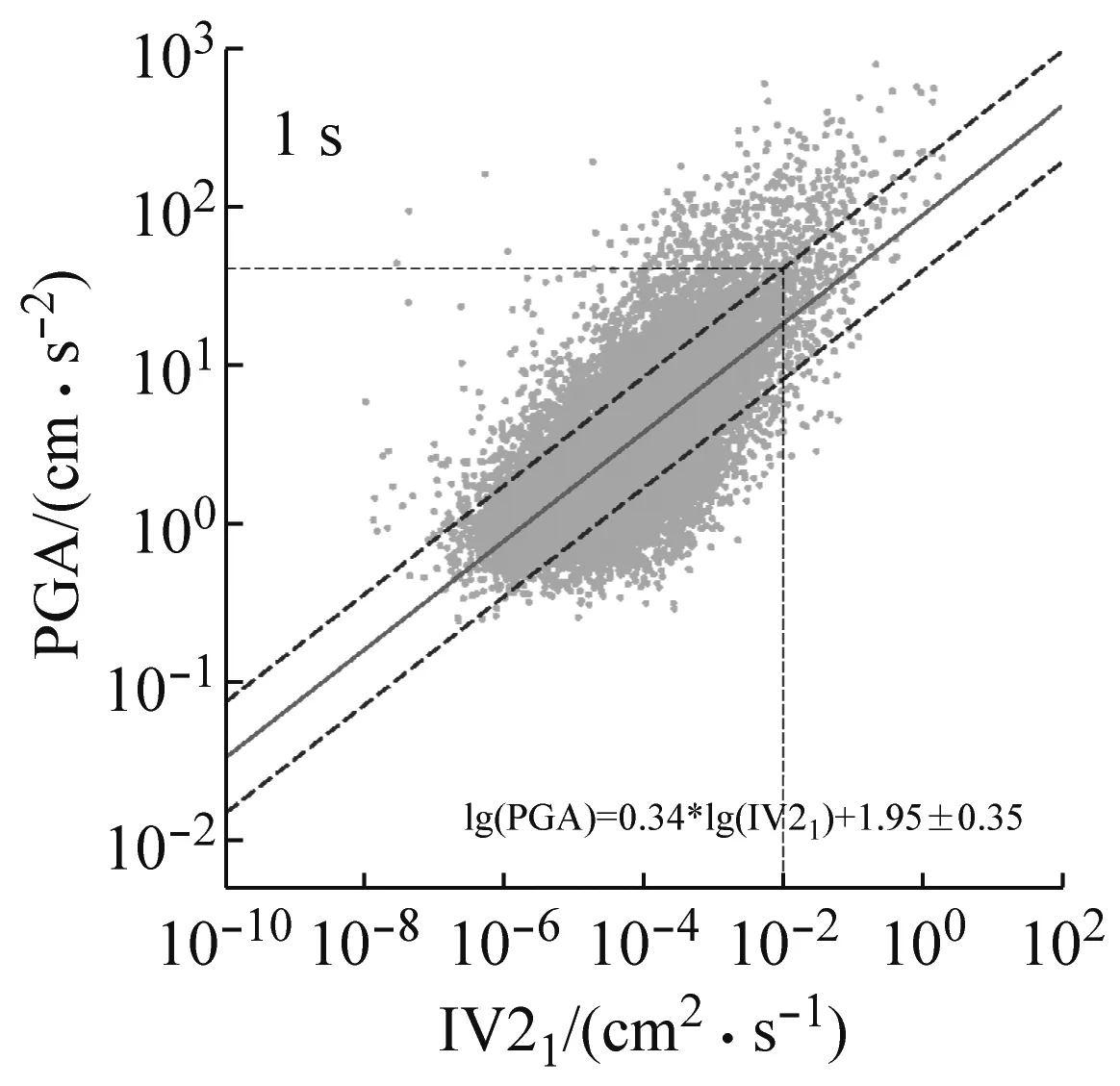
圆点表示每条强震记录的IV2计算结果；实线表示拟合后得到的PGA与IV2的线性统计关系；虚线分别表示线性统计关系的±1σ标准差；图中还标出了+1σ标准差PGA=40 cm/s2时对应的IV2阈值

图4 P波触发后1 s、2 s、3 s时间窗下PGA与IV2的线性统计关系
Fig.4 Empirical scaling relationships between PGA and IV2 from time windows of 1s,2s and 3s after P-wave arrival

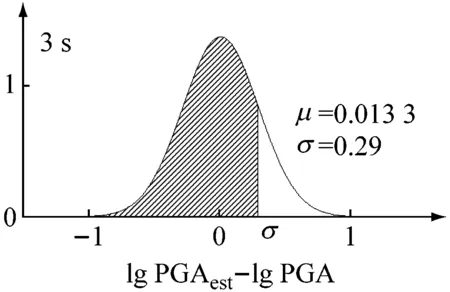
图5 P波触发后1 s、2 s、3 s时间窗+1σ标准差PGA与IV2线性统计关系时lg PGA估计值与lg PGA真实值误差的概率密度函数Fig.5 The probability density function (pdf) of lg PGAest-lg PGA allowing for the 1+σ error bounds of empirical scaling relationships between PGA and IV2 from time windows of 1 s,2 s and 3 s after P-wave arrival

(2)

其中，

(3)

0为P波到时点，τ0为积分计算的时间窗长，一般取3 s，v(t)表示竖向速度时程，u(t)表示竖向位移时程。由计算公式可以得出，τc表征的是地震波的特征周期，同时也是0-τ0积分步长内的平均周期。本文分别选择P波触发后1 s、2 s、3 s时间窗分别计算τc值。

利用本文收集处理的K-net强震数据，分别建立1 s、2 s、3 s时间窗下τc与震级M的线性统计关系，如图6所示，圆点表示每条强震记录的τc值，实线表示拟合后得到的τc与震级M的线性统计关系，虚线分别表示线性统计关系的±1σ标准差。

Zollo等(2010)的研究结果表明，τc随震中距的变化并不显著，即τc是只与M相关的参数、与震中距不相关，因此，可以将τc作为可以稳定表征震级M大小的参数。本文依据Zollo等的研究结果将震级M=6时定义为大震级事件，从安全冗余的角度考虑，借鉴Zollo等的方法，选取-1σ标准差τc与震级M的线性统计关系，转换得到震级M=6时对应的P波触发后1 s、2 s、3 s时间窗下τc阈值，详见表2和图6。

表2P波触发后1s、2s、3s时间窗下震级M=6对应的τc阈值
Tab.2ThresholdsofτcreferencetoM=6fortimewindowsof1s,2sand3safterP-wavearrival

P波触发后的时间窗/sτc/s10.6020.6530.72

图7显示了选取-1σ标准差τc与M线性统计关系时M估计值与M真实值误差的概率密度函数，其整体同样服从正态分布，但概率密度函数的形状并未出现随着时间窗的增长而陡度明显增加的趋势，表明P波触发后1 s即可获得稳定的震级估计结果，这与宋晋东等[33]的研究结果一致。P波触发后1 s、2 s、3 s时间窗下Mest-M的标准差分别为0.89、0.82、0.79，这与线性关系标准差吻合、且有随时间窗增长而减小的趋势，这些都表明了τc与M有着很强的线性统计关系，由于选定了-1σ标准差的线性统计关系，因此-1σ标准差的线性统计关系所对应的概率为85%，如图7阴影部分所示，依据Zollo等的研究结果，-1σ标准差即85%的概率可以满足方法的可靠性要求。

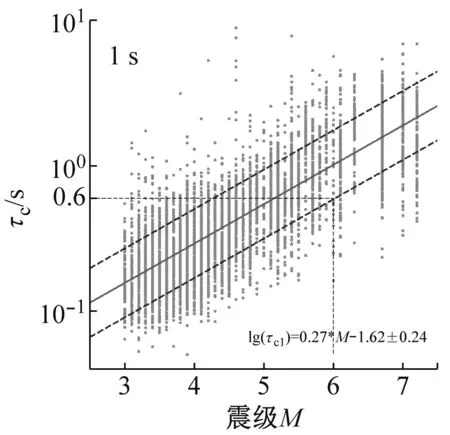
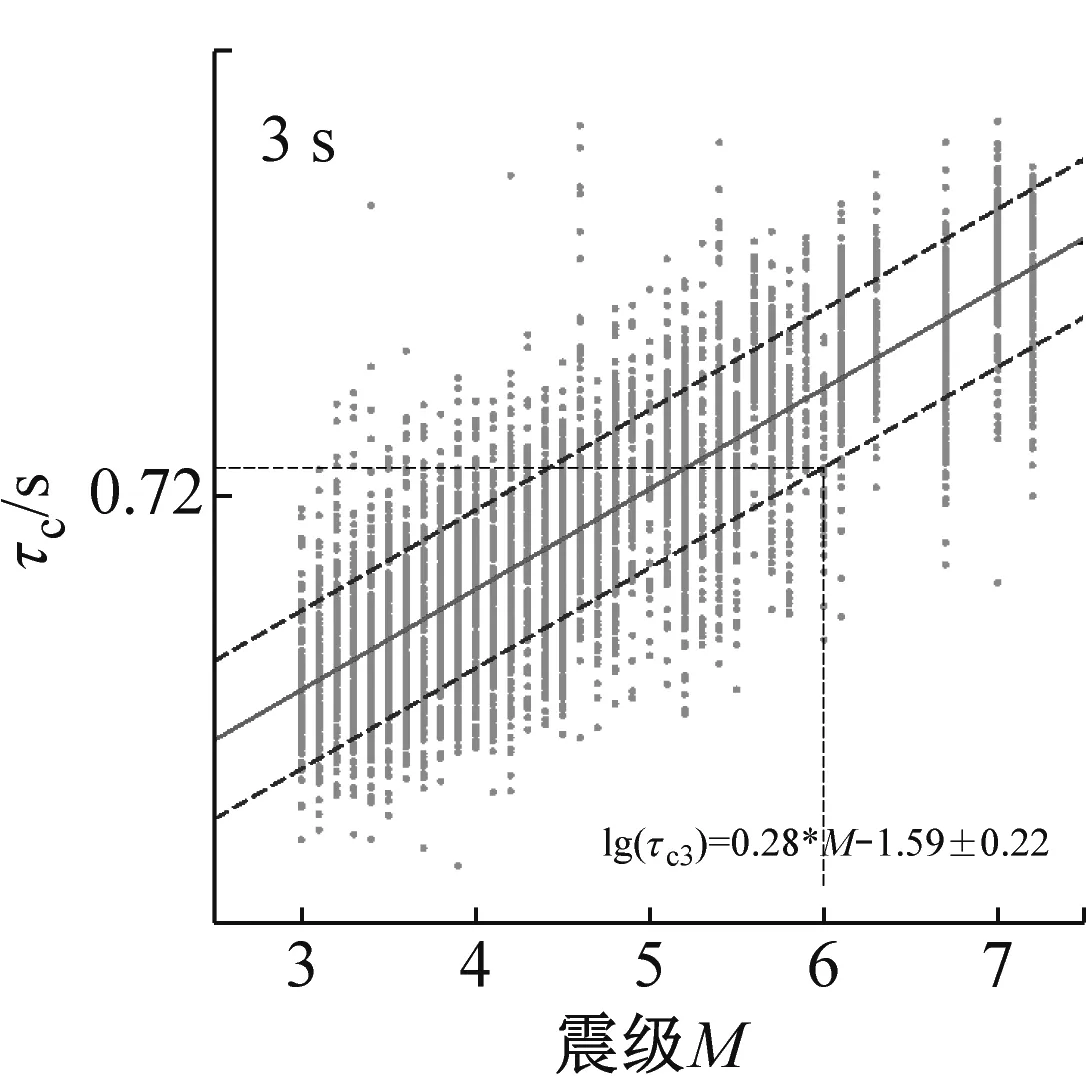
圆点表示每条强震记录；实线表示拟合后得到的τc与震级M的线性统计关系；虚线分别表示线性统计关系的±1σ标准差；图中还标出了-1σ标准差震级M=6时对应的τc阈值

图6 P波触发后1 s、2 s、3 s时间窗下τc与震级M的线性统计关系
Fig.6 Empirical scaling relationships betweenτcand magnitude from time windows of 1 s,2 s and 3 s after P-wave arrival

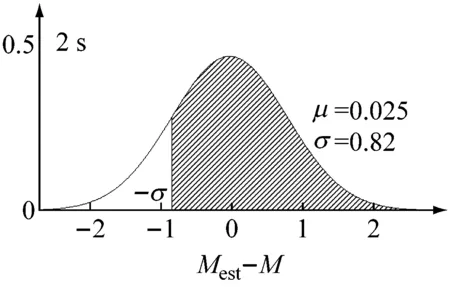
图7 P波触发后1 s、2 s、3 s时间窗-1σ标准差τc与M线性统计关系时M估计值与M真实值误差的概率密度函数Fig.7 The probability density function (PDF) of Mest-M allowing for the -1σ error bounds of empirical scaling relationships between τc and magnitude from time windows of 1 s,2 s and 3 s after P-wave arrival

3 2016年4月14日熊本6.5级地震震例分析

2016年4月14日21时26分(日本标准时间)，日本熊本县熊本地方发生6.5级(Mj)地震，震源深度11 km。九州新干线一列6节车厢编组的新干线800系电力动车组(时速80 km/h)从熊本站开往熊本综合车辆所的回厂过程中发生脱轨，脱轨地点距离熊本站南侧1.3 km，距离震中约14 km。

日本防灾科学技术研究所(NIED)布设的K-net强震观测台网中，共有10个台站位于九州新干线沿线，图8显示了此次熊本地震的震中位置(五角星)、九州新干线列车脱轨位置(叉形)、以及九州新干线沿线K-net台站位置(菱形)以及记录到的PGA最大值(台站编号后的括号内)。其中，编号KMM006的K-net台站记录到了最大PGA值521.1 cm/s2，该台站在这10个台站中距离震中位置最近，震中距为6.4 km。共有5个台站的实测PGA值超过了40 cm/s2，按照PGA值由小到大顺序排列，台站编号分别为FKO011(62.7 cm/s2)、KMM003(76.3 cm/s2)、KMM012(156.8 cm/s2)、KMM008(290.7 cm/s2)、KMM006(521.1 cm/s2)，即这5个K-net台站都至少达到了Ⅰ级地震警报的水准。列车脱轨的位置位于KMM008台站与KMM006台站之间，这两个台站记录到的PGA值在九州新干线沿线10个K-net台站中，分别为最大和第二大。表3列出了九州新干线沿线10个K-net台站P波触发后1 s、2 s、3 s的τc与IV2的计算结果。

在2016年4月14日熊本6.5级地震震例分析中，主要验证本文方法的准确性与时效性。在准确性分析中，主要利用九州新干线沿线10个K-net台站数据，预测各个台站是否会达到Ⅰ级地震警报。在时效性分析中，基于KMM006与KMM008台站数据，分析在这两个台站在P波触发后多长时间窗内可以预测出达到40 cm/s2的Ⅰ级地震警报，并比较预测达到Ⅰ级地震警报的时刻、列车脱轨时刻、气象厅紧急地震速报发出时刻的先后顺序。

3.1 准确性

在准确性分析中，主要基于九州新干线沿线10个K-net台站，计算每个台站P波触发后1 s、2 s、3 s时间窗的τc和IV2值，基于本文分析得到的τc阈值和IV2阈值，依据本文提出的预测水准方法模型，预测各个台站是否会达到40 cm/s2的Ⅰ级地震警报，并与台站的实测PGA进行比较，分析预测结果的准确性。图9中，实心方框表示台站的实测PGA<40 cm/s2，空心方框表示台站的实测PGA>40 cm/s2，台站边的数字表示该台站的预测水准。

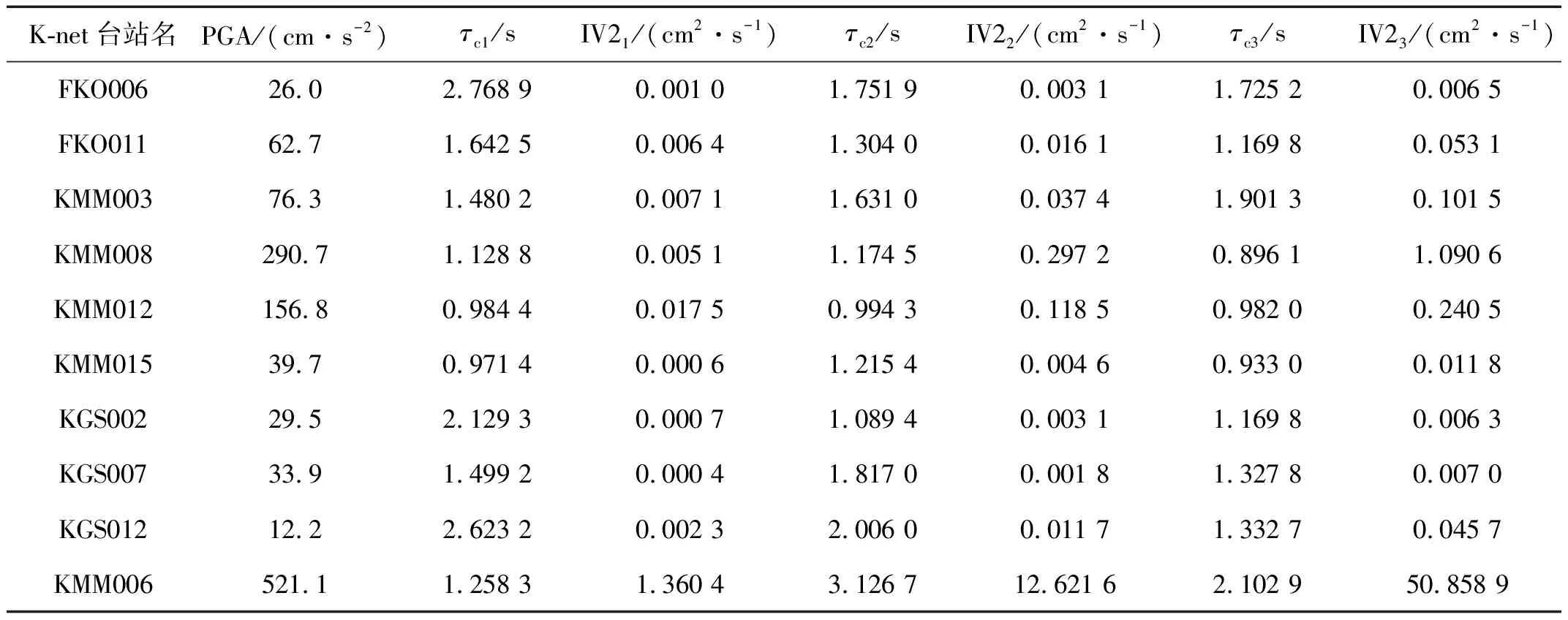
表3 P波触发后1 s、2 s、3 s时间窗下τc与IV2的计算值Tab.3 Calculating values of τc and IV2 for K-net stations along Kyushu Shinkansen from time

当每个台站P波触发1 s时，距离震中最近的KMM006台站达到预测水准3，即表明可以预测出Ⅰ级地震警报。10个沿线K-net台站中，预测准确的台站数为6个，FKO011台站、KMM003台站、KMM008台站为漏报，KGS012台站为误报。

当每个台站P波触发2 s时，距离震中最近的KMM006台站达到预测水准3，即表明可以预测出Ⅰ级地震警报。10个沿线K-net台站中，预测准确的台站数为8个，FKO011台站为漏报，KGS012台站为误报。

当每个台站P波触发3 s时，距离震中最近的KMM006台站达到预测水准3，即表明可以预测出Ⅰ级地震警报。10个沿线K-net台站中，预测准确的台站数为9个，KGS012台站为误报。

需要注意的是，水准2也可以表征PGA预测值大于40 cm/s2，但由于其代表小震级事件，而地震震级越大所造成的地震破坏也可能随之增大，故本文从预测准确性的角度考虑，选取了预测水准3作为达到Ⅰ级地震警报的标准。虽然在准确性分析中没有出现预测水准2的案例，但是对于预测水准2是否适合作为预测的标准，还值得进一步分析。

同时我们发现，在P波触发后的初期，5个实测PGA值超过40 cm/s2的台站出现了一定程度的漏报，但是随着P波触发后预测时间窗的增长，预测的结果趋向于实测。这主要是由于本文选取的速度平方积分IV2是一个与地震破裂辐射能量密切相关的地震动参数，大地震事件需要较长的时间才能够释放其累积的能量，其破裂前期释放的能量较少，因此在一个较短的时间窗内，仅能反映地震破裂的一部分能量，随着时间窗的增长，包含的能量信息也随之增加，从而使得预测结果越来越接近实测值[34]，这也符合此次地震的震源破裂过程[35]。此外，九州新干线沿线10个K-net台站中，位于最南端、距离脱轨位置最远的KGS012台站出现了误报，通过τc值与IV2值计算结果的检验，发现KGS012台站τc与IV2的计算结果都偏大，我们推测可能的原因是KGS012台站周边的场地条件导致了这种现象，虽然KGS012台站距离震中位置和脱轨位置最远，离震中最近的KMM006台站也可以迅速做出准确预测，误报在此次地震中所带来的影响会相对较小，但是在高速铁路紧急处置中保证警报的准确性尤为重要，因此，优化本文方法、降低误报与漏报几率是下一步工作需要重点考虑的问题。

五角星表示地震震中；铁轨线表示九州新干线线路；菱形表示九州新干线沿线K-net台站位置；叉形表示九州新干线列车在此次地震中的脱轨位置

图8 2016年4月14日熊本6.5级(Mj)地震九州新干线沿线K-net台站分布
Fig.8 Locations of K-net stations (diamonds) along Kyushu Shinkansen (rail line) in 2016 Kumamoto earthquake (Mj=6.5)

图9 2016年4月14日熊本6.5级(Mj)地震九州新干线Ⅰ级地震警报预测结果Fig.9 The predicting results to first-level earthquake alarm using K-net stations data along Kyushu Shinkansen in 2016 Kumamoto earthquake (Mj=6.5)

3.2 时效性

在时效性分析中，主要分析KMM006与KMM008台站在P波触发后多长时间窗内可以预测出Ⅰ级地震警报，并将这个时刻与九州新干线脱轨时刻、气象厅紧急地震速报时刻放在同一个绝对时间轴下，进行先后顺序对比。

首先分析距离震中位置最近的KMM006台站，因为该台站距离震中位置最近，且在熊本地震中获得最大PGA值。图10(a)显示了KMM006台站竖向未滤波加速度记录，记录的起始时间为2016年4月14日21时26分21秒，图10(b)以KMM06台站的PGA时程为基础，并在34 s～43 s范围内进行细部放大。由图10(b)可知，KMM006台站的P波到时点为21:26:36.66秒，依据有效性分析结果，P波触发后1 s即21:26:37.66秒可预测出Ⅰ级地震警报，台站实测达到40 cm/s2的时刻为21:26:38.8秒。依据中村丰(2016)推测，九州新干线在21:26:40.5秒时列车司机感受到了强烈震动而选择手动刹车，大约在21:26:41.0秒列车开始脱轨[36]。日本气象厅紧急地震速报系统在21:26:42.5秒时发出预警第1报，预测震级为6.5级(Mj)[37]。因此对于KMM006台站，可以在脱轨前3.34 s预测出Ⅰ级地震警报、且警报预测时刻比气象厅紧急地震速报提前4.84 s。

接着分析KMM008台站，因为该台站获得的PGA值仅次于KMM006台站，且脱轨位置位于该台站与KMM006之间。图11(a)显示了KMM008台站竖向未滤波加速度记录，记录的起始时间为2016年4月14日21时26分23秒，图11(b)以KMM008台站的PGA时程为基础，并在36 s～45 s范围内进行细部放大。图11(b)可知，KMM008台站的P波到时点为21:26:37.95秒，依据有效性分析结果，P波触发后2 s即21:26:39.95秒可预测出Ⅰ级地震警报，台站实测达到40 gal的时刻为21:26:41.28秒。因此对于KMM008台站，可以在脱轨前1.05 s预测出Ⅰ级地震警报、且警报预测时刻比气象厅紧急地震速报提前2.55 s。虽然能够提前的时间较KMM006台站相对减少，但是KMM008台站的震中距也大于脱轨位置与震中的距离，同时，KMM006台站预测Ⅰ级地震警报的时刻比KMM008台站提前近3 s，因此本文方法具有很高的时效性。

图10 2016年4月14日熊本6.5级(Mj)地震中KMM006台站Ⅰ级地震警报的预测时刻Fig.10 The prediction time for first-level earthquake alarm on K-net KMM006 station in 2016 Kumamoto earthquake (Mj=6.5)

图11 2016年4月14日熊本6.5级(Mj)地震中KMM008台站Ⅰ级地震警报的预测时刻Fig.11 The prediction time for first-level earthquake alarm on K-net KMM008 station in 2016 Kumamoto earthquake (Mj=6.5)

4 结 论

本文以准确、快速预测高速铁路Ⅰ级地震警报为目标，提出了一种基于地震早期辐射P波能量的四水准预测40 cm/s2方法。

该方法利用日本K-net强震数据，基于能够表征地震破裂辐射能量的地震动参数速度平方积分IV2与PGA的线性统计关系，通过P波段IV2对应的Ⅰ级地震警报阈值预测地震动是否能够达到40 cm/s2。同时，引入能够稳定估计震级M的参数特征周期τc，以P波段τc的阈值表征大震级事件，以此体现震级对预测结果的影响。基于IV2阈值与τc阈值，建立了四水准预测Ⅰ级地震警报的方法模型。确定预测水准3、即P波段τc和IV2同时大于预先确定的阈值时，预测会达到Ⅰ级地震警报。

以2016年4月14日熊本6.5级(Mj)地震为例，基于九州新干线沿线K-net台站强震数据，进行了地震警报的准确性与时效性分析。结果表明，本文方法可以在距离震中最近的KMM006台站P波触发后1 s预测出Ⅰ级地震警报，预测出Ⅰ级地震警报的时刻较九州新干线脱轨时刻和气象厅紧急地震速报发布时刻分别提前了3.34 s和4.84 s。对于KMM008台站，也可以在脱轨前1.05 s、气象厅紧急地震速报前2.55 s预测出Ⅰ级地震警报，虽然能够提前的时间较KMM006台站相对减少，但是KMM008台站的震中距也大于脱轨位置与震中的距离，同时，KMM006台站预测Ⅰ级地震警报的时刻比KMM008台站提前近3 s，因此本文方法具有很高的时效性。

由于速度平方积分IV2是一个与地震破裂辐射能量密切相关的地震动参数，准确性分析的研究结果也表明大地震的震源破裂过程、局部场地条件都有可能引起该方法的漏报、误报问题，因此，优化本文方法、降低误报与漏报几率是下一步工作需要重点考虑的问题。

致谢

日本防灾科学技术研究所(NIED)为本研究提供了数据支持，所有数据均从K-net网站下载(网址：http://www.kyoshin.bosai.go.jp/(最后登陆日期：2016年12月31日))，文中图件使用通用制图工具GMT(Genetic Mapping Tools)绘制。