基于统计能量分析原理的声振耦合模型全局灵敏度分析
2018-10-19蔡延年于洪亮廖建彬俞万能
蔡延年,于洪亮,,闫 锦,廖建彬,俞万能
(1.大连海事大学 轮机工程学院,辽宁 大连 116026;2.集美大学 轮机工程学院,福建 厦门 361021)
统计能量分析法(Statistical Energy Analysis,SEA)是宽频声振响应预测与分析的有力工具,广泛应用于船舶、飞机、汽车等领域。实际应用中需确定模态密度,内损耗因子,耦合损耗因子等SEA基本参数。这些参数分别反映子系统存储能量的能力,子系统的能量耗散能力以及子系统间能量的损耗情况等统计能量模型特征,共同组成统计能量分析系统矩阵。其主要确定方式为理论/数值分析方法[1]、实验测量方法[2]及理论/数值/实验相结合的方法[3]。但上述方法均是对结构参数的近似和逼近,实现在10-2~10-4数量级上的内损耗因子、耦合损耗因子的精确测量十分困难。参数的测量及估算误差逐步积累会扩大名义设计值与其真实动力学特性间的偏差,导致模型声振响应结果的不确定性,从而影响声振响应结果的精度与可靠性。不仅如此,材料试样的制造缺陷、边界条件的选择等因素同样会导致统计能量参数存在一定不确定性。
参数灵敏度分析是研究模型不同输入参数的不确定性对输出参数不确定性影响程度的方法[4]。目的在于量化输出不确定性的来源情况,为减小模型输出不确定性的最经济方式提供参考。根据单独或多个参数对模型输出的影响分为局部灵敏度分析与全局灵敏度分析。前者用于评价单一参数变化引起的模型输出的变化情况,适用于灵敏度微分方程易推导且影响因素较少的模型;后者在整个输入变量的分布空间内对输入变量对输出不确定性的影响进行分析,用于评价输入变量的相对重要程度。目前,国内灵敏度分析在统计能量模型上的应用均基于局部灵敏度分析法[5-7],仅考察单个参数变化对目标函数的影响,考虑多输入参数的实际概率分布及目标函数随整个参数空间同时变化的SEA模型全局灵敏度分析还鲜有见报。
本文将全局灵敏度分析中的傅里叶幅度灵敏度检验法(Fourier Amplitude Sensitivity Test,FAST)应用于声腔-结构-声腔三子系统声振模型,以噪声降低量和传声损失为目标函数,计算统计能量分析参数灵敏度,量化参数不确定性对声振响应结果不确定性的影响程度,建立其贡献程度的排序情况,探究不同频段下影响声振响应的关键参数。
1 声腔-结构-声腔三子系统SEA模型
在不计及侧向传声影响下,以图1所示的两个声腔被隔板(子系统2)分开的系统为研究对象。声腔分为声源室(子系统1)与接受室(子系统3),声源室内声源产生的声波通过板件子系统传递给接收室。板件为钢材,尺寸为1 m×1 m,声腔尺寸1 m×1 m×1 m,其中介质为空气,其他模型参数见表1。考虑子系统2的共振模态群与非共振模态群共同作用,物理模型可简化为图2的SEA模型。

图1 声腔-结构-声腔模型Fig.1 Cavity-structure-cavity model

图2 声腔-结构-声腔统计能量分析模型Fig.2 Cavity-structure-cavity SEA model
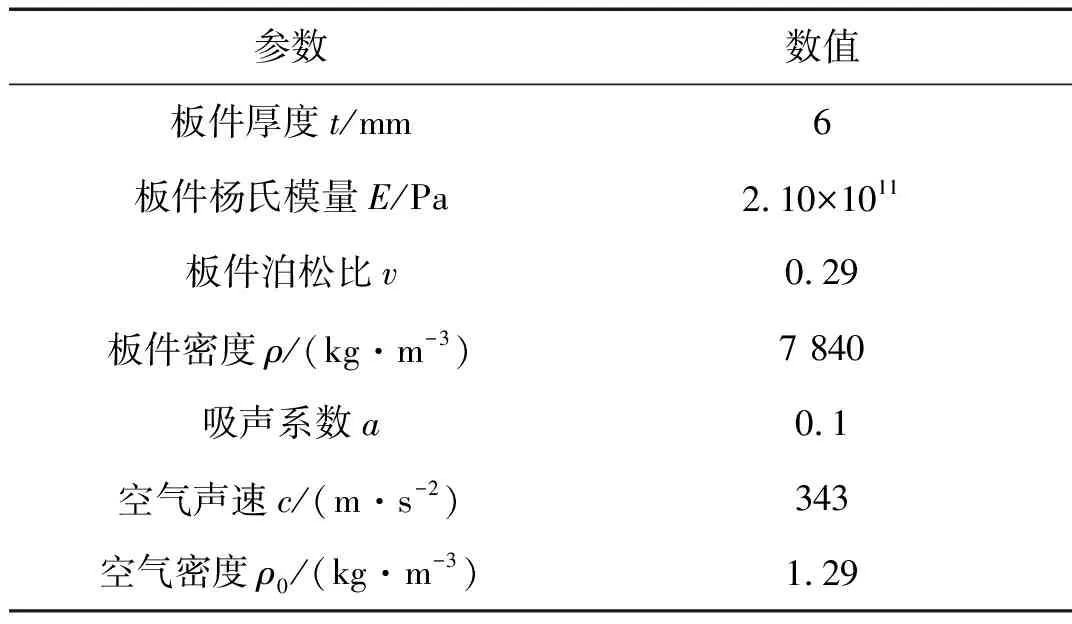
表1 声腔-结构-声腔模型基本参数Tab.1 Parameters of Cavity-structure-cavity Model
1.1 统计能量分析功率流平衡方程
统计能量分析法基于能量守恒原理,将研究对象分成若干独立的子系统,考虑各子系统的功率输入、能量损耗以及子系统间的耦合能量损耗,建立功率流平衡方程求解子系统的能量,利用其能量与状态参数关系计算各子系统的声振响应[8]。如图2所示的声腔-结构-声腔三子系统SEA模型:子系统1接受外界激励输入P1,各子系统间通过耦合连接进行能量流动,在内阻尼及耦合损耗阻尼作用下耗散能量。依据能量平衡原理建立三子系统功率流平衡方程
(1)
式中:ω=2πf,ηi为子系统内损耗因子,ni为子系统模态密度,ηij为子系统间的耦合损耗因子,Ei为子系统能量,i,j=1,2,3。
1.2 统计能量分析参数
利用统计能量分析法进行声振响应计算,关键是明确研究对象的模态密度、内损耗因子、耦合损耗等核心参数,建立准确的SEA功率流平衡方程,获取子系统的能量分布情况。
(1) 模态密度
模态密度是指某一频段内子系统单位频率的模态数,表征结构对于外界激励产生共振响应能力。声腔子系统1和3的模态密度由下式给出[9]
(2)
式中:c为空气中的声速;V为声腔体积;A为声腔表面积;L为声腔周长。
当结构子系统2为各向同性均质板时,其模态密度为[10]
(3)
式中:Ap为表面积;m为面密度;D为弯曲刚度,其表达式为D=Et3/[12(1-ν2)],其中E为弹性模量,ν为泊松比。
(2) 临界频率
在三子系统SEA模型中,临界频率与子系统2的结构声辐射和隔声性能联系密切,影响最终声振响应结果。子系统2的临界频率为[11]
(4)
(3) 内损耗因子
内损耗因子是指单位频率及单位时间内子系统耗散的能量与其平均储存能量的比值,表明其对振动能量的耗散能力。各子系统内损耗因子取值如图3所示,其中子系统2的损耗因子的名义值由参考文献[12]给出,声腔损耗因子由混响时间求得[13]
(5)
式中:Tcav为混响时间。
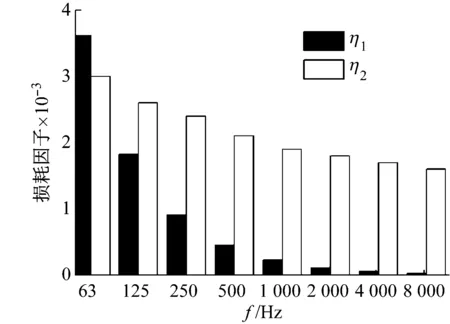
图3 板件与声腔损耗因子Fig.3 Damping loss factor of panel and cavity
(4) 耦合损耗因子
耦合损耗因子表征子系统间的耦合程度,其数值反映子系统间能量流动的能力。虽然从图1直观上看,声源室和接收室没有直接耦合连接,但子系统1通过子系统2的共振模态群与子系统3传递能量。除此之外,子系统1还通过子系统2的非共振模态群与子系统3建立联系(图2中虚线)。两类耦合损耗因子取值如图4所示,其中使用传递损耗求解非共振模态耦合损耗因子η13[14]
(6)
式中:TL13为均质板的隔声量。依据大量隔声试验研究获取无规则入射条件下隔声量经验公式如下[15]
TL13=18lg(m)+12lg(f)-25
(7)
接收室与声源室的声场介质相同,板件与两侧声腔的耦合损耗因子可由辐射效率求解,隔板与声场的耦合损耗因子为
(8)
式中:M为板件质量;σrad为辐射效率,其表达式为
(9)
式中:λc为板件临界频率下波长,P是板件周长。其中
(10)
(11)

图4 非共振与共振耦合损耗因子Fig.4 Coupling loss factor of resonance and non-resonance transmission
1.3 目标函数
引入两个目标函数,分别为噪声降低量和传声损失。其中声源室1与接收室3的噪声级的差值为噪声衰减量-NR(Noise Reduction)
(12)
基于双房间法的隔板传声损失-TL(Transmission Loss)由下式给出
(13)
2 全局灵敏度分析
2.1 方差灵敏度分析法
方差灵敏度分析法由Sobol[16]提出,此类方法基于高维模型展开与方差分解,利用方差描述模型输入变量以及输出响应的不确定性间的关系,将n维模型响应函数的输出方差分解成2n-1个偏方差项,量化每个输入参数对输出参数总体方差的贡献程度以实现全局灵敏度分析。将模型输入参数和不同中心频率分别记为向量x和f,从而SEA三子系统模型简写为
y=f(x,f)
(14)
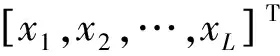

(15)
在f0为常数、输入变量相互独立、函数f平方可积且展开式每项均值为0的条件下,展开式所有项每两项相互正交,且可唯一确定
f0=E(Y)
(16)
fi=E(Y|Xi)-f0
(17)
fij=E(Y|Xi,Xj)-fi-fj-f0
(18)
对展开式两边取方差有
(19)
式中:一阶偏方差Vi=Varxi(E-xi(Y|Xi)),-xi含义为除xi的其他所有变量;二阶偏方差Vij=Varxij(E-xij(Y|Xi,Xj))-Vi-Vj。标准化即可得到一阶灵敏度系数(主效应指标)
(20)
2.2 傅里叶幅值灵敏度检验法
傅里叶幅值灵敏度检验法是全局灵敏度指标计算的典型方法。其基本原理是利用搜索曲线在输入参数多维空间内搜索,将积分由多维转为一维;引入独立参数,对输入参数给定单独频率,使目标函数转变为独立参数的周期性函数;利用傅里叶分析获取模型输出的方差以及对应输入参数的主效应等全局灵敏度分析衡量指标[17]。对于SEA模型中的输入参数x=[x1,x2,…,xL]T,归一化输入参数并引入独立变量s,则输入参数的变换函数为
x′(s)j=g|(sinωjs)
(21a)
式中:x′(s)j为输入结构参数xj的归一化标准量且为变量s的函数,gj为搜索曲线函数。ωj为输入结构参数xj的对应振荡频率。在gj函数下,当变量s变化时,所有的输入参数将在M维空间中沿着一条曲线同时变化。搜索函数选用Saltelli等[18]提出的
现在司乘人员只需用手机扫描二维码,即可完成路政赔补偿款支付,这不仅有效解决了司乘人员因现金零钱不足而不能支付的燃眉之急。同时也减少了基层工作人员辨别真伪和置换零钱的工作量。节省了双方时间,也大大提高了工作效率和工作质量。
(21b)
其中,变量s在[-π,π]内变化,φj为[0,2π]间的随机相位。
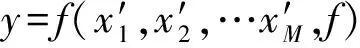

(22)
由于y=f(s,f)是周期为2π的函数,展开成傅里叶级数形式
(23)
式中:b0,bm和cm为傅里叶系数。其中,E(y)=b0/2,bm和cm的表达式分别为
(24)
(25)
因此,模型输出y的方差为
(26)
3 统计能量声振模型全局灵敏度分析
3.1 模型参数
设定目标函数为63~8 000 Hz宽频带下噪声降低量与传声损失,以声腔损耗因子、板件损耗因子,共振模态耦合损耗因子、非共振模态耦合损耗因子为SEA模型输入参数,利用FAST法进行声振响应模型全局灵敏度分析。每个频段下各参数的名义值由1.2节求解,不确定度为10%,概率分布为均匀分布,参数概率分布及不确定度取值情况如表2所示。
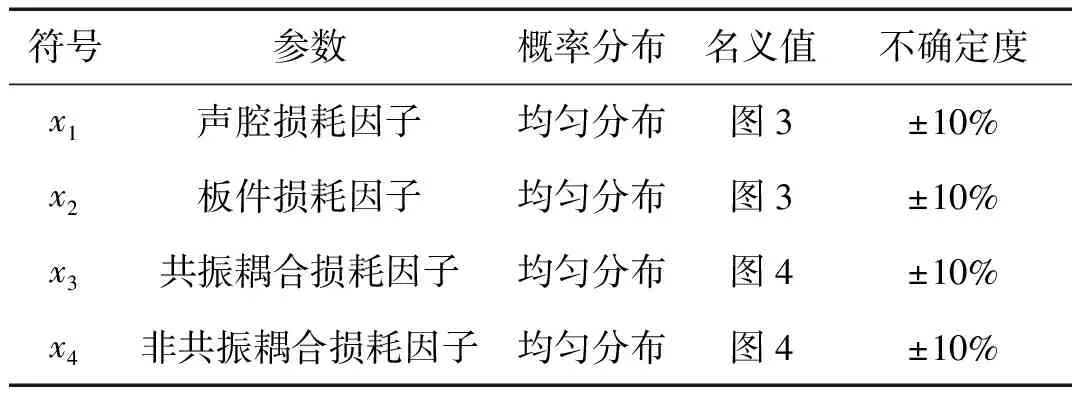
表2 SEA模型参数概率分布及不确定度取值情况表Tab.2 The probability distribution and uncertainty of SEA
3.2 结果分析
统计能量分析模型输入参数的主效应是该参数不确定性对模型输出不确定性作用的量化指标,表明各个输入参数的不确定度传递给声振响应结果不确定度的能力,可用于明确各频段下各参数不确定性的贡献排名。三子系统SEA声振响应模型宽频带噪声衰减量及传声损失的主效应计算结果如图5、6所示。提取噪声衰减量的不同频段下主效应指标,从图7可以看出,最主要的参数为共振传递下的声腔-板件耦合损耗因子,不同频段下灵敏度值在0.40~0.65间浮动,对声振响应的不确定性影响最大。出现这种现象的原因在于三子系统模型中声腔间的共振模态能量流动起主导作用,能量耗散能力远大于板件损耗因子及非共振模态损耗阻尼的作用。虽然其数量级为10-3,但参数估计的准确程度对声振响应结果影响巨大。

图5 噪声衰减量主效应指标Fig.5 Main effect of noise reduction

图6 传声损失主效应指标Fig.6 Main effect of transmission loss
板件内损耗因子在63 Hz的低频段灵敏度值达0.33,但随着频率的上升,其影响能力逐渐下降,并在500 Hz左右被声腔损耗因子超过。但在临界频率2 000 Hz频段下,x2和x1的灵敏度值出现突变,不再遵循其整体趋势规律。原因在于临界频率下,“吻合效应”使得板件的声辐射能力大幅提高,板件自身阻尼损耗及共振传递耦合损耗对接收室声压级的影响降低,而子系统3声腔损耗因子对声振响应的影响能力提升。
非共振传递下的耦合损耗因子仅在低频段有较低的影响能力,且随着频率的升高,其灵敏度值趋于0。在减振降噪设计过程中,可忽略其对声振响应结果不确定性的影响,达到简化设计流程,提高求解效率的目的。
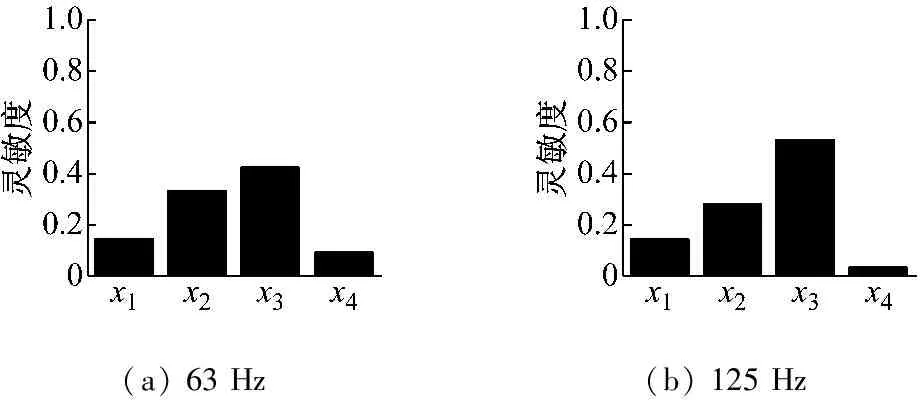
(a) 63 Hz(b) 125 Hz

(c) 250 Hz(d) 500 Hz
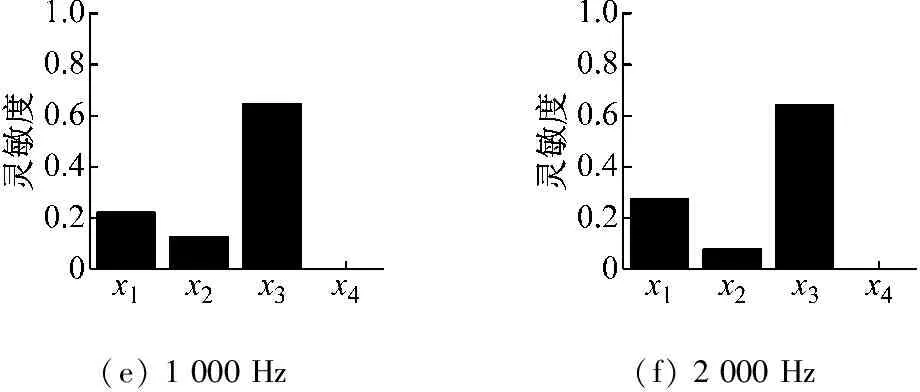
(e) 1 000 Hz(f) 2 000 Hz

(g) 4 000 Hz(h) 8 000 Hz
图7 宽频带统计能量模型噪声衰减量主效应指标
Fig.7 Broadband main effect of SEA model on noise reduction
4 结 论
本文采用傅里叶幅值灵敏度检验法对三子系统统计能量声振模型进行宽频全局灵敏度分析,得到一些对基于统计能量分析原理的声振响应计算与减振降噪优化设计有参考价值的结论:
(1) 宽频带内共振传递下的耦合损耗因子对目标函数的声振响应结果影响最大,是输出函数不确定性的最重要影响参数。
(2) 非共振传递下的耦合损耗因子仅在低频范围内存在一定影响能力,在减振降噪优化设计过程中,可忽略其不确定性对声振响应结果不确定性的影响。
(3) 吻合效应改变临界频率下各参数的灵敏度指标分布情况。板件自身阻尼损耗不确定性对声振响应结果不确定性的影响能力下降,而声腔损耗因子的影响能力提升。
