新型恒扭矩工具动力学模型与降黏机理研究

田家林，张堂佳，程文明，袁长福，杨 琳，董 燚，林晓月(.西南石油大学 机电工程学院,成都 60500；.西南交通大学 机械工程学院,成都 600；.重庆海德世拉索系统

(集团)有限公司,重庆 401120)

钻柱黏滑作为钻柱动力学的一个重要组成部分，一直是钻井工程的研究热点，对钻柱黏滑的现有研究包括描述其动力学特性的数学模型，或者通过实验室或现场测试，分析黏滑规律以及重要参数对其动力学特性的影响[1-5]。这些研究对于探索钻柱黏滑规律，奠定钻柱动力学基础具有重要参考意义。

从工程应用角度而言，钻柱黏滑是导致钻具性能下降，乃至使用寿命迅速降低的重要因素。随着油气资源开采难度的增加，超深井、导向井等各种复杂井身结构的应用越来越多，在这些复杂井身结构与井下工况的条件下，更容易产生比较严重的钻柱黏滑，导致井下事故，影响生产效率与安全。因此，进行复杂井身结构条件下钻柱黏滑理论研究的同时，进行降黏技术研究同样具有重要的意义。为了减小钻具黏滑，国内外相关领域研究机构与学者进行了大量的研究[6-10]，以期实现减轻黏滑、提高效率、达到安全生产的目的。各种降黏工具结构形式差别较大，但就工作原理而言，一种重要的类型是利用轴向振动与扭转振动耦合，通过纵向动力学特性，改变钻具扭转输出性能，从而实现降黏的目的[11-13]。但对于这种基于恒扭矩工具的降黏技术研究，文献调研结果表明，主要集中在实验室或现场测试上，这些研究成果固然具有重要参考价值，但对于相关技术的进一步深入研究，或者优化设计，则缺乏理论支撑，成为制约相关技术突破的瓶颈。

基于此，本文研究的创新点在于以一种新设计的降黏工具(以下简称恒扭矩工具)为载体，结合钻井过程中的实际工况，建立基于纵向与扭转振动耦合的黏滑过程动力学模型，再结合所设计的恒扭矩工具进行算例分析，分析其降黏效果。所建立的分析模型通过部分参数的修正，可用于类似的降黏滑技术。研究成果可为类似技术的深入研究、优化设计、关键参数的定量分析提供理论参考。

1 理论模型

恒扭矩工具结构如图1所示，其工作原理为：该工具实质上是利用其螺旋传动部分使钻头扭转运动转化为轴向移动(超过预设扭矩时)的机械结构，当钻头钻进遇到软硬交错的地层时，结合碟簧系统储存和释放钻井过程中产生的能量，该工具可以自动对钻头破岩过程进行有效控制，减轻甚至消除在复杂地层中由钻头引起的扭转黏滑振动。在钻头上移运动阶段，钻头受到井底反扭矩增大，超过工具的预设扭矩，引起与钻头相连的螺旋芯轴转速小于螺旋壳体产生转速，钻头被逐渐提离井底，钻头的钻压立刻降低使钻头切削齿吃入地层的深度减少，受到的井底反扭矩随之减小，压缩碟簧系统，储存能量，直至钻头恢复全速运动状态；钻头下移运动阶段，由于碟簧系统处于被压缩状态而释放能量，使螺旋芯轴转速大于螺旋壳体转速，利用螺旋传动部分，使钻头轴向下移，继续吃入岩层破岩，从而减小了扭矩波动，钻头将始终保持相对恒定转矩平稳地钻进。

1.上接头;2.中心管;3.碟簧系统;4.上壳体;5.防掉接头;6.螺旋壳体;7.螺旋芯轴

图1 恒扭矩工具示意图
Fig.1 Schematic diagram of constant torque tool

通过现场实践发现，钻柱系统在深井、超深井中经常会受到黏滑振动，而黏滑振动的主要破坏形式是引起钻柱系统强烈的轴向和扭转振动[14-17]。

为了深入了解工具黏滑作用机理，根据恒扭矩工具的工作原理，建立如图2所示的有恒扭矩工具作用时的钻柱模型[18-21]。

图2 含有恒扭矩工具的钻柱系统模型示意图Fig.2 Schematic diagram of drill string system with constant torque tool

图2中底部钻具组合被分为两部分：第一部分为恒扭矩工具上部，具有质量惯性矩I和集中质量M；第二部分为恒扭矩工具下部，具有质量惯性矩Ib和集中质量Mb。钻柱系统坐标由下式给出

q=[UUbφφb]T

(1)

式中:U,φ分别为恒扭矩工具上部轴向位移、角位移；Ub,φb分别为钻头部分轴向位移、角位移。

为体现恒扭矩工具中螺旋部分轴向位移和扭转角位移之间的耦合运动，引入运动约束。该运动约束方程由螺纹导程Ph、螺纹升角λ之间的关系得出

(2)

为得到包含恒扭矩工具作用的钻柱系统运动学方程，采用具有约束系统的拉格朗日方法，其一般形式为

(3)

式中:Ek为系统动能；Ep为系统势能；(Qnc)为非保守广义力；λ1为与式(2)中约束相关的广义约束力。

钻柱系统的动能为

(4)

钻柱系统的势能为

(5)

非保守力和扭矩为

(6)

将式(2)写为h(q)=0的形式

h(q)=Ub-U+α(φ-φb)

(7)

将式(7)对坐标系统求导可得

(8)

在钻头滞动时，钻头动能为0，则有

(9)

(10)

(Wλ1)T=[-λ1λ1αλ1-αλ1]T

(11)

将式(9)～(11)代入式(3)的拉格朗日方程得到

(12)

根据式(2)得到

(13)

(14)

将(14)代入(12)中消除与φ相关的自由度，得到具有无约束3自由度的恒扭矩工具钻柱系统模型运动学方程如下

(15)

(16)

1.1 正常滑动阶段

结合无恒扭矩工具作用时钻头正常滑动阶段运动特性，得到有恒扭矩工具作用下钻柱系统的扭转和轴向运动关系如下所示

(17)

初始运动的边界条件为

(18)

1.2 上移阶段

当钻头钻进到软硬交错的岩层区，钻头受到的反扭矩增加到Tre(max)，钻头的转速逐渐减小。若Tre(max)>T1，钻头与恒扭矩工具外螺旋线芯轴的转速小于恒扭矩工具内螺旋线本体的转速，此时钻头轴向上移。

在钻头上移过程，钻头吃入岩层的深度减小，钻头受到的反扭矩Tre(max)和钻压W(max)也逐渐减小。根据式(15)得到钻头上移过程中的运动方程

(19)

其中

(20)

(21)

钻头开始上移的瞬间，初始边界条件为

(22)

随着钻头的上移，外螺旋线芯轴轴向压缩碟簧系统，碟簧产生的轴向压力逐渐增加，当Tre(max)=T11时，外螺旋线芯轴再次与内螺旋线芯轴一起等速转动，钻头停止轴向上移，此时的时间为t2。

1.3 下移阶段

当T12>Tre，碟簧系统开始逐渐释放轴向压缩量，使外螺旋线芯轴开始带动钻头轴向下移并加速转动。结合式(15)，得到钻头下移过程的运动方程

(23)

其中

(24)

钻头开始下移瞬间，钻头运动初始边界条件为

(25)

随着钻头的下移，碟簧产生的轴向压力逐渐减小，Tre逐渐增加，当T12=Tre时，外螺旋线芯轴的转速等于钻柱的转速，外螺旋线芯轴带动钻头与钻柱一起旋转，进行正常钻进。

2 算例分析

根据上述的结构设计方案，设计出172 mm恒扭矩工具，为了解具有恒扭矩工具与无恒扭矩工具的钻柱系统在运动过程中的黏滑特性，根据表1中的相关数据，以及上面相关过程的运动方程，利用数值编程对有/无恒扭矩工具作用时钻头的周向转动和轴向运动进行对比分析，得到不同的对比分析结果。

表1 恒扭矩工具相关计算参数Tab.1 Calculation parameters of constant torque tools

2.1 无恒扭矩工具时的钻头扭转与轴向运动

根据无恒扭矩工具的钻柱模型，得到钻头从正常岩层区域-软硬交错的黏滞岩层区-脱离黏滞区的周向转动角位移、角速度与轴向位移、轴向速度的变化过程，如图3(a)和(b)所示。在前t=100 s内，钻头处于正常钻进阶段；在t=100 s后，钻头进入软硬交错的岩层区域，由于软硬交错层岩层的强度、摩擦力等增加，钻头进入黏滞阶段，转动角速度、轴向钻进速度迅速减小。图3(a)中，在t=100.5 s时，钻头驱动扭矩不足以克服岩层的反扭矩Tre(max)时，钻头转动角速度变为0，钻头进入滞动阶段；而图3(b)中，在进入黏滞区域瞬间，钻头的轴向钻进速度已经变为0。在滞动阶段，钻柱的转动角位移与轴向位移保持不变；由于钻柱顶端持续以恒定转速Ω0=2π rad/s转动，施加在钻头上的驱动扭矩逐渐累积增加，在t=103.5 s时，钻头上积累的能量大于Tre(max)后，钻头滑脱。在钻头滑脱后，钻头转动角速度与轴向下移速度迅速增加，最大值分别达到了15.47 rad/s、0.036 61 m/s。在大幅波动后，随着钻进的进行，钻头重新回到稳定钻进阶段。

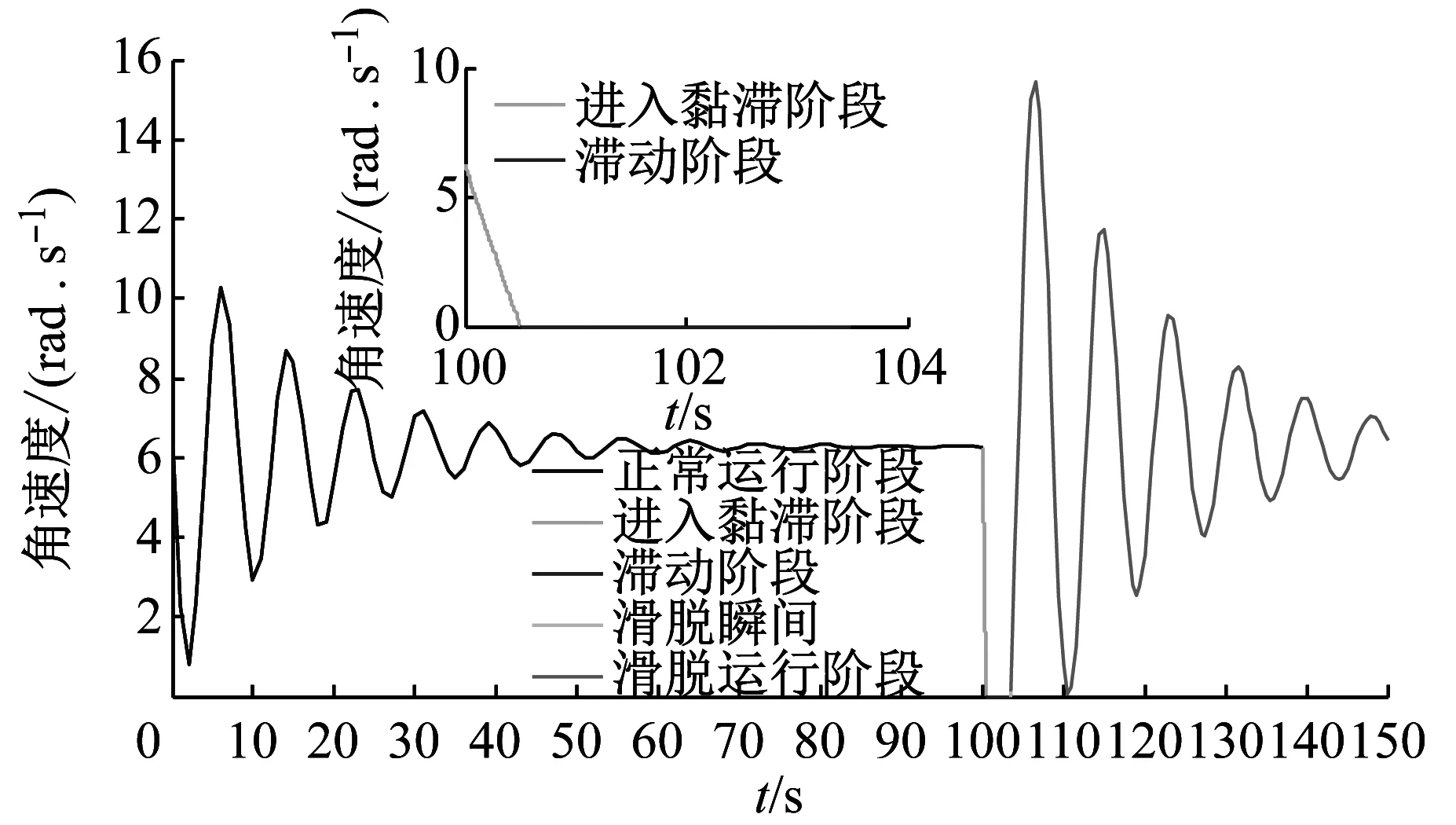
(a)无恒扭矩工具时钻头扭转运动结果

(b)无恒扭矩工具时钻头轴向运动结果

2.2 有恒扭矩工具时的钻头扭转与轴向运动

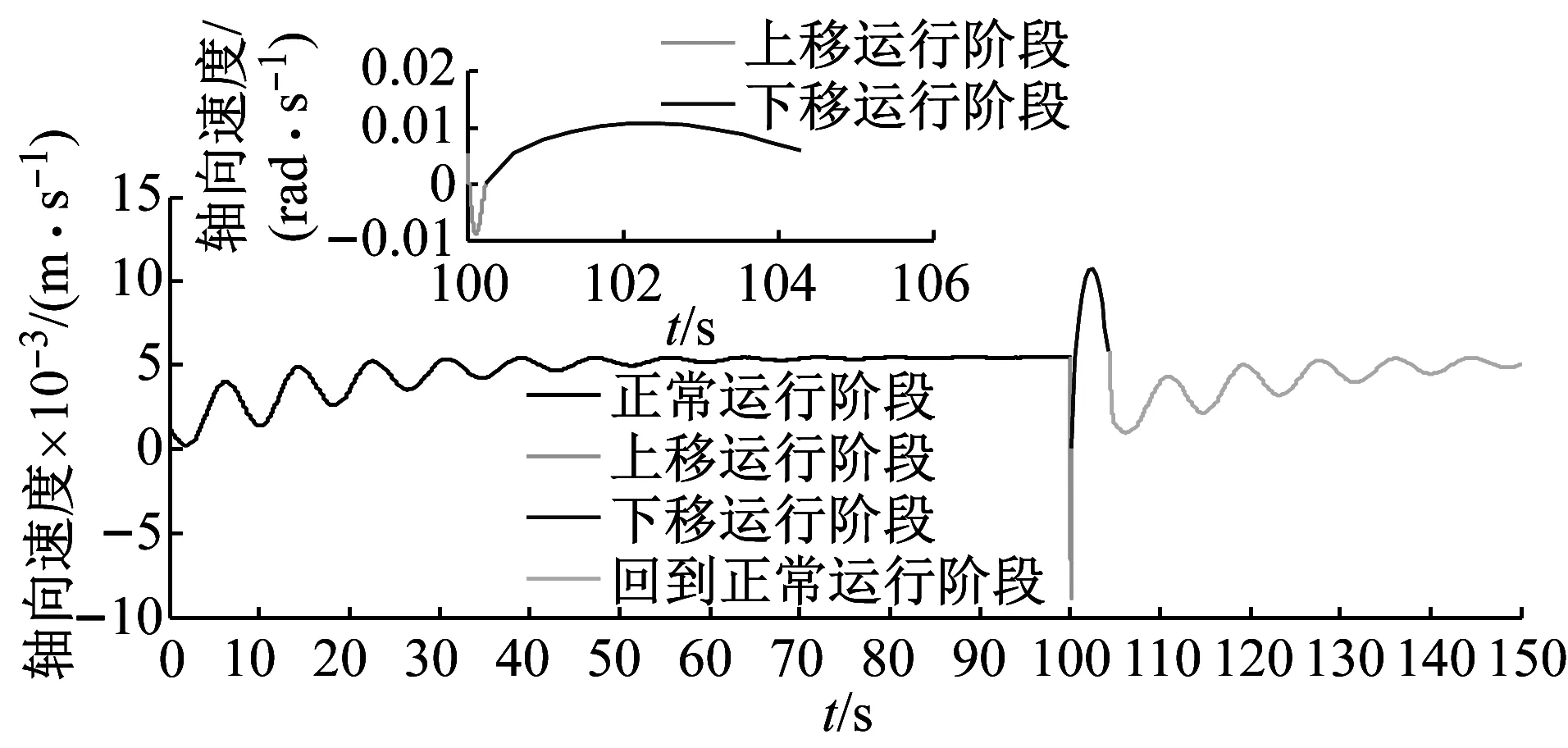
根据含有恒扭矩工具的钻柱模型，得到钻头钻进过程中周向转动角位移、角速度与轴向位移、轴向速度的变化，如图4(a)和(b)，在前100 s中的正常钻进阶段，与无恒扭矩工具的钻柱模型一致。在t=100～100.23 s为钻头轴向上移阶段，此阶段钻头钻进到软硬交错的岩层区域，导致钻头受到岩层的阻力增加。由于此时的Tre(max)>T1，钻头转速减小，使钻柱与钻头之间产生转速差，通过恒扭矩工具螺旋副的作用，钻头逐渐被提起并压缩恒扭矩工具的碟簧。钻头上移过程中，吃入岩层的深度逐渐减小，Tre(max)、W(max)也逐渐减小，T1逐渐增加，当t=100.23 s时，钻头上移位移达到最大值5.5 mm(恒扭矩工具行程达到最大值)。此过程中，钻头的轴向上移速度从0.005 465 m/s迅速减小，然后增加到0 m/s。在t=100.23 s，钻头结束上移运动的同时脱离了软硬交错的黏滞区域，钻头的受力迅速减小，在恒扭矩工具碟簧力的作用下，钻头加速转动并加速下移。钻头下移钻进过程中，Tre、W逐渐增大，T12逐渐减小；在t=104.37 s时，恒扭矩工具行程变为0，此时的Tre=T12，钻头轴向移动速度和周向转动速度再次趋于稳定状态。

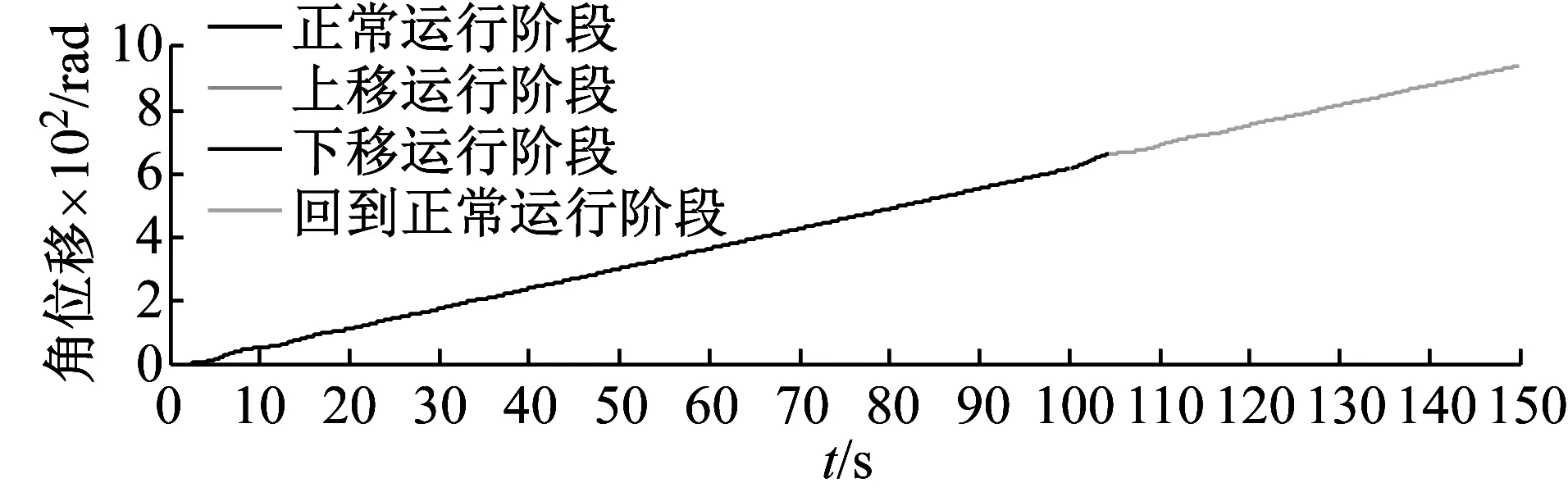
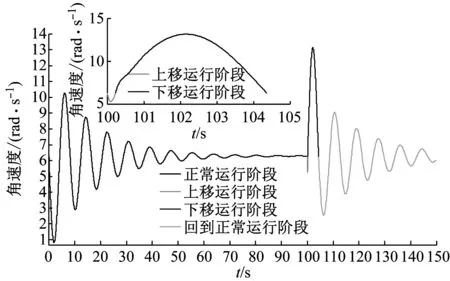
(a)恒扭矩工具作用下钻头扭转运动结果

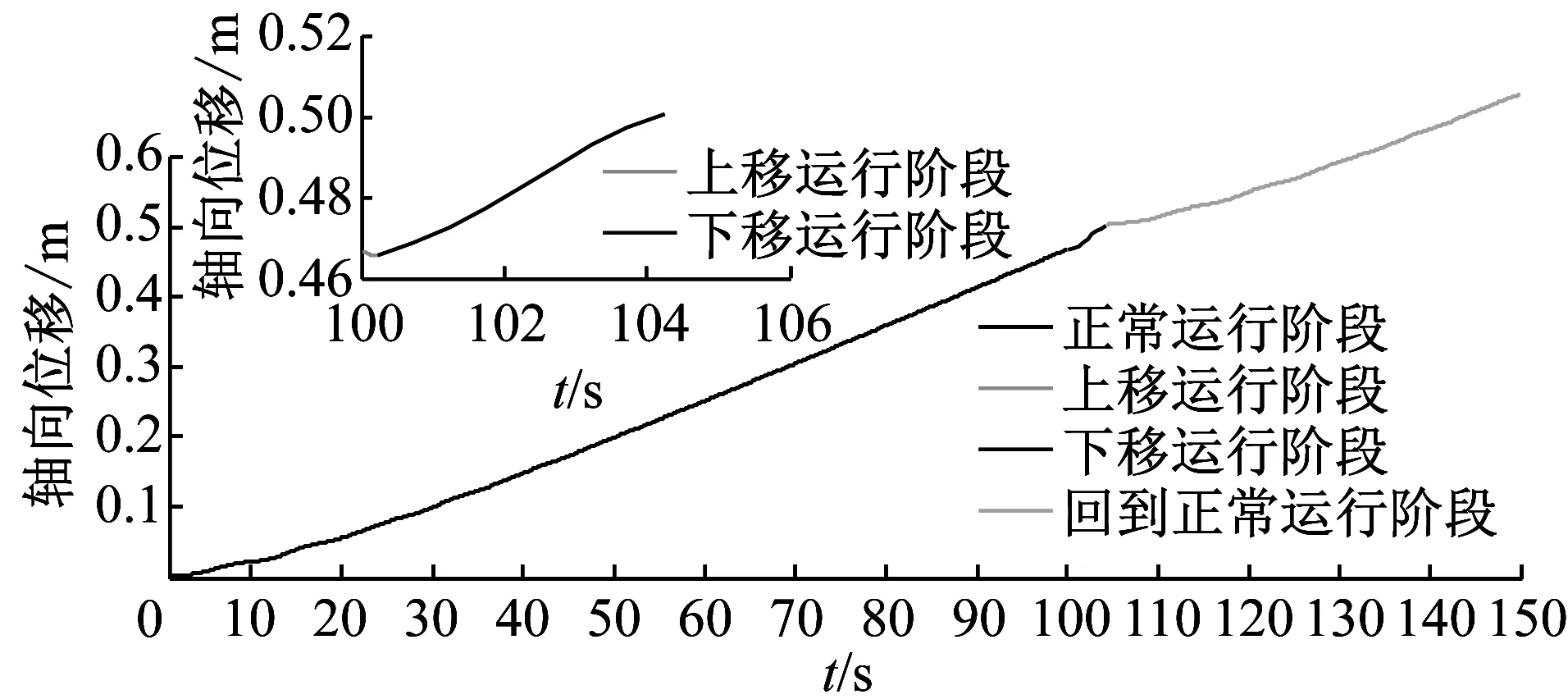
(b)恒扭矩工具作用下钻头轴向运动结果

对比图3、图4发现：含有恒扭矩工具的钻柱模型在进入软硬交错的岩层区域时，钻头没有出现卡钻、滞动的运行情况，在钻头上移、下移运行过程中，钻头保持着较高的转动角速度，整个运行过程中钻头轴向与周向运动速度较为平稳。

2.3 有/无恒扭矩工具时的钻头扭矩与钻压

对比图5(a)和(b)发现：具有恒扭矩工具作用时，钻头上的扭矩在整个过程中波动范围较小，最大波动幅度约为2 512 N·m；而无恒扭矩工具作用时，钻头上的扭矩在滞动过程中出现大幅增加，最大波动幅度约为7 154 N·m，滑脱后扭矩波动频率较快和波动幅度较大。在钻压变化方面，有恒扭矩工具与无恒扭矩工具的钻头在整个运行过程中，钻压波动幅度基本一致；而在进入黏滑区域后，有恒扭矩工具的钻压增减变化频率快于无恒扭矩工具的钻头钻压。

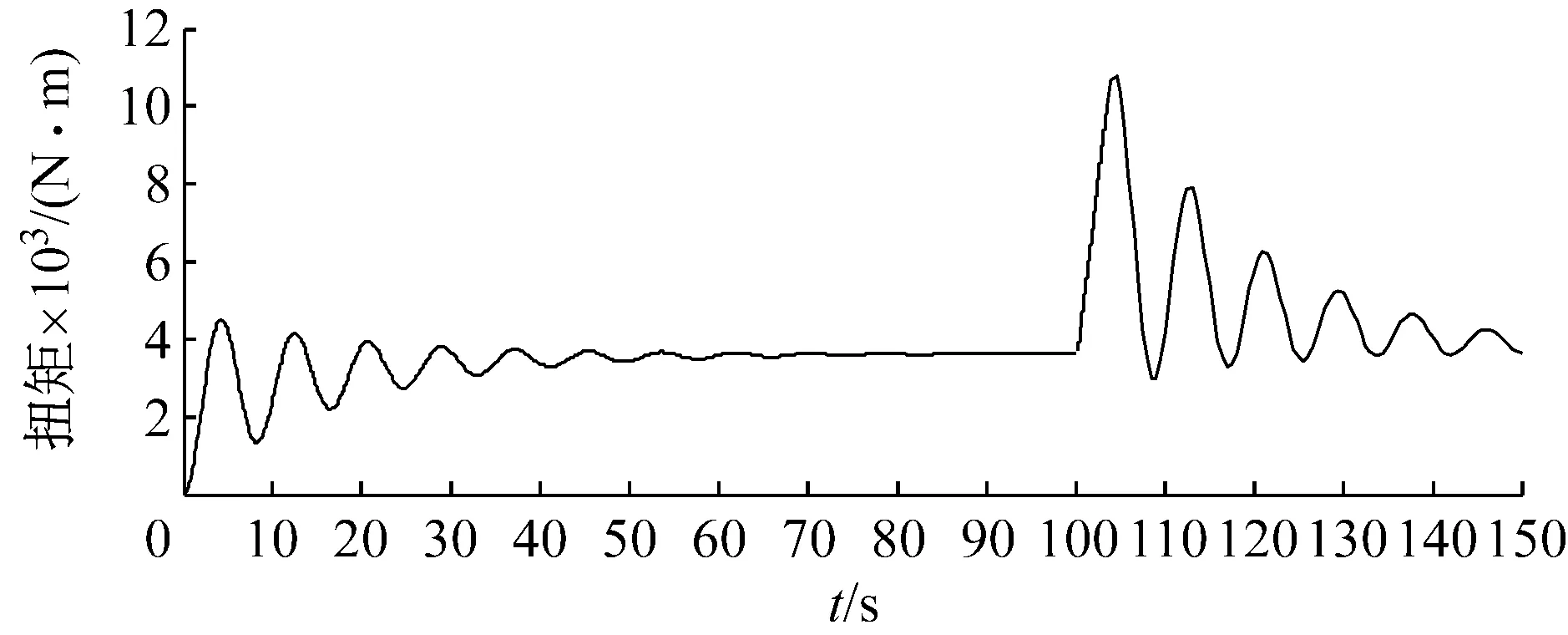
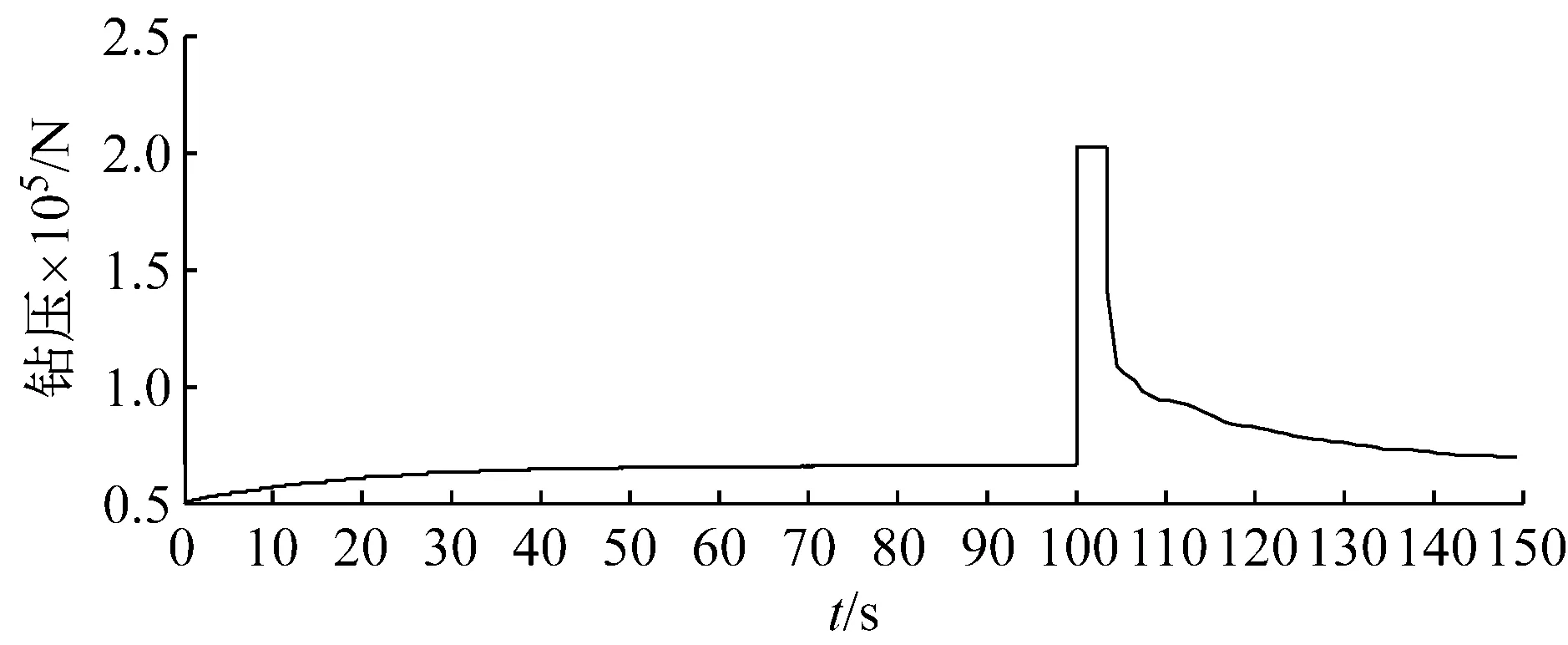
(a)无恒扭矩工具作用

(b)恒扭矩工具作用

3 现场实验

为验证理论模型与计算方法的正确性，进行现场实验测试与分析，对测试结果与理论计算结果进行对比分析。首先基于算例分析中的恒扭矩工具参数，进行相应结构尺寸的恒扭矩工具加工制造，对应的工具实物图如图6所示。然后选择一口预探直井进行现场实验，在上沙溪庙、下沙溪庙、千佛崖及自流井马鞍山段采用PDC+Ø172 mm恒扭矩工具钻进，分三趟钻进，钻进井段3 151.20～3 603.30 m，总纯钻时间219 h，平均机械钻速2.06 m/h。其中，现场实验的井身结构如图7所示，实验过程参数记录如表2所示。

图6 恒扭矩工具图Fig.6 Constant torque tool photo

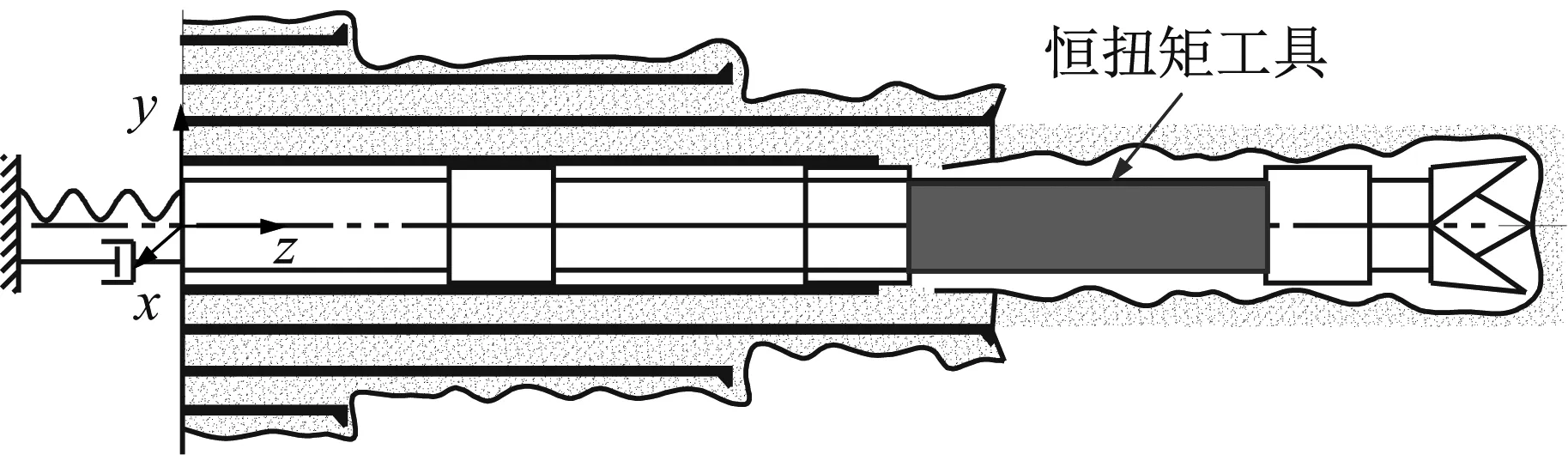
图7 井身结构示意图Fig.7 The structure of the drilling wellbore

表2 恒扭矩工具使用统计表Tab.2 Constant torque tool usage statistics table

实验过程中，为了进行对比验证，在钻进到3 603.30 m时，起钻卸掉恒扭矩工具，继续钻进。现场录井数据如图8所示。由图8可得，在使用恒扭矩的井段3 151.20～3 603.30 m，扭矩波动范围为1.46～5.56 kN·m，平均扭矩为3.06 kN·m，在误差范围内，与理算计算稳定扭矩相符合，验证了理论模型、求解方法以及算例分析的正确性；而在未使用恒扭矩的井段3 603.30～4 037 m，扭矩波动范围为0.53～7.96 kN·m，平均扭矩为4.14 kN·m，由此可见，应用恒扭矩工具段与不带工具段相比扭矩波动小而平稳，黏滑振动减轻。

图8 应用恒扭矩工具前、后扭矩随井深变化曲线Fig.8 Torque curve along the well depth before and after application of constant torque tool

4 结 论

(1)本文通过建立基于扭转与纵向振动耦合的恒扭矩工具钻柱黏滑振动模型，结合工程背景，建立其动力学分析模型，根据设计参数及工況参数，进行算例分析与现场实验。结果表明：建立的理论模型与计算方法紧密结合实际工程背景，可为类似的降黏滑、恒扭矩技术提供理论基础。

(2)文中所提出的恒扭矩工具通过螺旋传动与碟簧的结合实现纵扭耦合，能够提高钻头工作稳定性。从经济性而言：恒扭矩工具通过实时自动调整钻进扭矩来动态平衡井下扭矩，降低扭矩波动范围，降低黏滑，提高机械钻速，可极大地提高勘探开发钻井的经济性。从安全生产而言：恒扭矩工具能够减少井下钻柱卡滑憋跳现象，减轻钻柱黏滑振动，在钻井过程中减少剧烈冲击，有效保护井下钻具组合。

(3)钻柱动力学作为钻井工程的中枢神经，其研究发展是油气资源开采的关键，随着能源格局的变化，新型油气资源对应的开采条件，使得减摩降阻、降黏恒扭、提速增效技术对于节能增效、安全环保具有更重要的社会意义。基于本文提出的理论模型与工具设计，进一步进行高效稳定的恒扭矩、防滞动技术研究，对新形势下的能源技术开采具有重要意义。