悬吊式模态试验系统基频测试误差分析

吴 松，郭其威，臧 旭，徐 腾

(1.上海宇航系统工程研究所，上海 201109; 2.上海市空间结构机构重点实验室，上海 201108)

随着航天科技的进步和发展，许多空间科学应用领域对大型可展开天线和柔性电池翼的需求越来越突出，这类结构复杂、柔度大、基频低，动力学特性丰富，与飞行器本体耦合程度严重，为保证飞行器本体在轨姿态控制稳定，对这类大柔性可展开结构基频提出了一定指标要求[1]。因此，为保证这类大型可展开机构在轨状态动力学特性满足设计要求，需在地面开展这类超低频可展机构的模态试验。

传统模态测试考虑到被测结构频率较高，重力对结构频率影响较小，基本都被忽略[2-3]。大型可展开机构，柔性大、频率通常低于5 Hz，重力影响大，传统竖直放置测量基频的方法将会带来较大误差。文献[4-5]根据传统重力影响下的模态测试结果，采用仿真分析方法对试验结果进行修正，消除重力、空气阻力等影响，从而得到无重力影响下的模态测试结果。

超低频模态测试系统采用悬吊方式安装被测产品，补偿重力对产品结构基频的影响，进而开展地面模态试验，测量产品无重力下的模态。然而，由于被测结构基频低，需首先认识悬吊模态测试系统对产品测试频率的影响，以确保悬吊模态测试结果真实可靠[6-8]。

为清楚认识悬吊系统测试结果与产品真实值之间的关系，文章通过对超低频模态试验系统频率测试误差展开理论建模研究，从理论上揭示测试结果与理论值之间产生差异的原因，揭示超低频模态试验系统频率测试误差的影响机理，为后续如何使用试验测试结果提供指导。

此外，文章以梁系结构为研究对象，由于空气阻力对梁系结构模态测试结果影响小，故在下文建模中不考虑空气阻尼影响。但倘若试验产品为大面积帆板或柔性翼等结构时，由于其面积大，空气阻尼对测试结果影响显著，此时不仅需要考虑测试系统的误差，同时要考虑空气阻力的测试误差[9-11]。

1 超低频模态试验系统简介

图1为悬吊式超低频模态测试系统简图，钢丝绳上端与一质量块连接，通过调节气浮装置压力，对质量块施加向上的载荷，以平衡产品重力。其中，质量块仅在垂直方向自由，通过反馈控制会使之与产品一起随动，并保证钢丝绳内张力稳定。

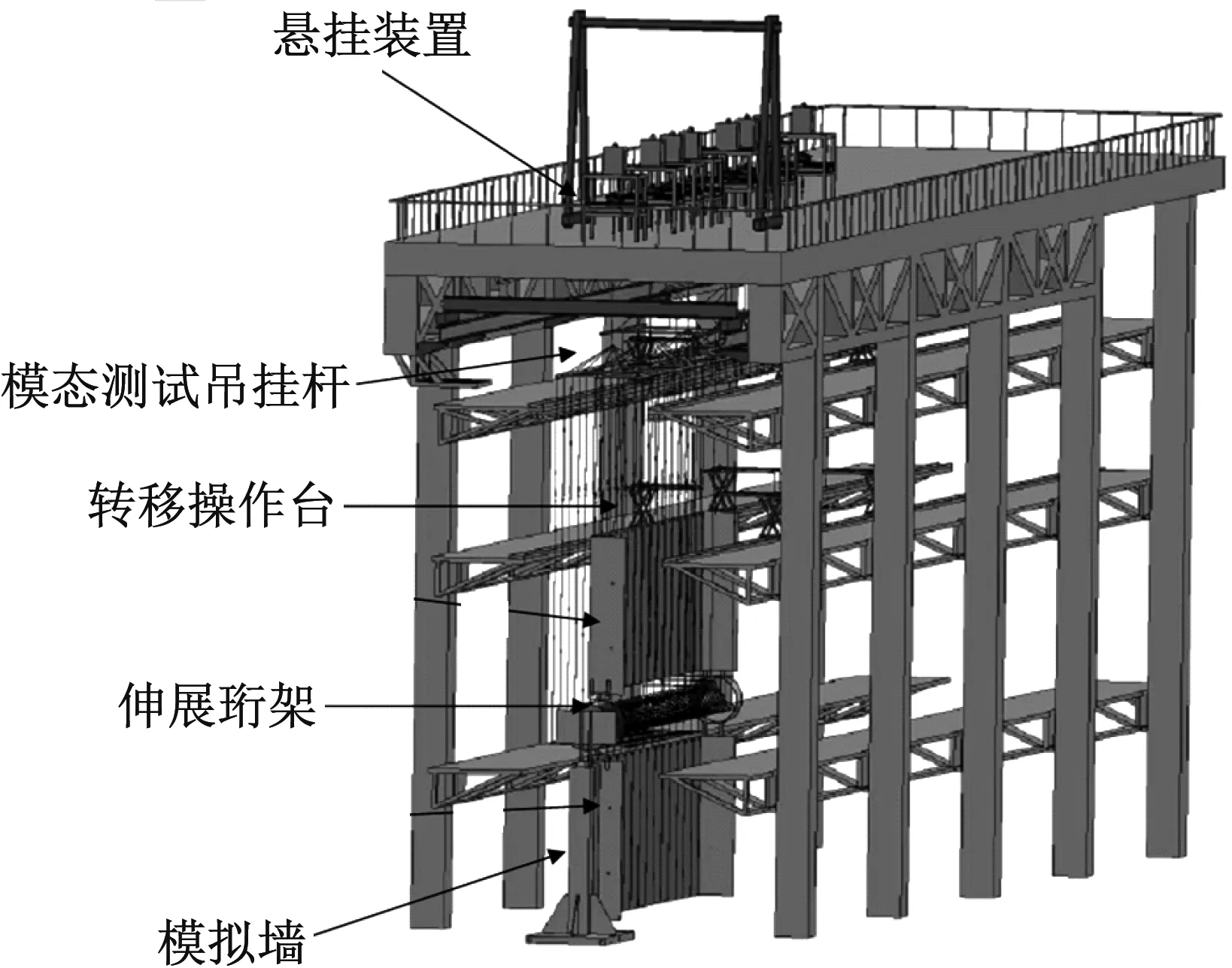
图1 悬吊式超低频模态测试系统Fig.1 The suspended ultra-low frequency modal test system

2 悬吊式超低频模态试验系统频率测试误差分析

根据超低频模态测试系统工作原理，产品在垂直方向测试频率的影响主要受上方质量块和气浮装置的附加影响；水平方向测试频率主要由于悬吊钢丝绳内力在水平方向分量的影响。考虑到悬吊系统对产品在水平和垂直方向频率影响机理的不同，下文对超低频模态试验系统在垂直和水平方向的基频测试误差分别开展研究。

2.1 垂直方向基频测试误差分析

2.1.1 理论模型建立

根据悬吊系统平衡标杆重力的机理，大型可展开机构在垂直方向的频率测试系统可以简化为如下理论模型的系统频率问题。垂直方向理论模型，如图2所示。其中，图示左端边界表示固支边界，下文亦同。

假设在气浮装置控制作用下，钢丝绳上方质量块与产品一起随动，相当于在产品各悬挂点处增加了一个集中质量块，因此，理论模型可以进一步简化为如图3所示带集中质量块的经典频率问题。

图2 垂直方向理论模型Fig.2 Theory model of vertical direction

图3 改进后垂直方向理论模型Fig.3 The improved theory model of vertical direction

2.1.2 理论模型解析解

瑞利法求解图3理论模型基频公式[12-13]为

(1)

代入相应参数，得到理论模型基频解析解为

(2)

式中:ωtest为产品测试圆频率；ωzhen为产品真实圆频率；αi为第i个集中质量块与产品总质量(ρl)的比值；ηi为第i个集中质量点距根部的距离与产品长度的比值，也即Li/L；n为集中质量个数，也即悬吊点个数。

2.1.3 误差分析

为表征悬吊系统对垂直方向基频测试值的影响，引入以下无量纲函数

(3)

该函数建立了垂直方向产品基频测试值与真实基频值、悬吊点个数以及质量块相对产品总质量比值的关系。

假设有n个悬吊点，从端部开始均匀布置，且每个悬吊处上方质量块质量均相同，则产品在垂直方向的基频测试值与真实值的比值为悬吊个数以及单个悬吊集中质量与产品质量比值的二元函数，变化曲线如图4。

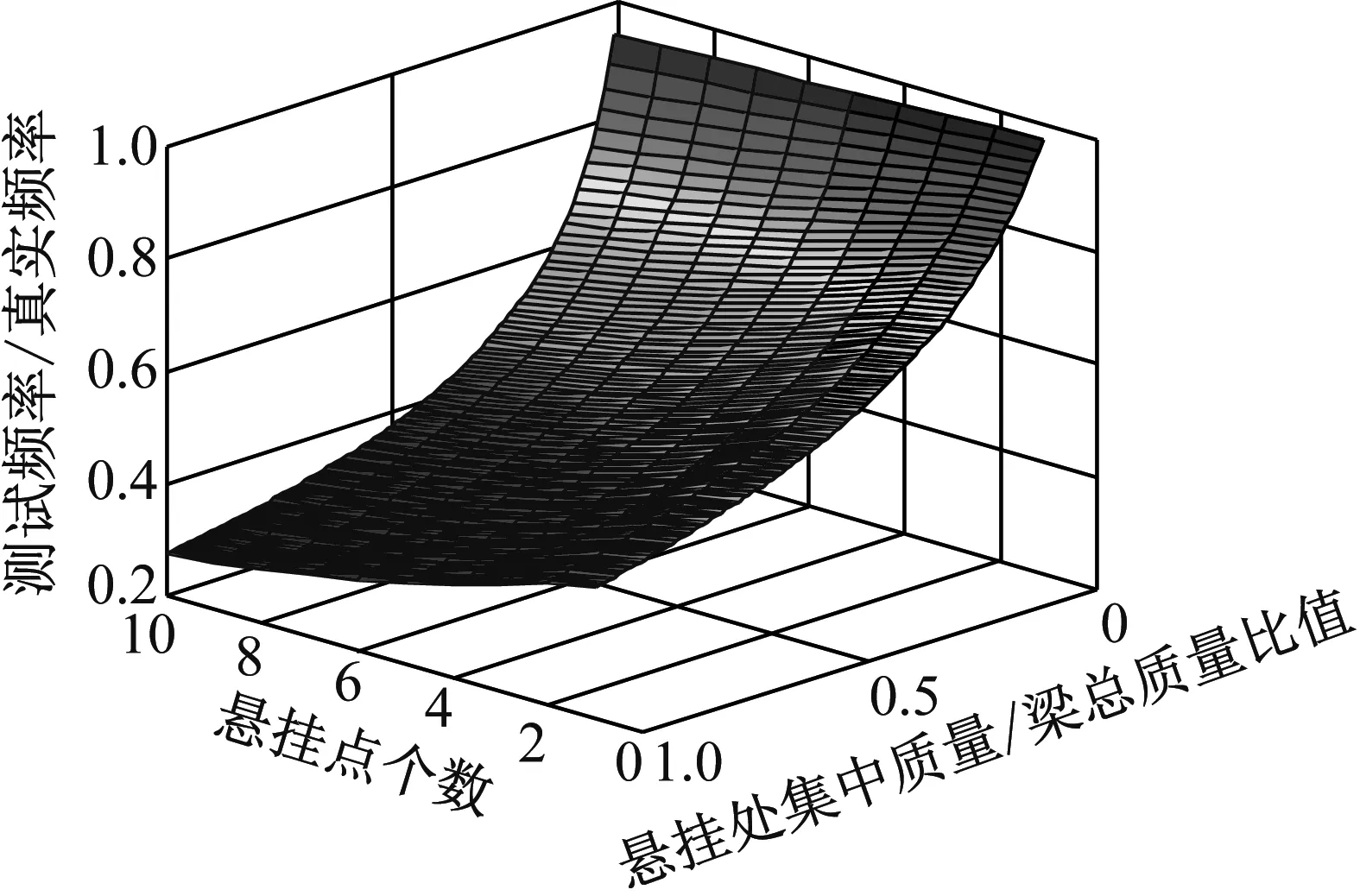
图4 垂直方向频率误差Fig.4 The frequency error of vertical direction

2.1.4 由基频测试值推算真实值

根据理论分析，由于悬吊系统上方质量块的影响，使得产品在垂直方向基频测试值低于真实值。因此，若要得到产品水平方向真实基频值，则需要对基频测试值进行修正，具体步骤如下。

(1) 根据试验状态，确定产品总质量m，吊挂个数n，每个吊挂点处的集中质量与产品质量比值αi，每个吊挂点距根部距离与产品长度的比值ηi；

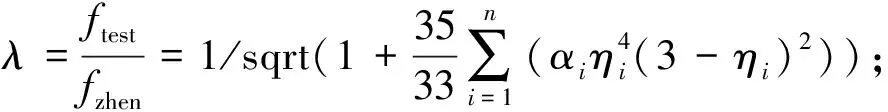
(3) 计算产品垂直方向真实频率，fzhen=ftest/λ。

2.2 水平方向基频测试误差分析

2.2.1 理论模型建立

悬吊系统对产品水平方向频率的影响主要由钢丝绳内张力沿水平方向分量产生，由于气浮平台反馈控制作用，悬吊钢丝绳内张力在平衡内力的同时基本保持不变，假定单根钢丝绳内的张力为T，钢丝绳悬吊高度L0，钢丝绳摆动角度θ，则钢丝绳在水平方向的作用力为

(4)

式中:x为产品在悬吊点处沿水平方向位移，k=T/L0为等效弹簧刚度。

每个悬吊在水平方向对产品的作用，相当于一个刚度为k=T/L0的弹簧，因此，从上俯视视角来看，悬吊式超低频模态试验系统在水平方向系统频率可以简化为如图5所示带弹簧的经典频率问题。

2.2.2 理论模型解析解

瑞利法求解图5理论模型基频公式如下[14]

图5 水平方向理论模型(俯视图)Fig.5 Theory model of horizontal direction

(5)

代入相应参数，得到理论模型基频解析解为

(6)

式中:ωtest为产品测试圆频率；ωzhen为产品真实圆频率；m为产品总质量；L0为悬吊钢丝绳高度；Ti为第i个悬吊钢丝绳内张力；ηi为第i个悬吊点距根部的距离与产品长度的比值，也即Li/L；n为悬吊点个数。

当有无数个吊点时，系统在水平方向可以简化为图6单自由度弹簧振子模型。

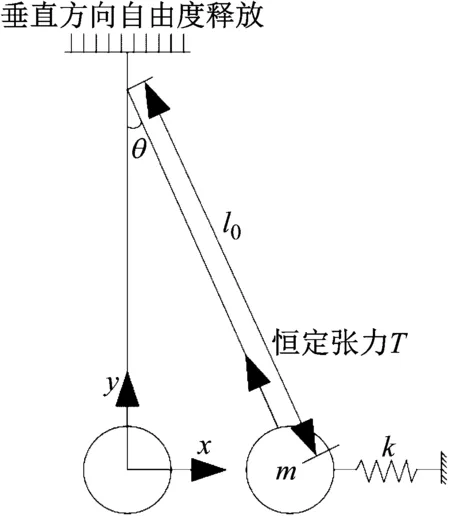
图6 无限多吊点时的理论模型Fig.6 Theory model of infinite lifting point

假设振子作小幅运动，根据牛顿第二定律，该振子在水平方向的动力学方程为

(7)

系统的频率为

(8)

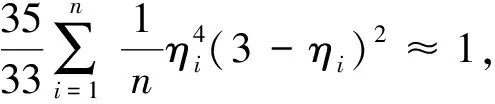
2.2.3 误差分析

为表征悬吊系统对水平方向基频测试值的影响，引入系统误差等效频率

(9)

由式，可知产品基频测试值、基频真实值和系统误差等效频率值有如下关式

f2test=f2zhen+f2ε

(10)

由上式可知，由于悬吊系统影响，水平方向基频测试值偏大，当基频真实值相对于系统误差等效频率值较大时，测试值与真实值相差较小，当产品基频真实值接近或小于系统误差等效频率值时，测试值与真实值之间会产生较大偏差，甚至淹没真实值。

设n个吊点从头部依次均匀布置，即ηi=i/n，且每个吊点处钢丝绳的张紧力为Ti=mg/n，则式变为

(11)

此时，系统误差等效频率为悬挂点个数n和悬挂高度L0的二元函数，变化曲线如图7。

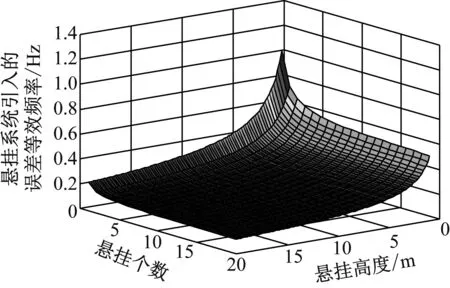
图7 系统误差等效频率曲线Fig.7 The curve of equivalent frequency of system error

2.2.4 由基频测试值推算真实值

根据理论分析，由于悬吊系统钢丝绳内张力的影响，使得产品在水平方向基频测试值大于真实值。因此，若要得到产品水平方向真实基频值，则需要对基频测试值进行修正，具体步骤如下：

(1) 根据试验状态，确定如下参数：① 产品的质量m；② 悬吊高度L0；③ 第i个吊点钢丝绳内张力Ti；④ 第i个吊点距根部距离与产品长度比值ηi=Li/L。

(2) 由式(9)计算产品系统误差频率

(3) 根据基频测试值ftest和系统误差频率fε，由式(10)计算产品水平方向真实频率

fzhen=sqrt(f2test-f2ε)

此外，经计算，当ftest≥3.3fε时，基频测试值与真实值之间的误差小于5%，此时，可以认为测试结果即为真实结果。

3 仿真和试验验证

3.1 试验结果

如图8所示，试验工况说明：图8(a)为2节4 m长的梁竖直状态无悬吊系统的模态试验；图8(b)为2节4 m长的梁水平状态下，一个吊点(端部)下模态试验；图8(c)为8节16 m长的梁水平状态下，4个吊点(图中箭头位置)情况下的模态试验。

为清楚认识悬吊系统频率测试误差，开展了相关标杆试验，验证上述理论分析正确性。试验工况如图8，基频测试结果如表1。其中，单节标杆参数：截面为圆形，外径75 mm，壁厚2.5 mm，单节长2 m，每米重2 kg。

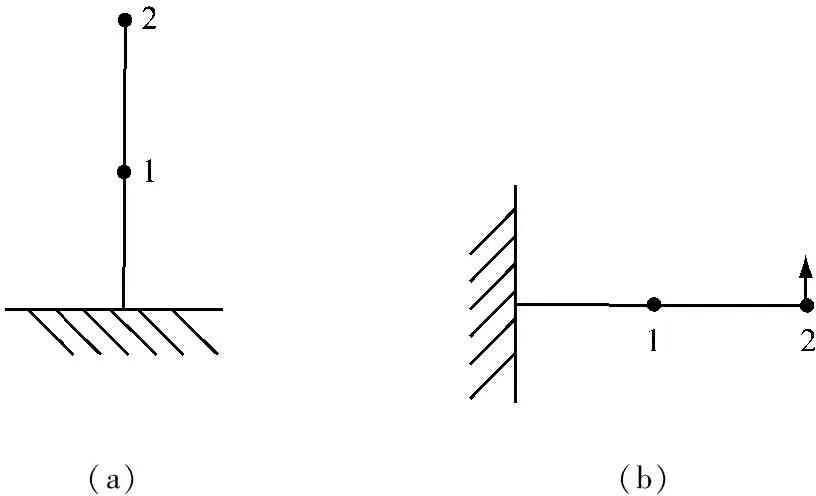
(a)(b)

(c)

表1 标杆频率试验值Tab.1 The test frequency of standard bar

3.2 测试值推算产品真实值

按照2.1.4和2.2.4步骤，根据工况2和工况3悬吊状态以及试验测试结果，推算标杆两个工况下垂直和水平方向的真实基频值，如表2。其中，由于工况1为竖直无悬吊下测试结果，故无推算值。

表2 标杆频率推算值Tab.2 The calculated frequency of standard bar

3.3 标杆基频仿真值

建立相应有限元模型，两个工况下标杆基频仿真分析值如表3。

工况1为竖直状态梁结构有限元模型仿真值；工况2指在仿真模型中引入悬吊系统原理的仿真模型，并根据工况2的实测结果，在仅合理修正梁结构参数条件下，使得仿真值与工况2测试值误差在5%以内，并基于此修正后梁的仿真模型，计算其在无悬吊情况下频率值，即所需要的真实值；工况3中仿真值计算过程与工况2类同。

表3 标杆频率有限元分析值Tab.3 The finite element analysis frequency of standard bar

3.4 结果汇总与对比

对应两个试验工况，汇总标杆基频测试值、推算值和仿真分析值，如表4。

表4标杆基频理论分析值、实测值和有限元分析值
Tab.4Thefundamentalfrequencyofstandardbaroftheoreticalanalysis,testandfiniteelementanalysis

工况方向测试/Hz推算/Hz仿真/Hz误差/%2垂直1.7753.43.5-2.86水平3.303.283.5-6.293垂直0.1660.2080.1966.12水平0.2440.2000.1962.04

两个工况下标杆基频推算值和仿真值吻合得较好，验证了悬吊式超低频模态试验系统理论模型的正确性。

4 结 论

(1) 悬吊式超低频模态试验系统在垂直方向基频测试值小于真实值；水平方向基频测试值大于产品真实值。

(2) 由于附加质量影响，垂直方向基频测试值与真实值相差较大，需要对基频测试值进行处理方能得到准确基频真实值。

(3) 水平方向产品基频测试值、真实值和系统误差等效频率值满足勾股定理公式，且当ftest≥3.3fε时，基频测试值与真实值误差小于5%，此时，可认为基频测试值即为产品真实基频值。