挖掘教材知识,巧用四点共圆解难题
2018-10-18
一、根据教材中圆的定义,判定四点共圆
到定点的距离等于定长的点都在同一个圆上。
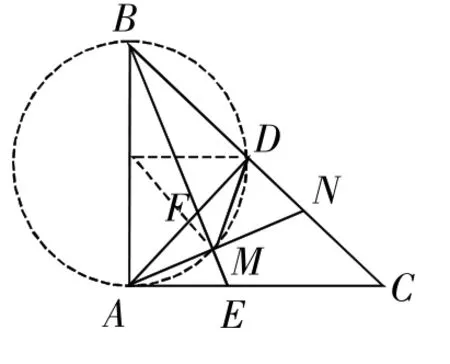
例 1.如图(1),在等腰 Rt△ABC中,∠BAC=90°,AD⊥BC 于点 D,∠ABC 的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连接DM,求∠BMD的度数。

图(1)

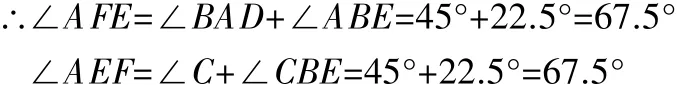

如图(2),取AB的中点O,
图(2)
连接 DO、MO,
∴AO=BO=DO=MO,
∴A、B、D、M 四点共圆,
∴∠BMD=∠BAD=45°。
我们发现,∠BMD所在的多边形中,很难寻找出与它有关的角度关系。通过观察图形,容易证得线段AB的同侧有两个直角∠AMF和∠ADB,通过取斜边AB的中点O,根据“直角三角形斜边上的中线等于斜边的一半”,得到A、B、D、M到斜边中点O的距离相等,根据“到定点的距离等于定长的点都在同一个圆上”,巧妙地在多边形中构建出了圆的模型,结合圆的相关性质,使得思路立刻开阔明朗起来。

图(3)
例2.(2017年广东省中考卷第25题改编)如图(3),在平面直角坐标系中,O为原点,四边形ABCO是矩形,点A、C的坐标分别是(0,2)和,点 D 是对角线AC上一动点(不与A、C重合),连结BD,作 DE⊥DB,交 x轴于点E,以线段DE、DB为邻边作矩形BDEF。求证
常规方法:
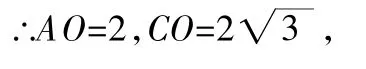
如图(4)所示,过点D作DG⊥OC于点G,DH⊥BC于点H,

图(4)

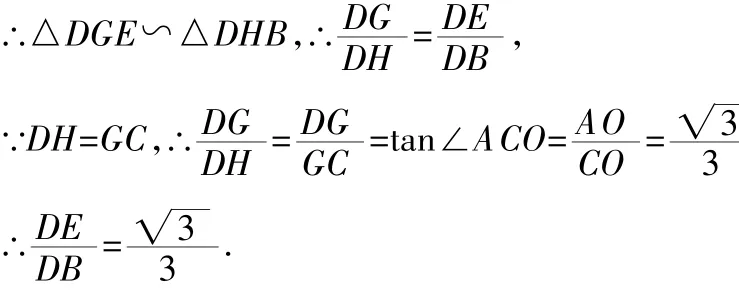
该方法采用了相似三角形的判定和性质、矩形的性质、锐角三角函数的相关知识,综合性较强,有一定的难度,解题的关键是作辅助线,构造相似三角形。
下面赏析四点共圆的证法:
证明:如图(5),连接BE,取BE的中点K,连接DK、KC.

图(5)
∵四边形ABCO与四边形BDEF是矩形,

在2017年广东省中考数学卷的最后一题中,两个矩形交叠在平面直角坐标系中出现了多个直角,本文对这道压轴题进行了适当改编,采用常规方法和四点共圆法进行对比证明,可以看出四点共圆证法所具有的明显优势。此题实际上是两个直角在公共斜边异侧的情况,通过对比例1、例2可以发现,共斜边的两个直角三角形顶点共圆是常见的四点共圆模型。
二、探究四点共圆
在人教版数学教材九年级上册第二十四章《圆》章末的“数学活动2”中,教材颇有用意地安排了“探究四点共圆的条件”这一探究活动,其探究结论即为四点共圆常用的另一判定方法:如果四边形的一组对角互补,那么这个四边形是圆内接四边形,也就是四边形的四个顶点共圆。下面对该判定方法进行证明:
已知:四边形ABCD中,∠A+∠C=180°
求证:A,B,C,D 四点共圆。
证明:过 A,B,D 作圆 O,
假设C不在圆O上,点C在圆外或圆内,如图(6),
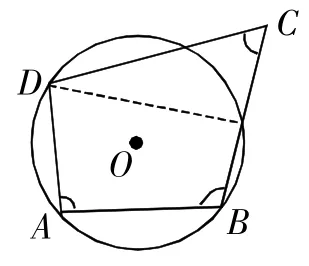
图(6)
若点C在圆外,
设BC交圆O于C′,连结DC′,
根据圆内接四边形的性质得∠A+∠DC′B=180°,
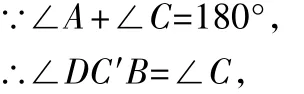
这与三角形外角定理矛盾,
故C不可能在圆外。
类似地,如图(7),可证C不可能在圆内
∴C在圆O上,也即A,B,C,D四点共圆

图(7)
例3.如图,矩形ABCD中,连接AC、BD相交于点O,延长CB到E,使CE=AC,连接 AE,F 是 AE 中点,连接 DF,与AB相交于点G,连接BF。
求证:BF⊥DF。
常规方法:
证明:如图(8),延长 BF,交 DA的延长线于点M,

图(8)
∵四边形ABCD是矩形,

本题考查了矩形对边平行且相等、对角线相等的性质、全等三角形的判定和对应边相等的性质,等腰三角形三线合一的性质,其中求证DB=DM是解题的关键。
下面赏析四点共圆的证法:
第1步:如图(9),连接 CF,在等腰△ACE中,用三线合一性质得CF⊥AE,即∠CFA=90°;

图(9)
第2步:可证∠CFA+∠ADC=180°,得点A,F,C,D共圆,即F在△ACD的外接圆上;
第3步:可证∠ABC+∠ADC=180°,得点 A,B,C,D 共圆,即B在△ACD的外接圆上;
第4步:可得F,B,C,D共圆,由圆内接四边形对角互补的性质可证∠BFD+∠BCD=180°,可得∠BFD=90°,即 BF⊥DF。
此证法在已知条件和结论中都没有出现圆弧的情况下,根据“如果四边形的一组对角互补,那么这个四边形就是圆的内接四边形,也就是四边形的四个顶点共圆”这一判定方法得出四点共圆,起了关键作用。
虽然四点共圆问题在中考中直接考查的意图不明显,在一些颇有难度的试题中,用我们常规使用的基本图形、基本技能和基本思想也能解决,但较为繁琐。而构造四点共圆,通过引入圆的模型,仿佛帮我们打开了另一扇窗户,使人豁然开朗。可以认为,四点共圆问题是圆弧线形式的辅助线,其作为研究方法的多样性和灵活性,对于培养学生的思维水平与提高推理能力有着非常重要的作用。
