改进的形态学干涉图滤波方法

张 斌, 胡庆荣, 韦立登, 李 爽

(1. 北京无线电测量研究所, 北京 100854; 2. 中国航天科工集团第二研究院, 北京 100854)

0 引 言

干涉合成孔径雷达(interferometric synthetic aperture radar, InSAR)通过利用两幅或多幅SAR图像的相位信息可以获取大范围、高精度的地表三维信息[1-2]。其利用相位信息反演高程信息,但其干涉相位图仍然存在较为严重的噪声(雷达系统的热噪声、SAR处理过程中的相干斑、干涉基线引起的相位噪声、雷达阴影、配准误差等),而噪声(尤其斑点噪声)的存在使得干涉相位图出现很多孤立的残差点,同时相位的连续性和一致性受到影响,给后续相位解缠造成困难,也影响InSAR的测高精度[3-5]。因此在InSAR处理过程中,有必要对干涉相位图进行滤波操作,最大限度消除残差点对相位的影响,提高信噪比和相位解缠的精度及效率。

目前,干涉图滤波方法主要包括空间域滤波、频率域滤波、时频域滤波和几何学滤波等4大类。圆周期均值或中值滤波[6]作为典型的空间域滤波方法,其算法较为简单,运算速度快,但其在条纹密集区域和条纹稀疏区域时效果差别较大,条纹密集区域容易出现细节丢失现象。继而出现的鲁棒加权圆周滤波[7]结合干涉图中条纹的特点,使滤波效果得到提高,但其实现较为复杂,运算量大;而梯度自适应滤波[8]利用像素的噪声统计特性,对于干涉条纹边缘能起到较好的保护作用,但不可避免的是部分噪声区域因为梯度值大于k值(保护边缘的作用)而被保留,使得该处噪声滤波效果不佳。在频域方法中,典型的算法为Goldstein算法[9],该算法通过数据分块和频域加权进行滤波,效果优良,但其受分块大小和频域加权参数的影响较大,并且有过度滤波的倾向。时频域方法中,文献[10]提出的离散小波变换相位滤波方法能较好地保持图像的干涉条纹信息,但去噪效果不好。

而数学形态学[11]作为几何学方法具有描述图像几何形态,保持图像纹理信息的性能,故基于形态学的图像滤波算法适合于干涉相位图的滤波。形态学的滤波方法中,文献[12]针对干涉相位图的特点,提出一种修正的灰度形态学开闭操作滤波器,滤波性能优于中值滤波、模态滤波器等,但其滤波效果仍有待提高;文献[13]将干涉图进行量化处理,再运用二值形态学滤波处理,最后将量化后的滤波图进行融合得到最终的干涉滤波图,虽然该算法的处理效果一定程度上优于Candeias算法,但其量化融合的范围受到限制;文献[14]提出了基于形态学开闭重建运算的融合算法(modified version of alternate sequential filters with reconstruction, MASF),从理论和实测数据两方面进行了验证,并与局部频率估计滤波方法[15]进行对比显示出其方法的优势,但其在不同噪声环境下的稳定性和局部细节信息表现仍有待提高。基于上述分析,本文提出了一种改进的自适应梯度形态学重建算法,对梯度估计进行修正求取更优的线结构元素,并借鉴了Candeias中改进的形态学开闭运算和MASF方法的基于膨胀和腐蚀重建操作的思想进行滤波,能在去除噪声的同时有效保护相位的连续性。文章通过相位图像矢量化(正余弦化)和改进自适应结构元素使得滤波更加合理,算法的性能与两种形态学方法(Candeias方法、MASF方法)以及中值圆周滤波方法相比相位的连续性得到提升,残差点数目也更少。

1 数学形态学的相位滤波

在干涉图滤波方法中,数学形态学能够保持相位的跳变特性和相关纹理,其利用结构元素在相位图像上不断移动来确定相位之间的关系,通过其几何特征滤除叠加在相位图像上的噪声。本文算法中在数学形态学中的应用算法主要为改进的形态学开闭操作和基于膨胀和腐蚀的重建操作。

1.1 改进的形态学开闭操作

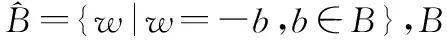
(1)

εB(φ)(x)=min{φ(y)|y∈Bx∩E}

(2)

在相位滤波中,由于相位值在[-π,π]的限制,如果直接使用膨胀和腐蚀操作进行滤波,会造成局部滤波结果不合理。而Candeias[12]对膨胀和腐蚀操作进行了修改,提出了扩大和缩小操作,使得其在进行运算时更符合真实值。扩大和缩小操作定义[12]为

(3)

min{φ(y)+L(v-φ(y))|y∈Bx∩E}

(4)

式中,+L表示模L加,此处L=2π;v表示取值范围的中心值,此处v=0。

图1(a)表示了一维相位值中的相邻三点,其相位模糊如图1(b)所示,图1(c)和图1(d)分别显示了腐蚀操作和缩小操作的结果。

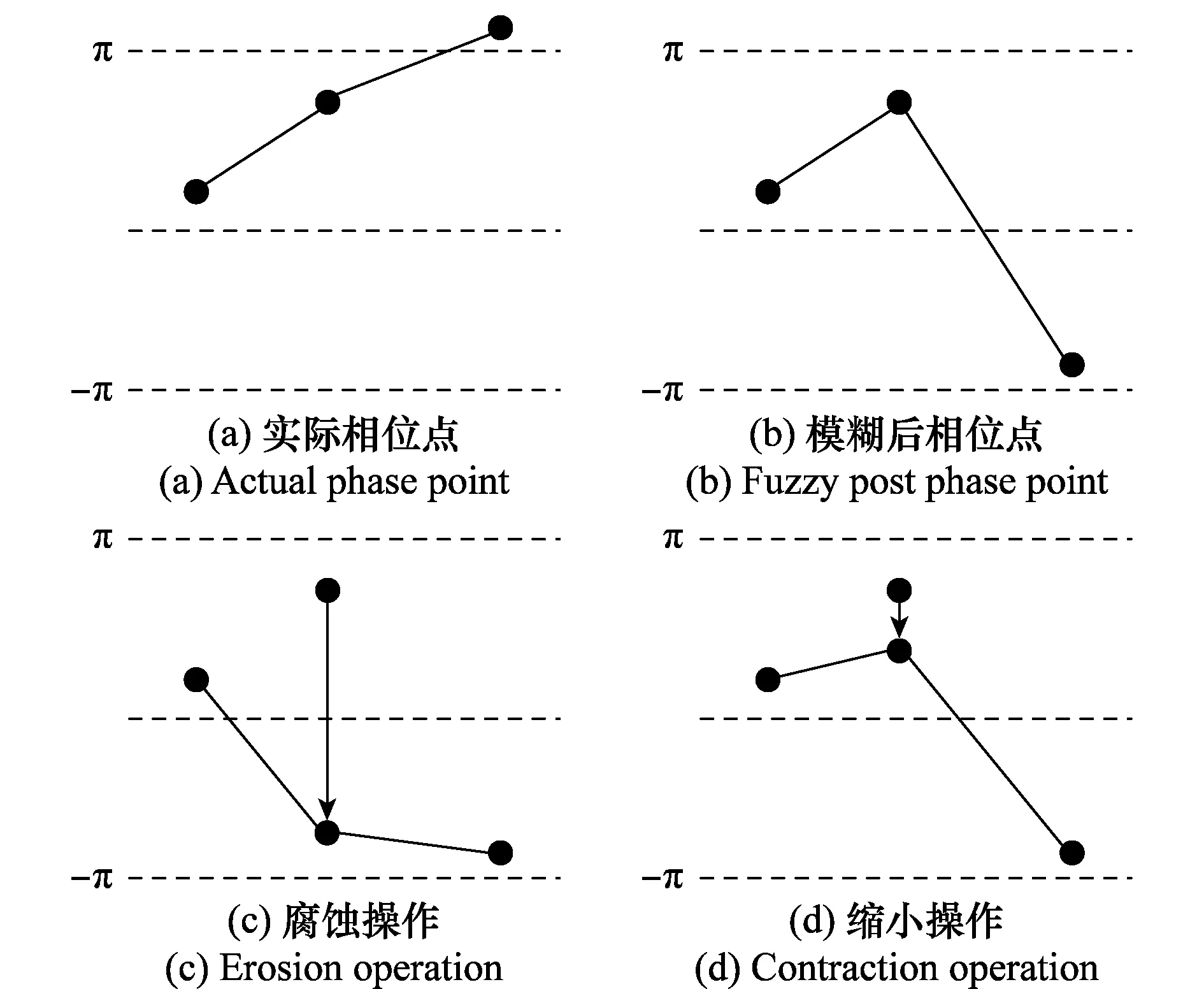
图1 腐蚀和缩小操作对比结果图Fig.1 Comparison of erosion and contraction

图1(c)和图1 (d)对比发现,3个像素中的中间像素经过缩小操作的结果比腐蚀操作更为符合实际值。

图2(a)表示了一维相位值中的相邻三点,其相位模糊如图2(b)所示,图2(c)和图2(d)分别显示了膨胀操作和扩大操作的结果。

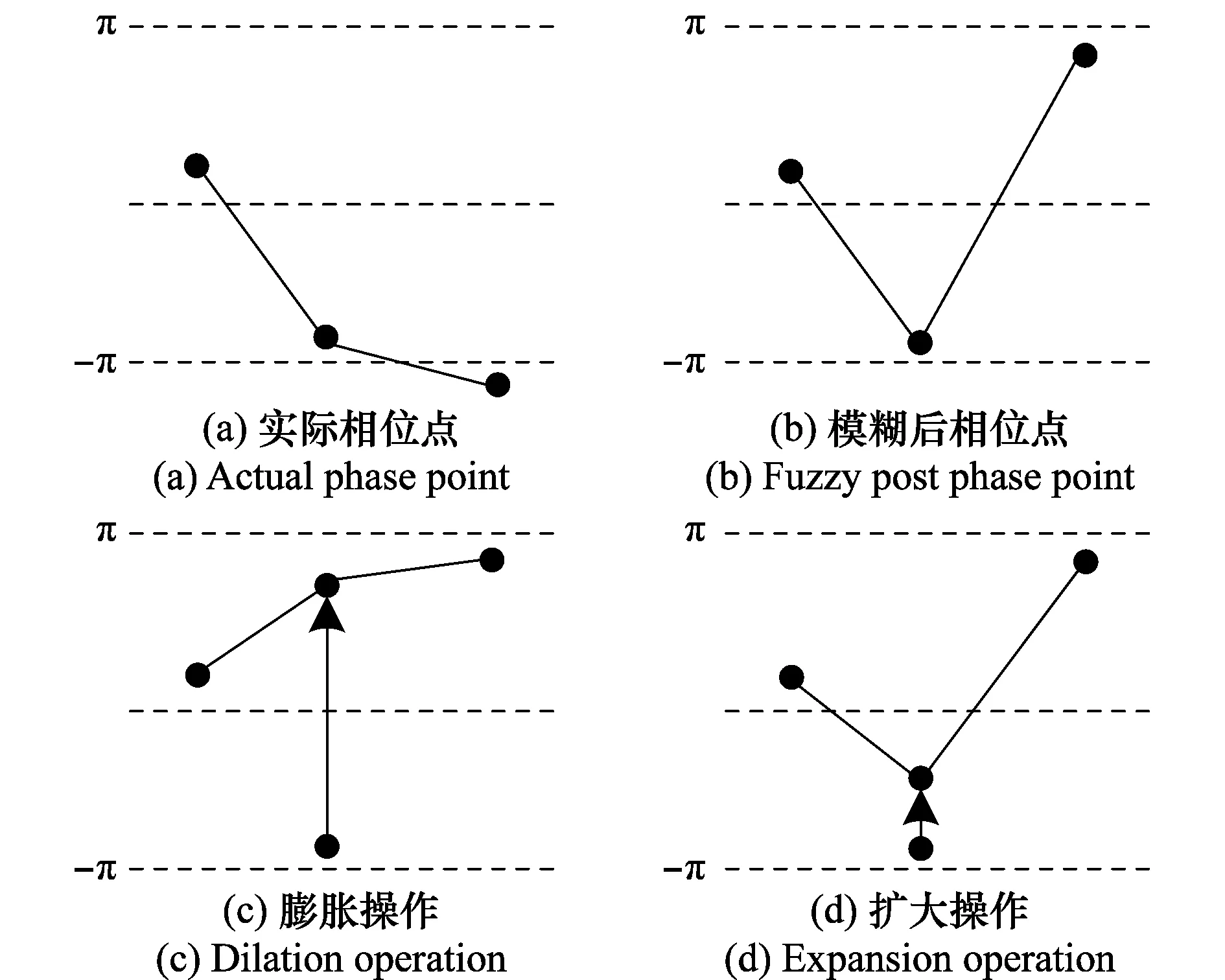
图2 膨胀和扩大操作对比结果图Fig.2 Comparison of dilation and expansion

图2(c)和图2(d)对比发现,3个像素中的中间像素经过扩大操作的结果比膨胀操作更为接近真实值。因此,改进的形态学开操作和闭操作可表示为

(5)

(6)

由于改进的形态学开操作和闭操作基于扩大和缩小操作,因此在相位滤波中进行基于改进的开闭操作滤波时,其结果比传统的形态学开闭操作更为接近真实相位值,对相位的保护更好。

1.2 基于膨胀和腐蚀的重建操作

基于膨胀和腐蚀的形态学重建运算分别可表示[16]为

(7)

(8)

(9)

(10)

式中,Rd(φ′,φ)表示基于膨胀的形态学重建操作;δB(φ′)(x)表示膨胀操作;∧表示点方式的最小算子(与相同位置处φ值的最小值);Re(φ′,φ)表示基于腐蚀的形态学重建结果;εB(φ′)(x)表示腐蚀算子;∨表示点方式的最大算子(与相同位置处φ值的最大值);φ表示模板图像,式(7)和式(9)中的k值分别表示关于φ的测地膨胀和测地腐蚀反复迭代达到稳定值时的迭代次数。

基于膨胀的重建操作是利用结构元素对φ′进行膨胀操作并将结果图像作为标记图像,然后取标记图像与原图像中每个点对应的最小值,以此进行迭代直到图像趋于稳定,该操作能够将斑点噪声有效地去除[14]。而基于腐蚀的重建操作用结构元素对φ′进行腐蚀操作并将结果图像作为标记图像,然后取标记图像与原图像每个点对应的最大值,以此进行迭代直到图像趋于稳定,该操作能够弥合一些间断的区域,保持条纹的连续性[14]。

2 改进的自适应梯度形态学重建滤波

本节对所提算法进行详尽的说明,首先是对原复数据进行矢量化,接着估计相位梯度以确定形态学操作必需的线结构元素,之后设计线结构元素进行基于改进的灰度形态学开闭运算和膨胀与腐蚀的重建滤波操作,然后进行公式反演得到滤波后的相位图。

算法的流程图如图3所示。

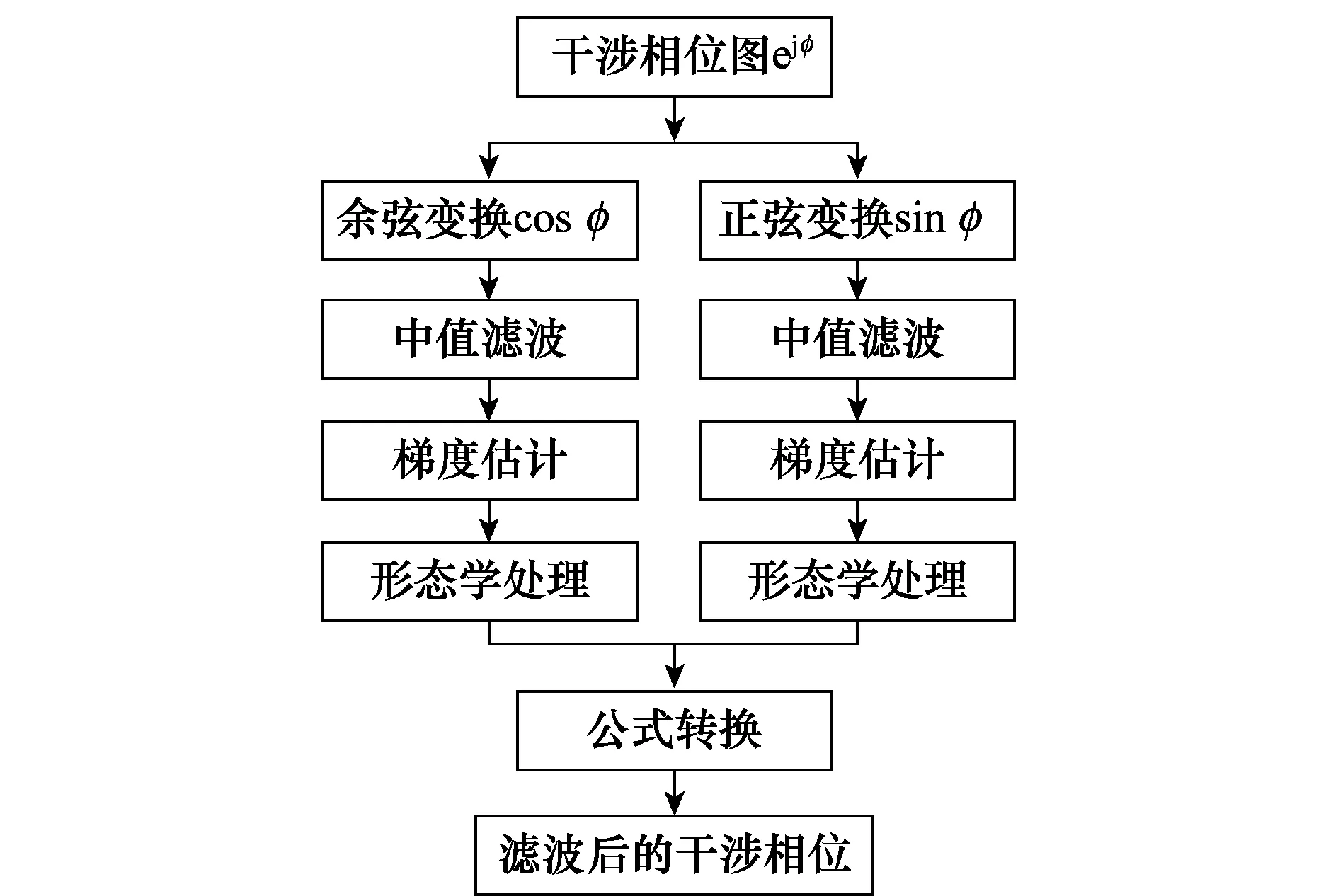
图3 算法流程图Fig.3 Flow chart of the algorithm

2.1 复数据矢量化(正余弦变换)

为了避免复数干涉图的强度信息(主辅图像强度信息)对滤波精度和效果的影响,可以把干涉图中的干涉相位进行等权处理,采用相位矢量化(正余弦化)的处理方式。而MASF方法中则对原始相位进行shifting操作(相位加π后对相位图缠绕)作为第二幅图像,两幅相位图像都存在相位的跳变,并没有对相位起到有效的保护。本文相位正余弦化的实质就是运用正余弦函数的周期性避免相位跳跃的影响,把相位图像转换为正弦图像和余弦图像,两幅相位图像不存在相位跳跃,有效保护相位条纹的连续性。后续的步骤在两幅图像(正、余弦图像)中分别进行操作。

2.2 中值滤波操作

在对相位进行正余弦化后,分离开的正余弦数据仍有很多的噪声,而本文的滤波方法中基于膨胀和腐蚀的形态学重建操作需要先确定线结构元素,而噪声的存在影响了梯度估计和线结构元素的选取,因此有必要对正余弦图像进行预滤波操作,以增强梯度估计的准确性。本文采用3×3大小的元素进行中值滤波操作,既能够对图像进行预滤波,也能有效保护相位条纹保护相位的连续性。

2.3 改进的自适应梯度估计

中值预滤波处理后,需要确定形态学处理所需的线结构元素,而线结构元素的选取由梯度估计得到。

对相位数据进行分块,在小块里面进行梯度估计,计算中心元素与窗口内各点差值的绝对值,将差值绝对值最大的点与中心点作为梯度方向,为后续线结构元素的选取提供依据。

由于在小块里面求取差值最大点,此时差值绝对值最大的点并不一定在边缘处,也可能在中间元素中(见图4)。而MASF方法中对梯度值估计时,其在小块边缘查找差值绝对值的最大值,使得所选取的差值最大点在小块的边缘上,由于相位及条纹方向的不确定性,最大值点并不能保证完全在边缘处,此时造成了梯度估计的不准确性,线结构元素为1的值也均在边缘,使得在进行形态学处理时容易造成小块内细节信息的丢失。而本方法求取的差值最大值点摆脱了该限制,差值最大点既可能在边缘上也可能在小块内,从而使得梯度估计更为准确,后续步骤线结构元素选取时不仅在边缘处有值,在小块里面也有为1的值,使得后续形态学滤波得到的细节信息更为丰富。

2.4 改进的形态学处理

2.4.1 线结构元素选取

当形态学结构元素为线结构元素时,其条纹保持能力要好于矩形平坦结构元素(矩形结构元素更平滑一些)。因此，本文在进行形态学处理时选取线结构元素作为结构元。文中选取垂直于梯度方向的元素点位置(不止有边缘点)作为线结构元素(值为1)。由于梯度估计时最大值点不一定在边缘处,使得小块内部也存在线结构元素的点(见图4中线结构元素L1在小块内部有两个点作为线结构元素的一部分),从而形态学滤波更为合理,有效保护相位条纹的细节信息。此外为了系统的鲁棒性考虑(尽量避免噪声的影响),将与线结构元素距离最近的两条线结构元素也作为后续的处理。如图4所示,本小块内的线结构元素为L1、L2、L3。

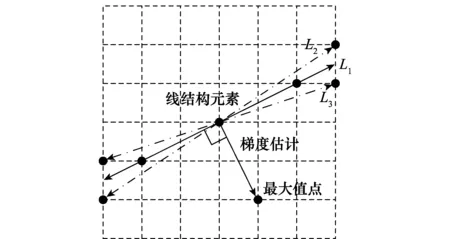
图4 梯度估计Fig.4 Estimation of gradients

2.4.2 改进的形态学灰度开闭操作和重建操作的滤波

线结构元素选取之后,进入改进的基于灰度形态学开闭运算和膨胀及腐蚀的重建操作。改进的形态学开操作能够平滑相位图像的轮廓,并能消除细小的孤立区域和孤立噪声像素;改进的闭操作能够弥合细小的空洞,填补条纹线的断裂[16];基于膨胀的重建操作能够将斑点噪声有效去除;而基于腐蚀的重建操作能够弥合一些间断的区域,保持细节的连续性[14]。

首先利用3个线结构元素(L1、L2、L3)依次对图像中选取的小块进行改进的形态学开运算,选取3个小块中对应像素的最大值,将其作为标记图像,并将该步骤前的相位图作为模板图像,进行基于膨胀的形态学重建操作。该步骤可用公式表示为

(11)

式中,φ1为正余弦化和中值滤波后的相位图;χi(·)表示用线结构元素L1、L2、L3分别进行改进的形态学开操作运算，i=1,2,3;Rd表示基于膨胀的重建操作。

其次分别利用3个线结构元素(L1、L2、L3)对形态学膨胀重建操作后的图像进行改进的形态学闭运算操作,选取3个小块中对应像素的最小值,将其作为标记图像,并将该步骤前的相位图作为模板图像,进行基于腐蚀的形态学重建操作。该步骤可用公式表示为

(12)

式中,γi表示用线结构元素L1、L2、L3分别进行改进的形态学闭操作运算(i=1,2,3);Re表示基于腐蚀的重建操作。

式(11)和式(12)类似于基于开(闭)操作的形态学重建(先腐蚀(膨胀)输入图像,后进行基于膨胀(腐蚀))的重建)[16],其有效地保留了相位图像腐蚀(膨胀)后留下的相位分量的形状,减弱噪声的影响,同时其利用改进的形态学开(闭)运算和3个线结构元素的优化处理提高了相位滤波的鲁棒性。

通过式(11)和式(12)的基于膨胀和腐蚀的形态学重建滤波操作,得到正余弦化后的相位滤波图φsin和余弦化后的相位滤波图φcos。

2.5 公式转换

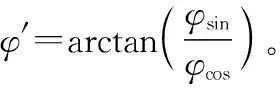
(13)

3 试验结果分析

本文同时进行仿真和实测数据处理试验,并与中值圆周滤波[6]、Candeias方法[12]、MASF方法[14]方法进行对比验证所提方法的滤波效果。

3.1 仿真分析

文章将Matlab生成的peaks面作为相位仿真曲面来验证所提算法的滤波效果。相位缠绕后的图像如图5(a)所示,数据大小为512像素×512像素。图5(b)为带噪声的缠绕相位图,图中所加噪声为1视相干系数为0.9、标准差为0.422 5的均匀噪声[17]。上述4种方法分别对该干涉图进行滤波处理,相应的滤波结果图如图5(c)～图5(f)所示,统计信息(残差点数目[18]和滤波前后的均方根误差(root mean square error, RMSE))如表1所示。

表1 算法仿真实验比较

从图5可以看出MASF方法滤除效果较差,对噪声的滤除较差,且对条纹造成了一定程度的破坏。中值圆周滤波和Candeias方法能滤除一部分噪声,但仍有噪声未能去除。而本文方法能有效滤除噪声,且条纹保持性能较好。

为了定量分析上述方法的仿真滤波效果,现采用滤波前后的RMSE和残差点数目[18]作为判断依据,各方法的统计结果如表1所示。

从表1可以看出本文方法滤波后的残差点数目较少,与原始相位图的均方根误差也较少。

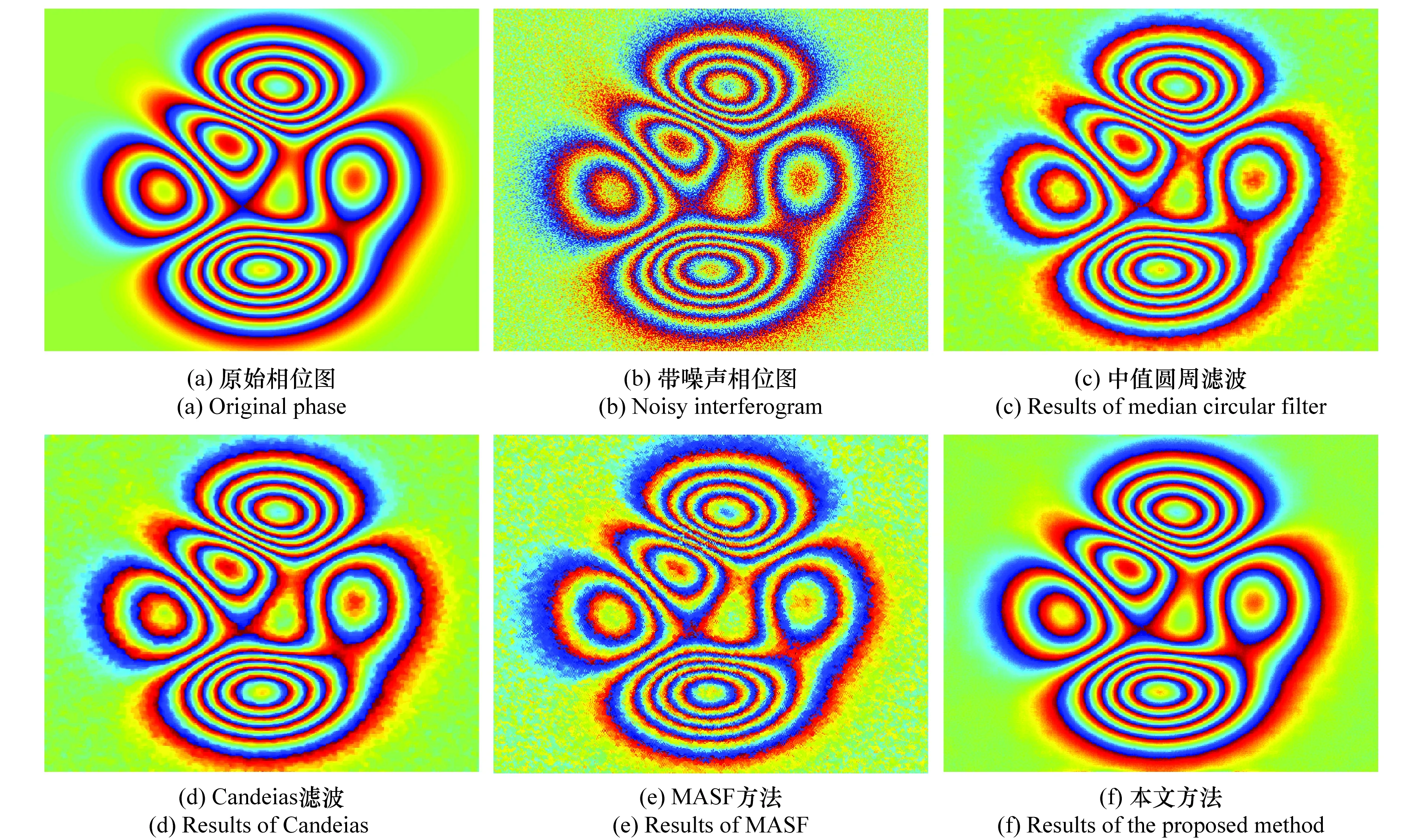
图5 仿真实验结果图Fig.5 Results of simulation with different methods

仿真分析可以看出,本文方法的噪声滤除效果较好,且条纹保持能力强于上述比较的方法。

3.2 实测数据处理及比较

为了验证其在实测数据中的滤波效果,为此选取毫米波InSAR的数据进行处理,并与其他方法进行比较。图6(a)所示为机载毫米波InSAR系统获取的中国西南某地区的干涉条纹图,大小为4 096像素×4 096像素。其相应的相干系数图如图6(b)所示,图6(b)右侧坐标代表相干系数的大小。从相干系数图(计算窗口33×33)可以看出该相位数据有较多的低相干区域,对干涉处理造成较大的影响。4种方法的滤波结果如图6(c)～图6(f)所示。

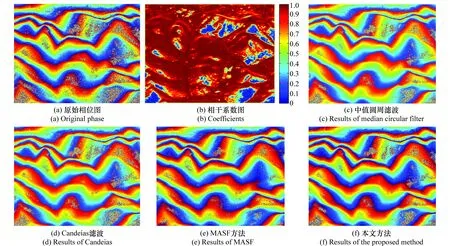
图6 实测实验结果图Fig.6 Results of filtering in real data

从图6可以看出中值圆周滤波和Candeias方法对高相干区域有过度滤波的倾向,使得条纹相对变暗,条纹保持性能相对较差。而MASF方法对低相干区域的滤除效果相对不足,与本文方法相比,有更多的低相干区域并未滤除。而本文方法的噪声滤除效果较好,既能在高相干区域保持较好的条纹,也能最大限度地滤除低相干区域的噪声。但由于部分噪声是阴影造成,为无效区域,无法进行滤除,因此各方法均在一定区域都无法对噪声进行滤除。

为了定量分析上述方法的滤波效果,现采用残差点数目[18]、滤波后平均伪相干值[19]来评价滤波效果,相关统计结果如表2所示。

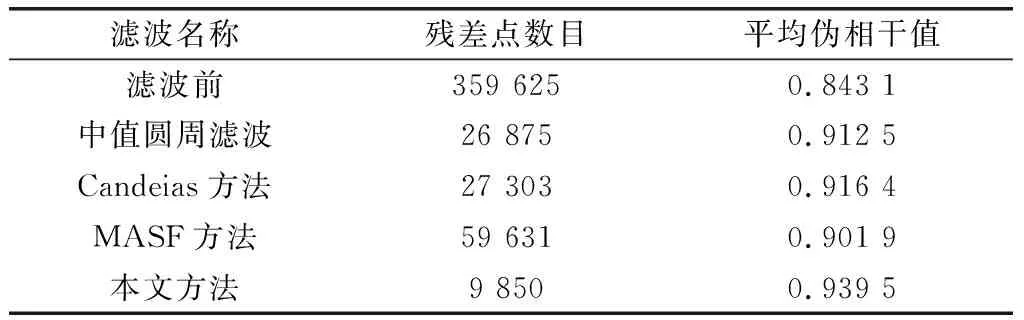
表2 相关评价指标对比结果

从表2中也可看出,MASF方法的平均伪相干系数最小,残差点数目也最多,滤波并不充分;中值圆周滤波、Candeias滤波方法较为适中,其伪相干系数较高,残差点数目也较少,而本文方法的滤除效果相对最好,其平均为相干系数最高,残差点也最少,可以看出表中统计结果与图6实测实验结果图相一致。

为了进一步验证其该方法在去噪及相位条纹保持方面的性能,选取第二组实测数据进行实验,并与其他方法进行比较。图7(a)所示为机载毫米波InSAR系统获取的中国东南某地区的干涉条纹图,大小为512像素×512像素,由于该系统基线较长,故条纹比较密集。其相应的相干系数图如图7(b)所示,图7(b)右侧坐标代表相干系数的大小。从相干系数图(计算窗口9×9)可以看出该相位数据左侧区域有较多的低相干区域,对干涉处理造成较大的影响。4种方法的滤波结果如图7(c)～ 图7(f)所示。

从图7(e)可以看出MASF方法左侧区域仍有部分噪声尚未滤除,右侧区域滤波效果较好。图7(c)和图7(d)中的两种方法中值圆周滤波和Candeias方法在高相干区域滤波效果略好于MASF方法,而在低相干区域的滤波较差,使得不连续区域较多,条纹保持性能相对较差。而本文方法不仅在右侧相干系数较好的区域噪声滤除效果较好,条纹更为明亮清晰,在左侧区域也能较好地实现滤波,同时细节信息也比较丰富,相位条纹保持较为良好。

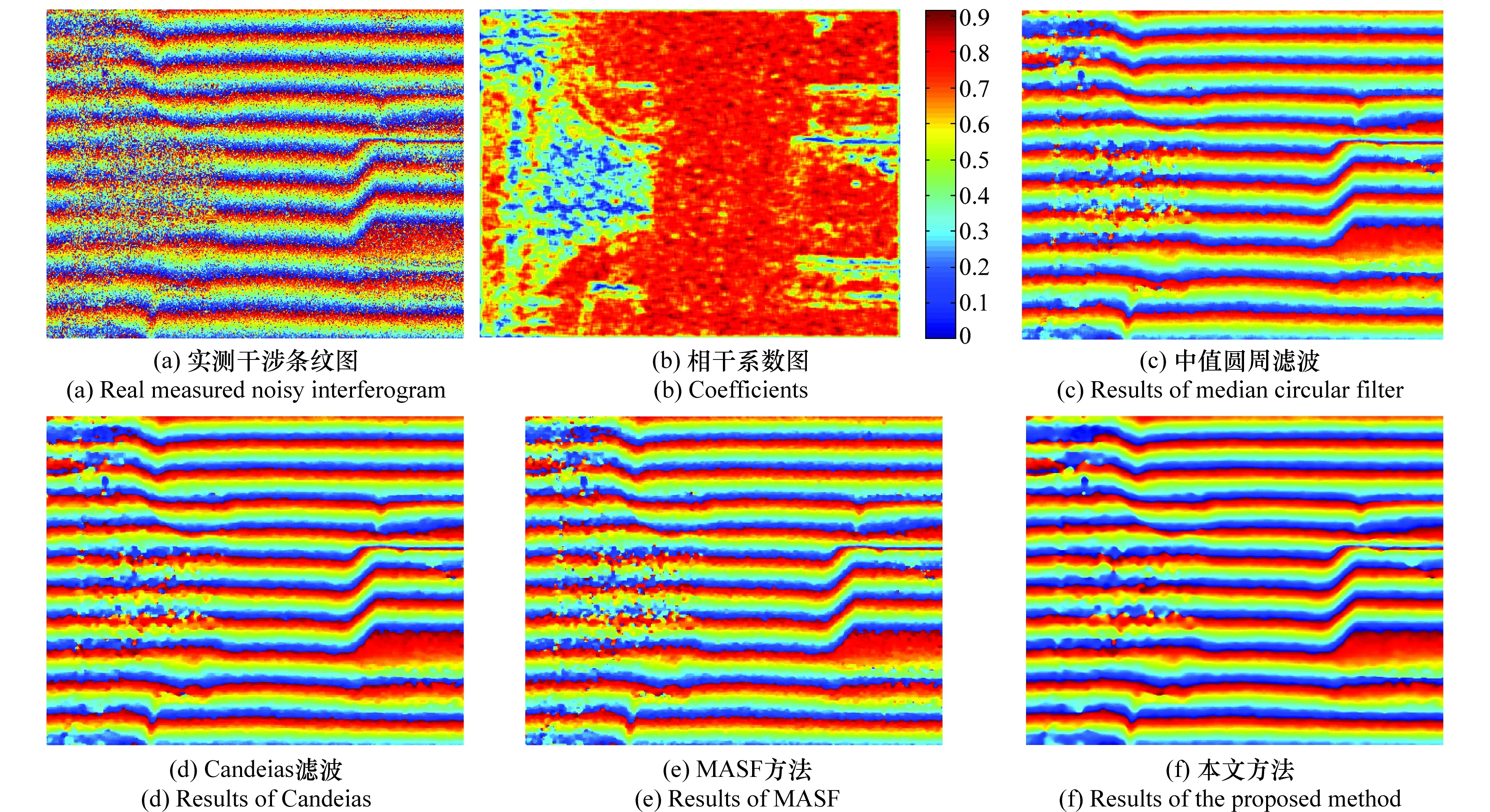
图7 实测实验结果图Fig.7 Filtering results in real data

为了定量分析上述方法的滤波效果,采用残差点数目[18]、滤波后平均伪相干值[19]来进行评价滤波效果,相关统计结果如表3所示。

从表3中也可看出,4种方法的平均伪相干值和残差点数目预滤波前相比有明显改善。其中,MASF方法的平均伪相干系数最小,残差点数目也最多,滤波并不充分;中值圆周滤波、Candeias滤波方法较为适中,其伪相干系数较高,残差点数目也较少,而本文方法的滤除效果相对最好,其平均伪相干系数最高,残差点也最少,可以看出表中统计结果与图7实测实验结果图相一致。

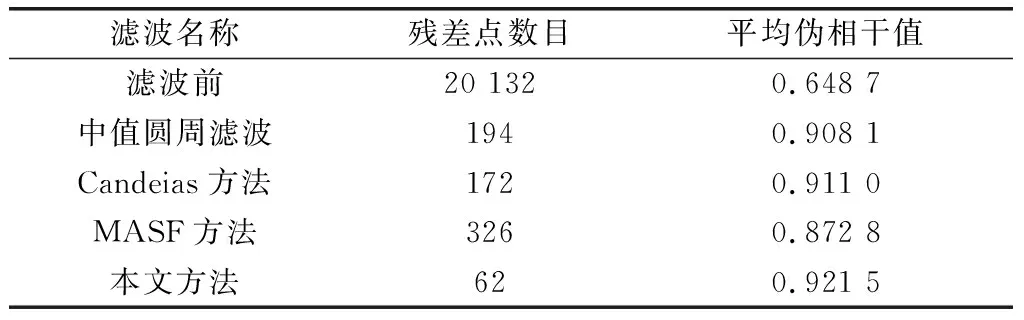
表3 相关评价指标对比结果

两组实测数据实验分析可以看出,本文方法不仅能较好地滤除噪声,且能有较好的条纹细节保持能力。

4 结 论

文中提出了一种改进的自适应梯度形态学重建滤波算法。算法基于改进的灰度形态学开闭运算和基于膨胀与腐蚀重建滤波操作,利用复数据的矢量化和改进的梯度估计有效地保护相位的跳跃特性及连续性,改进的自适应的线结构元素使得细节信息不被破坏。仿真分析和实测数据对比处理表明该方法的滤波效果较好,细节表现力也较强。