基于多特征的密集假目标干扰融合识别与抑制
2018-10-15孙殿星万建伟王国宏
孙殿星, 陈 翔, 万建伟, 王国宏, 吴 巍
(1. 电子信息系统复杂电磁环境效应国家重点实验室, 河南 洛阳 471003;2. 国防科技大学电子科学学院, 湖南 长沙 410073;3. 海军航空大学信息融合研究所, 山东 烟台 264001)
0 引 言
密集假目标干扰是一种基于数字射频存储(digital radio frequency memory, DRFM)技术的新型干扰样式[1-2],干扰机通过截获、复制、调制和转发雷达信号,产生大量欺骗干扰回波,由于干扰信号与雷达回波信号具有高度的相干性,因此大量的虚假回波能够获得雷达接收机的处理增益,并顺利通过门限检测,最终在雷达中形成密集的虚假目标。该型干扰兼具了欺骗式和压制式干扰的特点,不但能够形成虚假的空情态势,而且会影响到真实目标的检测、跟踪。目前,针对密集假目标干扰的研究更侧重于干扰的产生与干扰效果的评估等[3-11],对于如何对抗密集假目标干扰的研究相对要少,其中:文献[12]采用盲源分离的方法从密集假目标干扰中检测出目标回波信号,为雷达抗密集假目标干扰提供了新思路,但该方法是以阵列天线雷达为应用背景,对普通体制雷达并不适用,并且对于完全转发式密集假目标干扰已经很难在时-频域对目标和干扰进行有效的分离[13];文献[14]提出了基于主被动雷达组网的抗密集假目标干扰技术,但是该方法仅能对干扰机进行定位和跟踪,不能抑制单部雷达中的虚假回波,因此对检测干扰掩护下的其他目标并没有显著帮助;文献[15] 提出了一种“二次判决”的方法,能够有效改善旁瓣匿影对密集假目标干扰的抑制效果,但对于从主瓣进入的虚假回波,其抑制作用仍然有限;文献[16]利用正交基对雷达发射脉冲做特殊调制,以达到干扰抑制的目的,但同时也限制了该方法的普适性;文献[17]则通过理论分析和仿真试验的手段,分析了动目标显示(moving target indicator, MTI)技术对密集假目标干扰的抑制能力,但对于具有多普勒调制的密集假目标干扰MTI往往抑制作用有限。
针对上述问题,本文以单部脉冲多普勒雷达受到具有多普勒调制信息的密集假目标干扰为背景,在综合分析密集假目标干扰数据层和信号层特点的基础上,首先提出了基于速度量测统计分布特性的干扰判别方法,以实现干扰态势的准确判定,然后通过多普勒频率估计和峰值邻域谱线抑制,在频域实现部分干扰信号的剔除,最后通过谱线分布和信号幅度基本概率赋值构建,及D -S证据理论融合判别,进一步识别和抑制干扰信号。
1 密集假目标干扰特征分析
密集假目标干扰与其他类型的欺骗干扰(如:航迹欺骗、距离欺骗)有所不同,其与真实目标信号保持高度相关以获得雷达的处理增益,同时更侧重以绝对数量优势压制雷达对真实目标的检测、识别,扰乱目标跟踪系统,而其他类型的欺骗干扰则侧重于虚假目标回波的逼真性,以航迹欺骗干扰为例,其虚假回波信号的多普勒调制信息要与航迹运动状态精确匹配,目标雷达截面积(radar cross section, RCS)要有实时的随机起伏,这些参数均需要进行实时解算和精细调制[18-20],必定会消耗干扰机大量资源,导致产生的虚假航迹数量往往受限。对于密集假目标干扰,需要在相参处理周期(coherent processing interval, CPI)内复制和转发大量虚假信号,若对每个虚假信号均进行精细的幅度和多普勒调制,必定会大大增加干扰机负担,在计算资源和调制能力有限的条件下,这个目标往往是无法实现的[21],因此干扰机在信号幅度、多普勒调制的精细化处理上会做出相应让步,例如:DRFM干扰机在每个CPI内幅度调制能力有限,可以认为脉冲幅度是恒定的[21];对于不具有多普勒处理能力的雷达,干扰机可能不具有多普勒调制的功能;对于具有动目标显示、动目标检测(moving target detection, MTD)功能的雷达,干扰机通常选择一个固定多普勒频率或从多个固定的多普勒频率中随机选择某一个频率对虚假目标回波进行多普勒调制,这样不但可以获得多普勒处理增益,而且可以大大减轻干扰机信号处理负担。
综合上述分析,我们可以初步得到密集假目标干扰在某个CPI内的特征:大量虚假点迹的径向速度量测集中分布在若干个数值的有限邻域内;不考虑噪声影响的情况下,信号幅度为某一固定数值,但由于噪声的存在,其幅度服从莱斯(Rician)分布概率密度函数如下[22]:
(1)
式中,f(A)为概率密度函数;A为信号加高斯分布随机噪声的包络;σ为随机噪声方差,对应于噪声功率;β对应于信号幅度;I0(·)是修正的第一类贝塞尔函数。
虽然在CPI内存在大量虚假目标给雷达带来了很大麻烦,但同时也为干扰识别提供了充足的样本,这也是可以为我们所利用的一点。
2 干扰态势判别
对密集假目标干扰态势进行正确判别是对抗和抑制干扰的前提,根据前文干扰特征分析,当雷达受到密集假目标干扰时在数据层会出现两个明显特征:雷达中的点迹数量突然大幅增加,点迹径向速度量测集中在若干个数值附近。基于上述特点本文提出基于速度量测统计分布特性的干扰判别方法。设在当前CPI内经雷达接收机处理得到的点迹(包括真实目标点迹和虚假点迹)数目为N1,在前一个CPI内的点迹数目为N0,若满足式(2)则可以初步推断:可能存在密集假目标干扰。
(2)
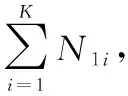
(3)
式中,RG为判别门限,反映了落在集合Ψ1i中的速度量测占量测总数的比例,由于密集假目标点迹数量通常远远超过真实目标,所以RG通常选取与1很接近的数值,在本文中取RG=0.975,该门限对应具有某些特定速度的点迹数占所有点迹数的比例,因此其取值并不是根据某种统计特性而定,而是根据密集假目标干扰强度和通常真实目标点迹的数量等经验而选取。若经过判别确定存在密集假目标干扰,则可以利用Ψ1i中的样本对虚假目标的径向速度和量测误差方差进行估计:
(4)
(5)
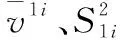
3 密集假目标干扰抑制
3.1 基于多普勒频率估计的干扰初步抑制
(6)
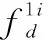
(7)
式中,fr为雷达的脉冲重复频率。
为了下一步构建基于信号幅度特征的基本概率赋值,需要记录干扰信号的幅度作为统计样本,因此在峰值搜索并确定峰值位置后,需利用获得的频率和幅度信息,通过二次多项式内插估计信号幅度,设得到的幅度估计为Ai,具体计算过程本文不再赘述。
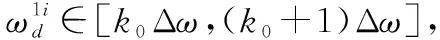
设在DFT峰值附近第k个频点ωk与对应的DFT采样|Sk|满足二项式:
式中,a0、a1、a2为未知系数,将3组样本点[(k0-1)Δω,|Sk0-1|]、[k0Δω,|Sk0|]、[(k0+1)Δω,|Sk0+1|]代入上式,得到二项式系数,从而确定了|Sk|的函数形式,其中|Sk0-1|、|Sk0|、|Sk0+1|分别为第k0-1、k0、k0+1个频率采样处的信号幅度,通过微分该多项式并令其结果为零,可求得内插峰值频率,令Δωk为内插峰值的频率与搜索峰值频率的差值[23],则有
(8)
并且有约束条件:
(9)
式(8)可进一步整理为
(10)
若以|Sk0-1|为自变量,可知:无论|Sk0|、|Sk0+1|的取值如何,在式(9)的约束下当|Sk0-1|=|Sk0|时Δωk取极小值-Δω/2。同理:当|Sk0+1|=|Sk0|时,Δωk取极大值Δω/2,所以当k0为峰值时,抑制范围是[(k0-1/2)Δω,(k0+1/2)Δω]。
同样,当搜索得到的峰值位置为k0+1时,抑制的频率范围是[(k0+1/2)Δω,(k0+3/2)Δω],综合峰值位置在k0、k0+1两种情况,可知:本文的峰值邻域谱线抑制方法能够在[(k0-1/2)Δω,(k0+3/2)Δω]频域范围内抑制密集假目标干扰。
3.2 基于谱线分布特征的基本概率赋值构建
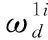
(11)
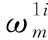
(12)
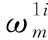
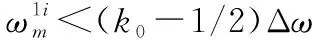
(13)
(14)
其中PL表示推断总体的不确定性:
(15)
其取值通常依据具体工程背景而定,由于本文是以对空警戒雷达为背景,且主要针对距离较远的情况,因此受杂波等不确定因素影响较小,则设定PL=0.05,Φ(·)是正态分布积累分布函数:
(16)
Φ(Gα)=α
(17)
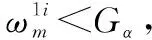
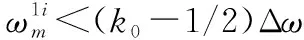
(18)
(19)
3.3 基于信号幅度统计特征的干扰识别与基本概率赋值构建
根据前文分析可知:在同一个CPI内,密集假目标干扰的信号幅度近似服从莱斯分布,其概率密度函数如式(1)所示,而对于实际的航空目标其RCS通常是起伏的,导致其信号幅度会有相对较大的波动,与密集假目标干扰信号幅度的统计特征有较大区别,针对这一差别,本文借鉴假设检验的思想对干扰信号进行识别,并构建其基本概率赋值函数。
设在第3.1节的干扰抑制过程中,记录的信号幅度样本为Ai(i=1,2,…,M),将式(1)中的Bessel函数渐进展开[25]为
(20)
取一阶近似可得莱斯分布的近似表达式:
(21)
从而可得参数σ2、β的最大似然比估计:
(22)
(23)
其中
(24)
(25)
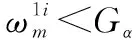
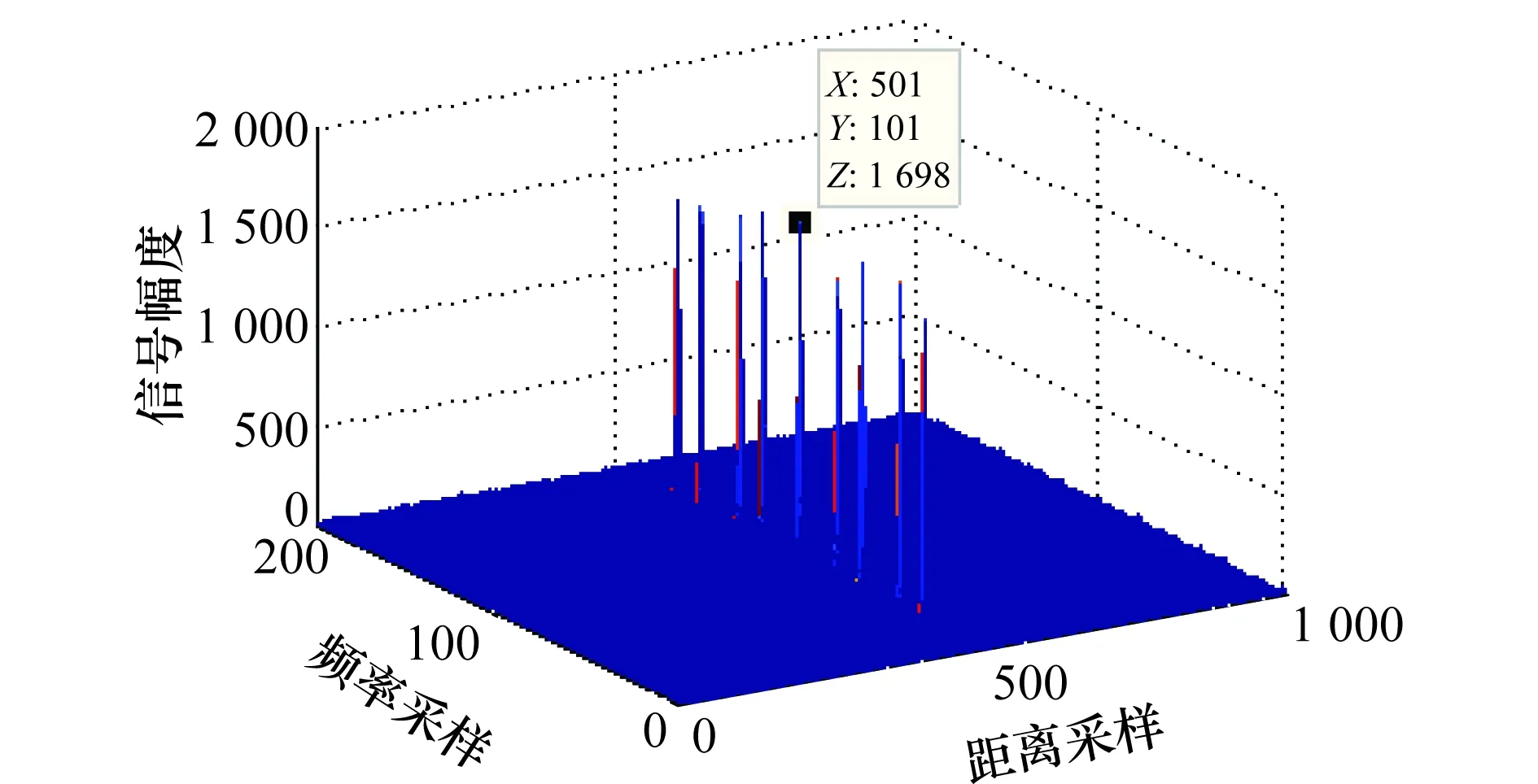
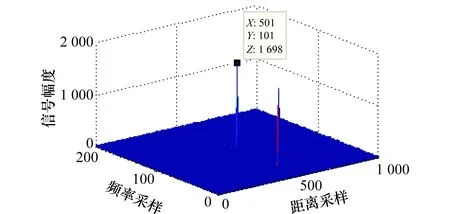
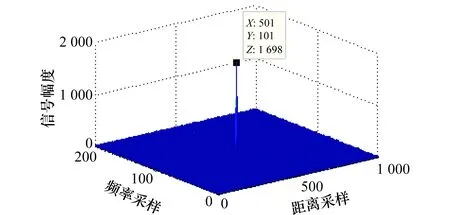
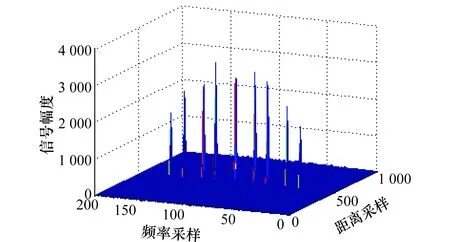
设莱斯分布概率密度函数峰值对应的随机变量为Prician,可知:相对其他的区间而言,在Prician的邻域内能够以较小的区间长度占据较大的积累概率。因此,可在Prician的左右两侧取4个门限G1 Ω(G3)-Ω(Prician)=Ω(Prician)-Ω(G2)=η1 (26) Ω(G4)-Ω(Prician)=Ω(Prician)-Ω(G1)=η2 (27) 式中,0<η1<η2;Ω(·)是莱斯分布的积累分布函数;具体参数由式(22)、式(23)确定。 经过第3.1节的干扰初步抑制后,一定会有部分干扰信号剩余,因此需要进一步识别,设其中某一峰值幅度为Ap,首先利用门限Gi(i=1,2,3,4)进行判别,判别准则如为:Ap>G2且Ap 下面求解判别门限Gi(i=1,2,3,4),首先计算峰值随机变量Prician,然后根据设定的概率η1、η2计算Gi。对式(21)给出的莱斯分布近似式求导 (28) 对A>0的情况,求解方程 (29) 化简为 2A2-2βA-σ2=0 (30) 求解方程,用参数估计代替各参数,并取其中的正数解,可得 (31) 为了方便计算机处理,需利用莱斯分布与非中心卡方分布的定量关系[26],借助非中心卡方分布的分位数表等工具,求解莱斯分布的分位数,由式(26)有 Ω(G3)=Ω(Prician)+η1 (32) 设φκ(·)为非中心卡方分布的积累分布函数,κ为非中心参量,由两种分布的关系可推得 (33) (34) 则 (35) (36) (37) (38) 当G3 (39) (40) D -S证据理论是由Dempster和Shafer建立的一套数学理论,适用于专家系统和模式识别等[27-28],本文采用依据准贝叶斯结构的证据理论进行基本概率赋值合成[29],设合成后干扰和目标的基本概率赋值分别为m(FT)、m(T),则有 (41) (42) (43) (44) 结合本文的工程背景,可构建融合识别准则如下: 判定为干扰信号 (45) (46) 同时,根据识别结果,抑制判定为虚假目标的干扰信号。 密集假目标干扰融合识别与抑制算法流程如图1所示,虽然具体的算法步骤较多,但总体可分为3个部分:干扰态势判别、多普勒峰值邻域干扰初步抑制、基于D -S证据理论的干扰融合判别与抑制。 具体算法步骤如下: 步骤1基于数据层点迹数量和径向速度信息,判别干扰态势。 由于较短时间内假目标的多普勒调制相对稳定,因此可以利用之前的径向速度估计确定干扰信号在频域内所处的DFT单元,然后判别该DFT单元端点是否为局部峰值,并采用邻域谱线抑制的方法对干扰进行初步抑制。当然随着时间的推移,之间对多普勒频率的估计与实际量测之间会产生偏差,此时需要重复前面的步骤,对多普勒频率进行估计。 图1 密集假目标干扰融合识别与抑制算法流程图Fig.1 Block diagram of fusion identification and suppression algorithm of concentrated false targets jamming 步骤4基于统计判别的真实目标识别。 步骤5基于谱线分布特征的基本概率赋值构建。 步骤6基于信号幅度统计特征的干扰识别与基本概率赋值构建。 步骤7基于D -S证据理论的干扰融合判别与抑制。 基于步骤5和步骤6构建的基本概率赋值函数,采用D -S证据理论的方法进行基本概率赋值合成,根据合成基本概率赋值采用式(45)和式(46)对密集假目标信号进行识别,并进行干扰抑制。 仿真条件:雷达脉冲重频600 Hz、工作频率3 GHz、脉宽500 μs,采用线性调频信号;真实目标数量为1,与真实目标在同一距离分辨单元内存在8个密集假目标干扰;真目标信噪比为-5 dB,与雷达的初始距离为120 km,径向速度为15 m/s;虚假目标干噪比为-5 dB,与雷达的初始距离为120 km,径向速度分别为5 m/s、7 m/s、10 m/s、12 m/s、-5 m/s、-7 m/s、-10 m/s、-12 m/s,由信号复制、转发等环节引入的速度随机扰动标准差为0.15 m/s,蒙特卡罗仿真300次。 经脉压和相参积累后的信号如图2所示,共检测到9个峰值,其中位于中间位置的峰值(标出了位置和幅度)为真实目标,其余的为虚假目标。 图2 经脉压和相参积累后的信号Fig.2 Result of signal pulse compressionand coherent integration 经干扰初步抑制后的结果如图3所示,可见:采用的多普勒频率估计方法能够较为准确地确定虚假目标峰值所处的DFT处理单元,并且在有效抑制虚假信号的同时很好地保留了真实目标,但是仍有部分干扰信号峰值未被抑制,这是由于干扰机在调制、转发过程中会引入一定的随机误差,以及多普勒频率估计存在的偏差等因素所导致的。 图3 经干扰初步抑制的结果Fig.3 Result of elementary jamming suppression 通过引入幅度特征,对经过初步干扰抑制的信号做进一步的干扰识别和抑制,结果如图4所示。可见:通过引入幅度特征,能够有效弥补前面初步抑制所造成的遗漏。 图4 干扰融合识别与抑结果Fig.4 Result of fusion identification and suppression 其他仿真条件不变,改变密集假目标的干噪比,为了能够取得较好的干扰效果,密集假目标干扰通常具有较高的干噪比,本文使其从-7 dB逐渐增大到-2 dB,得到干扰抑制率随干噪比的变化曲线,如图5所示,其中位于下方的蓝色曲线为干扰初步抑制率的变化曲线,上方红色为干扰融合抑制率变化曲线,可见融合抑制率较之初步抑制率高出20%左右,体现出了融合识别与抑制的优势,并且两条曲线随干噪比的变化不大,虽然干噪比会影响到雷达测速精度(对应峰值多普勒谱线位置的随机散布程度),但对于该干噪比较高的情况,其测量精度已足以满足本文方法对干扰所在DFT单元的确定和干扰信号峰值的识别,因此干扰抑制性能相对稳定。 图5 干噪比对干扰抑制率的影响Fig.5 Influence of JNR on jamming suppression rate 其他条件同第5.1节不变,改变速度随机扰动误差标准差,使其从0 m/s逐渐增大到0.25 m/s,得到结果如图6所示,可见初步抑制率和融合抑制率均随着速度随机扰动误差的增大而降低,这是由于随机性的增大使得虚假目标多普勒域峰值落到估计的DFT单元内的概率降低,尤其对于干扰初步抑制,其原理是基于假目标的多普勒频率分布特性,速度随机扰动会对其抑制效果产生直接影响,但是随着幅度信息的引入,采用融合抑制的方法会使效果得到明显改善。 图6 速度随机扰动标准差对干扰抑制率的影响Fig.6 Influence of stochastic perturbation standard deviation onjamming suppression rate 其他仿真条件不变,改变真实目标与虚假目标(径向速度为5 m/s)的径向速度差异,使其从0.4 m/s逐渐增大到1 m/s,分别针对快起伏和慢起伏两种情况,计算本方法对真实目标的错误抑制率。 仿真结果如图7所示,可见对于两种起伏特性的目标,总体错误抑制率差异不大,并且随着速度差异的增大,错误抑制率呈下降趋势,并且大多处于7%左右,其实在某个CPI内对真实目标的误判和抑制并不一定会对整体态势判别产生太大影响,因为在其他扫描周期中真实目标的径向速度会存在一定的变化,与虚假目标的径向速度差异相对较大,使其更易被鉴别,从而能够在一定程度上保证点-航迹数据处理的连贯性。 图7 真-假目标速度差异对真实目标错误抑制率影响Fig.7 Influence of value difference between true target and the false target on the true target wrong suppression rate 仿真条件与第5.1节中相同,采用MTI的方法对干扰进行抑制,实际抑制效果如图8所示,虽然在低频部分(对应径向速度较小的情况),信号幅度有所减小(对比图2),但仍然能够超过检测门限。 图8 MTI抑制效果Fig.8 Jamming suppression result of MTI 可见:在密集假目标干扰具有多普勒调制特性的情况下,采用MTI对干扰的抑制效果十分有限,与本文方法相比,本文方法对密集假目标干扰的抑制具有较大优势。 本文在分析密集假目标干扰运用特点的基础上,结合虚假信号的多普勒频率分布特征和幅度统计特性,提出了基于信号-数据多特征的密集假目标干扰融合识别与抑制技术,本方法通过对多个特征的提取,增加了识别干扰的信息维度,提高了识别的稳定性和正确率,改善了具有多普勒调制信息的密集假目标干扰抑制效果,仿真试验表明与MTI相比本方法在干扰抑制方面具有一定的优势。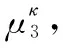
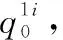
3.4 基于D -S证据理论的干扰融合判别与抑制
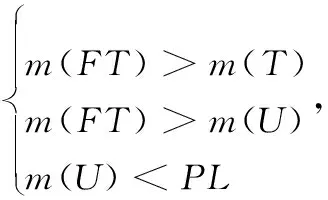
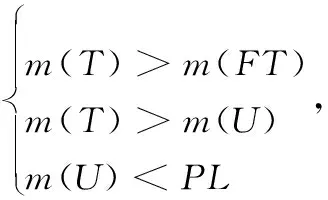
4 算法流程
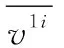
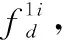
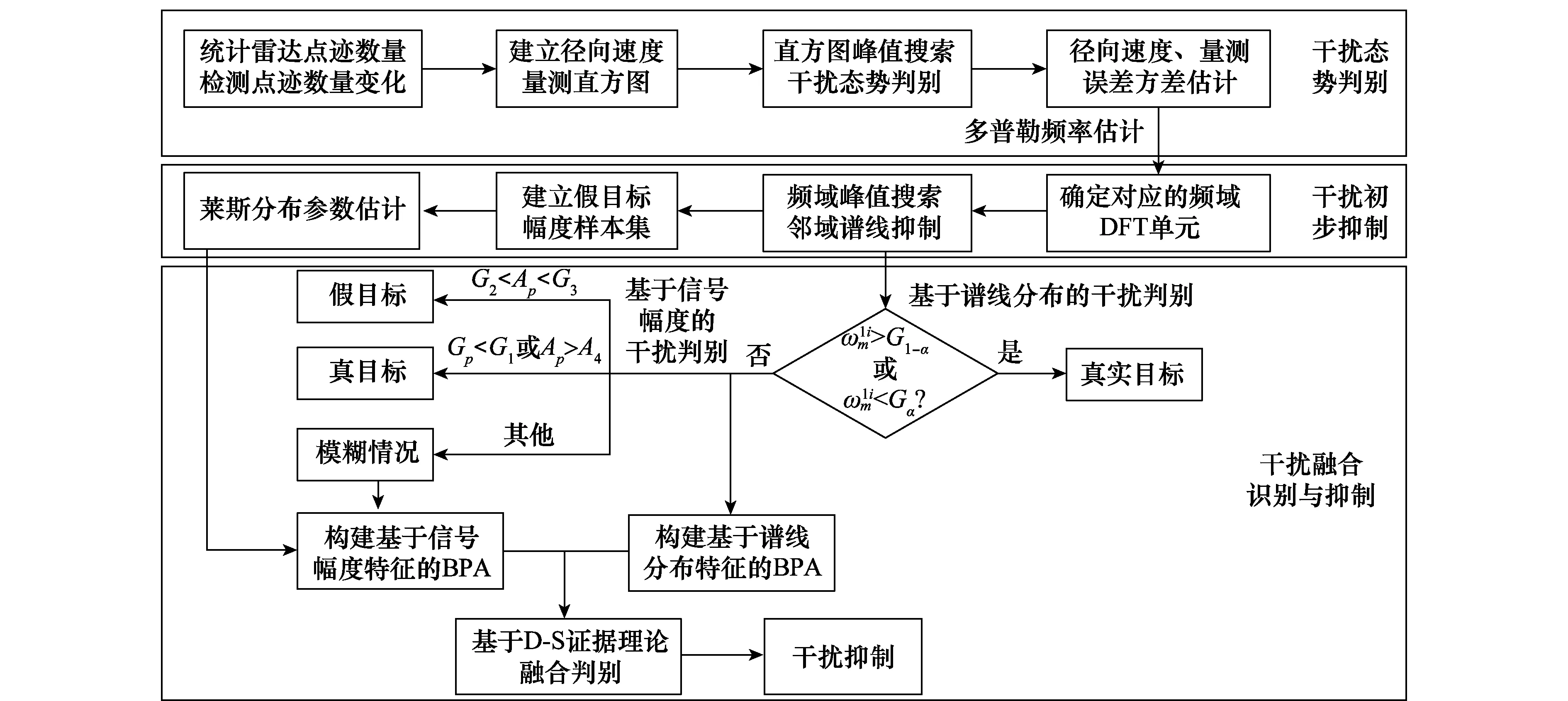
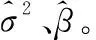
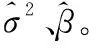
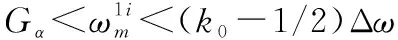
5 仿真实验
5.1 仿真实验1
5.2 仿真实验2
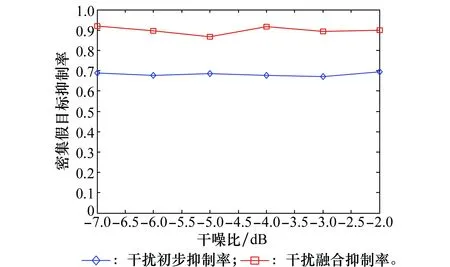
5.3 仿真实验3
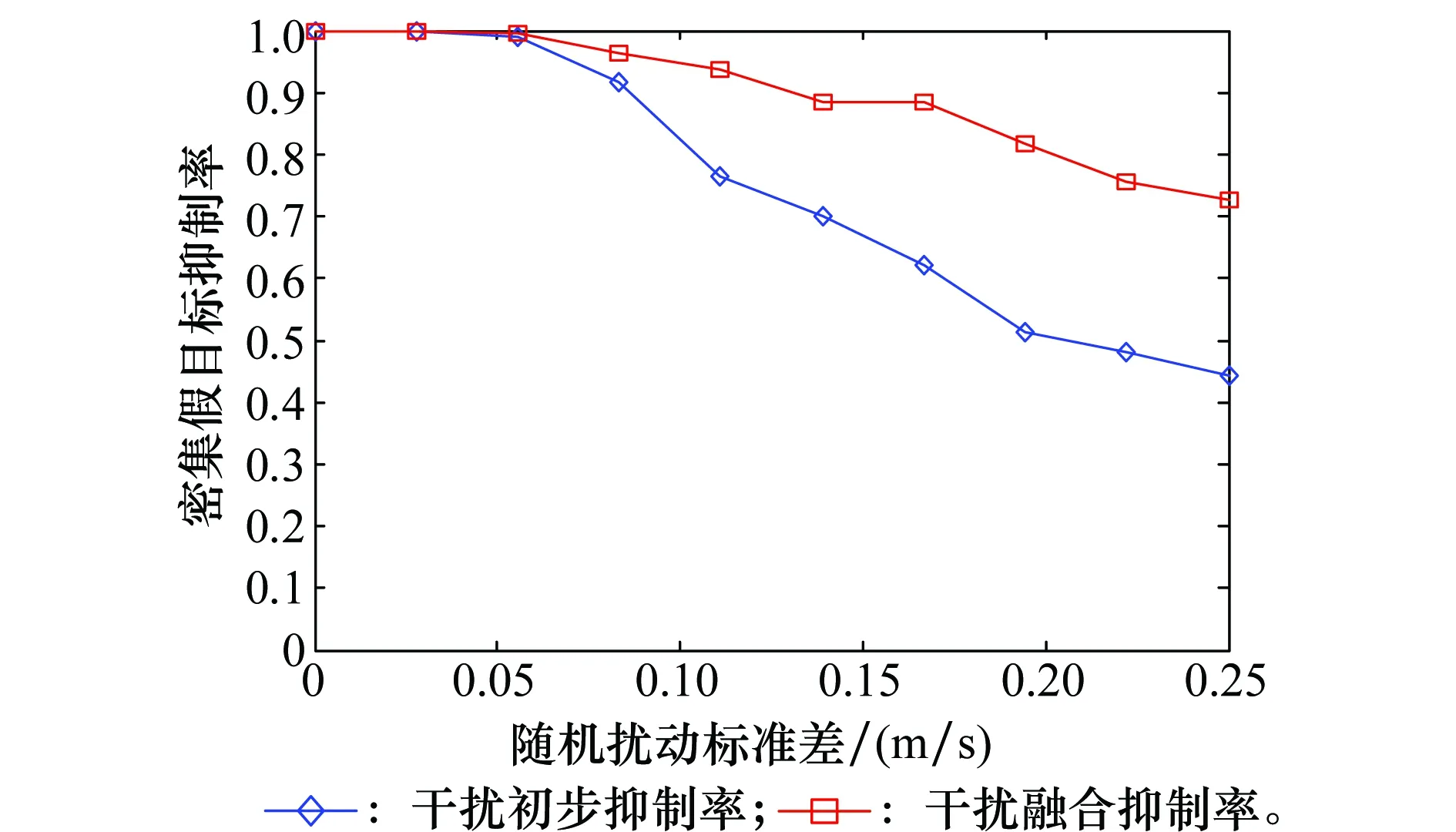
5.4 仿真实验4
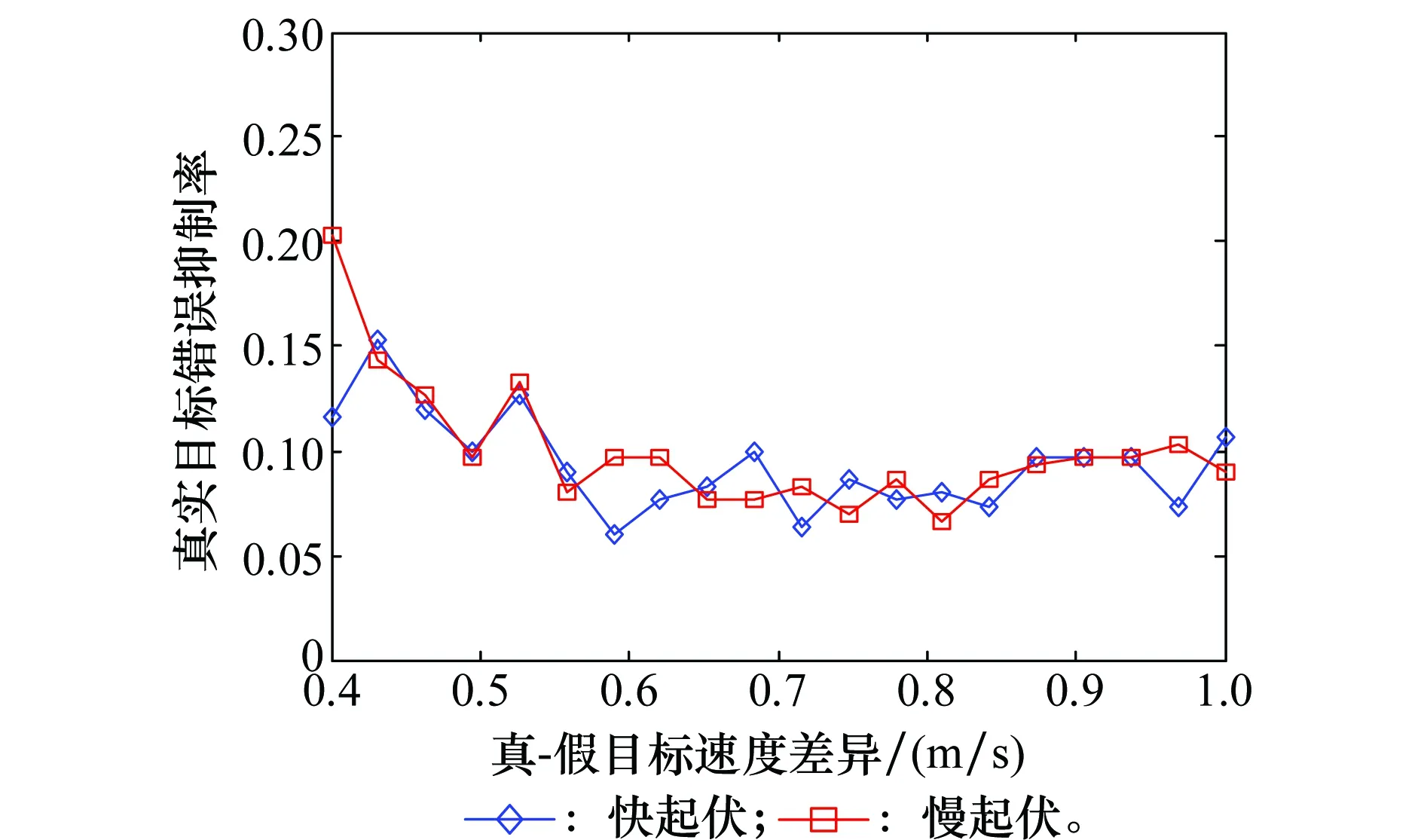
5.5 仿真实验5
6 结束语
