利用径向速度的Kalman-PDA滤波算法

刘 代, 赵永波, 高 剑, 李 伟

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 西安电子工程研究所, 陕西 西安 710100)

0 引 言

在雷达数据处理中,将概率数据关联法(probabilistic data association, PDA)算法和Kalman滤波算法相结合使用越来越广泛[1-5]。PDA算法能在跟踪波门内对多个过门限的量测数据进行数据关联,确定各个量测来源于目标的概率,并利用其对新息加权获得目标的状态估计。在雷达目标跟踪中,Kalman滤波算法是最小方差意义下的最优算法[6]。将PDA算法与Kalman算法结合使用很好地得到目标的状态估计并使目标的最小方差最优。文献[1-5]将PDA算法和Kalman滤波算法相结合应用到MUSIC信号处理、码分多址(code division multiple access, CDMA)通信和多输入多输出(multiple-input multiple-output, MIMO)信道,得到很好的滤波效果。文献[7]利用径向速度观测误差与距离观测误差相关条件下,提出序贯处理的滤波算法。文献[7-8]只是在Kalman滤波中引入了径向速度,却没有利用更加准确的动目标检测(moving targets detection, MTD)测出的径向速度,未与PDA算法结合使用。目前解MTD速度模糊方法较多[9-13],本文基于MTD测出的不模糊径向速度,提出了一种利用径向速度的Kalman-PDA算法(定义为KalmanV-PDA),利用此径向速度建立速度波门,推导了速度波门表达式,在量测方程中引入径向速度维,利用MTD测出的径向速度实时更新目标观测值中的径向速度,而不是利用目标三轴速度和位置的数学表达式来计算量测径向速度。利用径向速度的Kalman-PDA算法相比标准的Kalman-PDA滤波算法目标跟踪性能得到很大提升。

1 数学模型

假设目标在XYZ平面内做匀速直线运动。其状态方程为

xk=Fk|k-1xk-1+wk-1

(1)

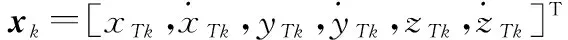
目标量测模型

zk=h(xk)+vk

(2)

式中,zk为k时刻的观测值,zk=[xTk,yTk,zTk,vrk]T,xTk=rTkcosθTkcosφTk,yTk=rTksinθTkcosφTk,zTk=rTksinφTk,rTk为k时刻雷达测得的目标径向距离,θTk为k时刻雷达测得的目标方位角,φTk为k时刻雷达测得的目标俯仰角,在目标观测模型中增加径向速度维,构成了四维观测向量,vrk代表目标径向速度；h(·)表示观测函数；vk为k时刻的观测噪声,其协方差矩阵为R。

2 标准Kalman-PDA滤波算法

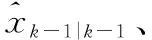
步骤1预测k时刻目标的状态

(3)

步骤2计算第i个测量值对应的新息

(4)

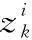
计算真实新息协方差矩阵:

(5)

式中,Hk=(ΔxkhT(xk))T为雅克比矩阵;Rk为k时刻的测量误差协方差矩阵。

计算状态预测协方差矩阵：

pk|k-1=FPk-1|k-1FT+Qk-1

(6)

步骤3计算第i个量测值源于目标的条件概率βi[15]

(7)

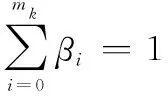
步骤4根据计算的条件概率βi,将各个观测的新息进行组合

(8)

即可获取目标状态的滤波结果：

(9)

滤波器的增益矩阵：

(10)

步骤5计算滤波后的状态协方差矩阵

Pk|k=[I-KkH]Pk|k-1

(11)

上述算法是将标准Kalman滤波算法与PDA算法结合起来使用,PDA算法做数据关联, Kalman滤波做均方误差最小收敛。

3 利用径向速度的Kalman-PDA滤波算法

3.1 MTD测速精度分析

脉冲多普勒(pulse Doppler, PD)雷达是一种常用雷达体制,利用多普勒效应检测目标信息,利用相参处理的方式提取目标径向速度。采用窄带多普勒滤波器组覆盖整个多普勒频率范围,如图1所示。窄带多普勒滤波器组可以通过快速傅里叶变换完成。

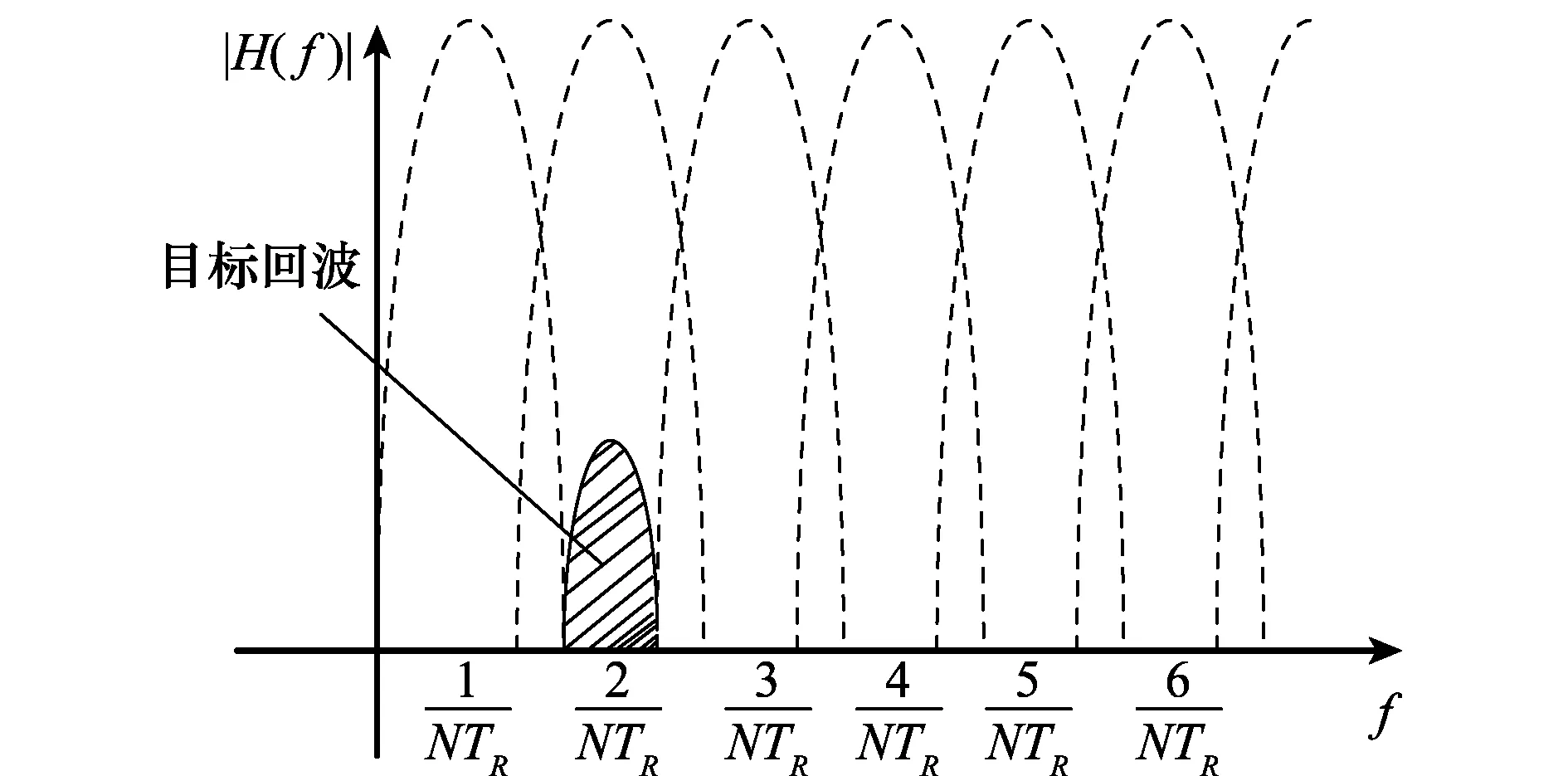
图1 多普勒滤波器组特性Fig.1 Characteristics of Doppler filter bank

假设多普勒通道个数N,目标的回波位于M号滤波器,脉冲重复周期TR,相参处理周期为CPI,脉冲重复频率fr, 脉冲重复周期为PRT,雷达载频fc,雷达波长λ,电磁波传播的速度c,可以得出:

目标的多普勒频移为

(12)

目标的径向速度为

(13)

MTD测速最大不模糊速度为

(14)

MTD测速精度为

(15)

通过上面公式可以看出只要选择合适的雷达载频和和脉冲相参处理周期就能保证MTD测速具有很好的测速精度,通常雷达设计时MTD测速精度都较高。

3.2 径向速度波门

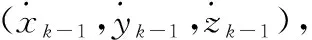
目标k时刻径向速度与k-1时刻径向速度差值为

(16)

假设k-1时刻目标速度为vk-1,则

(17)

代入式(16)可得

(18)

则径向速度差值波门为

(19)

式中，vmax为目标最大运动速度。

3.3 对目标观测函数线性化

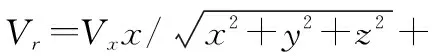
Zk|k-1=H(k)Xk|k-1+Vk

(20)

其中

3.4 利用径向速度的Kalman-PDA算法

在KalmanV-PDA算法中用MTD测出的径向速度和目标位置信息组成目标观测值zk=[xTk,yTk,zTk,vrk]T,其中(xTk,yTk,zTk)为k时刻目标在直角坐标系中的坐标,Vrk为k时刻MTD测出的径向速度,zk是由1,2,…，lk个观测值组成。

利用KalmanV-PDA算法步骤如下:

步骤1预测k时刻目标的状态

(21)

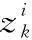
计算第i个测量值对应的新息:

(22)

计算真实新息协方差矩阵:

(23)

计算状态预测协方差矩阵:

pk|k-1=FPk-1|k-1FT+Qk-1

(24)

步骤3计算第i个量测值源于目标的条件概率βi[15]

(25)

步骤4根据条件概率βi,将各个观测的新息进行组合

(26)

目标状态的滤波结果:

(27)

滤波器的增益矩阵

(28)

步骤5计算滤波后的状态协方差矩阵

Pk|k=[I-KkH]Pk|k-1

(29)

4 实验结果分析

为了验证文中所提KalmanV-PDA算法的有效性,本文进行了如下场景仿真,假设目标远离雷达飞行,从初始位置为(12 000 m,12 000 m,1 000 m)飞出,X轴方向速度200 m/s,Y轴方向速度100 m/s作匀速直线运动,高度保持1 000 m不变。雷达相参处理周期(coherent process interval recurrence, CPI)为80 ms,脉冲重复频率(pulse recurrence frequency,PRF)为1 kHz,雷达载频fc为2 000 MHz,电磁波传播的速度c为3×108m/s,每1 s观测一次数据,观测时间为100 s。则MTD测速精度为0.937 m/s,仿真中取测量距离、方位角误差分别为50 m和8 mrad,径向速度误差分别取1 m/s和5 m/s。作200次蒙特卡罗仿真。目标状态转移矩阵为

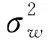
将本文提出的KalmanV-PDA与标准Kalman-PDA滤波算法进行了对比,分别从目标位置的均方根误差(root mean square error, RMSE)和速度RMSE以及收敛速度三方面进行了对比,从图3目标距离RMSE曲线可以看出KalmanV-PDA算法性能最好,具体体现在收敛速度最快,位置RMSE最小。从图4目标速度RMSE曲线可以看出KalmanV-PDA也是性能最好的,具体体现在目标速度的RMSE最小,收敛速度最快。

本文分析了MTD测速误差对算法的影响,从图3和图4可以看出在测速误差取为测速精度的5倍时,KalmanV-PDA算法比标准Kalman-PDA滤波算法性能优越,MTD测速误差对滤波算法性能影响较小,可以忽略不计。分析KalmanV-PDA算法性能好的原因就是由于采用MTD检测出的目标精确径向速度,更新了观测方程中的目标观测值,提高了目标跟踪性能。

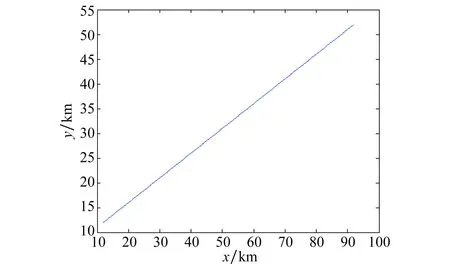
图2 目标运动轨迹Fig.2 Motion trajectory of target

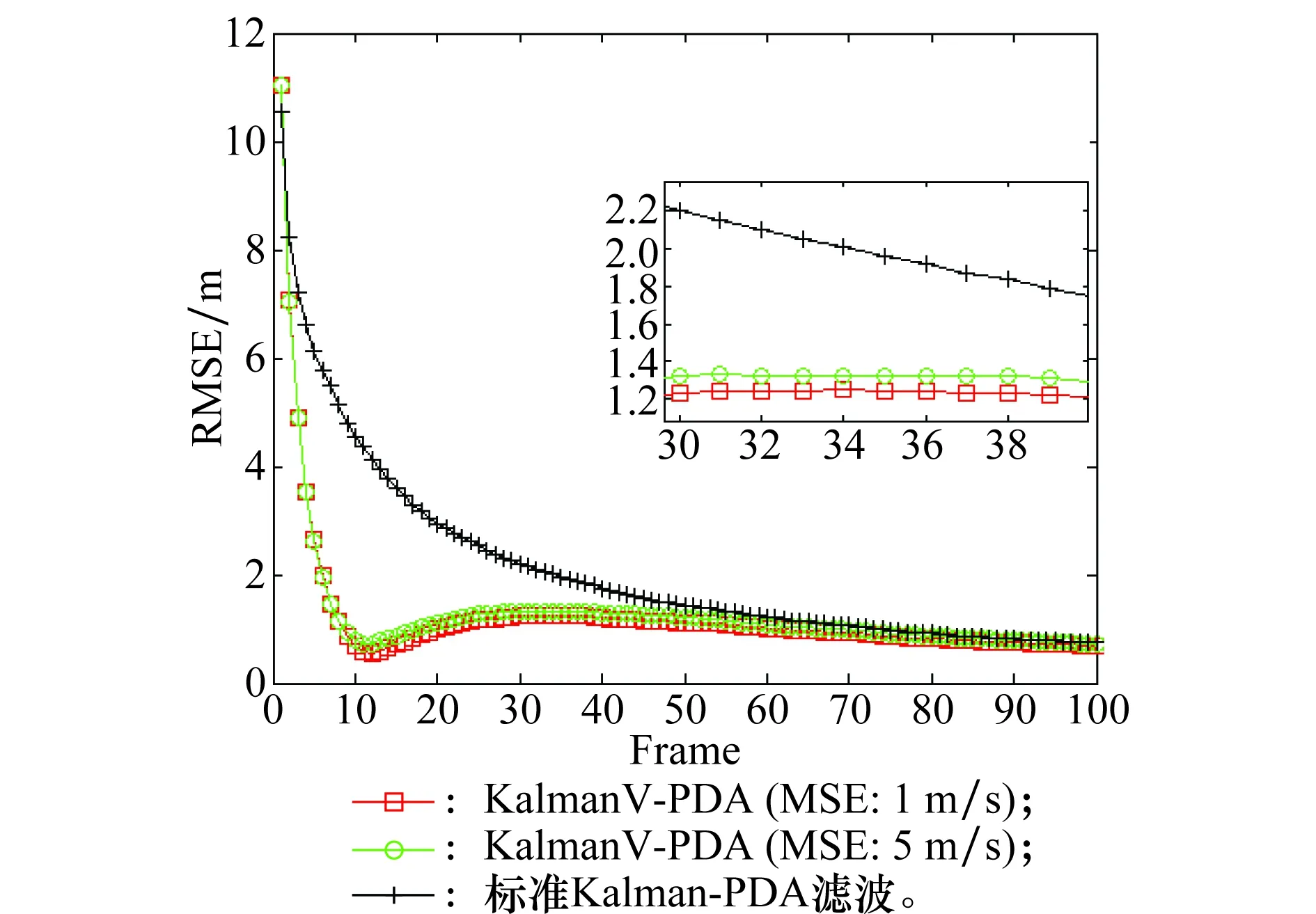
图3 目标位置RMSE曲线Fig.3 RMSE curve of target

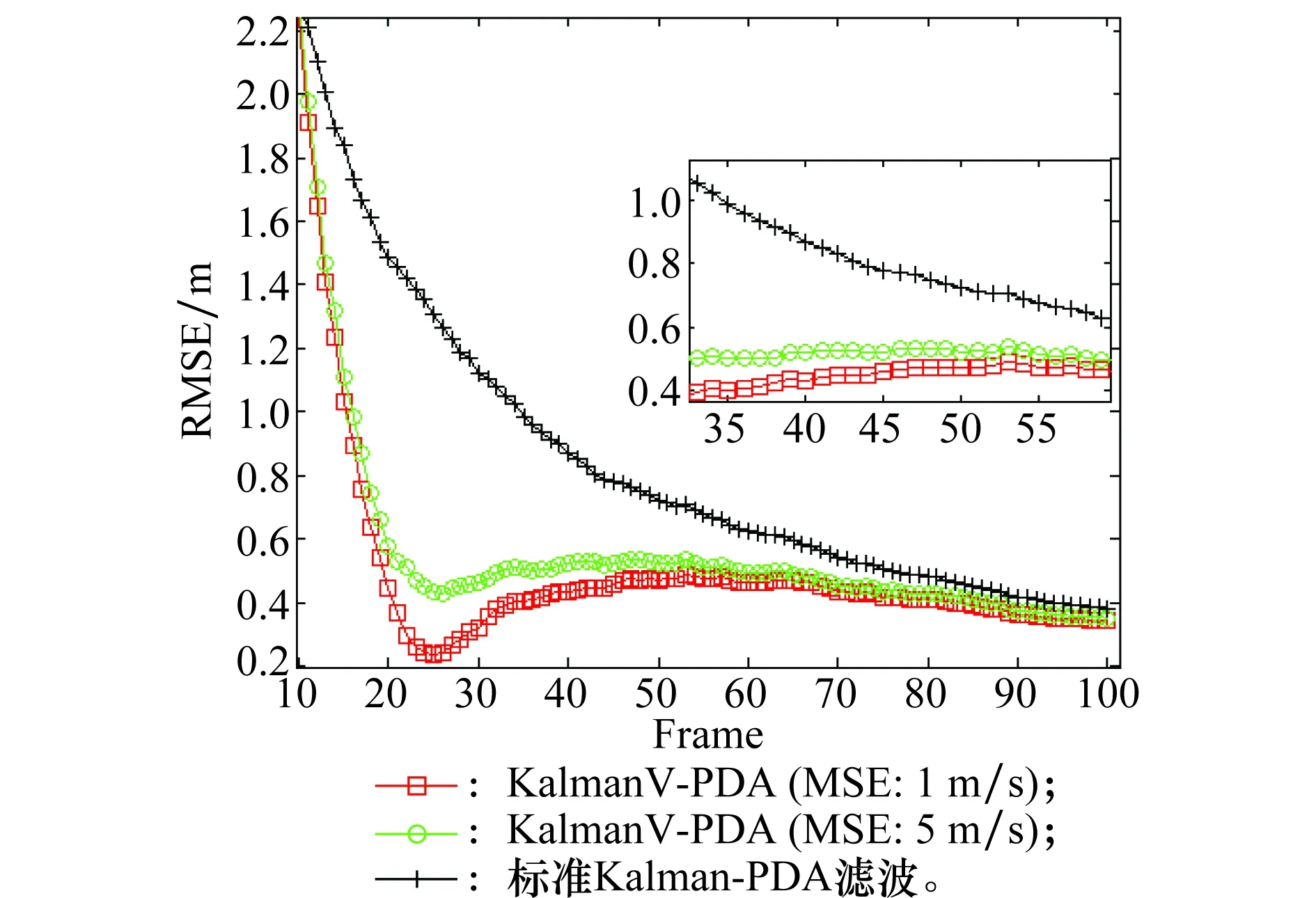
图4 目标速度RMSE曲线Fig.4 RMSE curve of target velocity

5 结 论

利用MTD测速的KalmanV-PDA算法,相比标准的Kalman-PDA算法,收敛速度快,目标位置RMSE和速度RMSE小,提高了目标预测精度,改善了目标跟踪性能,而且通过分析 MTD测速误差对跟踪性能影响较小。利用径向速度波门可以应用到航迹相关中,这可以作为后续研究内容。