微型电动货车车架分析
2018-10-15周辉赵海军程广伟宋伟志姚永玉
周辉,赵海军,程广伟 ,宋伟志 ,姚永玉
(1.洛阳理工学院机械工程学院,河南洛阳 471023;2.天津职业技术师范大学汽车与交通学院,天津 300222)
0 引言
当今能源危机、大气污染严重,特别是城市区域,交通拥堵、人员密集,各地相继推出限行政策,传统微型货运车辆在城区的使用受到了诸多限制,对城区物流影响较大。微型电动货车对于缓解城市交通污染,提高城市物流运输效率,有非常现实的意义。而车架作为主要承载部件,需承受扭转、弯曲、振动冲击等复杂载荷,其足够的强度、刚度及动态特性对于保证整车使用性能及安全性十分重要[1-2]。文中以在某传统微型货车基础上改装的电动货车为基础,对改装后的车架进行受力分析及有限元仿真,初步验证了车架的强度和刚度,进行了模态和谐响应分析,可为车架改进提供依据,以保证车辆的可靠性。
1 车架有限元模型建立
建立改装后的微型电动货车车架三维模型,如图1所示。

图1 车架三维模型
该车架为边梁式车架,由2根纵梁和6根横梁构成,纵横梁之间采用焊接。车架材料为B510L钢,纵梁为箱形截面,前横梁为槽形截面,其余横梁为圆形截面。其中纵梁厚度为3.5 mm,第一横梁厚度为2.5 mm,其余横梁厚度为4 mm。改装车架去掉了原车底盘发动机部分及发动机悬置部分,增加电动机托架和电动机及其控制部分。在车架中部和后部用角铁(Q345)焊接电池箱,前电池箱通过2根厚度为4 mm的槽钢(Q345)固定在车架两纵梁上,后电池箱焊接在原固定燃油箱的横梁上。
在前处理软件中,将车架三维模型导入ABAQUS进行分析。因为车架各部件厚度远小于其整体结构尺寸,应用壳单元类型进行分析具有较高的准确度,所以车架结构采用壳单元模拟[3]。车架各部件连接时,采用焊接和螺栓连接及铆接,在建立有限元模型时不考虑具体连接性能,均采取刚性绑定约束。前悬架为麦弗逊悬架,用弹簧单元简化;后悬架为钢板弹簧悬架,采用刚性梁单元和弹性单元模拟。定义车架材料及各部件壁厚,材料属性如表1所示。网格划分以S4R四边形单元为主,S3三角形单元为辅,整个模型含24 832个节点、25 078个单元,其中四边形单元24 832个。有限元模型如图2所示。

表1 材料属性
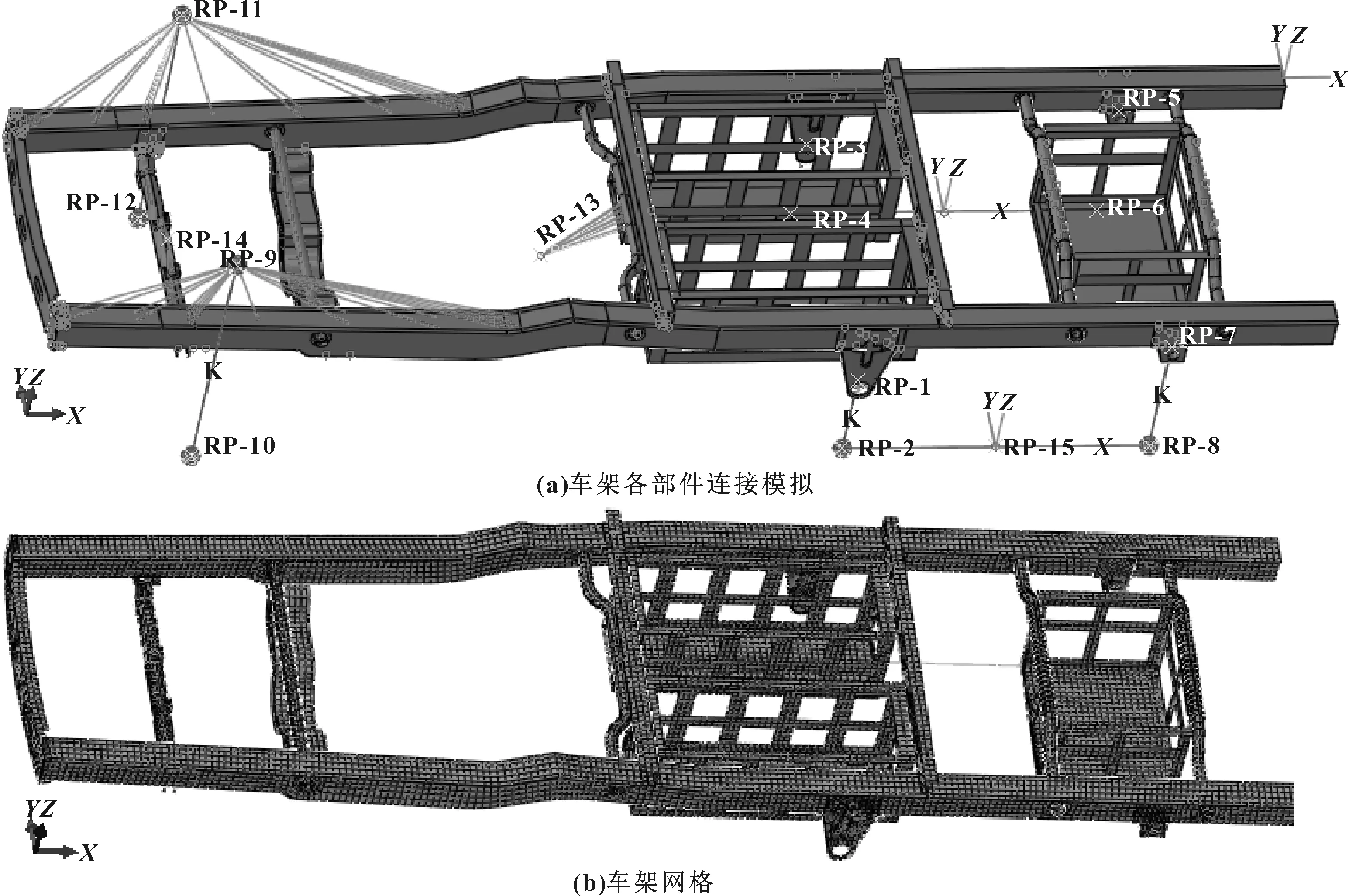
图2 车架有限元模型
2 车架静力学分析
2.1 静力学分析基础
文中所研究为线性静力学,不考虑惯性和阻尼,其基本有限元方程[4]为:
KU=F
(1)
式中:K为模型刚度矩阵;U为节点位移阵列;F为模型受外界力矩阵。
(1)强度计算基础
车架静强度校核根据第四强度理论,采用Von Mises等效应力来进行[4]。
Von Mises等效应力公式为:
(2)
强度合格条件为:
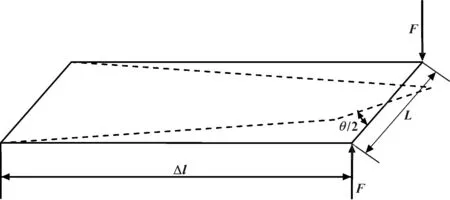
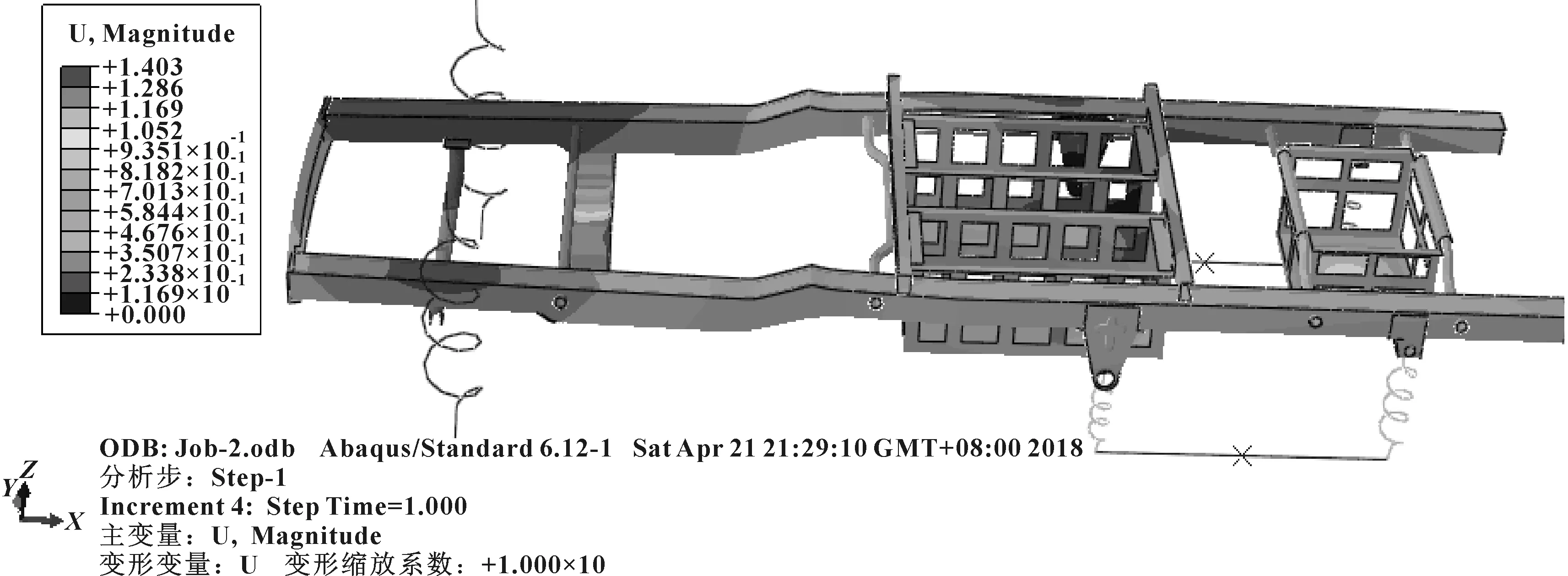
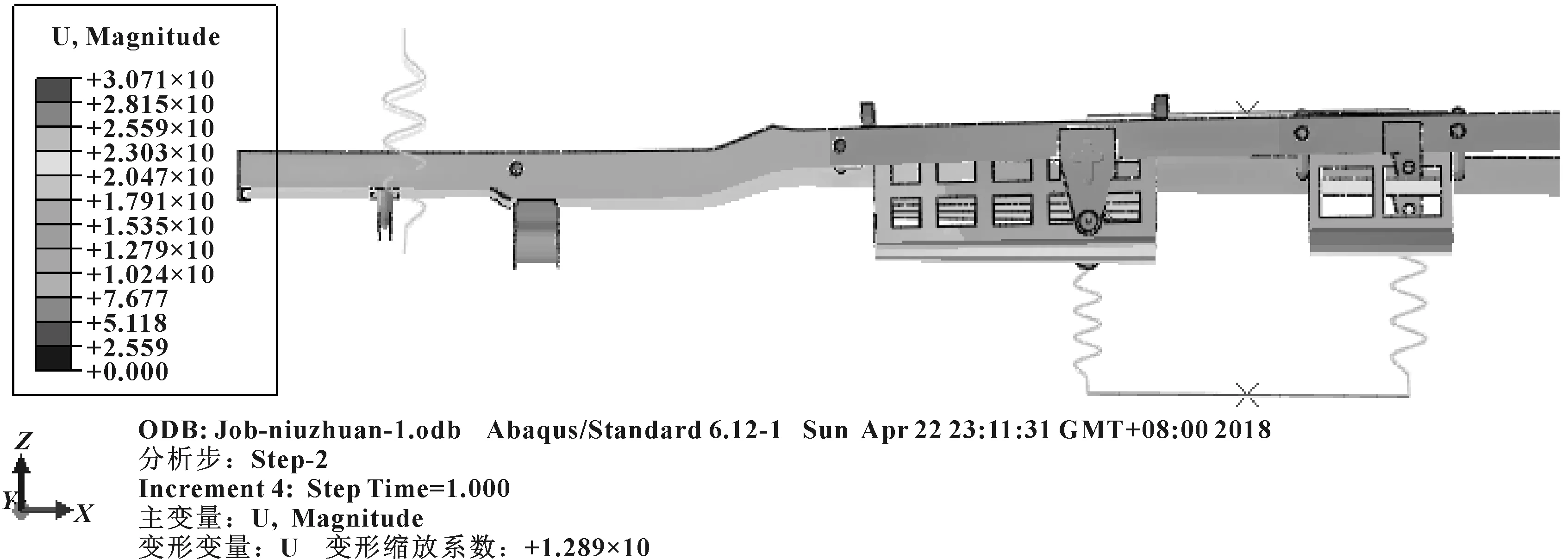
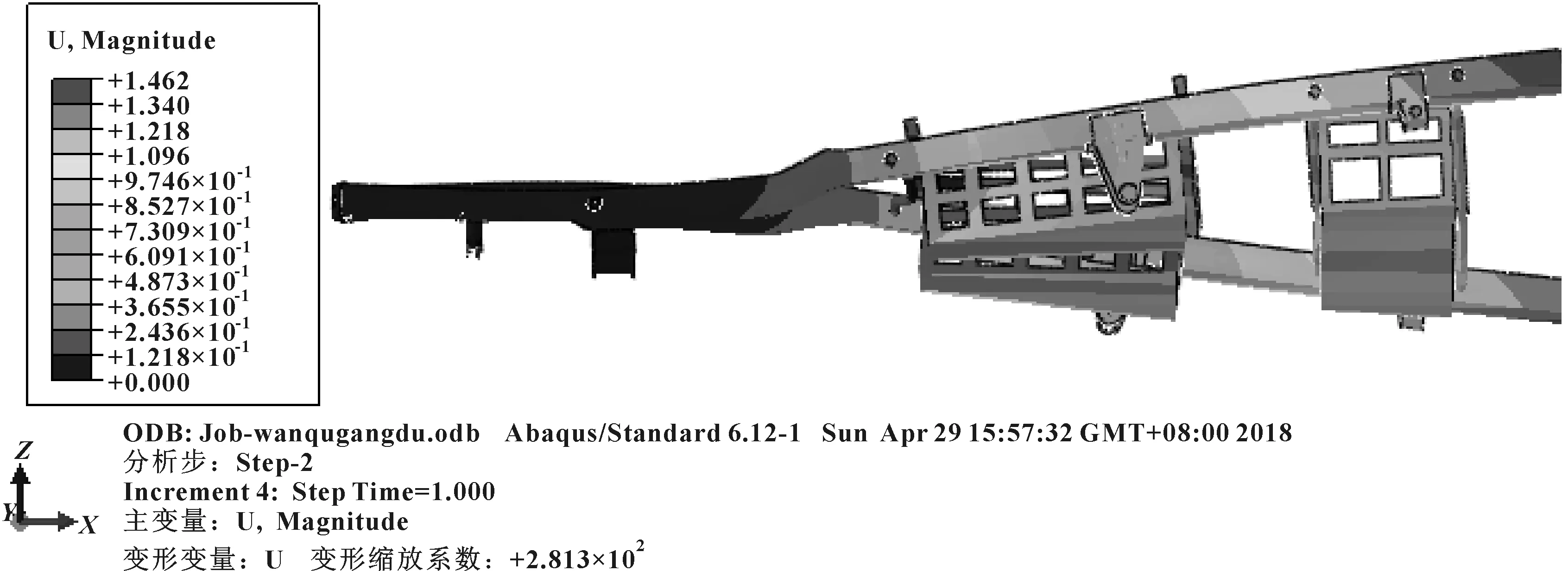
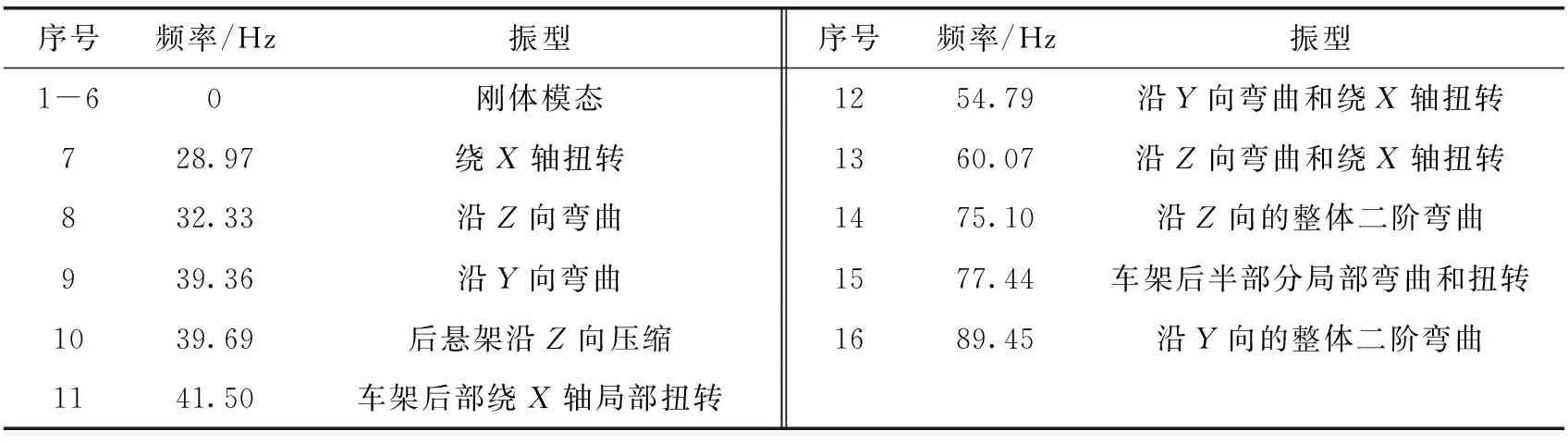
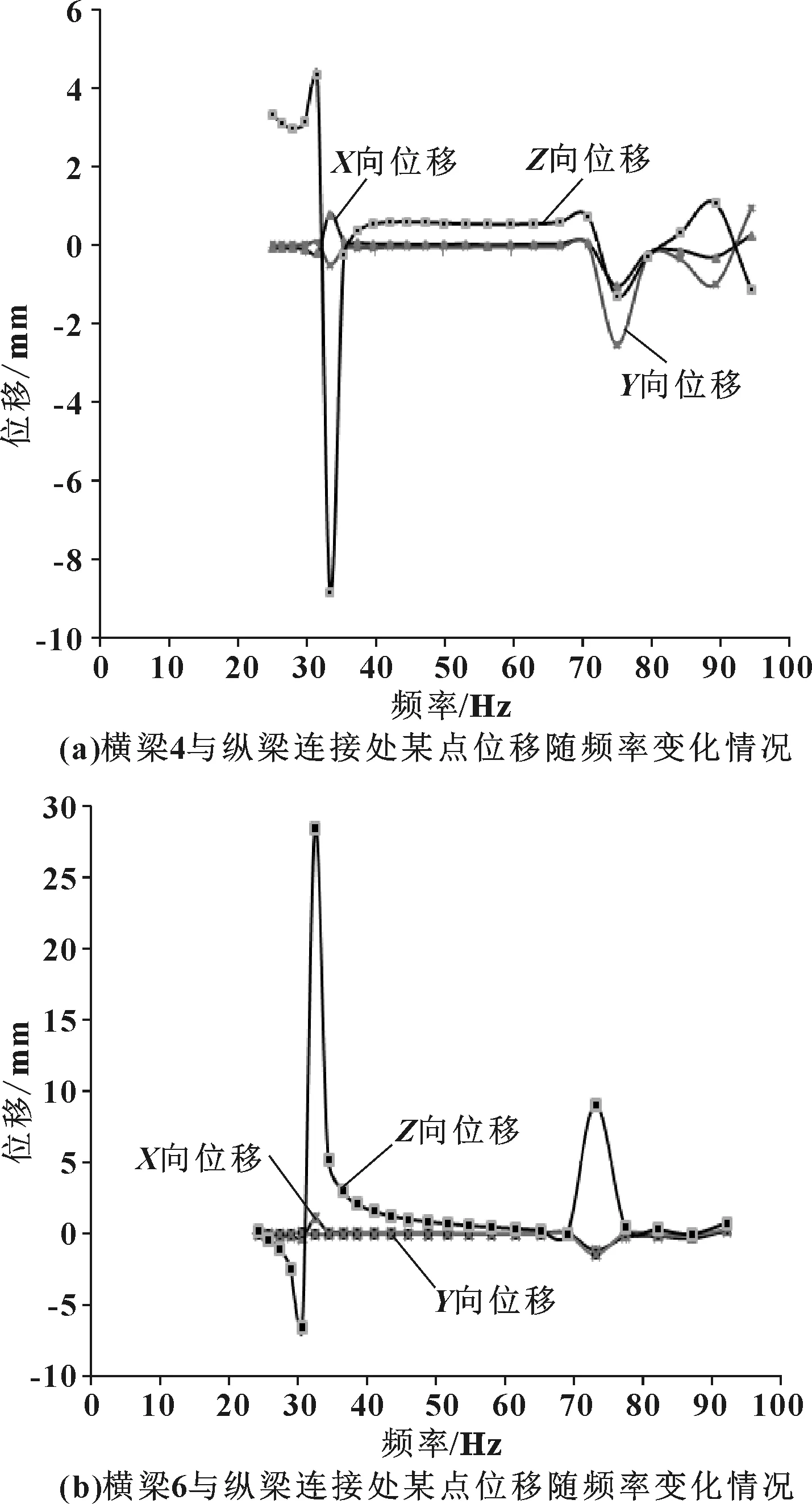
σr (3) 式中:σr为Von Mises应力;σs为材料屈服极限;n为安全系数。 (2)刚度计算基础 ①弯曲刚度 计算车架弯曲刚度时,将其简化为简支梁形式,如图3所示,在车架中部施加竖直向下的集中载荷,得出车架变形量dzmax。车架弯曲刚度根据式(4)求解[1]: (4) 式中:K′为弯曲刚度;Δl为两支撑点之间距离;F为竖直方向集中载荷;dzmax为挠度。 图3 车架弯曲刚度计算简图 ②扭转刚度 计算扭转刚度时,将车架简化为4根梁构成的矩形,约束前方两端点的竖直平动自由度,后方两端点施加方向相反大小相等的集中载荷,得出车架变形量。车架扭转刚度根据式(5)求解: (5) M=FL (6) (7) 式中:CT为扭转刚度;L为左右受力点之间距离;F为竖直方向集中载荷;d为挠度;θ为扭转角。 车架扭转刚度计算简图如图4所示。 图4 车架扭转刚度计算简图 车架载荷包括自重和承载各总成重力。承载各总成主要包括电动机及其控制系统、动力电池总成、变速器总成、车厢、驾驶室、货物、乘员等。各载荷重力及有限元分析时处理方式如表2所示。 表2 车架静态载荷及处理方式 车辆在定型试验中必须要模拟典型工况以确定车辆的行驶可靠性,通常包含弯曲、扭转、紧急制动和转弯4种工况。其中弯曲和扭转工况反映了车架的结构强度,文中主要分析这两种工况。其边界条件定义如表3所示。 表3 扭转、弯曲工况边界条件 (1)弯曲工况 弯曲工况以车辆满载情况进行分析,考虑车辆行驶状态,进行校核时要乘以动载系数。相关资料表明,动载系数一般取2~2.5,文中取2.5[5]。 弯曲工况车架应力情况如图5所示,变形情况如图6所示。从图中可得,最大变形出现在电机托架处为1.403 mm;应力最大值出现在电机托架弯曲点,达到83.82 MPa,乘以动载系数后为209.55 MPa小于许用应力,满足强度要求。除此之外,车架整体受力均匀,且等效应力大多在20 MPa以下,针对电机托架应力集中处,可在背部焊接加强肋。 图5 弯曲工况车架应力图 图6 弯曲工况车架变形云图 (2)扭转工况 扭转工况以车辆满载情况进行分析,受力及前轮边界条件和弯曲工况相同,左右后轮分别施加±20 mm位移约束。电动货车主要在市区道路工作,在扭转工况下车速一般较低,动载系数一般取1.3[7]。经计算,车架满载扭转工况下的变形情况如图7所示,左后悬架位移最大,达到30.71 mm,左右车架纵梁变形量差值7.68 mm。车架所受应力情况如图8所示,最大应力出现在后悬架前支座处,应力达到222.4 MPa,是因为在建立有限元模型时,将悬架与支座直接进行了刚性耦合造成了应力集中。实际钢板弹簧与支座之间连接允许相对滑动,可避免应力集中问题。除此之外,焊接前电池箱的槽钢和纵梁连接处,以及焊接后电池箱的第5、第6横梁处受力相对较大,应力值在 75~130 MPa之间。考虑动载系数后应力值在97.5~169 MPa之间,小于许用应力。 图7 扭转工况车架变形图 图8 扭转工况车架应力图 (1)弯曲刚度 约束前悬架螺旋弹簧与车架连接处XYZ的平动自由度,约束后悬架两支座中间与后轮轴线对应处支座的YZ两个方向平动自由度,释放X方向自由度。如图3所示,将车架简化为简支梁,在约束的前后两支座中间左右纵梁上分别施加500 N的作用力。弯曲变形情况如图9所示,dzmax为0.48 mm,Δl为2 487.2 mm,根据公式4计算得到弯曲刚度K′为3.3×105N·m2。某电动车车架弯曲刚度[5]为99 307 N·m2,与之相比文中所研究改装后的电动货车刚度值更为合理。 图9 弯曲刚度车架变形图 (2)扭转刚度 计算扭转刚度时,约束前悬架螺旋弹簧与车架连接处XYZ的平动自由度,在左右纵梁后悬架两支座中间与后轮轴线对应处支座上施加方向相反的500 N作用力。车架扭转变形情况如图10所示,受力点相对位移为2.92 mm,两受力点之间距离为976 mm。根据式(5)—(7)计算得,车架所受转矩M为488 N·m,扭转角为0.002 99 rad,扭转刚度为163 210.7 N·m/rad。 图10 扭转刚度车架变形图 为保证电动货车承载的可靠性,其车架不仅要有足够的静态强度和刚度,还需要有良好的动态性能。汽车在行驶过程中不仅要承受路面经车轮传递的随机振动[6],还要承受由电动机及变速器等工作时产生的周期性受迫振动。若车架某阶固有频率与其所受激振频率接近时,可能会发生共振,产生剧烈振动而造成车架过早损坏。因此,通过模态分析得到车架各阶固有频率为设计提供参考,避开外部激振频率,可以有效避免该问题发生。 完全按照车架的实际工况约束边界条件来进行模态分析,对于多自由度复杂系统来说是比较困难的[7]。从理论上讲,任意边界条件约束下的动态特性可以由自由边界条件下模态参数经计算得到[8]。因此,文中计算了自由边界条件下的车架模态,采用的方法为Lanczos法,结果如表3所示。 表3 车架前16阶去除前6阶固有频率及振型 汽车在行驶过程中承受路面经车轮传递的随机振动频率一般为20 Hz左右[6]。电动机运转时对车架的激励作用一般很小,不予考虑[7]。车架前16阶振型频率在28.9~90 Hz左右,低阶模态与路面所产生的随机激振频率较接近,有可能产生共振。 计算车架在简谐激励下的稳态响应,求出其关键节点的位移和应力变化情况,以验证车架改装的合理性,并为后续改进提供参考。谐响应分析时车架所受载荷和静态分析时相同,简谐激励通过前轮和后轮的Z向简谐位移约束实现。前后轮采用相同频率和振幅的简谐激励,后轮激励的相位角比前轮推迟π/6。电动货车主要在市区行驶,路面情况较好,激励的幅值取为20 mm。考虑车架前16阶模态(去除前6阶)频率范围,取激励频率范围为25~95 Hz,间隔为2.5 Hz,共29个激振频率。 由于电池重力较大,前后电池箱固定位置的谐振情况是需要关注的。在前后电池箱固定位置的纵横梁连接处选择相应节点来进行分析,其位移随激励频率的变化情况如图11所示。由图11(a)可知,横梁4与纵梁连接处节点位移在X向位移最大值为1 mm,Y向位移最大值为2.5 mm,且对应频率均在75 Hz附近,该频率大约对应车架14阶模态频率。Z向位移在低频阶段均较大,最大值出现在33 Hz附近,位移为8.8 mm,对应车架8阶模态频率。由图11(b)可知,横梁6与纵梁连接处节点位移在X向位移最大值为1.2 mm,Y向位移最大值为1.5 mm,对应频率也均在75 Hz附近。Z向位移在33 Hz下最大达到28.5 mm,75 Hz下达到9 mm。由此可知,所关注的纵横梁连接处,在33 Hz和75 Hz时谐振幅度较大。 图11 位移随激励频率变化情况图 在传统微型货车基础上建立了改装的电动货车车架有限元模型,充分考虑了车架结构特点,合理处理了各部件之间的相互作用关系。计算了电动货车车架强度和刚度等静态性能,计算了车架自由模态并进行了谐响应分析。综合得出如下结论: (1)按照静力学分析理论,车架弯扭强度均满足许用应力要求,弯扭刚度适中。但第5、第6横梁所受应力较大,可适当增加两横梁厚度。 (2)车架低阶自由模态频率与路面激励频率较接近,路面经车轮产生的激励可能会造成车架剧烈的振动。针对该情况,可适当调整电池箱固定位置。 (3)电池箱安装位置的纵横梁连接点在33 Hz和75 Hz的激振频率下可能会发生共振。应对车架结构进行优化以避免共振发生。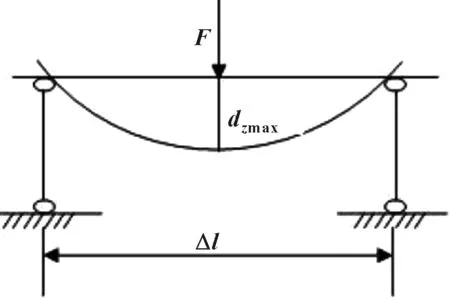
2.2 车架静态载荷

2.3 车架强度分析



2.4 车架刚度分析

3 车架动态特性分析
3.1 车架模态分析
3.2 车架谐响应分析
4 结论
