线性二自由度车辆模型横摆角速度和转弯半径的计算方法改进

黄新，丁志中

(1. 芜湖技师学院，安徽芜湖 241000；2.合肥工业大学计算机与信息学院，安徽合肥 230009)

0 引言

汽车稳态转向特性的研究对于提高行驶安全性十分重要，稳态转向是指一种稳定的转弯状态，该状态下车辆的速度和转向角是定值，从而以固定的转弯半径转弯行驶[1]。一方面，这个固定的转弯半径越逼近实际的弯道半径，汽车的操纵稳定性越高，因此如何计算转弯半径，令其最大限度地接近实际弯道的半径尤其重要。另一方面，在自动驾驶技术中，车辆行车轨迹的准确预测是事关行车安全的重要问题，它可为自动驾驶决策系统提供重要的参考数据。直行车道上的行车轨迹可以由速度、加速度等参数给出较为准确的短时预测。由于弯道的场景相对复杂，行车轨迹预测需要探索更好的方法。

二自由度车辆模型作为汽车的基本转向操纵模型，虽然相对简单，但已能体现车辆操纵动力学的基本特征，构成了复杂操纵模型的基础。很多学者提出了利用二自由度车辆模型对稳态转向特性进行分析和研究[2-7]，其中文献[4-7]中利用二自由度车辆模型给出了稳态转向特性下横摆角速度和转弯半径的计算公式，但都是在假设前轮转角比较小的情况下通过近似处理得到的。当前轮转角较大时，按照上述文献所给公式计算得到的转弯半径过大，与实际车辆转弯的经验值偏差较大。

文中对经典文献中基于二自由度基本操纵动力学模型求出的稳态转向特性下横摆角速度和转弯半径的计算公式进行了修正，以使修正后转弯半径的计算结果更接近真实的弯道半径。

1 稳态转向横摆角速度计算修正

由文献[6]中可知在汽车参数已知的情况下，当车辆以一恒定速度进行稳态转向时，车辆的稳态转弯半径与横摆角速度有关，因此在对车辆的稳态转弯半径进行求解前，应首先求出横摆角速度。在二自由度模型建立的运动方程中，二自由度指侧向速度和横摆角速度，因此利用二自由度车辆模型求解横摆角速度，既可以简化计算又可以得到横摆角速度。

二自由度车辆模型是在相对合理的近似和假设条件下简化的，此时车辆只具有侧向运动和横摆运动两个自由度[8]。这些近似和假设包括：车辆行驶于平坦路面、忽略与行驶动力学相关的垂向影响及耦合作用、车辆结构是刚性的等。

图1是简化的汽车二自由度模型，其中点O′是汽车转弯中心，R是转弯半径，点O是汽车的运动质心，β是汽车质心侧偏角，δ是汽车前轮转角，ωr是汽车横摆角速度，v是汽车质心行驶速度，vO是汽车质心处的纵向速度分量，uO是汽车质心处的横向速度分量，u1、u2分别是汽车前、后轮中心的速度，α1、α2分别是前、后轮的侧偏角，Fy1、Fy2分别是前后轮所受的侧向力，a、b分别是质心到前后轮轴心的距离，L是汽车轴距。

图1 二自由度车辆模型

由牛顿第二定律和转动定律可得：

(1)

当前轮转角比较小时，侧向力与侧偏角呈线性关系[9]：

Fyi=ki·αi(i=1,2)

(2)

其中：ki是侧偏刚度，在两轮模型下分别为一个前轮或后轮侧偏刚度的两倍。

结合图1的角度关系以及利用近似分析法，可得到侧偏角与横摆角速度以及质心侧偏角的关系式(详细推导过程见文献[10])：

(3)

(4)

因此，式(1)可化为：

(5)

分析式(5),当整车参数m、a、b、k1、k2被给定的情况下，此时两个方程组对应三个未知数质心侧偏角β、横摆角速度ωr、加速度ay。当未知数个数大于方程个数时，方程的解不是唯一的而是无穷解，此时加速度ay可以利用固结于汽车的车辆坐标系分析求解。

如图2所示，将沿弯道行驶的汽车看成是质心运动，为了便于分析比较(t+t)时刻相对于t时刻y轴方向的速度增量，先将(t+t)时刻的速度按照固结于(t+t)时的车辆坐标系分解，再利用与t时刻固结于车辆的坐标系平行的坐标系进行分析(参见图2中左上坐标系图)。

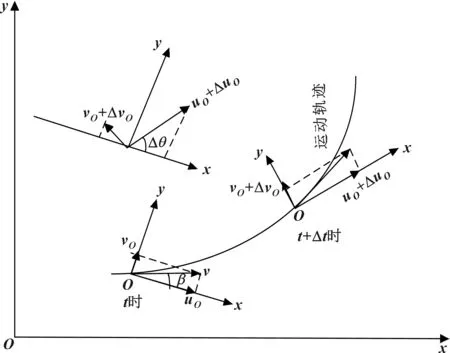
图2 汽车运动的坐标系

通过对图2中汽车由t时刻到(t+t)时刻的运动进行分析，得到加速度的表达式(详细推导过程参见文献[10])：

(6)

其中：ωr是横摆角速度。

将式(6)代入式(5)后整理得：

(7)

因为质心侧偏角β较小，可以认为：

vO=vsinβ≈vβ；uO=vcosβ≈v

(8)

同时考虑到汽车的稳定转向特性，可令：

(9)

因此式(7)可以进一步化简为：

(10)

式(10)中上下两式相减，可以解出β和ωr的关系为：

(11)

其中：L=a+b。将β代入式(10)可求得横摆角速度ωr，详细过程如下：

因此横摆角速度ωr的表达式如下：

(12)

其中

同时，结合内外部因素来看，许多大型重污染企业期望通过上市实现低成本融资、提升原始投资人的价值、获得资本市场上的强大收购能力、提升企业的知名度，在国家强制规定上市污染企业的年报必须对环境行为进行披露的情况下，为获得投资人的认可、成为股民的选择，企业迫于外界压力和自身需求，往往会在环境行为方面进行合理化投资。

(13)

而K为稳定性因数[9]，定义为：

(14)

至此给出了文中推导的稳态转向特性下的横摆角速度计算修正公式，下节利用该横摆角速度求稳态转向特性下的转弯半径。

2 稳态转向特性下的转弯半径

车辆在转弯时，驾驶员的操控就是使得汽车的自身转弯半径尽可能和弯道半径相吻合，以实现安全平稳的弯道行驶。因此，车辆转弯半径的计算非常重要，如果得到与实际弯道比较相符的半径，必然会提高稳态转向安全性。

文中对以往文献给出的转弯半径的计算公式进行了修正，不同于以往前轮转角较小的假设，求解出前轮转角较大时对应的转弯半径的计算公式，下面即是转弯半径的求解过程。

分析图1中角度关系以及利用三角函数的近似关系得到转弯半径的表达式如下(详见文献[10])：

(15)

而(α1-α2)是向心加速度的函数[9]，即：

α1-α2=αyLK

(16)

ay=vωr

(17)

因此，转弯半径为：

(18)

将ωr的表达式代入式(18)，得到转弯半径的最终表达式(19)，过程如下：

(19)

如果将K和K(δ)代入上式，R也可写为：

当δ很小，cosδ≈1，K(δ)=K，此时横摆角速度和转弯半径近似为：

(20)

(21)

式(20)和(21)是多数文献资料给出的横摆角速度和弯道半径计算公式[1,5,8,9]。可以看出，它是假定cosδ≈1，K(δ)=K时的近似，这一近似使得它只适合于前轮转角很小和车速较低的情形。式(12)和式(19)是本文作者在前轮转角比较大的情况下给出的分析结果。对比于(14)，这里将式(13)中的K(δ)称为“动态”稳定因数，它反映了前轮偏转角对于K值的影响。

3 静态与动态稳定因素影响下的仿真分析与比较

文中采用实车数据对横摆角速度和转弯半径进行数值仿真实验，整车参数具体数值如表1所示[11]。考虑到一些特殊场合，车速计算范围为0～200 km/h，间隔为5 km/h。

表1 仿真所用参数[11]

由前面分析可知，动态稳定因数与前轮转角有关，图3给出了动态稳定因数K(δ)随前轮转角变化的曲线，可以看出动态稳定因数随着前轮转角的增大而增大。

假定前轮转角δ为15°，对静态与动态稳定因数下的横摆角速度进行数值仿真实验。

图3 动态稳定因数K(δ)的变化曲线

图4是分别利用K和K(δ)计算出的横摆角速度。如图4所示，静态和动态稳定因数下的横摆角速度的变化趋势是一致的，但是数值上有细微区别，动态稳定因数下的横摆角速度总体上比静态稳定因数下的横摆角速度稍微偏小。不过总的来说，动态稳定因数K(δ)对于横摆角速度的影响并不明显。

图4 横摆角速度的计算对比

取前轮转角δ=15°，假定依据式(21)(即令cosδ=1)计算的转弯半径如图5所示。在车速分别为20,40,60,80,100,120 km/h时，转弯半径分别为23.1,68.1,143.3,248.5,383.7, 549.0 m。可以看到，所计算的转弯半径偏大。按照文中给出的计算方法式(19)，其结果如图6所示。

图5 依据式(21)计算的转弯半径

图6 依据文中修正后的公式计算的转弯半径

在车速分别为20,40,60,80, 100,120 km/h时，转弯半径分别为22.1,55.2, 91.8,122.9,146.7,164.4 m，根据实际行车过程中的驾驶经验，该计算结果与实际情况吻合度较好。图7给出的是这两种方法在城市道路限速值之下计算的转弯半径差别。可以看到，在20 km/h以下速度时两者计算结果比较接近，速度在40 km/h以上时，修正后公式所得值更为合理一点。

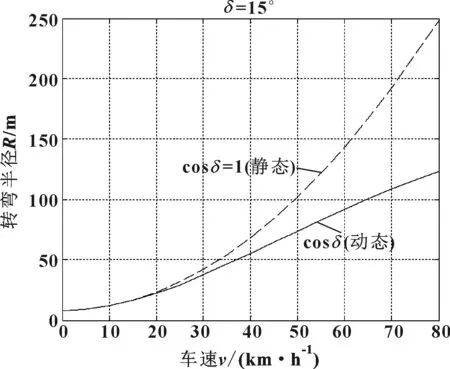
图7 中低速下转弯半径计算值对比

图8是利用文中提出的转弯半径的计算方法计算的δ为5°、10°和15°三个前轮转角下的转弯半径。

图8 不同转角下计算的转弯半径

在实际的驾驶中，当前轮转角比较小时，说明弯道比较平缓即弯道半径比较大，当前轮转角相对较大时，弯道相对急即弯道半径相对较小；当车辆以一固定前轮转角转动时，转弯半径越大即需要更高的车速才能提供足够的向心力不至于使车辆发生离心运动从而满足驾驶的安全性。如图8所示，当车辆以前轮转角δ=5°转向时，转弯半径随着车速的增大迅速增大，转弯半径相对较大；当车辆以前轮转角δ=10°和δ=15°转向时，转弯半径亦随车速的增大而增大，但增大的趋势相对较小，且转弯半径相对较小。由此可见仿真结果与实际驾驶情况基本一致。

图9给出了前轮转角为20°～45°时对应的转弯半径。然而如图9所示，当前轮转角较大且车速较高时，依据文中方法计算的转弯半径偏小，这是因为实际驾驶过程中，弯道比较急即转弯半径较小时需要较大的前轮转角，另外文中在对横摆角速度和转弯半径公式的修正中也采用了近似。

图9 大转角时采用K(δ)计算的转弯半径

4 结论

文中对多数文献中给出的二自由度车辆模型转向特性下的横摆角速度和转弯半径的计算公式进行了修正。由仿真结果可以看到，无论是否取cosδ≈1的近似，利用此方法所计算的横摆角速度差别并不大。动态稳定因数的引入主要改善了转弯半径的计算结果，使得转弯半径不再随车速呈现二次曲线上升的趋势。当车辆以固定的前轮转角转向时，多数文献给出的转弯半径的计算偏大，而经过修正后的转弯半径的计算能更真实地反映弯道半径。

需要说明的是动态稳定因数的引入虽然改善了前轮转角较小时的转弯半径，但是在前轮转角较大时反而使转弯半径偏小。