基于差分进化算法的再入可达域快速计算

2020-12-01蔺君何英姿黄盘兴

中国空间科学技术 2020年4期

蔺君，何英姿，黄盘兴

1. 北京控制工程研究所，北京 100190 2. 空间智能控制技术重点实验室，北京 100190

高超声速飞行器再入可达域又称作再入覆盖域，是指飞行器以给定的初始条件返回地球，到达着陆或者交班状态，飞行器所能允许的区域范围[1]。再入可达域是评估航程覆盖能力的指标，体现了飞行器的潜在飞行范围，可为飞行器任务规划和轨迹规划提供依据。

Vinh等在忽略了轨迹约束和哥氏力等理想情况下，计算最优落点方法，在此基础上，Doman和Ngo提出了次优落点区域的方法[2]。雍恩米等将再入可达域问题转化为极限约束条件下的轨迹优化问题，并采用Gauss伪谱法进行求解，将得到的外边界组成的多边形作为近似可达域[3]。文献[4]将再入可达域问题利用直接打靶法转化为四类情形的弹道优化问题，采用序列二次规划求解满足约束的再入可达域，文献[5]利用梯度修复算法求解轨迹优化问题，得到再入可达域。文献[6]在拟平衡滑翔条件下，将再入可达域计算问题转化为求解次优倾侧角控制律问题，进一步将其等价为虚拟目标逼近问题，并将过程约束转化为倾侧角约束，得到再入可达域。根据文献[7]在分析攻角优化问题的基础上，基于拟平衡滑翔条件结合飞行器再入多种约束，得到再入攻角的设计空间，给出再入攻角剖面设计方法，并应用于再入可达域优化。文献[8]利用拟平衡滑翔条件，通过零值倾侧角和最大横向航程生成虚拟目标集，将再入强约束条件转化为攻角下边界约束条件，得到飞行器再入可达域。文献[9]将可重复使用飞行器再入可达域转化为参数优化问题，针对该参数求解问题，结合全局和局部优化算法的特点，设计了遗传算法和模式搜索相结合的优化算法，获得满足过程约束和控制约束的再入可达域。文献[10]在加速度再入制导基础上，利用阻力加速度插值和倾侧角反转，快速估算再入可达域。文献[11]在能量-阻力空间里，将飞行器再入约束条件描述为阻力加速度边界曲线，在得到实际可用的上下边界后，利用插值计算得到阻力方案，从而生成再入可达区域。文献[12]在r-V空间通过设计“初始下降段、外边界跟踪段和终端调整段”三段设计的轨迹优化方法，沿走廊上沿获得最大纵向航程，而后通过平移边界跟踪段获得固定纵向航程下的最大横向航程，得到外边界，并沿走廊下边界获得内边界。文献[13]利用粒子群优化和倾侧角反转相结合的方法，设计参数化倾侧角剖面，实现可达域快速计算。文献[14]利用粒子群优化算法，结合倾侧角插值模型，实现再入可达域快速计算。

综上所述，现有的再入可达域计算问题本质上是复杂轨迹优化问题，并利用参数搜索方法求解。本文在此基础上，通过分析倾侧角剖面对航程的影响，将倾侧角剖面设计为3段或5段线性分段函数，利用差分进化算法，求解满足航程的倾侧角剖面。在得到对应最大横向航程倾侧角剖面和最大纵向航程倾侧角的基础上，设计倾侧角插值模型，生成倾侧角指令集，近似计算可达域。

1 问题描述

1.1 再入运动学方程

考虑地球自转的影响，建立高超声速飞行器的再入无量纲运动学方程[15]为：

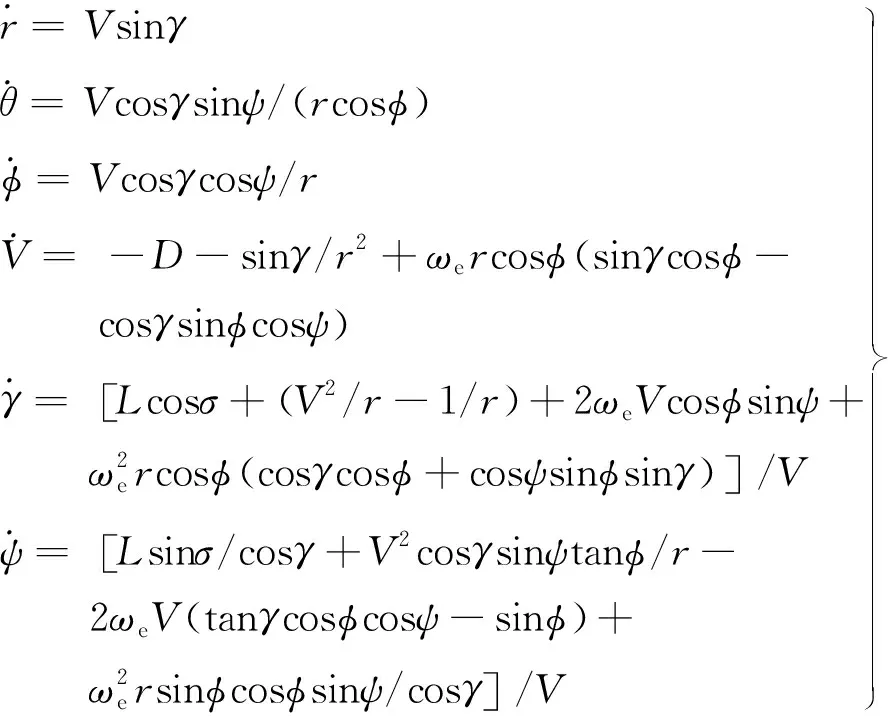
(1)

式中：r为无量纲地心距；V为飞行器无量纲飞行速度；θ和φ分别为经度和纬度；γ和ψ分别为飞行航迹角和航向角；ωe为地球自转角速度；σ为飞行器倾侧角；L和D分别为无量纲升力加速度和阻力加速度:

L=ρR0V2SrefCL/(2m)

D=ρR0V2SrefCD/(2m)

式中:R0为地球半径；Sref为飞行器参考面积；m为飞行器质量；CL和CD分别为升力系数和阻力系数；ρ为大气密度。

1.2 再入过程约束

Q=g0R0ρV2/2≤Qmax

(2)

(3)

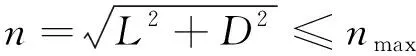
(4)

1.3 再入终端约束

为成功保证飞行任务，飞行器接近任务终端时，需要满足终端约束条件，通常包括[17]：

终端高度约束：

|hf-h|≤Δh

(5)

终端速度约束：

|Vf-V|≤ΔV

(6)

落点位置约束：

|θf-θ|≤Δθ，|φf-φ|≤Δφ

(7)

再入可达域主要采用外边界来表征，通常为扇形区域形式，如图1所示，E点是飞行器再入初始位置对应的星下点，EC为最大纵程，EA和EB为最大横程，外边界AC和BC由再入终端约束构成。

图1 再入可达区域示意Fig.1 Illustrations of reentry landing footprint

2 轨迹优化设计

高超声速飞行器再入轨迹一般由攻角和倾侧角确定。在大多数情况下，飞行器的攻角剖面根据飞行器过程的强约束条件，给定为速度的分段二次函数形式，如式(8)所示，飞行器再入航迹通过控制倾侧角实现。

(8)

式中：α0为初始再入攻角；VT为确定攻角曲线开始减小的临界速度；kα为常值系数，确定攻角下降速率。

2.1 倾侧角参数化再入轨迹设计

倾侧角剖面的幅值直接影响再入纵向航程，符号影响再入侧向航程。将倾侧角参数化为：

(9)

根据式(9)中σ1、σ2以及临界速度V2、V3取值不同，再入倾侧角剖面会具有不同的形式。当σ1和σ2同号时，倾侧角保持相同极性；当σ1和σ2符号相反时，倾侧角在[V4,V3]完成极性过渡。特别地，当V2=V3=(V1+V4)/2，σ1= (σ0+σ2)/2时，倾侧角5段分段函数则退化为3段，即：

在初始下降段，飞行器气动特性较弱，选取常值倾侧角σ0作为控制变量。接近终端区域能量管理时，为了保证飞行器平稳飞行，选取常值倾侧角σ2作为控制变量。在度过初始下降段后，倾侧角保持线性递增或递减规律飞行一段时间，而后保持常值倾侧角σ1，调整飞行器的再入横纵向飞行偏差，而后保持倾侧角以线性递增或递减规律飞行。采取这样的倾侧角剖面，可以实现航向角的精准调节。参数化倾侧角剖面如图2所示。

通过对倾侧角剖面的参数化设计，再入轨迹优化问题转化为参数优化问题，从而可用含有多约束的非线性优化方法直接求解，且待求解的未知参数仅包括(σ0,σ1,σ2,V1,V2,V3,V4)，从而减小参数优化搜索空间，提高计算效率。

图2 参数化倾侧角剖面Fig.2 Profile illustrations of parameterized bank angles

2.2 差分进化算法

差分进化算法于1997年由Storn和Price在遗传算法等进化思想的基础上提出，本质是一种多目标(连续变量)优化算法，用于求解多维空间中整体最优解。差分进化思想的来源是遗传算法，模拟遗传学中的杂交、变异、复制来设计遗传算子。不同之处在于遗传算法是根据适应度值来控制父代杂交，变异后产生的子代被选择的概率值，在最大化问题中适应值大的个体被选择的概率相应也会大一些。而差分进化算法变异向量是由父代差分向量生成，并与父代个体向量交叉生成新个体向量，直接与其父代个体进行选择。这种选择更接近实际且逼近效果也更好。

定义{x1,x2,…,xD}为待优化的D个未知参数，且满足:

基于差分进化算法，实现参数优化的流程为：

1)初始化种群。随机产生初始种群满足

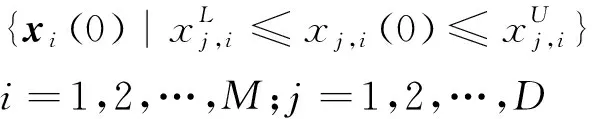
(10)

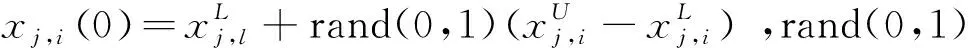
2)变异操作。通过差分策略实现种群个体变异，生成中间体，即：

vi(k+1)=xr1(k)+λ(xr2(k)-xr3(k))

(11)

式中：vi为变异操作生产的随机个体；r1，r2，r3为从第k代种群中随机选择的三个个体，i≠r1≠r2≠r3；λ为变异因子。

3)交叉操作。对第k代种群{xi(k)}及其随机个体{vi(k)}进行交叉操作：

(12)

式中：uj,i为通过概率方式生产的随机个体；cr为交叉概率；jrand为[1,2,…,D]的随机整数。

4)选择操作。通过贪婪算法选择进入下一代的种群个体：

xi(k+1)=

(13)

轨迹优化问题包含复杂的终端约束和过程约束，有效处理再入过程的等式和不等式约束是保证再入优化轨迹可行的关键。本文将这些约束条件以罚函数形式，添加到适应度函数中，为：

(14)

式中：ωm≥0(m=1,2,…,p)为罚函数权重；ϑm(x)为与优化参数x相关的等式约束。

对于不等式约束，包括动压约束式(2)、热流密度约束式(3)或过载约束式(4)，当这些强约束条件中的任一个超出给定的最大范围时，则将该个体对应的适应度函数J进行极大化，从而保证通过父本得到的新个体能够满足硬约束条件。

2.3 倾侧角插值模型

基于倾侧角插值模型的再入可达区域计算可归结为：1)求解两条具有最大横向航程的再入滑翔轨迹；2)将最大横向航程轨迹对应的倾侧角剖面指定为线性插值模型的基准剖面，并选取合适的插值模型系数，计算倾侧角插值剖面集合；3)将倾侧角剖面集合中的控制指令代入三自由度再入运动学模型，生成具有不同机动能力的再入轨迹集合，完成再入可达区域的近似计算。

设计倾侧角线性插值模型为：

σ(V)=σup(V)+η(σdown(V)-σup(V))

(15)

式中:σup(V)和σdown(V)分别为给定的基准倾侧角剖面;η∈[0, 1]表示倾侧角插值模型系数。

通过选取一定间隔的插值模型系数η(如η=0.2, 0.4, …, 0.8)，能够直接生成一组具有不同幅值和不同临界速度的倾侧角剖面集合,如图4所示，当倾侧角系数分别取η= 0和η= 1时，对应的倾侧角剖面即为插值模型式(15)的上边界σup(V)和下边界σdown(V)。

3 仿真分析

飞行器气动参数[19]可近似为：

CL=-0.234 2+0.051 36α+0.294 3e-0.100 7Ma

CD=0.024 67+0.000 714 3α2+0.325 2e-0.279 0Ma

给定再入攻角剖面为再入初始攻角α0= 30°，临界速度VT=4 500 m/s，kα=1.429 837 9×10-6，倾侧角取值范围约束为-60° ～ 60°，初始下降段选取常值倾侧角为σ0= 0°。

3.1 差分进化算法再入轨迹求解方案

给定5组不同的高超声速飞行器再入初始条件，如表1所示，并指定期望再入终端约束为hf=24 km，Vf=1 400 m/s，θf= 45°，φf= 30°。

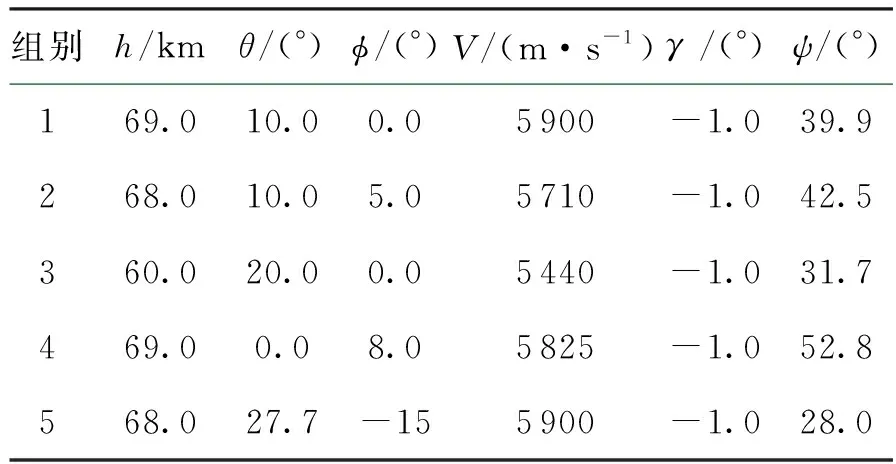
表1 飞行器再入初始条件

利用差分进化算法，针对表1中给出的初始条件，可求解满足终端约束、过程约束的倾侧角剖面，即参数：(σ0,σ1,σ2,V1,V2,V3,V4)。

图5给出了不同再入条件下飞行器的经纬度轨迹，5组仿真结果都满足预定的经纬度精度要求。图6给出了求解得到的倾侧角剖面。

由图6可见，组4和组5相较于组1～组3多进行了一次倾侧角反转，用于调整飞行器航向角。参数化的倾侧角剖面求解结果如表2所示。

图5 再入经纬度轨迹Fig.5 Reentry longitude and latitude trajectory

图6 再入倾侧角剖面Fig.6 Reentry bank angle profile

表2 参数化倾侧角剖面求解结果

3.2 再入可达域计算

考虑最大航向航程再入轨迹，选取性能指标为：

minJ=

并选取飞行器再入初始条件如表3所示，给定终端约束为hf= 24 km，Vf= 1 500 m/s。

表3 飞行器再入初始条件

线性插值模型参数η在区间[0, 1]上以0.1间隔依次取值，在得到飞行器最大横向航程的基础上，生成再入倾侧角指令集，如图7所示。

如图8所示,ηr= 1和ηl= 1分别对应了高超声速飞行器最大横向航程时的轨迹，且对应于图7中的ηr= 1和ηl= 1表示的倾侧角剖面。以η= 0和ηr= 1以及η= 0和ηl= 1分别构建出式(15)中的下边界σdown(V)和上边界σup(V)，根据η取值生成倾侧角插值剖面，将其代入飞行器运动学模型，可计算得到飞行器的再入可达域。