正推逆证思路在初中数学几何中的应用

杜会利

摘 要：随着新课标改革的不断推进，数学教学要求逐渐加深。数学在实际生活中应用比较广泛，初中数学教学具有十分重要的地位。初中数学中的几何题型贯穿整个教学阶段。但是由于其对学生的空间思维和逻辑分析能力要求较高，很多学生在进行学习的过程中并不能够很好地把握，就使得逐渐淡化了了学习的兴趣，造成数学科目整体的成绩较差。在本文中，笔者就凭借自己多年的初中数学教学经验，谈一谈正推逆证思路在初中数学几何中的应用。

关键词：正推逆证；初中数学；几何教学；应用

正推思路我们比较容易理解，就是根据题目中所提供的有效条件来对其进行相应的推理，最终得出问题答案的过程。而逆向思路都与大多数学生来说比较难以掌握和理解，其实逆向思路也叫做求异思维，就是对人们常生活中习以为常或者早已经成为定论的事物或者观点进行反向思考的一个思维过程，敢于对一个问题反其道而行之，从思维过程的对立面来对其进行相应的探索，树立起一个新思想，创立起一个新过程。

一、初中几何教学的实际现状

在初中教学的实际过程之中，几何教学一直是困扰着学生学习的重大阻碍，它不仅要求学生有着较强的数学计算能力，而且还对学生的空间想象能力有着较高要求，这样就会使得学生在具体的学习过程中显得十分的吃力。而且大多数老师对于几何教学的教学模式都是采取“填鸭式”的教学模式，老师在上面讲学生在下面被动的接受，不能够进行良好的师生互动，这样就使得学生自己对于知识内容的探索不能够更加的深入，时间长了就会慢慢丧失对于几何内容的学习兴趣。所以老师在进行几何内容的实际教学过程中，要特别注意知识的传授方式和学生对于知识的接受情况，采取合理的教学模式来满足学生对于知识的渴求，进而切实提高学生对于几何数学的学习能力。

二、借助几何图形，进行合理的猜想

在处理几何题目的过程之中，大多数题型是可以通过正推方法来进行解决的，因为很多题目的信息都蕴含在几何图形之中，比如长度、形状、位置等等。如果学生能够很好的发掘其中所蕴含的有效信息，并将其中的关系有效地串联起来，通过合理的猜想假设，就可以很好地找到解决题目的思路，来进行相关的证明解决。

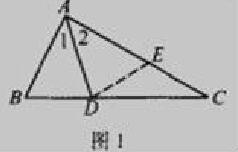
例：如图1所示。在△ABC中，∠B=2∠C，AD是∠A的角平分线。求证AB+BD=AC。对于这种题型来说，多采取正推法来解决。

如果在AC上截取AE=AB，这样就只需求证BD=EC即可，而结合AD是∠A的平分线，利用三角形全等的相关定理，以及三角形外角是内角的关系进行合理的猜想，就能够很轻松的得出解题思路。

证明 如图所示，在AC上截取AE=AB，

由于AD是∠A的角平分线，即∠1=∠2，

又因為AE=AB，AD为公共边，

所以根据全等定理，△BAD≌△EAD，

所以BD=DE，∠B=∠AED，

又因为∠AED=∠C+∠EDC，∠B=2∠C，

所以∠C=∠EDC，所以EC=ED

所以EC=BD，

所以AB+BD=AE+EC=AC

总结：在大多数的几何题目图形之中，题目之中或者图形内所蕴含的已知条件是很多的，虽然大部分已知条件看起来是没有关联的，所以这就需要学生们进行具体的思索，寻找它们之间的联系。

三、利用逆向思维模式，进行几何问题的相应解决

利用逆向思维的解题方式，将传统的解题思路颠倒过来，由未知问题去推导已知条件，这种新颖的解题方式能够给学生带来更多的学习兴趣，进而能够更加全身心地投入到几何问题的学习过程中。

在当今人教版的几何内容过程过程之中，首先引入的是学生比较熟悉的线段内容，在平行线之中要求学生进行一些简单的推理，利用逆向思维的推导方式，能够对于问题进行一个更好的解决。

例如，如图所示，在△ABC中，BE，CF分别是AC，AB两边上的高，在BE上截取BD=AC，在CF上的延长线上截取CG=AB，连接AD，AD。

求证：（1）AD=AG。

（2）AD与AG的关系如何。

分析：（1）要证AD=AG→△ABD≌△AGC→∠ABD=∠ACG→∠FHB=∠EHC→CF⊥AB（已知条件）；AB=GC（已知条件）；BE⊥AC（已知条件）；AG=AD（已知条件）。

（2）由（1）可知，∠AGC=∠BAD→∠AGC+∠GAF=90°→∠DAG=90°→AD⊥AG。

通过这种逆向思维的推理方法，学生对于几何问题的分析就会有着更好的理解，相应的在这种题型中就会花费更少的时间。而且这种逆向思维的推理模式不仅能够运用于几何题型之中，对于其他的数学问题也能够很好的解决，这样对于学生学习数学也是一个很好的帮助。

总而言之，在进行实际问题的解决过程中，也需要通过一些相应的逻辑思维模式来进行具体的解题步骤，所以这就要求老师在实际的教学过程中能够把握好几何推理过程的相应特点，进行相应思维模式的讲解，从而使得学生能够更好地掌握这些内容的知识点，完成实际的教学目标。

参考文献：

[1]范成.初中数学几何推理与图形证明策略例谈[J].数理化解题研究（初中版），2014（10）.

[2]胡敏华.浅析逆向思维在初中数学中的应用[J].读书文摘，2014，03.