纵向涡发生器排数对三维喷动床内气-固两相流动影响数值模拟

张洁洁, 尚灵祎, 吴 峰, 马晓迅,2, 杨 剑

(1.西北大学 化工学院， 陕西 西安 710069； 2.陕西省洁净煤转化工程技术中心， 陕西 西安 710069； 3.西安交通大学 能源与动力工程学院， 陕西 西安 710049)

喷动床作为一种高效反应处理器广泛应用于颗粒粉碎、颗粒干燥、化学反应、涂层热解等领域[1-4]。目前，很多研究者致力于几种结构固定的传统喷动床的研究，但传统喷动床内环隙区颗粒体积分数较大，颗粒缺少横向运动，严重影响了作为主要反应区域的环隙区处理物料的效率[1]。针对传统喷动床的以上不足，笔者提出了一种新型的带纵向涡发生器喷动床来改善床内多相传递过程，气体经由纵向涡发生器产生纵向涡流，从而强化喷动床内环隙区与喷射区间颗粒、气体的横向混合。参照He等[5-6]研究的喷动床整体结构参数，并以此实验数据作为数值模拟工作的校核标准，在三维喷动床内加入了纵向涡发生器(球体扰流件)，采用Fluent15.0软件对带纵向涡发生器喷动床内的气-固两相流动特性进行了数值模拟，研究纵向涡发生器及纵向涡发生器排数对三维喷动床内气-固两相流动的影响规律，并对其进行模拟优化。

1 数学模型

采用拟流体模型将离散颗粒相处理为具有连续性的流体，颗粒相与连续相守恒控制方程形式相同，模拟计算过程中质量守恒方程、动量守恒方程以及曳力模型与文献[7-8]一致。

2 模拟结果与讨论

为验证数值模拟模型的可靠性，通过数值模拟方法分析无扰流件三维喷动床并与文献[5-6]实验数据进行对比，数值模拟喷动床尺寸与文献的实验喷动床一致。以颗粒速度为分析对象，对计算模型进行网格无关性分析，计算网格数分别设定为165600、235481、340300、452452和549721。文中床高起点为喷动床进口处，图1为在床高z=0.218 m处，不同网格数下轴中心的最大颗粒速度(vs, max，m/s)随网格数的变化。计算表明，数值模拟的精度随网格数的增加而提升，当网格数大于452452时，数值模拟结果达到了网格无关性的要求，笔者将此网格划分密度进一步应用于带纵向涡发生器喷动床。无扰流件三维喷动床内颗粒速度的模拟值与文献实验值对比如图2所示，由图2可知，颗粒速度的模拟值与实验值变化趋势一致，最大偏差在22%以内，表明所采用喷动床的数值模型具有一定的合理性。笔者将采用此数值模型对单排及多排纵向涡发生器三维喷动床内气-固两相流动规律进行模拟及优化分析。

图1 网格无关性Fig.1 Grid independencyz=0.218 m

图2 不同床高下颗粒速度模拟值与实验值Fig.2 Particle velocity comparison of numerical simulation and experimental results at different spouted bed heights U=1.3Umsvs—Particle velocity; r—Radial distance; U—Inlet gas velocity; Ums—Minimum gas inlet velocityz=0.168 m(Experiment); z=0.168 m(Simulation); z=0.218 m(Experiment); z=0.218 m(Simulation); z=0.268 m(Experiment); z=0.268 m(Simulation)

图3为喷动床与纵向涡发生器的网格示意图。纵向涡发生器结构选为球体，喷动床内纵向涡发生器区域的网格类型为非结构化网格，其余区域为结构化网格。数值模拟中气体、颗粒两相物性值的选择参见文献[5-6]，其中气体密度(ρg)为 1.225 kg/m3，颗粒密度(ρs)为2503 kg/m3，气体黏度(μg)为1.7894×10-5Pa·s，颗粒直径(ds)为1.41 mm，颗粒体积分数(φs)为0.588, 喷动床的固定床高(H0)为325 mm，喷动床直径(D)为152 mm,最小表观气速(ums)为0.54 m/s，最小气体入口速度(Ums)为34.56 m/s，模拟采用的实际入口气速为1.6Ums，喷动床的总床高度(z)为0.700 m。纵向涡发生器的小球半径为10 mm，同排小球径向球心距为30 mm，相邻两排小球轴向球心距为30 mm。采用双流体模型(TFM)处理气-固两相传递过程[8]，其中气相采用标准k-w湍流模型描述[9]，颗粒相采用颗粒动力学理论模型处理[10]，气-固相间作用力采用Gidapow曳力模型[10-11]；采用SIMPLE耦合算法计算压力-速度方程[12]，对于湍流方程、动量方程采用二阶迎风离散格式，固相体积分数采用一阶迎风离散格式进行计算。计算时间步长为0.00002 s，计算残差小于10-3，恢复系数取值为0.8。气体入口设置为湍流速度分布，其表观气速u=0.864 m/s，喷动床的进口气速方向垂直于入口边界，其湍流强度值设置为3%，黏性率设置为0.0019。喷动床气体出口为Outflow边界，气体和颗粒相在壁面处均为零滑移剪切应力边界条件。

图3 喷动床与纵向涡发生器的网格示意图Fig.3 Grid diagram of spouted bed with longitudinal vortex generators(a) One pair of sphere; (b) Two pairs of sphere; (c) Three pairs of sphere

2.1 颗粒体积分数分布

通过数值模拟方法重点研究纵向涡流对喷动床内颗粒体积分数径向分布的影响，当计算时间为t=4 s时，喷动床内气-固两相流动基本达到稳定状态，喷动床内呈现明显的喷射区、环隙区及喷泉区结构。流动参数时均值的计算样本取4～6 s时间段，时间间隔为0.5 s。图4为喷动床内颗粒体积分数分布云图。由图4可知，纵向涡发生器的加入显著增加了气体、颗粒在喷动床内向上运动的阻力，从而降低了喷泉高度。且随着纵向涡发生器排数的增加，颗粒的动能损失越多，颗粒的喷泉高度逐渐降低。

图4 喷动床内颗粒体积分数分布云图Fig.4 Particle volume fraction distribution cloud maps in spouted bedsφ—Particle volume fraction(a) No sphere; (b)One pair of sphere; (c)Two pairs of sphere; (d)Three pairs of sphere

图5为不同喷动床在相同床层高度下颗粒体积分数(φ)的分布。由图5可知，纵向涡流能够有效影响喷动床内颗粒体积分数的径向分布规律，提升了近喷射区域内颗粒的体积分数，使得颗粒沿径向分布更加均匀。在低床层高度区域(z=0.170 m)，此区域距离纵向涡流影响区域较远，纵向涡发生器排数对颗粒体积分数分布的影响很小。随着床层高度的逐渐增加，分析区域逐渐进入了纵向涡流的影响范围，纵向涡流的影响效果逐渐明显，近喷射区颗粒体积分数随纵向涡发生器排数的增加显现先上升后下降的非线性趋势，表明在喷动床的有限空间内，纵向涡发生器排数设计及对颗粒径向运动的影响能力受到了空间的限制。研究表明，在纵向涡流的影响区域，2排纵向涡发生器能够使喷动床内整体颗粒体积分数沿径向分布实现最均匀状态，即对喷动床内颗粒径向运动的强化效果达到最佳。

2.2 颗粒速度

图6为喷动床横截面内颗粒速度分布云图。由图6可知，加入纵向涡发生器，颗粒在导流板两侧产生了二次纵向涡流，二次涡流的出现能够有效地强化喷动床内喷射区和环隙区内颗粒的径向混合，进而增强了喷动床内整体气体、颗粒两相间的动量交换。

图7为不同喷动床在相同床层高度下颗粒径向速度(vr)的分布。由图7可知，纵向涡流能够有效增加喷动床内颗粒的径向速度，从而强化颗粒的径向运动能力，当床层高度较低时(z=0.170 m)，多排纵向涡发生器及其产生的纵向涡流对颗粒径向速度的影响强度要高于单排纵向涡发生器。随着床层高度的增加，纵向涡发生器排数对喷射区内颗粒径向速度的影响逐渐降低，而对环隙区内颗粒径向速度的影响逐渐增强(z=0.230 m)。

图5 不同喷动床在相同床层高度下颗粒体积分数(φ)的分布Fig.5 Comparison of particle volume fraction(φ) distribution in spouted beds at the same bed heightU=1.6Ums(a) z=0.170 m; (b) z=0.200 m; (c) z=0.230 m━No sphere; One pair of sphere; Two pairs of sphere; Three pairs of sphere

2.3 颗粒拟温度

图8给出了在不同纵向涡发生器排数的影响下，不同床高处颗粒拟温度沿喷动床径向距离的变化曲线。由图8可知，喷射区内颗粒拟温度随着床层高度的增加而逐渐降低，且带纵向发生器的喷动床内颗粒拟温度的下降速率较无扰流件的更快。在低床层高度处(z=0.170 m)，气体纵向涡流强化了颗粒的径向运动，一定程度上增加了颗粒拟温度；另一方面，随着床层高度的增加，颗粒运动进入了纵向涡流的核心影响区域，喷射区与环隙区内的气体、颗粒在纵向涡流影响下发生了强烈的径向混合，有效地消耗了颗粒群的运动动能，从而降低了该区域的颗粒拟温度，使得颗粒拟温度随床层高度的增加而迅速降低，甚至出现了低于无扰流件喷动床内颗粒拟温度的情况(见图8(c))。

3 结 论

(1) 纵向涡发生器的加入显著增加了气体、颗粒在喷动床内的运动阻力，从而降低了喷泉高度。且随着纵向涡发生器排数的增加，颗粒的喷泉高度逐渐降低。

(2) 纵向涡流能够显著改变喷动床内颗粒体积分数的径向分布规律，有效地提升近喷射区域颗粒体积分数，使得颗粒沿径向分布更加均匀。在纵向涡流充分影响区域内，2排纵向涡发生器对喷动床内颗粒径向运动速度的强化效果达到最佳。

(3) 纵向涡流能够有效增加喷动床内颗粒的径向速度值，强化了颗粒的径向运动能力。多排纵向涡发生器及其产生的纵向涡流影响强度要高于单排纵向涡发生器。随着床层高度的增加，纵向涡发生器排数对喷射区内颗粒径向速度的影响能力逐渐降低，而对环隙区及近环隙区内颗粒径向速度的影响逐渐增强。

图6 喷动床横截面内颗粒速度分布云图Fig.6 Comparison of velocity contours of particle phase in cross section of spouted bedsz=0.170 m(a) No sphere; (b) One pair of sphere; (c) Two pairs of sphere; (d) Three pairs of sphere

图7 不同喷动床在相同床层高度下颗粒径向速度(vr)的分布Fig.7 Comparison of particles radial velocity (vr) distribution in spouted beds at the same bed heightU=1.6Ums(a) z=0.170 m; (b) z=0.200 m; (c) z=0.230 m━No sphere; One pair of sphere; Two pairs of sphere; Three pairs of sphere

(4) 在纵向涡流效应的影响下，喷动床喷射区内的颗粒拟温度值随着床层高度的增加而逐渐降低，气体、颗粒在纵向涡流的影响下发生了强烈的径向混合，消耗了颗粒群的运动动能，使得颗粒拟温度值随床层高度的增加而迅速降低。

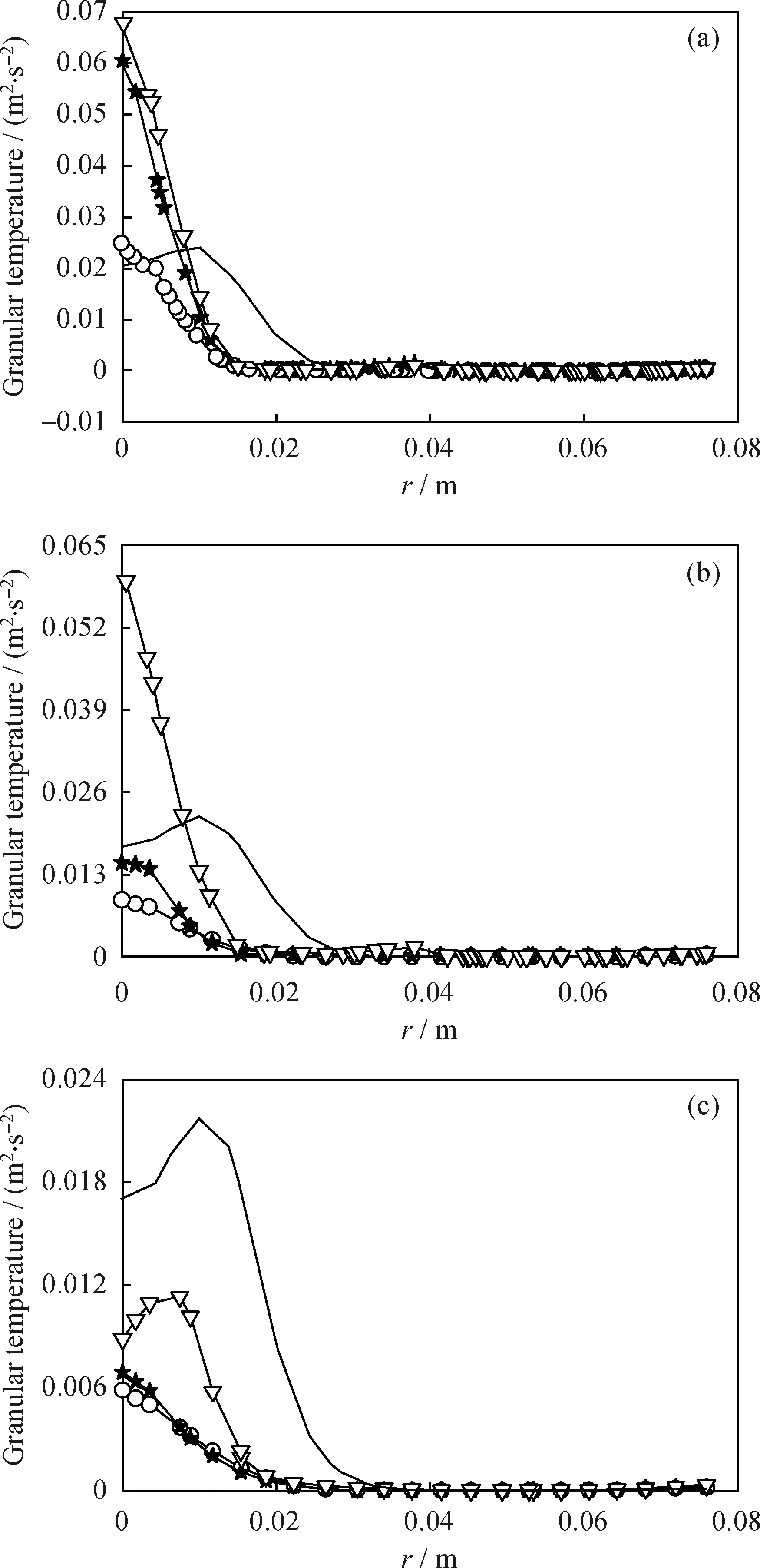
图8 不同喷动床在相同床层高度下颗粒拟温度的分布Fig.8 Comparison of granular temperature profile along radial and axis in spouted beds at the same bed heightU=1.6Ums(a)z=0.170 m; (b)z=0.200 m; (c)z=0.230 m━No sphere; One pair of sphere; Two pairs of sphere; Three pairs of sphere

[1] 金涌, 祝京旭, 汪展文. 流态化工程原理[M]. 北京：清华大学出版社, 2001.

[2] 祝京旭, 洪江. 喷动床发展与现状[J]. 化学反应工程与工艺. 1997, 13 (2): 207-230.(ZHU Jingxu, HONG Jiang. Development and present situation of spouted bed [J]. Chemical Reaction Engineering and Technology, 1997, 13(2): 207-230.)

[3] 张少峰, 李玲密, 王晋刚. 喷动床半干式烟气脱硫脱硝实验研究[J]. 环境工程学报, 2011, 5(8): 1847-1851.(ZHANG Shaofeng, LI Lingmi, WANG Jingang, et al. Experimental research of semi-dry flue gas simultaneous desulfurization and denitrification with spouted bed[J]. Chinese Journal of Environmental Engineering, 2011, 5(8): 1847-1851.

[4] BANERJEE S, AGARWAL R. Transient reacting flow simulation of spouted fluidized bed for coal-direct chemical looping combustion with different Fe-based oxygen carriers[J]. Applied Energy, 2015, 160(2):552-560.

[5] HE Y L, QIN S Z, LIM C J, et al. Particle velocity profiles and solid flow patterns in spouted beds[J]. Canadian Journal of Chemical Engineering, 1994, 72(4): 561-568.

[6] HE Y L, LIM C J, GRACE J R, et al. Measurements of voidage profiles in spouted beds[J]. Canadian Journal of Chemical Engineering, 1994, 72(2): 229-234.

[7] 黄明辉, 马晓迅, 宋一鸣,等. 喷动床内气固二相流动行为的计算模拟[J]. 化学工程, 2010, 38(2): 31-35.(HUANG Minghui, MA Xiaoxun, SONG Yiming, et al. Calculational simulation of gas-solid flow behavior in spouted bed[J]. Chemical Engineering (China), 2010, 38(2): 31-35.)

[8] WANG S Y, ZHAO L Q, WANG C S, et al. Numerical simulation of gas-solid flow with two fluid model in a spouted-fluid bed [J]. Particuology, 2014, 14(3):109-116.

[9] WILCOX D C. Reassessment of the scale-determining equation for advanced turbulence model[J]. AIAA Jouranl, 1988, 26 (11) :1299-1310.

[10] DING J, GIDASPOW D. A bubbling fluidization model using kinetic theory of granular flow[J]. AIChE Journal, 1990, 36(4): 523-538.

[11] DENG Z, XIAO R, JIN B, et al. Computational fluid dynamics modeling of coal gasification in a pressurized spout-fluid bed[J]. Energy & Fuels, 2008, 22(3): 1560-1569.

[12] PATANKAR S V, SPALDING D B. A calculation procedure for heat, mass and momentum transfer in three dimensional parabolic flows [J]. International of Heat and Mass Transfer, 1972, 15(10): 1787-1806.