催化裂化烟气轮机内不同Stokes数颗粒沉积特性数值研究

2018-10-10潘静娜王建军陈帅甫徐书根

石油学报（石油加工） 2018年5期

潘静娜，王建军，陈帅甫，徐书根

(中国石油大学(华东) 化学工程学院，山东青岛 266580)

催化裂化装置能耗占炼油厂总能耗的25%左右，在各装置能耗中居第一位。烟气轮机(简称烟机)是催化裂化装置中的主要能量回收设备[1]，其主要作用是回收再生烟气的热能及压力势能，带动主风机发电。在能量回收系统中，余热锅炉中的气速约为2～10 m/s，旋风分离器中的气速约为40～80 m/s，而在烟气轮机中气速可达400～600 m/s，根据颗粒与壁面的相对运动速度大小可以将能量回收系统中的设备分为低滑移速度设备和高滑移速度设备[2]。高滑移速度设备长期在恶劣的环境下运行，转速高达6000～7000 r/min，高温烟气中还含有多种腐蚀性成分及催化剂颗粒，这些因素都会造成烟机效率下降、振动异常甚至叶片断裂，从而导致烟机非正常停工[3-4]。

为了保证烟机安全运行，避免因结垢造成烟机故障，国内外学者对烟气轮机内气-固两相宏观流动进行了较多的数值研究，但大多数是研究颗粒运动轨迹、叶片磨损及结垢机理[5-8]，较少涉及颗粒在壁面的沉积黏附情况。催化剂颗粒在烟气轮机流道内运动情况复杂，不同Stokes数颗粒的运动轨迹不同[9]，颗粒在高温、高压及复杂气体环境中弹跳碰撞，极易沉积在叶片表面，造成叶片结垢。前人大多基于实验方法研究叶片结垢问题[10-11]，然而从经济性和时效性方面来看，数值模拟方法具有实验方法所不具备的优势。因此，笔者在前人实验研究的基础上，采用自定义函数的方法修正了Fluent中的固有沉积模型，模拟不同Stokes数颗粒在叶片表面沉积过程，探索改善叶片结垢的方法，为工业上烟气轮机阻垢技术的开发提供理论依据。

1 数值计算模型

1.1 湍流模型与离散相模型

图1为烟气轮机叶片结构示意图。烟气轮机属于高速旋转叶轮机械，其内部流线弯曲程度较大。

图1 烟气轮机叶片结构示意图Fig.1 Structure of flue gas turbine blades

相对于标准k-ε模型，RNGk-ε模型[12]通过修正湍流黏性系数来模拟平均运动中的有旋流动，能够较为准确地模拟烟气轮机内部流场，因此选用RNGk-ε模型为湍流模型。离散相模型(Discrete phase model，DPM)能够追踪颗粒的运动轨迹，且烟气轮机入口颗粒体积分数较低，因此采用DPM模型[13]为离散相模型。

1.2 修正的沉积模型

Fluent固有的沉积模型认为，颗粒碰壁即沉积导致计算结果偏离实际情况。为此笔者引入了颗粒与壁面碰撞的临界结垢应力，当颗粒与壁面的接触应力σjc大于临界结垢应力σs时，颗粒材料发生切应力破坏，认为其黏附在壁面。Maugis等[14]研究表明，两个互相接触物体间存在表面黏连力，显著影响由塑性变形引起的接触区域应力分布。同时，Johnson等[15]应用Griffith能量方法得到颗粒在外载荷与表面黏连力共同作用下的等效载荷P1，如式(1)所示。

(1)

表面黏连力直接影响计算结果的准确性，因此笔者在前人关于颗粒-壁面体系表面黏连力研究[14-15]的基础上，利用JKR接触理论[15]计算颗粒与壁面接触面半径a，如式(2)所示。

(2)

然后计算颗粒与壁面碰撞时产生的接触应力σjc，如式(3)所示。

(3)

颗粒临界结垢应力选取赵庆国等[16]催化剂颗粒压碎实验的平均测量值σs=75.010×106Pa。将以上沉积模型通过Fluent中的用户自定义函数(UDF)修正，并用于烟气轮机内催化剂颗粒沉积过程的数值模拟。

2 沉积模拟计算条件

2.1 计算区域及边界条件

实际烟气轮机静叶38片、动叶57片，由于烟气轮机模型及其内部流场具有周期性重复的特点，按照动叶、静叶数量为3/2的比例建立计算模型并划分网格，如图2所示。计算流场两侧设置为周期性边界条件，静叶入口设置为压力入口边界条件，动叶出口设置为压力出口边界条件，静叶和动叶流道内的数据通过交界面interface传递，轮毂、机壳及叶片的吸力面和压力面设置为壁面边界条件，转子转速为6100 r/min。

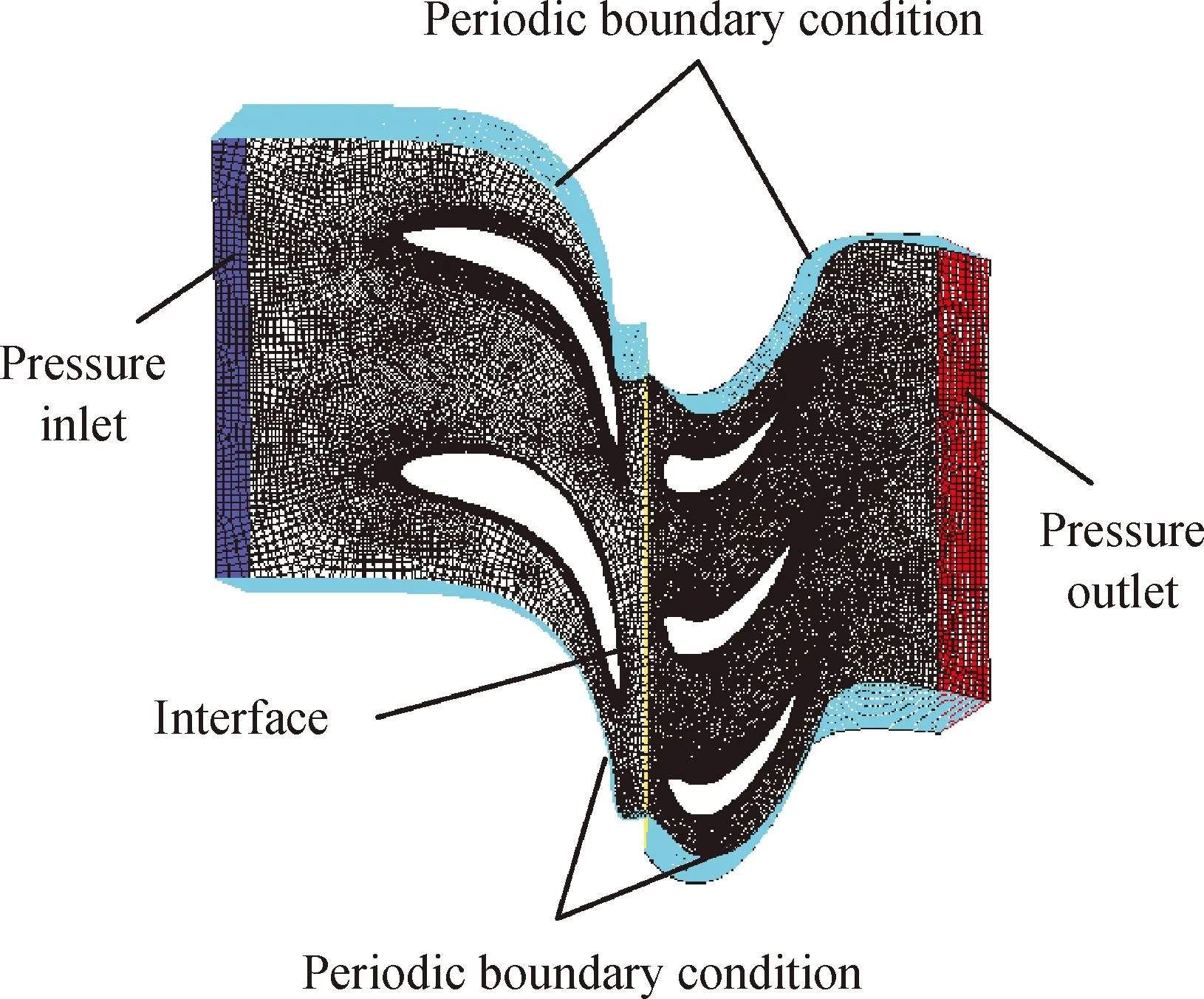
图2 计算区域网格划分反边界条件Fig.2 Mesh distribution and boundary condition of computational domain

2.2 研究对象

高温烟气被视为可压缩气体，其中N2、O2、CO2、SO2和水蒸气的体积分数分别为：74%、2.76%、13.72%、0.01%和9.51%。烟气轮机入口催化剂颗粒的粒径分布如图3所示，颗粒总质量流量为0.236 g/s。颗粒的密度和粒径共同决定Stokes数的大小，Stokes数定义为颗粒松弛时间与流体特征时间的比值。计算过程中将颗粒按粒径大小分为6组：<1 μm、1～3 μm、3～5 μm、5～7 μm、7～10 μm、>10 μm，对这6组颗粒的沉积特性进行对比分析。相应的Stokes数通过经验公式(式(4))计算得到，分别为<3×10-4、3×10-4～3.7×10-3、3.7×10-3～1.03×10-2、1.03×10-2～2.01×10-2、2.01×10-2～4.08×10-2、>4.08×10-2。

(4)

图3 烟气轮机入口催化剂颗粒粒径(dp)分布曲线Fig.3 Flue gas turbine inlet particle sizes(dp)

3 数值模拟结果及分析

3.1 模型验证

为了验证数值模拟的准确性，将气相模拟的速率分布与王建军等[17]PIV实验数据进行比较，结果如图4所示。烟气平均速率与入口平均速率之比定义为无量纲速率V，相邻2个叶片间中心面与中径截面相交于子午线，子午线上任意一点距入口的长度与子午线总长度之比定义为无量纲子午线距离L。由图4可知，数值模拟与实验所得的气相流场速度吻合较好。

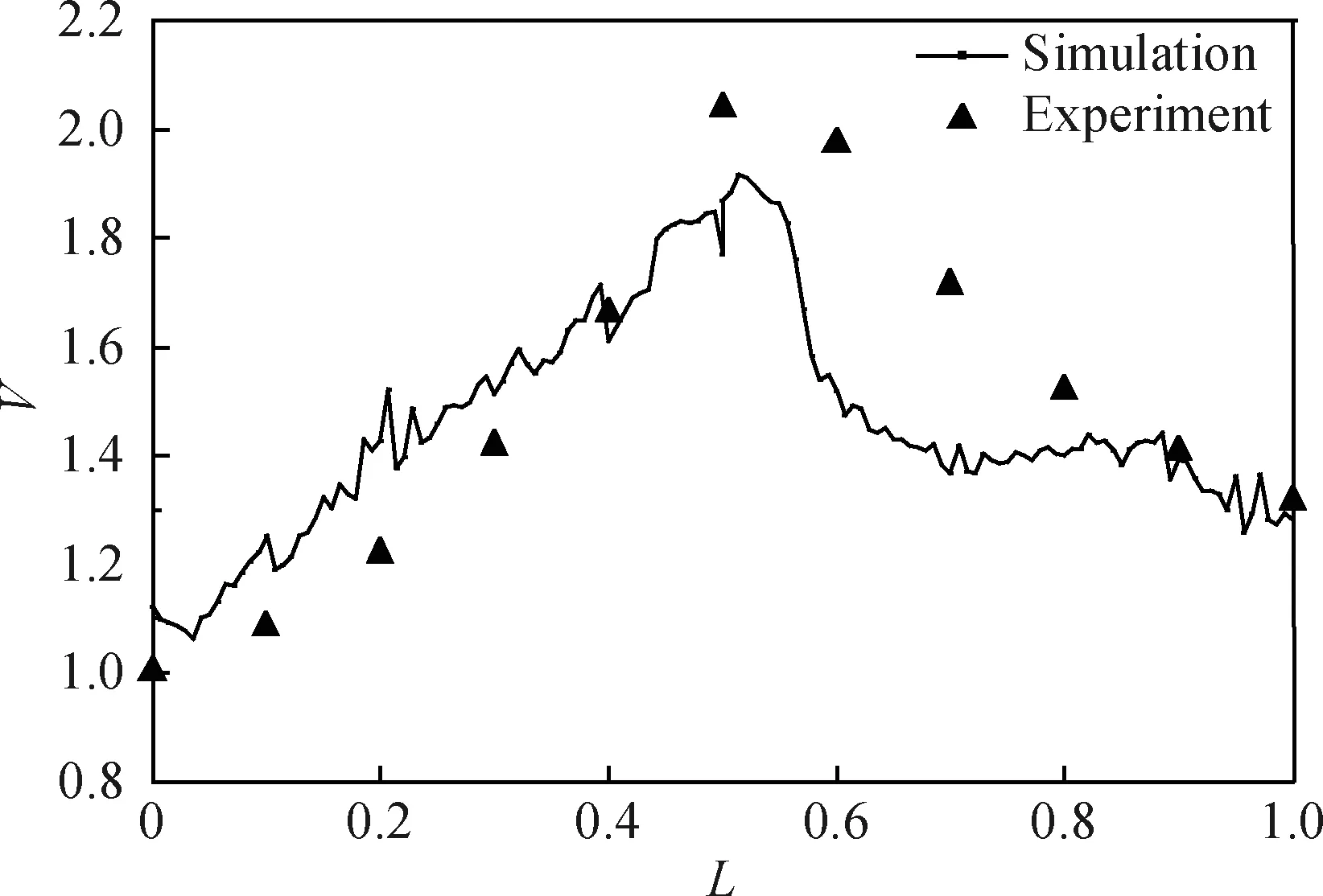
图4 烟气无量纲速率(V)随子午线距离(L)的变化Fig.4 Variation of dimensionless gas velocity(V) with dimensionless meridional distance(L)

3.2 气相结果分析

3.2.1 中径截面处的气相流场

图5为烟气轮机中径截面处的烟气压力分布云图。图6为中径截面处的烟气马赫数(Ma)分布云图。由图5可知，高温烟气在进入静叶入口时，静叶的叶尖处存在明显的高压区，压力沿烟气流动方向逐渐减小，静叶和动叶交界面处压力梯度骤然增大，造成烟气流动的不均匀性，加剧催化剂颗粒对叶片的冲刷；静叶吸力面后1/4处和动叶叶尖附近均存在明显的低压区，结合图5和图6可知，低压区的马赫数均大于1，不能忽略烟气的压缩性影响，与可压缩气体的设置吻合。

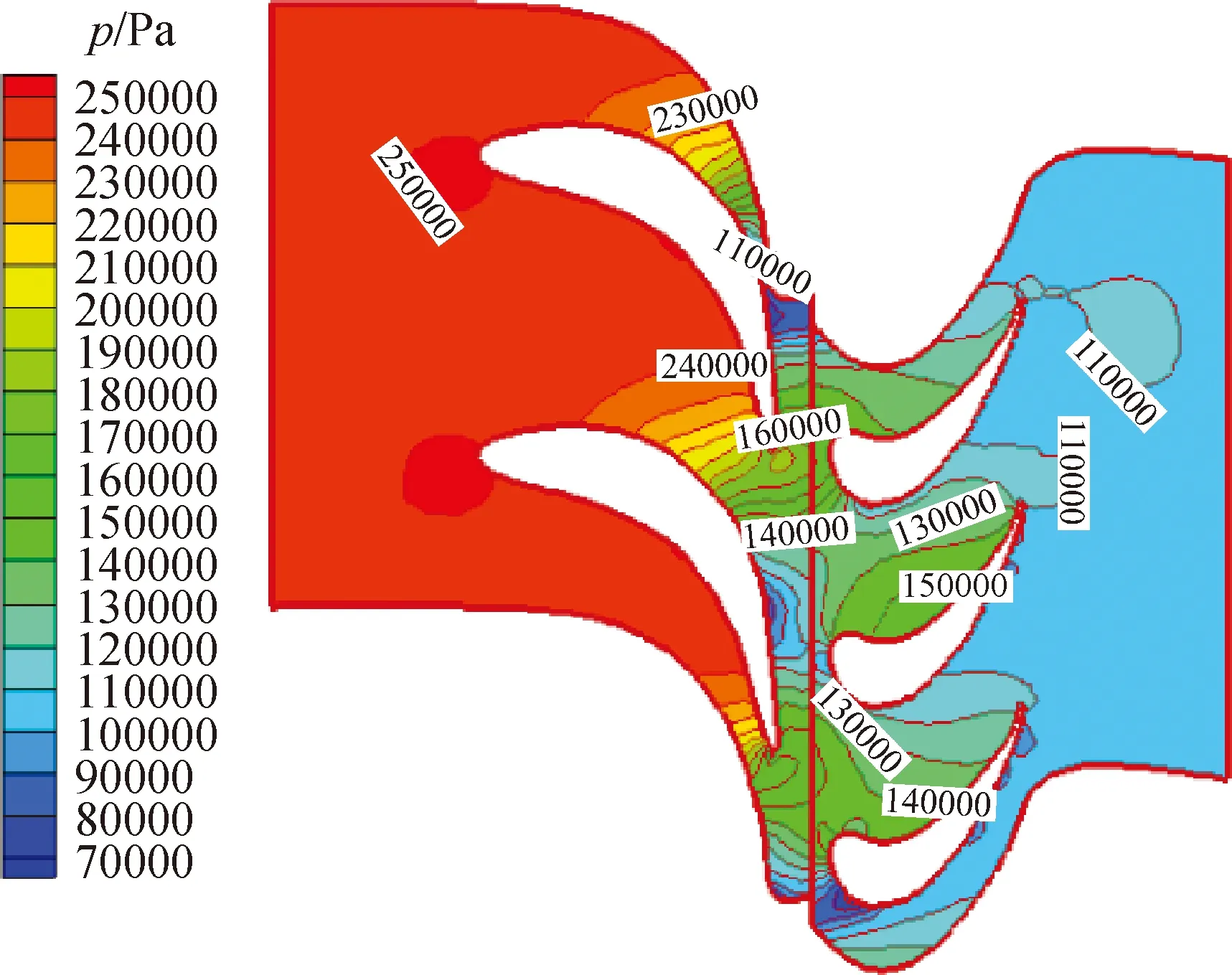
图5 中径截面的烟气压力(p)分布云图Fig.5 Flue gas pressure(p) of the middle section

图6 中径截面的烟气马赫数(Ma)分布云图Fig.6 Flue gas mach number(Ma) of the middle section

图7为烟气轮机中径截面处的烟气温度分布云图。由图7可知，烟气温度在入口处超过920K，并且沿着烟气流动方向逐渐降低，在静叶和动叶交界面处温度梯度较大，在静叶的叶尾处存在小范围高温区。谭争国等[18]研究发现，颗粒之间或颗粒与壁面之间在运动过程中发生碰撞、磨损，从而产生催化剂细粉，同时在催化裂化过程中加入平衡剂及原料油时引进的钙、铁、镍等金属附着在催化剂细粉表面，吸收烟气中的SOx和CO2，在923 K的气氛下焙烧，生成的低熔点共熔物是叶片结垢的主要成分。由图7还可知，叶片附近温度大致在840 K以上，因此颗粒会在此温度条件下形成低熔点共熔物，从而沉积在壁面。

图7 中径截面的烟气温度(T)分布云图Fig.7 Flue gas temperature(T) of the middle section

图8为烟气轮机中径截面处的烟气速率分布云图。由图8可知，静叶叶尖和动叶叶尾处均存在明显的低速区。由图5、图7和图8还可知，在静叶流道内，烟气的压力、温度沿流动方向逐渐降低，速率逐渐增大；在动叶流道内，烟气的压力、温度降低的幅度比静叶流道小，烟气流速也开始逐渐减小。

图8 中径截面的烟气速率(v)分布云图Fig.8 Flue gas velocity(v) of the middle section

3.2.2 叶片近壁面处的气相流场

图9为静叶片近壁面处的烟气温度分布云图(上边缘为机壳面，下边缘为轮毂面，下同)。由图9可知，吸力面附近温度梯度沿烟气流动方向变化较为明显，最低温度约为894 K；压力面附近温度分布相对较均匀，壁面平均温度约为926 K。

图10为动叶片近壁面处的烟气温度分布云图。由图10可知，动叶片近壁面温度梯度沿叶展方向变化极为明显。图11为动叶片近壁面处气相流线示意图。由图11可知，动叶片压力面和吸力面前缘均出现明显的二次流现象：在吸力面前缘，静叶流道出口处的烟气与从动叶出口回流的烟气相遇，气流由叶片机壳侧向轮毂侧流动，流动跟随性较强的颗粒容易被携带至叶片轮毂附近，为颗粒在此处的沉积提供条件；动叶片压力面前缘存在两处二次流，造成气体扰动，携带的颗粒在运动过程中不断改变运动方向，导致停留时间延长，增大沉积概率。

图9 静叶片近壁面处的烟气温度(T)分布云图Fig.9 Flue gas temperature(T) of the vane

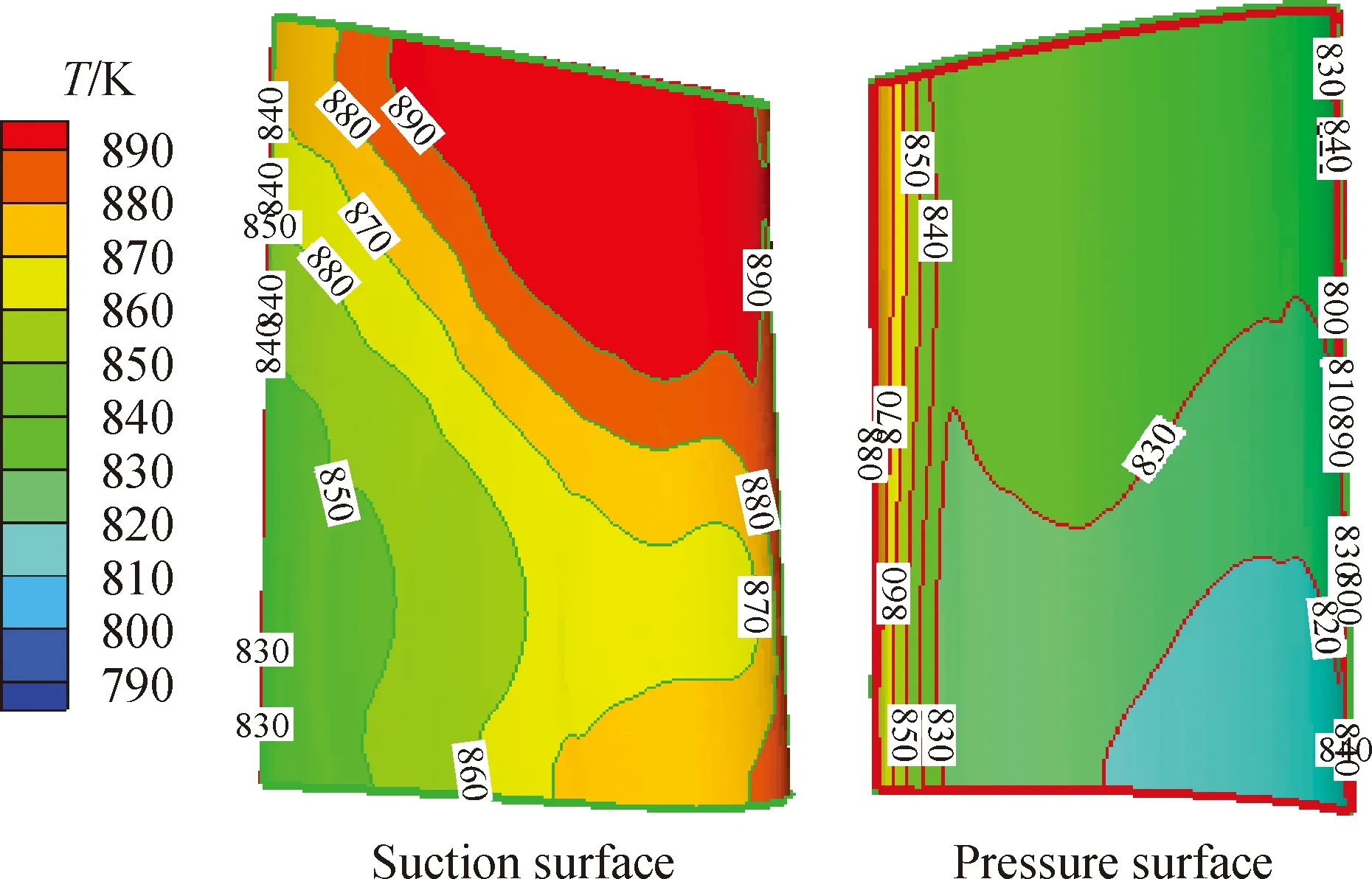
图10 动叶片近壁面处的烟气温度(T)分布云图Fig.10 Flue gas temperature(T) of the blade

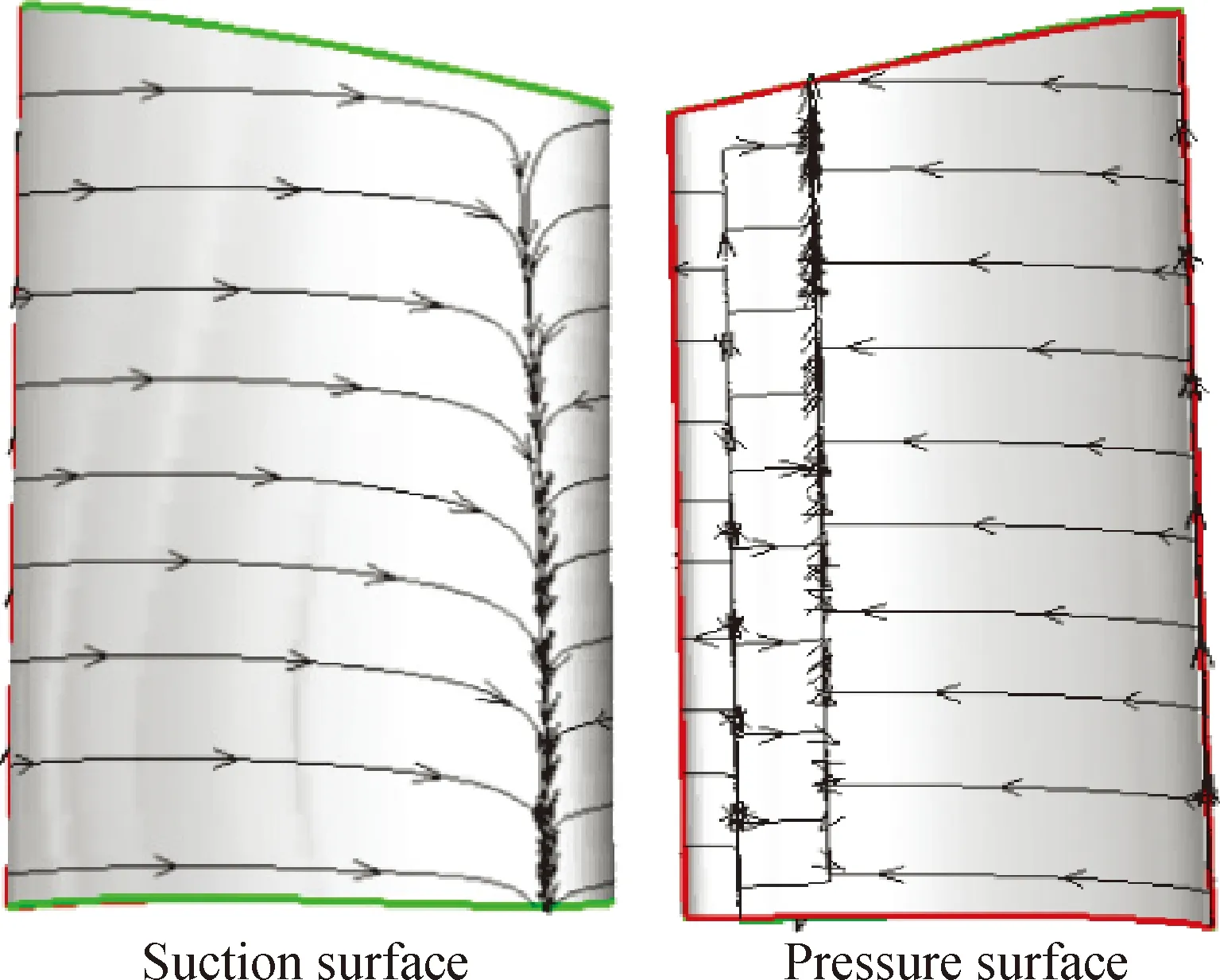
图11 动叶片近壁面处的气相流线示意图Fig.11 Streamlines of the blade

3.3 固相结果分析

3.3.1 静叶表面颗粒沉积情况

在气相流场模拟的基础上，将连续相与颗粒离散相耦合，以6组不同Stokes数的颗粒为研究对象，计算颗粒在叶片表面的沉积速率(q)。图12为静叶表面不同Stokes数催化剂颗粒的沉积速率分布云图。由图12可知，静叶表面沉积区域主要集中在吸力面，压力面几乎没有催化剂颗粒沉积。静叶表面沉积区域分布的差异性是由于静叶吸力面近壁面处烟气的温度梯度较大，颗粒在热泳力的作用下向吸力面移动，导致吸力面附近的颗粒浓度升高，沉积概率随之增大。

由图12(a)和图12(b)可知，Stokes数小于3.7×10-3的颗粒在静叶片吸力面的沉积速率明显超过压力面，吸力面的最大沉积速率约为26 μg/s，且随着Stokes数的增大，吸力面沉积区域由腹部向叶尖和叶尾处偏移。由图12(c)～图12(f)可知，Stokes数大于3.7×10-3的颗粒在压力面沉积区域的分布比较均匀，但沉积速率比Stokes数小于3.7×10-3的颗粒沉积速率低1～9个数量级。不同Stokes数颗粒之间沉积速率偏差产生的原因是，当颗粒的Stokes数较小时，流动跟随性较强，颗粒受到湍流扩散的影响相对于惯性作用明显，再加上热泳力对颗粒的迁移作用，这些因素均促使小Stokes数颗粒在吸力面上加速沉积；而大Stokes数颗粒与壁面碰撞时，其接触区域的半径增大，导致接触应力小于临界结垢引力，难以沉积在壁面，但颗粒本身具有的惯性使其更容易冲蚀磨损壁面。

3.3.2 动叶表面颗粒沉积情况

图13为不同Stokes数颗粒在动叶片的沉积速率分布。由图13可知，沉积区域主要集中在动叶吸力面轮毂、机壳附近以及整个压力面，这与动叶表面气相流场相吻合。由于动叶吸力面附近的烟气从机壳侧流向轮毂侧，并且烟气温度沿叶展方向逐渐升高，颗粒在热泳力和气相夹带的作用下迁移到轮毂侧，增大了颗粒在轮毂侧的沉积概率；吸力面机壳侧的颗粒同时受到二次流和惯性的影响，运动速度方向稍有偏移或保持不变，从而导致吸力面机壳侧及吸力面前缘近壁面处的颗粒浓度升高，为颗粒的沉积提供物质条件。动叶压力面存在两处二次流，气相流场紊乱，颗粒受紊流影响做不规则运动，不断与压力面碰撞、反弹，因此沉积区域几乎遍布整个压力面。

图12 不同Stokes数颗粒在静叶片的沉积速率(q)分布Fig.12 Deposition rate(q) of particles with different Stokes numbers on vanes(a) St<3×10-4; (b) 3×10-4≤St<3.7×10-3; (c) 3.7×10-3≤St<1.03×10-2; (d) 1.03×10-2 ≤St<2.01×10-2; (e) 2.01×10-2≤St<4.08×10-2; (f) St≥4.08×10-2

由图12和图13可知，动叶表面不同Stokes数颗粒的沉积速率与静叶表面对应颗粒的沉积速率具有相同的数量级，并且随着颗粒Stokes数的增大，沉积区域逐渐向吸力面腹部偏移，而压力面的沉积区域范围不断缩小。

4 结论

(1)通过自定义函数对Fluent固有的沉积模型进行修正，改进的沉积模型在考虑颗粒与壁面的表面黏连力作用的基础上，预测烟气轮机内颗粒的沉积规律。

(2)将连续相与不同Stokes数颗粒离散相耦合计算，结果表明，叶片表面的沉积速率与沉积区域受到颗粒Stokes数和气相流场的影响。具体表现为：烟气的温度梯度和湍流扩散作用会加速颗粒的沉积；随着颗粒Stokes数的增大，沉积速率逐渐减小，动叶吸力面沉积区域由轮毂、机壳附近向腹部偏移，动叶压力面、静叶吸力面沉积范围缩小，静叶压力面沉积范围增大。

(3)小Stokes数颗粒加速烟气轮机叶片结垢，破坏烟气轮机的安全长周期运行，因此工业应用时应尽量增大颗粒的Stokes数。主要有以下2种方法：通过工艺手段使催化剂细粉团聚，增大颗粒粒径；优化设计烟气轮机导流锥，使小Stokes数颗粒在到达静叶入口之前就从烟气中分离出来，从而减少叶片表面的结垢。

符号说明：

a——颗粒与壁面接触面半径，m；

dp——颗粒粒径，μm；

E*——颗粒与壁面的复合弹性模量，Pa；

L——子午线距离；

Ma——烟气马赫数；

p——烟气压力，Pa；

P——颗粒与壁面的冲击力，N；

P1——颗粒在外载荷与表面黏连力共同作用下的等效载荷，N；

q——颗粒的沉积速率，μg/s；

R*——颗粒与壁面的复合半径，m；