基于生存资料的II/III期无缝设计期中分析方法评价*

姜 超 刘丽亚 邵 方 于 浩 陈 峰△

【提 要】 目的 基于生存指标的无缝设计，考查PFS在什么条件下可以用于II/III期无缝设计期中分析时的剂量组筛选。方法 采用模拟试验的手段，分别研究基于生存资料下Fisher合并法和加权逆正态法在利用和不利用OS的信息两种组别筛选策略下的总I类错误率和检验效能。结果 加权逆正态合并法与Fisher合并法相比，两者在控制总I类错误率方面无明显差异，随着PFS和OS相关性增强，加权逆正态合并法的检验效能要高于Fisher合并法，并且合并PFS和OS的信息将获得更高检验效能。结论 当PFS和OS的相关性较大，且效应趋势一致时，建议采用加权逆正态合并法合并两者的信息进行II/III期无缝临床试验的统计分析。

II/III期无缝试验中，有时终点指标需要通过长时间的观察才能得到，短期内无法获得，这与需要基于终点指标快速挑选出最优剂量组进入后续试验的实际需要相矛盾。为此，人们在期中分析时往往采用短期替代(surrogate variable)指标对多个剂量组进行筛选[1]，同时对第一阶段和第二阶段的长期指标进行观察，最后基于两个阶段的长期指标作出统计推断[2]。

目前，虽然有很多学者发表了众多有关无缝设计研究方法的论著，包括Stallard和Todd提出的成组序贯法(grouped sequential design,GSD)[3]、Bauer和Keiser提出的合并检验法[4]、 Koenig等人提出的适应性Dunnett法(adaptive Dunnett test，ADT)[5]。但是其中大部分所用到的早期指标和终点指标为定量或定性指标，对于生存类型的数据，有关的研究相对较少。本研究主要探讨基于生存类型的结局指标的II/III期无缝设计，为叙述方便，本文以抗肿瘤药物临床试验为例，以总生存时间(overall survival,OS)为终点指标，这是一个长期观察指标；以无进展生存期(progression-free survival,PFS)为替代指标，这是一个短期指标。

无缝设计统计方法

假设一个临床试验最初包括一个对照组T0以及k1个试验组，T1,…,Tk1，期中分析时淘汰掉劣效组，有k2个试验组进入二阶段的研究。令θi作为Ti超过T0程度的测量值，i=1,…,k1，用于衡量试验组i与对照组之间的疗效差异。若θi>0，则Ti优效于T0。按此定义，产生了k1个原假设Hi:θi= 0，以及对应的单侧备择假设为Hi':θi> 0。检验统计量Zi,j(j=1,2)分别表示根据第一阶段或第二阶段独立数据计算所得第i组的检验统计量值，Zi,1与Zi,2相互独立。

1.期中分析的策略

期中分析时有两种策略，一是只利用短期指标筛选，不考虑长期指标的信息；二是同时考虑短期指标信息和长期指标信息。我们将对这两种策略进行比较。

短期结局指标与长期结局指标可以通过下面这个过程相结合，为了选择一个有效的剂量组进入第二阶段的研究，我们用公式(1)将搜集的PFS和OS的信息合并[6]。

utilj=wj·probj,PFS+(1-wj)·probj,OS

(1)

其中probj,Obs表示第j阶段根据观测的数据计算的相应概率值，wj表示两个阶段信息的权重。关于权重有不同的建议[6]，其中一种如下：

(2)

其中d1j,PFS和d1j,OS分别表示试验组j在期中分析时进展和死亡的事件数，死亡事件赋予2倍权重。

2.信息合并的方法

由于最终的统计推断是基于两个阶段获得的主要结局数据进行的。因此在这个过程中就存在了对两个阶段的统计信息进行整合的问题，该问题可以通过以下两种信息合并的方法解决。

(1)Fisher合并检验法

Fisher合并检验法是Fisher在1932年[7]提出的，表达式如下：

(3)

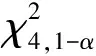
(2)加权逆正态法

该方法由Mosteller和Bush[8]在1954年提出，表达式为:

C(p1,p2)=1-Φ(w1Φ-1(1-p1)+w2Φ-1(1-p2))

(4)

上述两种方法均为合并检验法。1999年，Bauer和Kieser[9]提出将合并检验应用于无缝设计的基本思想。该方法是运用闭合检验过程及合并检验过程来实现多重假设检验，其优点在于适用各种合并检验方法以及任意一种交集假设。

模拟试验

(5)

=ρ

对于生存资料仍可沿用正态分布理论，此时，θ表示为logHR，信息量I则为log-rank检验原假设条件下的方差[10]。

log-rank统计量比较的是在各个观测事件时间点的两组风险函数的估计值，该统计量的构建可以通过计算各事件时间点每组观察到的事件数与期望事件数的差值，然后再求和以获得对所有事件时间点的总体概括。令j=1,…,J为每组观测到事件的具体时间点，O1j和O2j表示各组在时间点j观测到的事件数并且定义Oj=O1j+O2j。考虑到在时间点j两组中有Oj个事件发生，那么在H0假设下，O1j服从参数为Nj,N1j和Oj的超几何分布，这个分布的期望为E1j,方差为Vj。因此，log-rank统计量比较每一个O1j和它的期望值E1j，在H0假设下可以表示为以下：

(6)

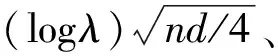
(7)

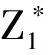
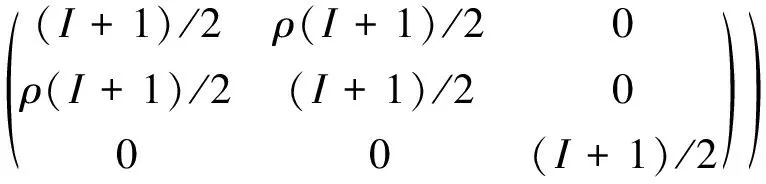
(8)

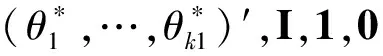
因此在进行模拟试验时，我们通过设置不同组的中位生存时间，通过计算各试验组的HR来模拟产生在分析时会得到的log-rank统计量。短期指标与长期指标的相关性，我们通过在上述方差协方差矩阵中设置，在考查总一类错误率时，我们设置各组长期指标的中位生存时间相等，在考查检验效能时，我们设置其中某一组的中位生存时间不等。由于组别筛选仅根据短期指标，最终的分析时合并的统计量是由模拟产生并且与HR有关，因此在模拟试验中并未考虑截尾问题。

1.模拟试验A

(1)试验目的

通过模拟试验考察PFS、OS间相关系数的大小对总I类错误的影响，并探讨在Bonferroni[12]法和Hochberg[13]法两种校正方法下，Fisher合并检验法(FCM)、加权逆正态法(WINM)对总I类错误的控制情况，同时考虑使用和不使用OS的部分信息两种策略，观察各种方法之间的差异。

(2)试验步骤

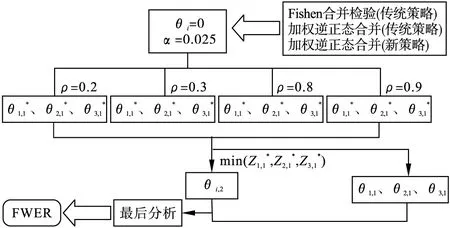
图1 模拟实验A步骤

(3)参数设置见表1

表1 模拟试验A参数设置

(4)主要结果

模拟试验结果见表2、表3。其中FCM(PFS)表示Fisher合并法只考虑PFS，WINM(PFS)表示加权逆正态法只考虑PFS，WINM(PFS+OS)表示加权逆正态法同时利用PFS和OS的信息。

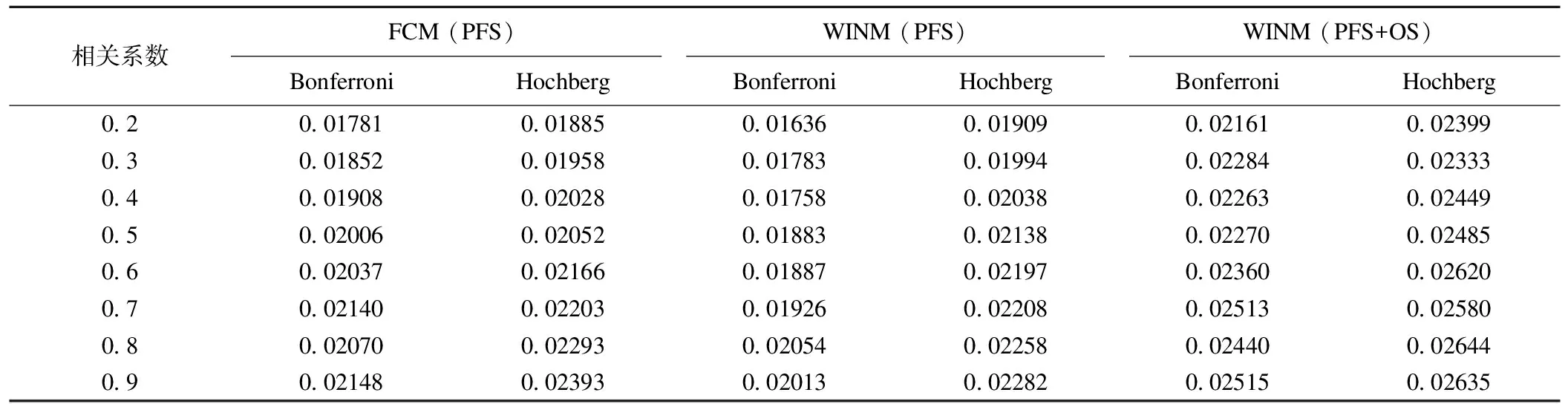
表2 在不同相关系数时，三种情景的总I类错误率(θ1=θ2=θ3=θ1*=θ2*=θ3*=0)

表2给出的总I类错误率表示的是错误地拒绝任意一个真实原假设的概率(FWER)，理论上FWER应该接近设定的0.025。

这部分结果表明：从试验结果可以发现，模拟的两种方法的错误率均控制在理论范围内或接近理论值。随着相关系数的降低，总I类错误率也随之降低。这源于试验组的筛选基于PFS，然而多重校正原本是根据OS筛选最优试验组。如果ρ=0,用于筛选的PFS和OS是相互独立的，意味着试验组的选择是随机的。随着ρ增大，PFS的筛选结果越有可能与根据第一阶段OS筛选结果相一致，所以保守性得以改善。

在仅采用PFS信息进行组别筛选的策略下，在Fisher合并检验法和加权逆正态法中，分别用Bonferroni法和Hochberg法进行多重比较校正，可以看出Bonferroni较Hochberg法保守。而在采用合并PFS和OS信息策略下，Bonferroni法较Hochberg法能更好地控制总I类错误。所以，在后面的研究中，在策略1下，Fisher合并检验法和加权逆正态法中统一采用Hochberg法。在策略2下则采用Bonferroni法。

两种方法的总I类错误差异并不明显，总体来说加权逆正态法对α的控制略为严格。无论是否合并OS信息，都能很好控制总I类错误；合并OS信息的策略更接近检验水准，而不合并OS信息，仅应用PFS信息，结论将趋于保守。

表3 不同相关系数和θ1*时，三种情景的总I类错误率(θ1=θ2=θ3=θ2*=θ3*=0)

表3考察的是当3组试验组与对照组的长期疗效没有差异的情况下，其中一组试验组的短期指标提示有疗效时，对总I类错误率的影响。总体来说，总I类错误率控制在理论水平，随着HR值的降低，相关的作用越低，总I类错误率也越来越趋于ρ=0的情形。

2.模拟试验B:相关系数对检验效能的影响

(1)试验目的

探讨PFS和OS不同相关系数时三种情景下的检验效能趋势和相互间的差异。

(2)试验步骤

设置不同的相关系数和PFS差异，模拟其在不同组合下的检验效能。观察运用Fisher合并检验法、加权逆正态法两种方法及两种策略时检验效能随相关系数以及短期结局指标变化的特征。

(3)参数设置见表4

(4)试验结果

模拟试验结果见表5。

在OS的不同HR值下，检验效能的变化趋势大致相同，我们选择其中一种进行展示。

这部分的模拟结果可以表明：

虽然PFS在固定的HR值下，检验效能的差异不大，但总体而言，在仅采用PFS信息进行组别筛选的策略下，无论是Fisher合并法还是加权逆正态合并法的检验效能都随PFS和OS的相关性增强而增加。并且，就此试验而言，加权逆正态法的效能要略高于Fisher合并法。而在采用合并PFS信息和部分OS信息进行组别筛选的策略下，加权逆正态法的检验效能反而随着PFS和OS的相关性增强而降低。这是因为随着PFS和OS的相关性增加，PFS对于OS的替代性也越来越好，与此同时PFS可以在较短时间内获得，信息较为完全，而OS在早期所获得的信息较少，也不完全，容易产生偏差，在这样的情况下，采用合并两者的策略将影响期中分析时组别筛选的准确性，相应地也降低了检验效能。

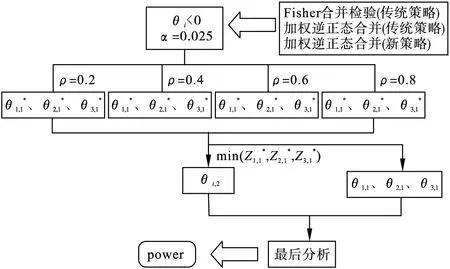
图2 模拟实验B步骤

参数意义(取值)nSims模拟次数(10000)α一类错误率(单侧0.025)λ0,λ1,λ2,λ3长期指标估计各组中位生存时间(7.5,10,7.5,7.5)λ0∗,λ1∗,λ2∗,λ3∗短期指标估计各组中位生存时间(3.5,λ1∗,3.5,3.5)λ1∗为(3.5,3.75,4,4.25,4.5,4.75,5)ρn1n2d1OS与PFS的相关系数(0.2(0.2)0.8)一阶段每组样本量(180)二阶段每组样本量(360)期中分析时出现进展事件的比率(0.67)d2d3期中分析时出现死亡事件的比率(0.2)最终分析时出现死亡事件的比率(0.6)power实际把握度

随着HR值的逐渐减小，各相关系数下的检验效能均呈上升趋势，且差异逐渐缩小，这是由于HR值越小，则有疗效的试验组被选出进入II阶段的概率就越大，只要HR值足够小，那么无论在怎么样的相关关系下，有疗效的试验组还是会被选中，此时相关系数对检验效能的影响被削弱了。

总体而言，合并部分OS信息进行组别筛选的策略，其检验效能总体要高于仅利用PFS信息的策略，尤其在PFS差异不大时。而当PFS差异逐渐增大时，合并OS信息带来检验效能增大的效应将逐渐减弱。

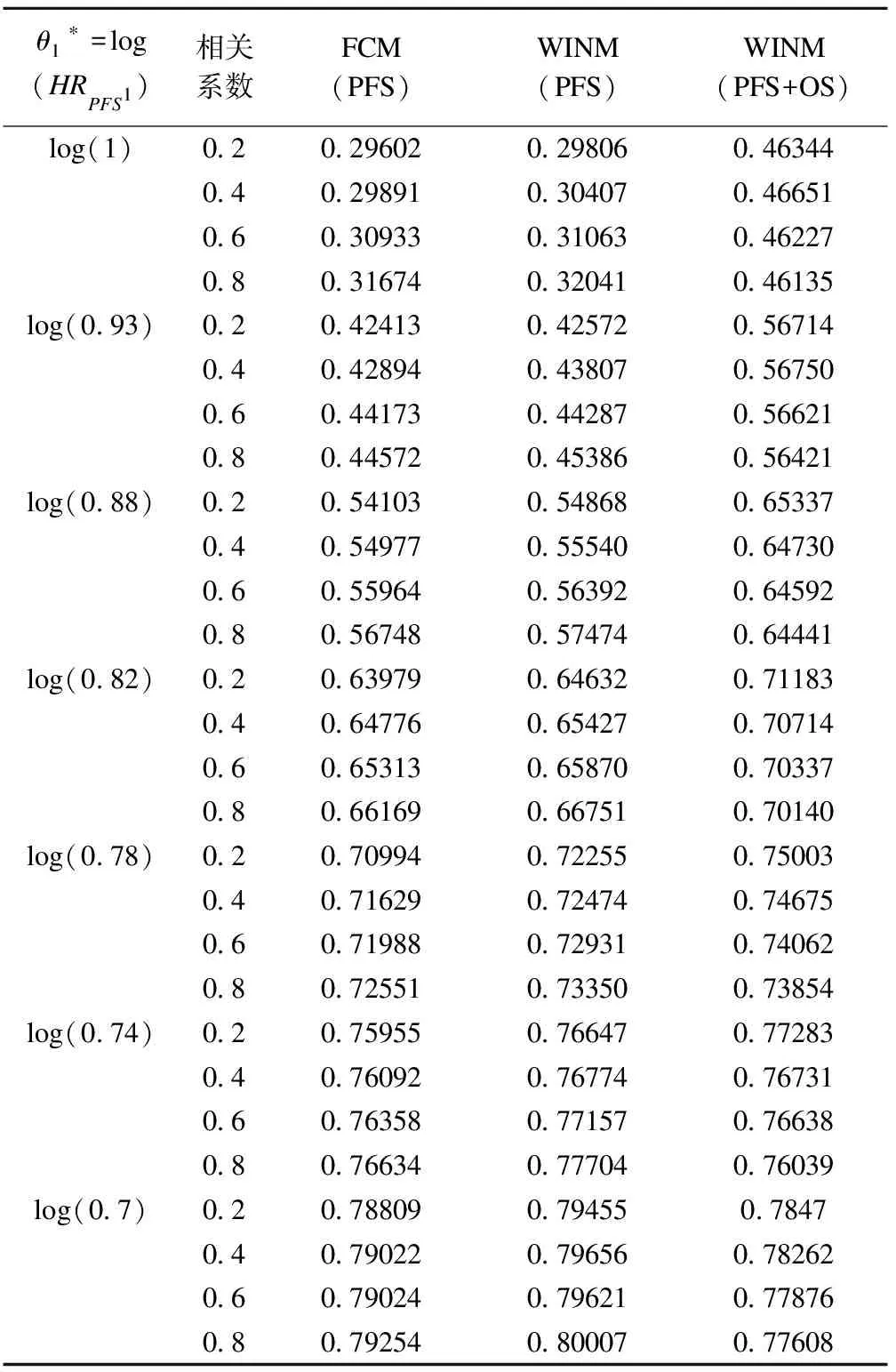
表5 在不同相关系数时，三种情景的检验效能(HROS2=HROS3=HRPFS2=HRPFS3=1,HROS1=0.7)

讨 论

抗肿瘤新药的开发是当今国际药物研究力量投入最多、投资最大的领域。但是在过去的数十年，药物研发方面花费的不断增加，而制药临床研究成功率并没有相应增加。II/III期无缝设计由于其灵活、科学且符合伦理的特点，受到了研究者和药企及其主管部门的重视，2006年，美国FDA颁布了《关键性通道机遇目录》(critical path opportunity list，CPOL)，要求进行创新的试验设计，其中一个很重要的内容就是鼓励适应性设计在临床试验中的应用[14]。但是目前为止，无缝设计尚未得到广泛应用，其主要原因在于这种方法在设计和统计分析方面仍然存在一些尚未解决的问题。

本文基于肿瘤药物研究过程中的生存资料对II/III期无缝设计组别筛选时采用的Fisher合并法与加权逆正态合并法的统计学特性进行了研究。同时研究了合并与不合并OS信息的策略对试验结果的影响。通过模拟试验可以发现，PFS与OS指标间的相关性对试验结果会有影响，相关系数越大，则说明PFS对于OS的代表性越好。若组间的差异一定，相关系数越大则检验效能也越大，总I类错误率的控制也越理想。并且加权逆正态合并法要优于Fisher合并法。相反，若相关系数越小，检验效能将逐渐下降，试验也趋于保守。将PFS作为OS的替代指标，在很多肿瘤研究中已经被成功应用，临床实践中，两者通常都保持着一定正相关关系，所以本文的模拟试验只考虑了相关系数为正值的情况。除了PFS和OS的相关性外，PFS的效应也在一定程度上影响着试验结果。PFS的效应值之所以会影响到试验结果，主要是因为期中分析时，以PFS作为OS的替代指标，并据此选择最优剂量组，短期结局指标的大小直接决定哪一组可以进入下一阶段的试验。如果短期指标与长期指标变化趋势不同，则会导致长期指标最优组与短期指标最优组不一致的情况，此时，以短期指标为基础筛选试验组，就可能会导致长期指标最优剂量组被淘汰，选入的试验组有可能是实际疗效最差的一组，而在最后分析时，采用的又是这组的长期指标数据，则必然会导致试验结果不理想，甚至发现不到疗效，造成损失。

本研究的模拟实验，虽然已经尽可能地考虑了其代表性，但也难以包含所有的复杂情况，有待进一步研究。如短期指标与长期指标变化趋势不同时；不同期中分析时间点对于上述方法统计学性质的影响；以及实际工作中可能遇到的是失访率、入组率、截尾等对其的影响。