项目反应理论在健康相关量表中的应用现状及展望*

哈尔滨医科大学(大庆)护理学院(163319) 王伟梁 周郁秋

项目反应理论(item response theory，IRT)属于现代测量理论的一种，是针对经典测量理论(classic test theory，CTT)在实践中的局限性而提出的，其主要优点为参数和能力估计的不变性[1]。除此之外，IRT在量表编制中优于CTT的三个特点：CTT注重量表的整体特性，而IRT则关注构成量表的每一条目的特性；根据待测潜在特质水平选择项目；对项目和量表特性的视觉化表示[2]。其在健康相关领域中的应用，使量表在评估被试潜在特质的精确度及临床应用的简洁性、效率化上有一定的提高。鉴于以上优点，近年来IRT在量表编制和评价中得以广泛应用。本文通过检索国内关于IRT应用于健康相关领域的研究，分析其在健康相关量表编制和评价中的应用现状，并总结IRT在应用过程中存在的问题以及最新的应用动态。

本文通过检索知网、万方和维普数据库，共筛选出86篇相关文献，文献的基本信息见表1。结合数据分析可以看出，近年来文献数量有了很大的增长，2010年至今，相关文献达74篇(86%)，从这一发展趋势看，今后IRT势必会成为量表编制和评价中的应用热点。但在文献数量增加的同时，文献质量也呈现出参差不齐。存在的主要问题为：一是部分研究只根据经验来选择模型，而缺少统计学的评价；二是研究中未重视IRT的基本假设检验；三是部分研究样本量未达要求。这样得出的结果就会有很大的误差。IRT的理论基础较为难懂，限制了其广泛应用，同时国内相关应用相对较少，缺少参照标准，均导致大多研究者未意识到或忽略上述问题对于IRT分析的重要性。

IRT在量表编制和评价中的应用

1.条目筛选

IRT的条目筛选是通过一系列的参数估计来实现的，具体包括区分度参数(a)、难度参数(b)、项目信息量(information function，IF)和项目功能差异(differential item functioning，DIF)。从检索到的文献来看，应用最多的是a、b和IF，但不同研究所依据的参数参考范围有很大差别。

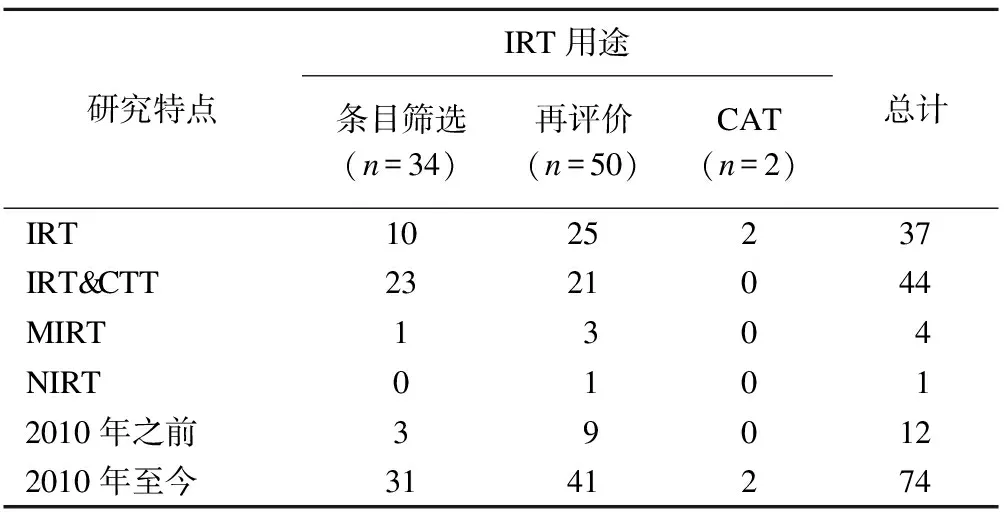
表1 IRT在国内健康相关量表研究中的应用现况

*：量表再评价包括已有量表条目质量评价、简化和DIF；CAT：计算机适应性测验;MIRT:多维项目反应理论；NIRT：非参数项目反应理论。

(1)难度和区分度：难度和区分度的理论取值范围均为[-∞，+∞]，但在实践中通常采用的参考值范围分别为∈[-3,+3],a[-2.80,+2.80][3]。也有研究表明：在健康相关领域中，由于测量的潜在特质概念界定相对狭窄，应用IRT参数估计出的区分度值总体偏高，此时仍参照[-2.80,+2.80]已无实际意义，为挑选最佳量表条目，会在其研究中对区分度范围重新界定[4-5]，但不应超出以上范围；(2)信息量：一般认为量表信息量>25表明条目质量良好；信息量16～25表明测评条目有待改进；信息量<16表明测评条目很差。16和25与条目个数的比值即为每个条目的平均信息量参考范围，条目信息量小于平均信息量的建议删除[6-7]；(3)项目功能差异：质量高的量表条目被认为其对不同亚组人群(年龄、性别等)的潜在特质鉴别上应没有差别。当同一条目在两个亚组中的平均阈值差异大于0.5，则可认为该条目存在DIF，考虑删除[8]。

检索到的相关文献中，23篇(72%)采用IRT结合CTT进行条目筛选。CTT注重的是量表的宏观评价，即量表的整体特性，IRT注重的是量表的微观评价，即每一条目的测量学特质，所以在量表条目筛选中，建议结合IRT和CTT对量表条目进行综合评价，评价结果一致，则为条目的取舍提供更强的说服力;评价结果不同，则有助于我们从不同角度分析问题，找出原因所在，为条目的筛选提供更宽的视角。

2.量表再评价

量表简化：IRT在量表编制中的一大特点为用最精简的条目反映最大的信息量。一些基于CTT编制的量表，有必要在IRT下进行进一步的简化，提高临床和科研效率，减轻被试负担，增强其临床适用性[9-10]。量表结构和条目质量评价：为使量表整体和条目质量达到最优化，许多研究者将已有量表在IRT的基础上对其维度结构和条目质量再次评价，使其更好地应用于临床实践[11-13]。

3.计算机适应性测验(computerized adaptive testing,CAT)

CAT主要是根据受试者的答题反应，利用计算机选出符合受试者程度值的题目让其作答，因此只需要少数题目就能达到与传统非适应性测验相当的测量精准度[14]。CAT一般应用于大型的人格或能力测验，在健康相关量表中的应用很少，在检索到的国内相关文献中，仅有Yang等[15]在其研究中对急性压力反应量表临床测评应用了CAT，而国外近几年将CAT应用于健康相关量表评价的研究则较多[16-19]。

IRT近年来在量表编制和评价中的应用逐渐受到重视，而临床广泛使用的量表评价工具都是在CTT的基础上发展而来的，往往带有CTT固有的局限性，所以有必要在现代测量理论的基础上进行量表特性的再分析评价，使其更好地应用于临床实践；量表简化和CAT在科学的基础上，保证测量精准度不变的情况下，大大提高临床和科研效率，更加符合实践应用的要求。

IRT在应用中需注意的问题

IRT是建立在复杂的数学模型基础上的，其应用条件相对严格，只有数据符合IRT的基本要求时，其优越性才能体现出来，否则，IRT的参数估计就无实际参考意义。结合IRT在国内健康相关量表中的应用状况分析，其主要问题为样本量和假设检验。

1.模型拟合检验

选择合适的模型是保证IRT数据分析结果准确性的前提。从检索到的文献来看，仅1篇(1.2%)从统计学角度评估模型适配程度，大多数模型的选择是依据相关经验或文献回顾，而缺少统计学的评价指标。除Rasch模型外，其他模型的拟合检验均是通过嵌套模型之间的对比间接评价的，常用的统计评价指标为对数似然函数值(-2 Log Likelihood)，其值越小，表明模型-数据拟合越好，目前IRTPRO、BIOLOG、MUITILOG、PARSCALE及Stata14.0等软件均可进行这一参数估计。除此之外，还有S-G2、S-χ2等也可用于评价模型拟合的好坏[20]。除模型拟合检验外，往往还需要进行条目拟合检验，在条目水平上评估模型与实际资料是否相吻合,可用于筛选量表中的个别条目[8,21]。

2.假设检验

IRT建立在很强的假设基础上，要满足相应的假设检验，得出的参数估计才有意义，否则，会出现很大的误差。项目反应理论的两个重要的基本假设即单维性和局部独立性。目前检索到的文献中，共30篇(34.0%)进行了单维性检验，而仅3篇(3.4%)文献中进行了局部独立性检验。

(1)单维性检验

单维性即所有量表条目反映的是同一潜在特质。所有的IRT模型(除MIRT)均需要单维性检验，而大多数的研究中往往忽略这一点，一是因为部分研究者未意识到单维检验对数据分析的重要性，二是相关统计方法不明确。参考国内外相关研究，单维性检验的方法有：特征根比值法[22-24]、主成分分析[25]、平行分析[26]和残差分析[27]。其中特征根比值法最为常用。

(2)局部独立性检验

局部独立性即被试的潜在特质是影响被试反应的唯一因素，此假设是建立在单维性假设的基础上的，只有单维性假设成立，该假设才有可能成立。

局部独立性检验的方法有(1)残差相关：验证性因子分析的残差相关来检验条目间独立性，残差相关绝对值≤0.3，表示局部独立性假设成立[28]；(2)X2检验：Chen和Thissen建议局部独立性χ2值≥10，表示假设成立[29]。此外还有G2检验、Q3检验等[30]。

局部独立性检验是IRT应用的一个前提，然而诸多学者建议，在认为能力是单维的情况下，局部独立性和单维性假定是等价的，即数据只要满足单维性检验，就一定符合局部独立性[24,31-32]。因此，建议在实际应用中，若数据很好地满足单维的标准，则可以认为单维性和局部独立性是等价的。

3.样本量

IRT的不同模型对样本量的需求尚无统一标准，模型越复杂，需要的样本量越大。Linacre等[33]建议Rasch模型(1PL)参数估计时样本量至少100例，而Wright等[34]则建议至少要达到200才能得出稳定结果；Hulin等[35]建议双参数模型(2PL)至少需要500被试，参数估计才具有准确性；对于三参数模型(3PL)，样本量则至少要达到1000。而等级反应模型(GRM)至少需要250例数据才能得出准确的参数估计[36]。

总的来说，样本量越大，条目的参数估计越准确,得分的标准误差越小[37]。本研究检索到的86篇相关文献中，样本量范围为133～7229例，其中20篇(23%)存在样本量过小的问题，最小的样本量仅133例(非Rasch模型)，这样估计出来的参数显然是不可靠的。在健康相关领域中，由于某些疾病本身特点的影响，使样本量的可及性受到一定的限制，在模型和基本检验较好的情况下，样本量可适当缩小，但不应低于最低要求。

项目反应理论的发展

IRT的参数估计依赖于一系列的假设基础，而实际的数据往往难以满足IRT的基本假设，给实践应用造成很大的不便，这就使得近年来在IRT基础上发展的多维项目反应理论(multidimensional item response theory,MIRT)和非参数项目反应理论(nonparametric item response theory,NIRT)受到更多的关注。

1.多维项目反应理论

对于不满足单维性假设的数据，MIRT为其提供了替代方案。对于健康相关量表而言，测量的潜在特质往往是多维的，且量表维度跨度较大，维度之间同质性较差，所以较难满足单维假设。目前，对于不满足单维假定的数据有两种处理方法：整体量表不满足单维性，分每个维度进行单维性检验，若满足，进行进一步分析[38-39]；应用MIRT处理数据[15,40]。然而若将每个维度单独进行检验和参数估计，则忽略了量表整体之间的相关性，测量结果也会受影响。所以在数据不满足单维时，MIRT应作为首选。

2.非参数项目反应理论

NIRT不是通过一系列的参数估计来评价被试的潜在特质水平，而是直接按被试在测试中所得的分数进行排序，从而得出被试特质水平的高低[41]。由于其对基本假设和样本量要求相对宽泛，国外已有诸多研究将NIRT应用于健康相关量表的评价[9,11]。

展 望

IRT因其在量表应用中的显著优点，近年来相关研究日渐增多。在条目筛选中，IRT结合CTT将从不同角度为量表条目筛选提供更加全面的依据；量表再评价、简化以及CAT将大大提高量表测量工具在临床应用和研究中的效率，以最简洁、优质的条目准确地评估被试特征，在今后的相关研究中应更多地引入IRT。同时，IRT建立在复杂的数学模型基础上，依赖于较强的假设，对数据要求比较严格，所以国外研究近年来较为推崇MIRT和NIRT,而国内在这方面的应用则非常有限。本文对IRT在我国健康相关量表中的应用现状进行了分析总结，并对应用中存在的问题及近年来国外研究中的应用热点进行了介绍，为今后IRT在我国量表编制和评价中更为广泛的应用提供参考。