大样本数据标准化率的SAS宏实现*
2018-09-20夏雷震HeziFu刘红波
夏雷震 Hezi Fu 金 城 缐 伟 刘红波△
流行病学研究过程中,经常会遇到率的比较问题,当各组观测的内部构成,诸如年龄、性别等存在较大差异时,直接比较各组的粗率(合计率)是不合理的,通常应该对其进行标准化来消除内部构成不同的影响。对于小样本数据,一般只涉及几组率的比较而不是多组率的比较或者是内部构成简单(比如只有年龄这一混杂因素),通常结合统计相关教材借助Excel就能较容易、简单的计算出标准化率;但在这个信息化时代,我们经常会遇到复杂嵌套关系下的多层次组群结构的海量数据,如各省市疾病预防控制中心的传染病报告数据、疾病死亡数据,某疾病各年份患病情况等,对这种含有多个混杂因素、多分组的数据,利用教材里公式和Excel的统计汇总功能来计算标准化率常常会遇到很大的困难,且计算过程繁琐容易出错[1-2],这时我们最好借助统计软件来完成[3]。SAS是最常用的数据处理和统计分析的软件之一,本研究通过编写SAS宏程序实现大样本数据率的标准化,希望能够帮助科研工作者更加方便快捷的解决标准化率的计算问题。
基本原理
率的标准化法就是在指定的标准构成条件下计算标准化率,以便于对多组率进行对比。对于标准人群的选择有三种方法,分别是任选一个对比组的人群、各组人群之和以及有代表性的、稳定的、数量大的人群,如全国、全省的数据[4],选择前两种人群的标准化法称为直接法,选择后一种人群称为间接法。无论是直接法还是间接法,它们标准化的基本思想是先计算出标准人群的内部构成比例(比如年龄构成比)当作权重qi,再计算出各组别(比如各地区)各年龄段的率Pij,最后对各地区计算各年龄段的加权算术平均数∑qiPij[5]。一般情况下,对标准人群的选择会选择后两种,即以各组人群的总和为标准人群计算直接法标准化率和以具有代表性的全国人口为标准人群计算间接法的标准化率,所以本研究以这两种人群作为标准人群对率分别进行直接标准化法和间接标准化法。
实例分析和SAS宏实现
实例:结节病是一种免疫系统疾病,其发病机制和病因不明确。文献报道结节病的发生和死亡与年龄、性别有关,也表现出地域性差别。某研究者欲了解结节病的发病特征,调查了2014年的5个地区的47780名在职及退休职工,记录结节病患病情况,原始数据std.sar形式如表1。
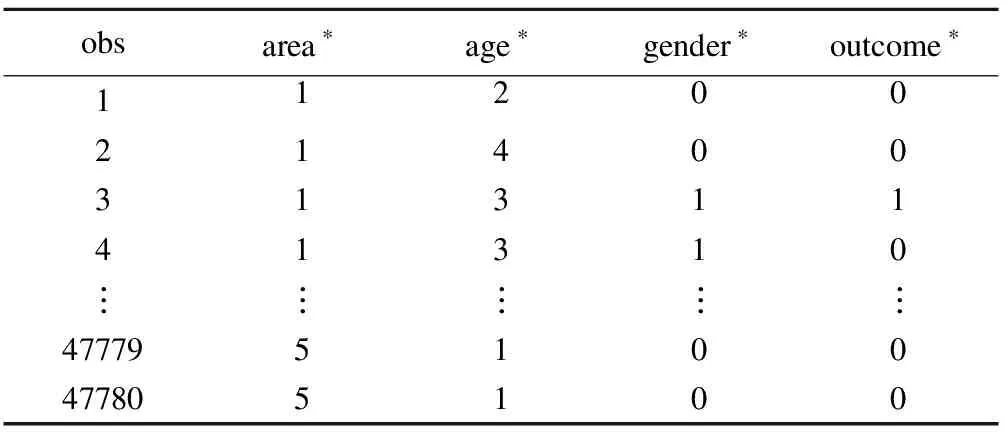
表1 实例中原始数据的形式
*area:1~5代表5个区;age:1~6代表6个年龄段;gender:1=男,0=女;outcome:1=患病,0=不患病
1.选择所有地区的人口作为标准人群做直接法的标准化率
SAS宏命令如下:
%macro direct_std(data=,outcome=,group=,confounder=,confounder_=);
data standardization;
set &data.;
keep &outcome.&group.&confounder.;
run;/*提取数据中有用的信息*/
proc summary data=standardization nway;
class &group.;
var &outcome.;
output out=crude(drop=_:) n=N sum=cases;
run; /*汇总原始数据五个地区的总人数N,发病人数cases*/
data crude;
set crude;
crude=cases/n;lower_CI=crude-1.96*sqrt(crude*(1-crude)/n);upper_CI=crude+1.96*sqrt(crude*(1-crude)/n);
run;/*计算粗率crude及应用二项分布的正态近似法计算置信区间[5-7]*/
proc summary data=standardization nway;
class &group.&confounder.;
var &outcome.;
output out=summary(drop=_:) n=N sum=cases;
run; /*汇总原始数据各地区各性别年龄别的人数N,发病人数cases*/
data summary;
set summary;
p=cases/n;
run;/*计算各地区各性别年龄别的发病率p */
proc sort data=summary out=summary;
by &confounder.;
run;
proc sql;
create table summary as select *,sum(n) as totall from summary group by &confounder_.;
quit;/*此命令group by后面的变量间需要逗号隔开,故而重复设置了confounder_宏参数*/
proc sql;
create table summary as select *,sum(n) as total2 from summary ;
quit;
data summary;
set summary;
ratio=total1/total2;
run;/*计算以各组人群的总和为标准人群的内部构成(性别年龄别)的构成比ratio */
data summary;
set summary;
rate=p*ratio;
run;
proc summary data=summary nway; class &group.; var rate; output out=adj_rate(drop=_:) sum=adj_rate;
run; /*对各地区按照构成比ratio为权重计算各年龄性别组发病率p的加权算术平均数adj_rate,即为标准化率*/
data adjust;
merge crude adj_rate;
drop cases crude lower_ci upper_ci;
run;
data adjust;
set adjust;adj_cases=n*adj_rate;adj_lower_CI=adj_rate-1.96*sqrt(adj_rate*(1-adj_rate)/n);adj_upper_CI=adj_rate+1.96*sqrt(adj_rate*(1-adj_rate)/n);run;/*计算标准化率adj_rate的置信区间*/
data adjust;
retain area N adj_cases adj_rate adj_lower_CI adj_upper_CI;set adjust;
run;
title “粗率及其置信区间”;
proc print data=crude;run;
title “标准化率及其置信区间”;
proc print data=adjust;run;
%mend;
消除年龄和性别的影响计算各地区结节病标准化患病率的宏参数设置如下:
%direct_std(data=std.sar,outcome=outcome,group=%str(area),confounder=%str(age gender),confounder_=%str(age,gender));
结果输出为:
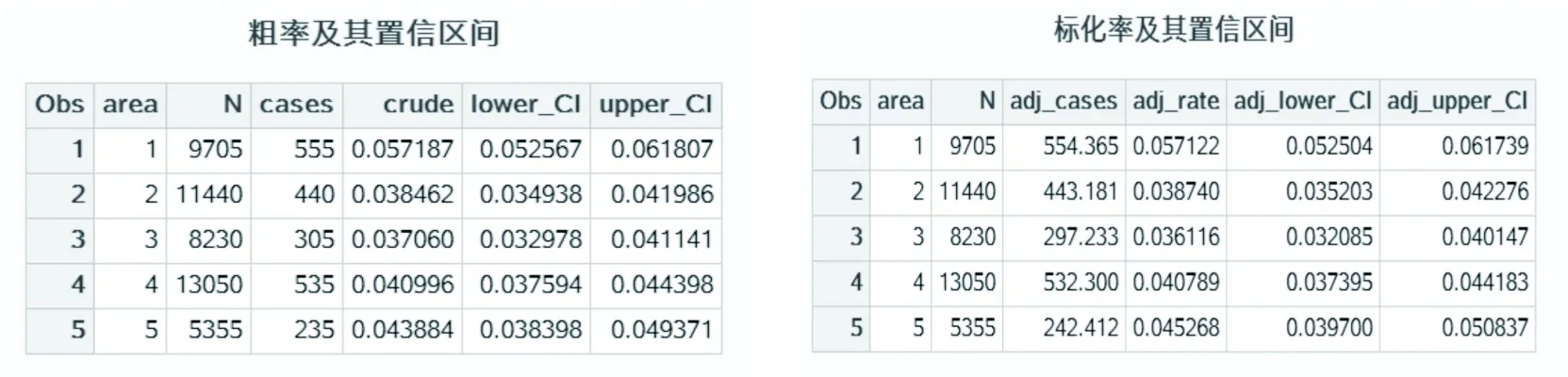
所有结果也可在文件work.crude和work.adjust中查看和导出。如果想消除年龄的的影响计算各地区分性别的结节病标准化患病率的宏参数设置如下:
%direct_std(data=std.sar,outcome=outcome,group=%str(area gender),confounder=%str(age),confounder_=%str(age));
以此类推。
在实际工作中,有时收集不到原始数据std.sar,
只有汇总数据std.sar2,同样可以计算标准化率,数据形式为:
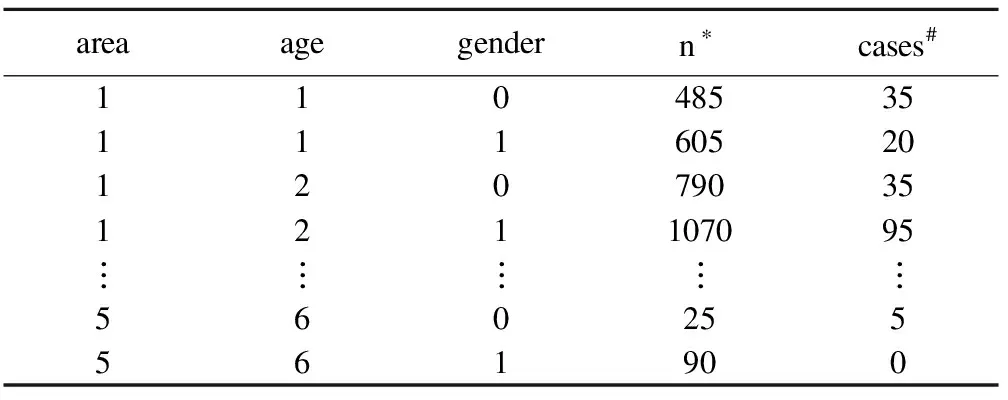
表2 汇总数据的形式
*:不同地区各年龄性别的总人数; #不同地区各年龄性别的患病人数
SAS宏及宏参数设置如下(其中省略部分与上文SAS宏对应位置一致):
%macro direct_std(data=,group=,confounder=,confounder_=,n=,cases=);
data standardization;
set &data.;
keep &group.&confounder.&n.&cases.;
run;
proc summary data=standardization nway;
class &group.;
var &n.;
output out=crude1(drop=_:) sum=n;
run;
proc summary data=standardization nway;
class &group.;
var &cases.;
output out=crude2(drop=_:) sum=cases;
run;
data crude;
merge crude1 crude2;
run;
data crude;set crude;crude=cases/n;lower_CI=crude-1.96*sqrt(crude*(1-crude)/n);upper_CI=crude+1.96*sqrt(crude*(1-crude)/n);run;
data summary;
set standardization;
p=cases/n;
run;
proc sort data=summary out=summary;
by &confounder.;
run;
…
%mend;
%direct_std(data=std.sar2,group=%str(area),confounder=%str(age gender),confounder_=%str(age,gender),n=n,cases=cases);
2.以全省人口作为标准人群做间接法的标准化率
SAS宏命令及宏参数设置如下:
%macro indirect_std(data=,group=,confounder=,n=,cases=,ratio_data=,ratio=);
data standardization;
set &data.;
keep &group.&confounder.&n.&cases.;
run;
proc summary data=standardization nway;
class &group.;
var &n.;
output out=crude1(drop=_:) sum=n;
run;
proc summary data=standardization nway;
class &group.;
var &cases.;
output out=crude2(drop=_:) sum=cases;
run;
data crude;
merge crude1 crude2;
run;
data crude;
set crude;
crude=cases/n;lower_CI=crude-1.96*sqrt(crude*(1-crude)/n);upper_CI=crude+1.96*sqrt(crude*(1-crude)/n);
run;/*以上为计算粗率及其置信区间的代码,与前文一致,不赘述*/
proc sort data=&data.out=standardization; by &confounder.; run;
proc sort data=&ratio_data.out=std; by &confounder.; run;
data summary; merge standardization std; by &confounder.;run;/*合并汇总数据与标准人群构成比数据,注意两个数据相同的变量名设置要一样,比如都为age、gender*/
data summary; set summary; rate=&ratio.*&cases./&n.; run;
proc summary data=summary nway;
class &group.;var rate;
output out=adj_rate(drop=_:) sum=adj_rate;
run; /*对各地区按照构成比ratio为权重计算各年龄性别组的加权算术平均数adj_rate,即为标准化率*/
data adjust;
merge crude adj_rate;
drop cases crude lower_ci upper_ci;
run;
data adjust;
set adjust;
adj_cases=n*adj_rate;adj_lower_CI=adj_rate-1.96*sqrt(adj_rate*(1-adj_rate)/n);adj_upper_CI=adj_rate+1.96*sqrt(adj_rate*(1-adj_rate)/n);
run;
data adjust;
retain area N adj_cases adj_rate adj_lower_CI adj_upper_CI;set adjust;
run;
title “粗率及其置信区间”;
proc print data=crude;run;
title “标准化率及其置信区间”;
proc print data=adjust;run;
%mend;
%indirect_std(data=std.sar2,group=%str(area),confounder=%str(age gender),n=n,cases=cases,ratio_data=std.ratio,ratio=ratio);
其中,数据集std.sar2为汇总数据的形式,如果要对原始数据std.sar运行此宏,只需对原始数据运行如下命令:
proc summary data=std.sar nway;
class area age gender;
var outcome;
output out=std.sar2(drop=_:) n=N sum=cases;
run;
数据集std.ratio为全省人群年龄性别构成比,数据形式如下:
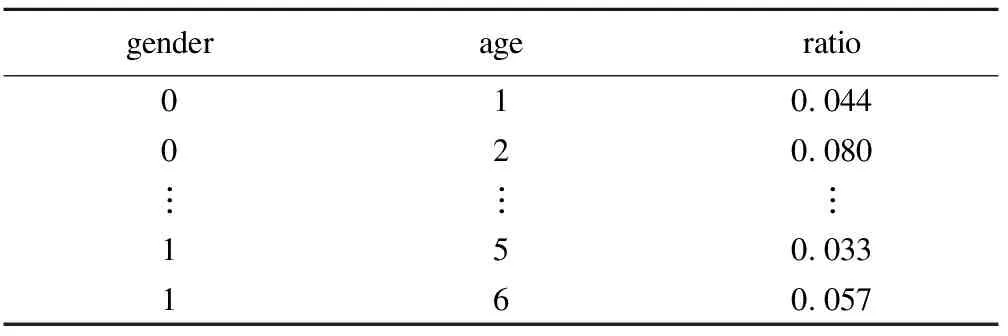
表3 某省人群年龄性别构成比
结果输出为:
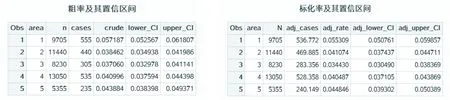
结 语
率的标准化是在疾病的流行病学研究中经常会遇到的问题,而大部分教材只介绍了按照公式计算的方法[5],但在实际工作中,经常会遇到多层次组群结构的大样本复杂数据,公式的计算常常会有较大的困难,常用的数据处理软件也没有专门的模块来解决这个问题。因此,我们通过上述实例系统的解决了对率进行直接标准化和间接标准化问题,读者可以根据实际情况选择相应的SAS宏,通过宏参数设置相应的需要比较的组别和需要消除的混杂因素,并且调整好数据形式就可以简单、快捷的计算出标准化率。
