数值解法在燃烧室出口燃气温度计算中的应用
2018-09-17王明瑞李亚娟
韩 冰,王明瑞,李亚娟,马 征
(中国航发沈阳发动机研究所,沈阳110015)
0 引言
随着航空发动机推重比的不断提升,燃烧室出口温度越来越高,燃气分析法作为1种间接测温方法,在高温升燃烧室出口温度场的测试中应用越来越广泛[1]。燃气分析测温法是集热力学、数值解技术和程序设计于一体的工程测试技术。高温燃烧产物是多成分的复杂混合物,根据热力学知识利用燃气中各成分建立物质守恒、化学平衡、压力和能量守恒方程构成非线性方程组,对其求解即可得到化学平衡组分和燃气温度[2]。
目前非线性方程组的求解没有通用的解析方法,只能通过数值计算方法获得,非线性方程组的解法长期以来都是数值计算领域的重要研究内容,已经产生了许多有效求解理论和方法,牛顿-拉夫森法是求解非线性方程组的经典算法[3-4],突出优点是收敛速度快,缺点是为了得到方程组确切解,需要保证给定的初值接近实际解,否则迭代不易收敛。针对燃烧室各种工作条件,比如燃烧室中不同的油气比、工作压力以及燃料组成等相关非线性方程组的计算求解,通用的初值很难确定,只能根据具体算例反复尝试给定[5-7]。在求解非线性方程组时,如何确定初值和迭代是否收敛以及收敛速度的快慢是燃气温度计算所关注的问题。本文采用双变量迭代法和赫夫法,不仅易确定初值,而且2种算法的迭代收敛速度都很快,通过VB编程实现非线性方程组的求解方法,并将算法成功应用于燃烧室出口燃气温度测试中。
1 非线性方程组的建立
燃烧室燃烧产生的高温反应产物是1种多成分的复杂混合物,对于燃烧室中的稳态燃烧过程,通常采用这样的假设:由于气体的停留时间较长,燃气成分的化学平衡能够建立,可以认为燃烧室出口燃气处于化学平衡状态。而碳氢燃料和空气的燃烧产物平衡成分一般由 CO2、CO、H2O、Ar、O2、N2、H2、OH、NO、O、H、N共12种成分组成,根据这些成分计算燃烧温度可满足计算需求。
通过列出物质守恒、压力、化学平衡和能量守恒方程构建非线性方程组[8-9]。
1.1 物质守恒方程
设定燃料分子式为CHaObNc,根据1 kg原始反应物与燃烧后生成的1 kg燃气各元素物质的量相等原则列出碳、氢、氧、氮、氩的守恒方程

式中:As=p·Mg,Mg为燃气的物质的量;f和 ω 分别为燃烧室油气比和进口空气的质量含湿量;RO2、SN2、TCO2和DAr分别为O2、N2、CO2和Ar在空气中的体积分数;Ma、Mf、Mω分别为空气、燃料和水蒸气的物质的量;pi为燃气中各成分分压;Ni表示1 kg原始反应物中各元素的物质的量。
1.2 压力方程

式中:p为燃烧室的工作压力。
1.3 化学平衡方程
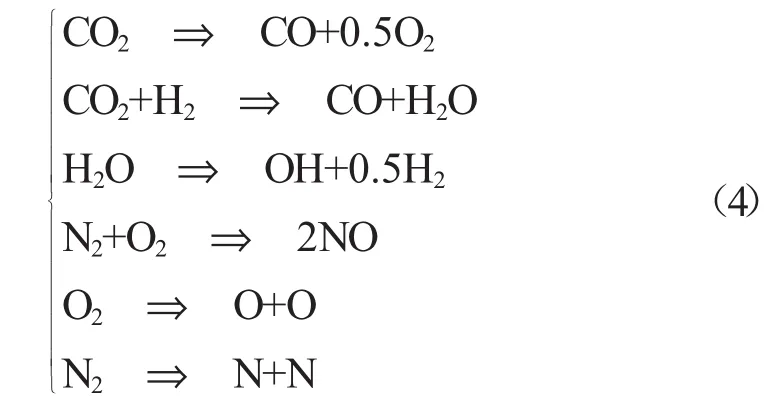
根据化学反应式(4)建立以平衡常数表示的化学平衡方程
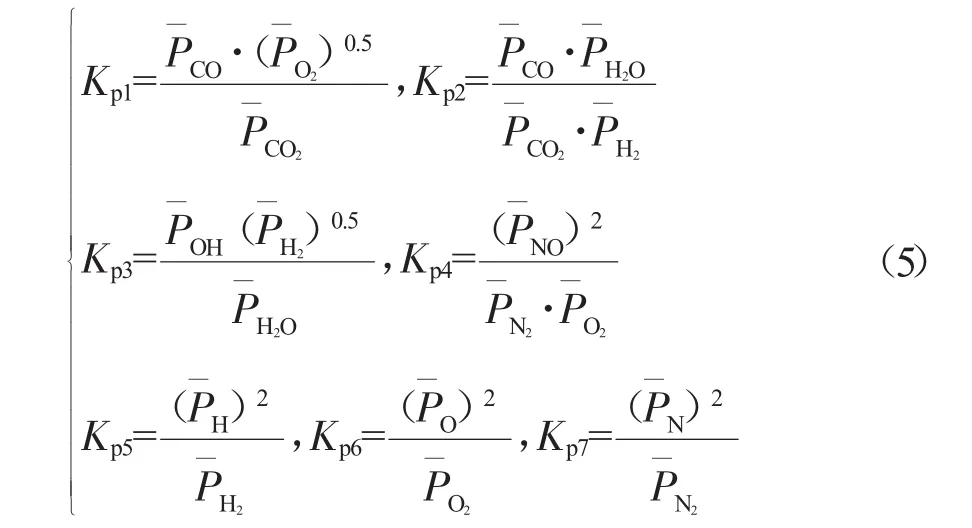
式中:Kpi为按气体分压计算的化学平衡常数;p¯i为pi与标准状态压力p0之比,p0=101325 Pa。
1.4 能量守恒方程
碳氢燃料与空气燃烧的通用化学反应式为
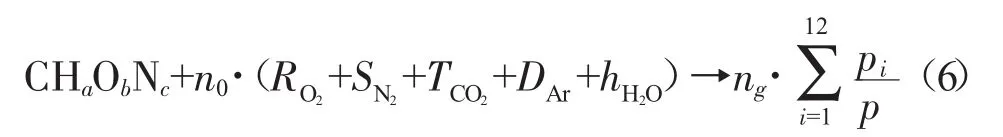
式中:n0为参与燃烧空气的物质的量,根据已知油气比可通过式(7)求出;ng为燃烧生成燃气的物质的量,在计算出燃气各组分的物质的量百分数后通过任意1种元素的物质守恒方程求出,如可利用碳元素守恒式(8)求出;hH2O为燃烧室进口空气中的物质的量含湿量。
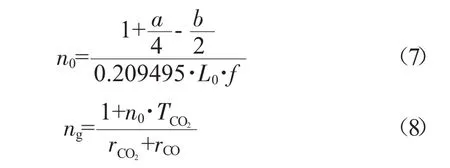
式中:a、b与CHaObNc中的下标是同一含义,为燃料中氢和氧的原子数;L0为单位质量燃料完全燃烧所需理论空气质量;rCO2和rCO为燃气中CO2和CO的物质的量百分数,其中
根据式(6)建立能量守恒方程

式中:Qf为燃料的低热值;η为燃气热态平衡时的燃烧效率,根据燃气中未燃组分,包括离解组分可以计算其值;d0为定温燃烧焓差;Hi,T为各组分在温度T的焓值;T3为燃烧室进口空气温度;T4为燃气温度。
式(1)、(3)、(5)、(9)构成非线性方程组,其中未知变量包括12种气体组分分压pi、As和燃气温度T4共14个。
2 数值解法的应用
求解非线性方程组的根本目的是获得燃气温度,引入的双变量迭代法和赫夫法主要用于求解化学平衡组分,下面具体介绍2种数值解法在燃气温度计算中的应用[10-11]。
2.1 双变量迭代法
双变量迭代法的基本方程式可以参考文献[12],该算法的基本原理是给出pN2和pO2的初值,通过该算法变换后的方程组计算出其他变量和pN2、pO2新的数值。经过大样本计算验证一般取pN2=0.780881p、pO2=0.209495p作为迭代初值,可以保证对燃烧室各种工作条件下的迭代计算都有效收敛。针对贫油燃气,采用双变量松弛法同时迭代方案计算更为快捷,迭代公式为
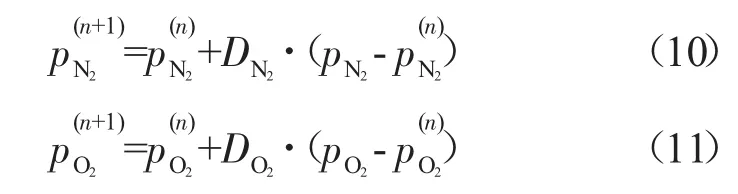
当T>3000 K或者富油时,采用双变量同时迭代一般不易收敛,此时采用双变量分别迭代可满足计算收敛,即先固定pN2值,对pO2进行迭代,然后再对pN2进行迭代,如此反复迭代直至满足精度要求为止。双变量分别迭代法与同时迭代法的方程式形式基本相同,不同的是双变量分别迭代公式采用双点弦割法,如式(12)所示。双变量分别迭代方法编程相比于双变量同时迭代法要稍微复杂。

通常给定精度小于10-9p的情况下,双变量迭代法的迭代次数在数次到十几次。目前针对主燃烧室贫油燃气的工作条件,双变量同时迭代方案基本能满足计算要求,而且其计算收敛时间比双变量分别迭代要快得多。因此一般在计算主燃烧室出口温度时采用双变量同时迭代法基本能满足计算收敛。
2.2 赫夫法
赫夫法是将牛顿法各方程式和变量取对数形式后求解非线性方程组,这样处理使得燃气组分的初值可以任意给定,此外该方法对任何原始反应物和反应产物都是通用的,迭代收敛很好,而且适用于富油燃烧[13-15]。
将式(1)整理成

式中:Δi为各变量的修正量;Ri、fi为过程计算量,无实际意义。
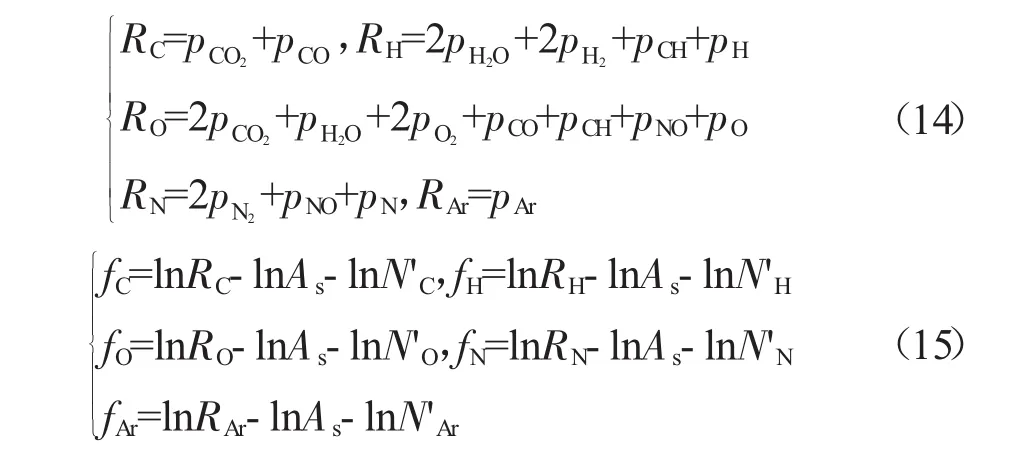
根据式(3)整理成

将式(5)整理成

将式(1)、(3)、(5)以及其中的变量先进行对数处理后,对修正量来说处理后的由式(13)、(16)、(17)构成的方程组是线性的,而对方程组的系数矩阵可以采用高斯主元消去法求解,首先需要给定气体组分分压和As的初值,可以选择按照贫油完全燃烧产物的相应数值给定,这样可以减少迭代次数,但是这样确定初值增加了计算量;可以任意给定1组初值,但是取值不能为0,一般在计算中取氮气的分压初值为0.8 p,其余气体和As的分压初值为10-5p,经过大量抽样计算验证,这种初值取值能满足绝大多数计算工况。经高斯主元消去法得到各修正量并代入式(20)和(21)得到新的各分压值,再将新的数值重新代入系数矩阵中计算,直至相邻2次计算结果满足给定的精度要求为止。在给定精度小于 的情况下,赫夫法的迭代次数在数次到二十几次,该算法的迭代收敛时间要大于双变量迭代法的。
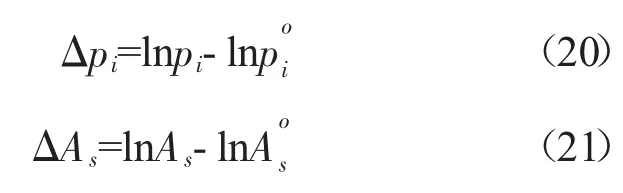
2.3 温度迭代计算
利用双变量迭代法或赫夫法求解化学平衡成分的计算过程实质是在求解由式(1)、(3)、(5)构成的非线性方程组,计算的前提条件是燃烧室工作压力、油气比和燃气温度已知,但是由于计算过程中变量燃气温度是未知的,因此在开始迭代计算时,需要先假定1个燃气温度以便迭代计算。将能量守恒方程式(9)整理为
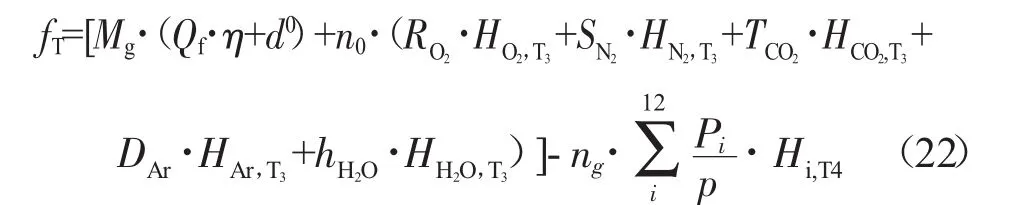
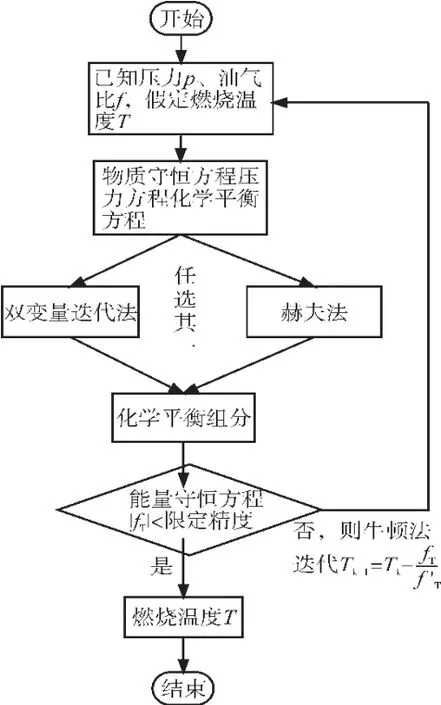
图1 燃气温度的计算流程
式中:fT为温度T的函数。
在计算出燃气平衡成分后,将各成分的物质的量百分数代入式(22),如果|fT|在限定的精度范围内,则结束计算;如果|fT|的值超出限定值,则采用牛顿法迭代公式(23)计算出新的温度,再重新计算化学平衡组分,直至|fT|满足精度要求即可。燃气温度的计算流程如图1所示。

3 算例计算
选用算例对采用双变量同时迭代法、双变量分别迭代法和赫夫法计算得到的燃气平衡组分和燃气温度进行比较分析。设定燃料的氢碳比为1.923,低热值为42650 kJ/kg,进口温度为500℃,燃烧室工作压力为0.5 MPa,按贫油和富油2种情况油气比分别取0.05453和0.07496。采用前面所述的数值解法得到的温度计算结果见表1、2。
从表1、2中结果可得出:
(1)针对同一工作条件,采用数值解法得到的化学平衡组分和燃气温度基本一致;
(2)从计算时间上比较,由快到慢分别为双变量同时迭代法、双变量分别迭代法和赫夫法,但是在燃烧室温度场试验中,测试软件采集数据的频率是1 s采集1组数据,因此任意1种数值解法在测试软件中的应用都满足测试需求;
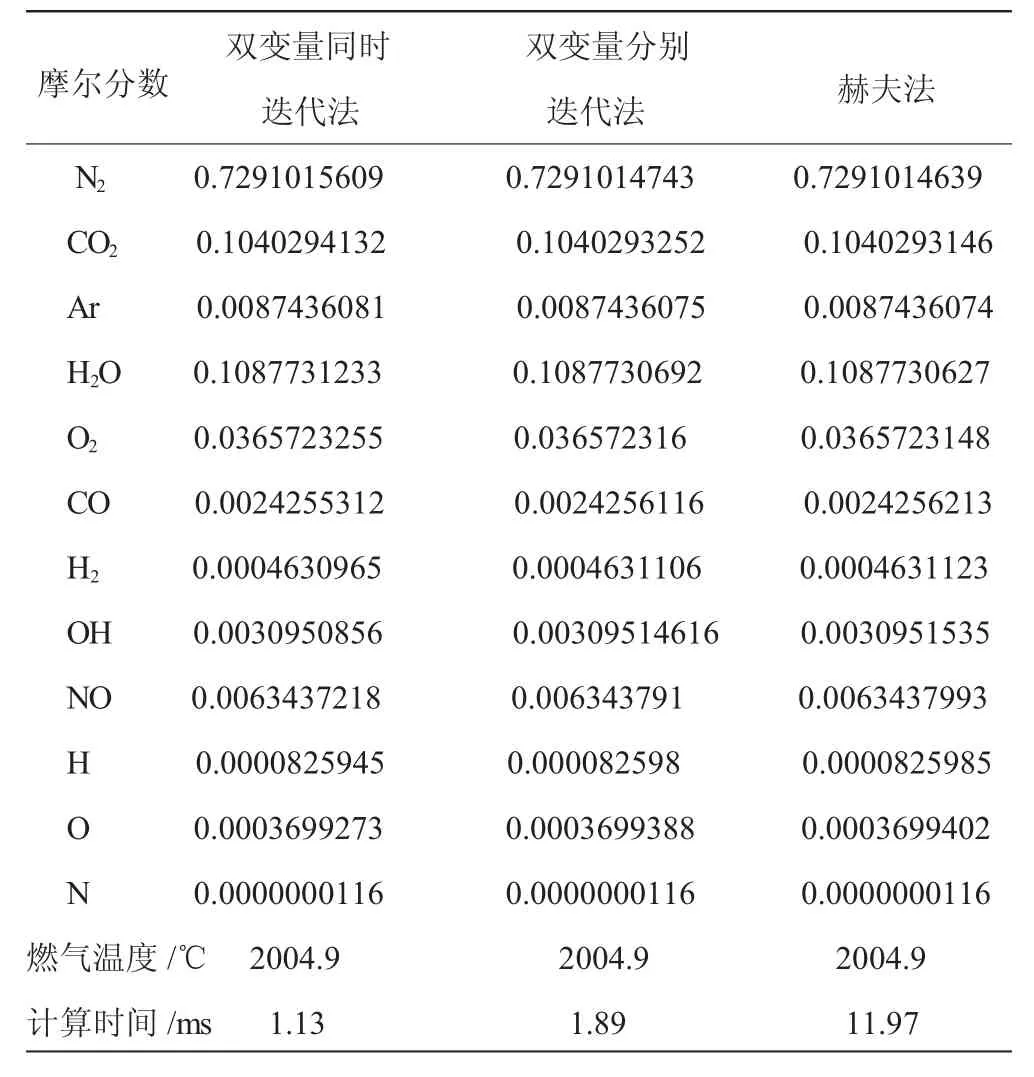
表1 数值解法的结果对比(油气比0.05453)
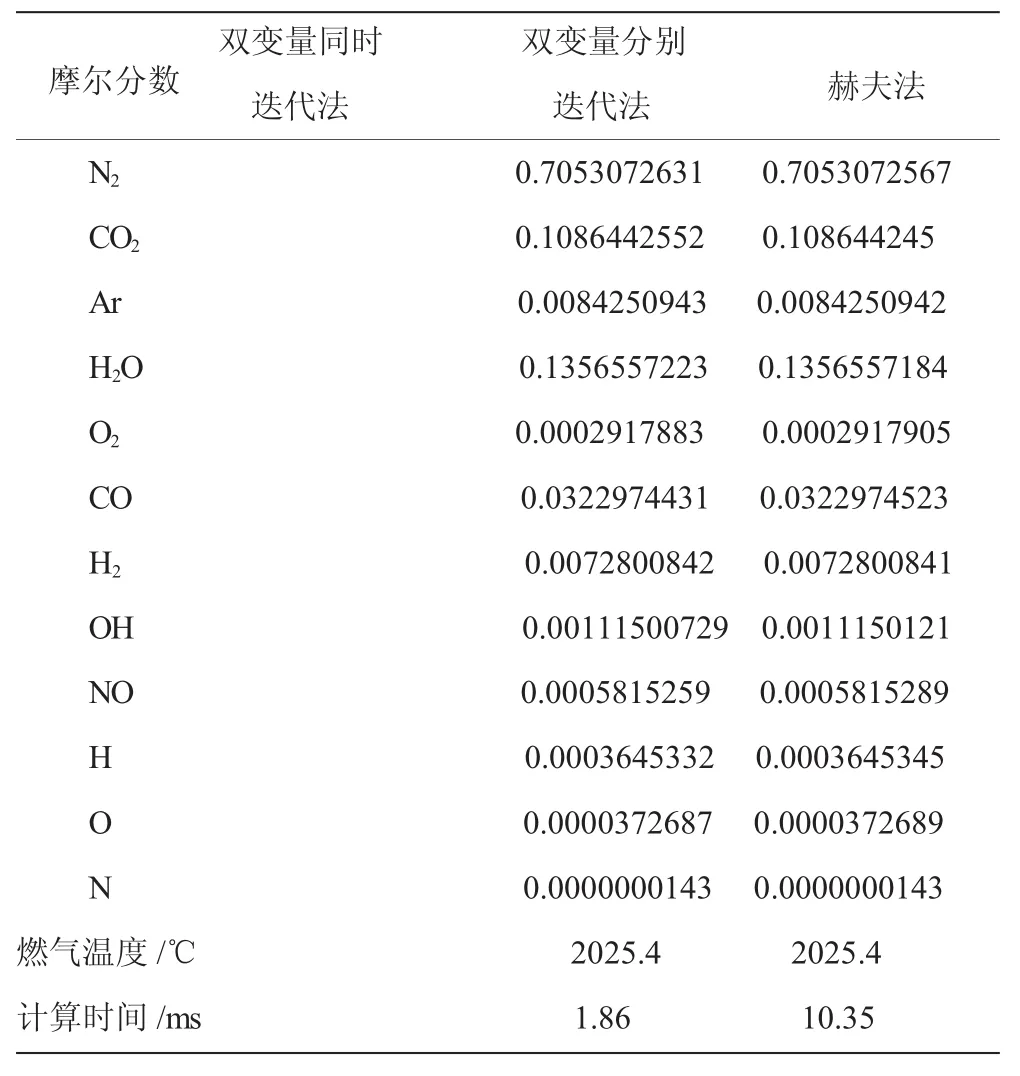
表2 数值解法的结果对比(油气比0.07496)
(3)富油条件下双变量同时迭代法无法完成迭代计算。
在某5头部扇形燃烧室出口温度场试验中,将热电偶与燃气分析的测量结果进行比较。燃烧室采用燃料的氢碳比为1.923,燃料低热值为42650 kJ/kg,进口温度为400℃,工作压力为0.55 MPa,油气比为0.03。燃烧室中间3个头部的热电偶与燃气分析测得的出口温度场结果对比如图2所示,具体数值见表3,其中燃气分析结果包括前面所述采用数值解法得到的温度结果。
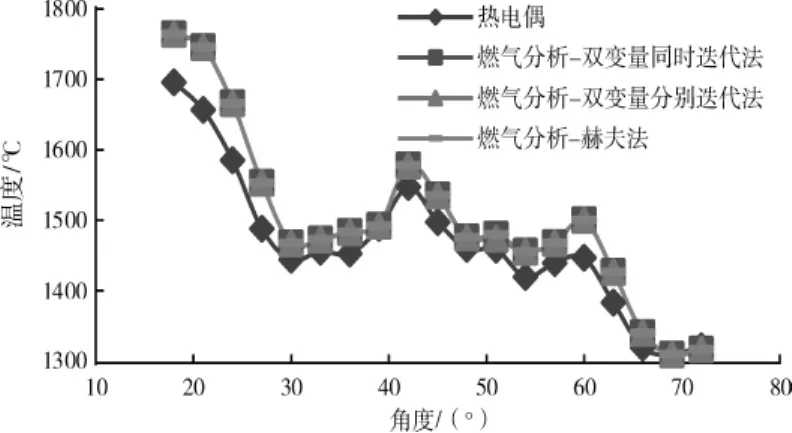
图2 油气比0.03时热电偶与燃气分析温度对比

表3 热电偶与燃气分析温度结果对比
从图2和表3中可见:
(1)热电偶所测温度与燃气分析计算得到的温度沿着周向变化的趋势基本一致,应用双变量迭代法和赫夫法的燃气分析结果相同;
(2)燃气分析的测温结果偏大于热电偶的测温结果,最大相差89℃,最小相差0.4℃,平均相差34.9℃。
4 结论
本文利用双变量迭代法和赫夫法迭代求解用于计算燃气温度的非线性方程组,得出如下结论:
(1)双变量迭代法计算简单,收敛速度快,初值易确定并能满足所有条件下的计算收敛,针对不同的燃烧情况可以采用双变量同时迭代和分别迭代法完成计算。针对贫油燃气,采用双变量同时迭代法收敛更快。
(2)赫夫法是对牛顿-拉夫森法的改进优化,变化后的赫夫法各变量初值几乎可以任意给定,迭代收敛较好并且该方法适用范围非常广,缺点是每次迭代都需要重新计算1次系数矩阵,计算量较大。
(3)通过算例验证可知,所有数值解法得到的计算结果基本一致,但从计算迭代收敛的速度来看,双变量同时迭代法计算最快,赫夫法计算相对较慢。
(4)针对某5头部扇形燃烧室中间3个头部出口温度的对比结果可见,燃气分析计算得到的温度大于热电偶测得的温度。
