求解线性互补问题的一类矩阵分裂迭代算法
2022-07-04王爽,唐嘉
王 爽,唐 嘉
求解线性互补问题的一类矩阵分裂迭代算法
王 爽,*唐 嘉
(福建师范大学数学与统计学院,福建,福州 350007)
通过改进 NMMS 方法,建立了一类新的基于模的两步矩阵分裂 (NTMMS) 迭代法,给出了该算法在适当条件下的收敛性,包括加速超松弛分裂的情况。数值实验表明,该方法在实际应用中优于传统的迭代法。
线性互补问题;矩阵分裂;迭代法;收敛性
0 引言

为了在实际计算中更灵活地求解LCP,通常使用矩阵分裂来构造有效的迭代方法, 如投影松弛迭代法[2],一般的不动点迭代法[3],和矩阵多重分裂迭代法[4]。最近,基于线性互补问题的等价不动点形式,吴在文献[5]给出了如下等价形式:

本文旨在进一步加速LCP的一类新的基于模的矩阵分裂 (NMMS) 迭代法。为了达到更高的计算效率,并充分利用系数矩阵中包含的信息,对LCP采用了两步分裂技术,因此,我们提出了一类新的基于模的两步矩阵分裂 (NTMMS) 迭代法。在适当选择矩阵分裂的情况下,这类新方法可以产生一系列松弛形式。此外,还讨论了该方法的收敛性,并在适当的假设下给出它的一些收敛条件。数值实验表明,所提出来的方法优于现有的方法。
本文的其余部分组织如下:在第1节中,陈述了一些预备知识;在第2节中,我们提出了一类新的基于模的两步矩阵分裂迭代法来求解LCP;在第3节中,给出了该方法的收敛性分析,包括加速超松弛分裂的情况;在第4节中,给出一个数值算例;在第5节中,对本文的工作进行了总结。
1 预备知识
在本节中,简要地介绍一些符号,初步定义和必要的引理,以便在后续讨论中使用。
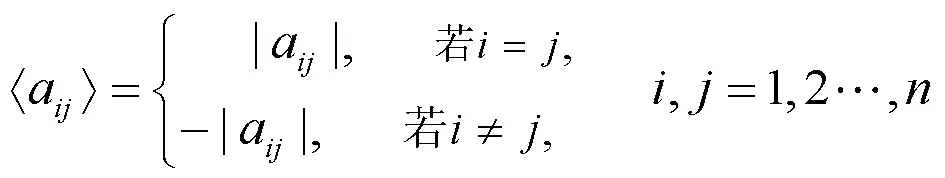
然后,给出了在后续中有用的一些引理。




2 一类新的基于模的两步迭代法
算法1(用于求解LCP的NTMMS迭代法)


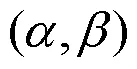
3 收敛性分析
在本节中,给出了确保在适当条件下算法1收敛的几个充分条件。首先,我们给出了算法1的一般收敛性条件,见定理1。
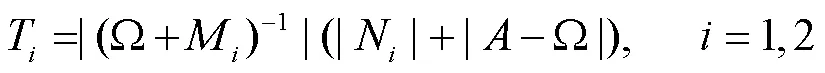


在(5)中,对第一个方程的左右两边同时取绝对值,可以得到
同样,由(5)式中的第二个方程可以得到
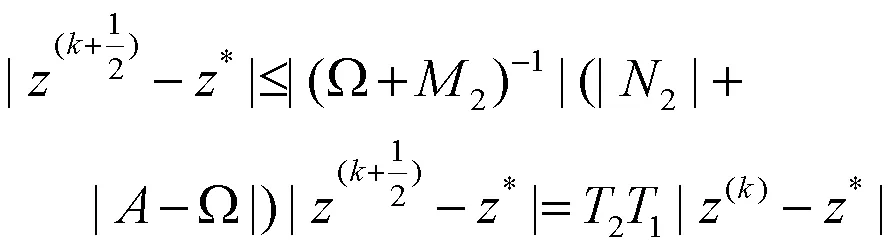
因为
且

从而有


同样,有


成立。因此

基于上述结果,取

那么
类似地,有

所以,
4 数值实验
本节给出一个数值例子说明所提出的算法1的有效性。数值结果从三个方面进行分析:迭代步骤 (以“IT”来表示)、以秒为单位的运行时间(以“CPU”来表示)和绝对残差向量范数 (以“RES”来表示)。在这里,




是LCP的唯一解。
3)数值实验表明,NTMSOR迭代法相比较NMSOR迭代法需要更少的迭代步数和CPU时间。这表明,当这两种方法被用于求解LCP时,NTMSOR迭代法是优于NMSOR迭代法。
表1 算例1的数值结果
Table 1 Numerical results of example 1
mNMSORNTMSOR ITCPURESITCPURES 2203040506026272829290.05180.16140.43401.00421.99936.4949e-067.3283e-066.1384e-068.2741e-065.7451e-0615151616160.04890.17120.46561.14452.16554.1632e-069.2305e-064.9328e-066.7204e-068.5076e-06 4203040506017181818190.04240.11640.30280.69621.37416.8128e-064.5957e-066.6315e-068.6670e-064.0932e-0610101010110.03470.11720.31810.76001.56702.4588e-064.5437e-066.6268e-068.7093e-061.9127e-06 6203040506014141515150.03470.10370.26180.57681.10424.5747e-067.8387e-063.2373e-064.1969e-065.1565e-06888880.03250.09910.26780.62171.20012.2640e-063.9763e-065.6877e-067.3987e-069.1096e-06
5 结论
本文建立了一类新的基于模的两步矩阵分裂迭代法,研究了该方法的收敛性,在适当条件下给出了保证该方法收敛的充分条件。数值实验表明,该方法在迭代步数和CPU时间方面均优于现有的方法。此外,选择不同的参数对计算结果有着显著的影响。然而,在一般情况下很难找到其最优参数,因此,理论上研究最优参数的选取将是一个值得研究的课题。
[1] Cottle R W, Dantzig G B. Complementary pivot theory of mathematical programming[J]. Mathematics of the decision sciences, part, 1968, 1(1):103-125.
[2] Bai Z Z.On the monotone convergence of the projected iteration methods for linear complementarity problems[J].Numerical Mathematics Theory Methods and Applications, 1996,5(2): 228-233.
[3] Hu J G. Scaling transformation and convergence of splittings of matrix[J]. Math. Numer. Sinica,1983,5(1):72-78.
[4] Bai Z, Huang Y. A class of asynchronous parallel multisplitting relaxation methods for large sparse linear complementarity problems[J]. Journal of Computational Mathematics, 2003(6): 773-790.
[5] Wu S, Li C. A class of new modulus-based matrix splitting methods for linear complementarity problem[J]. Optimization Letters, 2021,16:1427-1443.
[6] Bai Z Z. Modulus-based matrix splitting iteration methods for linear complementarity problems[J]. Numerical Linear Algebra with Applications, 2010, 17(6): 917-933.
[7] Ma C, Huang N. Modified modulus-based matrix splitting algorithms for a class of weakly nondifferentiable nonlinear complementarity problems[J]. Applied Numerical Mathematics, 2016, 108: 116-124.
[8] Hong J T, Li C L. Modulus-based matrix splitting iteration methods for a class of implicit complementarity problems[J]. Numerical Linear Algebra with Applications, 2016, 23(4): 629-641.
[9] Wu S L, Guo P. Modulus-based matrix splitting algorithms for the quasi-complementarity problems[J]. Applied Numerical Mathematics, 2018, 132: 127-137.
[10] Mezzadri F, Galligani E. Modulus-based matrix splitting methods for horizontal linear complementarity problems[J]. Numerical Algorithms,2020, 83(1): 201-219.
[11] Bai Z Z, Zhang L L. Modulus-based synchronous two-stage multisplitting iteration methods for linear complementarity problems[J]. Numerical Algorithms, 2013, 62(1): 59-77.
A CLASS OF MATRIX SPLITTING METHODS FOR LINEAR COMPLEMENTARITY PROBLEMS
WANG Shuang,*TANG Jia
(School of Mathematics and Statistics, Fujian Normal University, Fuzhou, Fujian 350007, China)
By improving the NMMS method, a class of new two-step modulus-based matrix splitting methods are established in this paper. The convergence of the algorithm under appropriate conditions is given, including the case of accelerated overrelaxation splitting. Numerical experiments show that the proposed method is superior to some existing methods in actual implementation.
linear complementarity problem; matrix splitting; iteration method; convergence
1674-8085(2022)04-0001-06
O241.6
A
10.3969/j.issn.1674-8085.2022.04.001
2022-03-18;
2022-04-15
国家自然科学基金青年基金项目(11901024),福建省自然科学基金面上项目(2020J01166,2021J01661).
王 爽(1996-),女,陕西渭南人,硕士生,主要从事数值代数方面研究(E-mail: ws2811814571@163.com);
*唐 嘉(1983-),女,湖南湘潭人,副教授,博士,主要从事数值代数及其应用研究(E-mail: tang_jia@126.com).
