考虑航空发动机支承不同心的整机动力学建模及分析

吴英祥，张亚双，陈 果

（1.中国航发沈阳发动机研究所，沈阳110015；2.中国航发沈阳黎明航空发动机有限责任公司，沈阳110043；3.南京航空航天大学民航学院，南京210016）

0 引言

同心度是对航空发动机整机振动响应有重要影响的参数，在发动机装配过程中，必须进行严格控制[1]。航空发动机不同心主要包括转子、支承和转静子不同心[2]。转子不同心将引发较大的不平衡响应，转静子不同心可能引发碰摩故障，二者的故障机理比较清楚，但是支承不同心故障机理尚不清楚。张振波等[3]建立了适应航空发动机柔性转子系统在不同心和不平衡激励作用下的动力学模型，研究了带有支承不同心的转子动力学响应问题。冯国全等[4]基于某航空发动机转子系统，建立了考虑支撑轴承不对中的内外双转子系统动力学模型，分析了低于和高于第1阶临界转速的情况，结果表明，内外转子的振动均出现2倍频成分，且随着不对中程度的加大，2倍频成分也明显增大且会占主导，轴心轨迹会从近似圆形变化为8字形。Xu M等[5-6]分析了柔性电机的不对中和不平衡故障机理，并采用试验方法进行了验证。Al-Hussain K M[7]和Lees A W[8]研究了刚性联轴器的不对中故障特性。李明[9]建立了1个平行不对中转子系统的动力学模型，研究了平行不对中转子系统的非线性动力学特性。长期以来，人们普遍认为支承不同心将引发转子不对中，导致用联轴器连接的2个转子形成平行不对中和角度不对中，最终在联轴器两端形成附加力和力矩，从而引发转子系统振动，进而对发动机整机振动产生影响，并且认为不对中故障的特征之一是出现较大的2倍频[10]。在航空发动机实际工作中，支承不同心基本控制在数十微米，可以通过轴承间隙来补偿，装配完成后不会产生较大的附加力矩；但如果控制不严格，数十微米的支承不同心也会产生较大的整机振动和轴承损坏。现有的转子不对中和轴承不对中模型难于解释数十微米支承不同心所引发的整机振动问题。

因此，深入研究支承不同心对航空发动机整机振动的影响机理及有效控制发动机整机振动具有重要意义。本文将支承不同心转化为轴承间隙，并将模型导入整机模型进行耦合动力学仿真，研究了由于支承不同心所引发的整机振动问题，并以某型双转子涡扇航空发动机为例进行仿真分析。

1 支承不同心模型

支承不同心的纵剖面和横截面模型如图1所示。图1（b）为支承不同心下的滚动轴承作用力模型，其中O1为支承原始中心，O2为支承不同心后的支承处转子轴心。设：c为轴承间隙，xr、yr分别为转轴的x向和y向位移，xB、yB分别为轴承座的x向和y向位移，x0、y0分别为支承x向和y向的不同心量。位移r为转轴与轴承间的径向相对位移，其表达式为

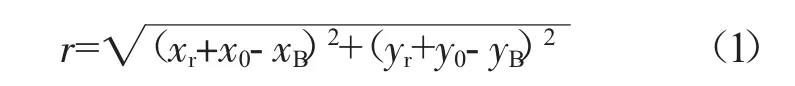
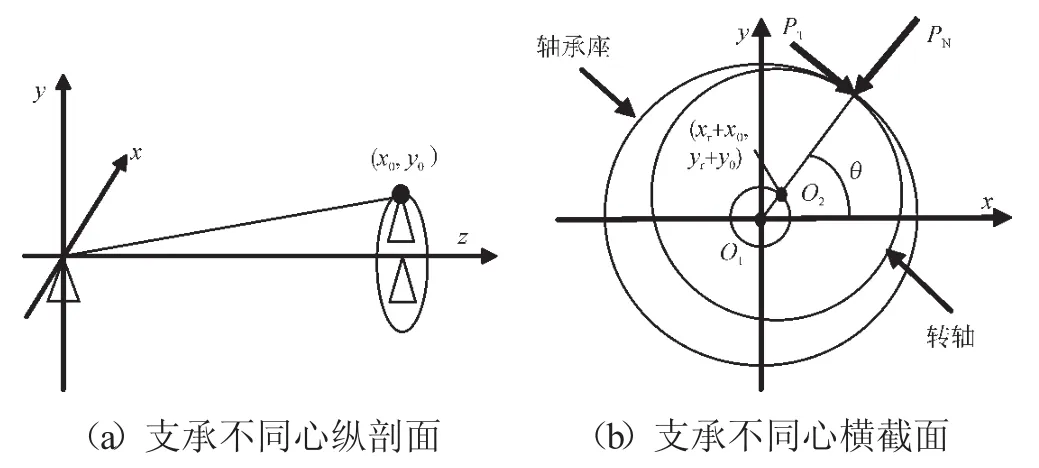
图1 支承不同心模型

当r＜c时，不发生接触；当r≥c时，发生接触。假设摩擦符合库仑摩擦定律，则轴承接触后产生的法向力和切向力摩擦力为

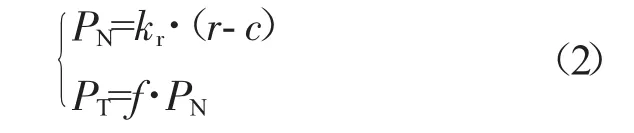
式中：kr为轴承径向刚度；f为摩擦系数。需要注意的是，切向摩擦力需要根据轴承外圈和轴承座之间的相对运动速度方向来判断。将法向和切向作用力分解在x轴和y轴

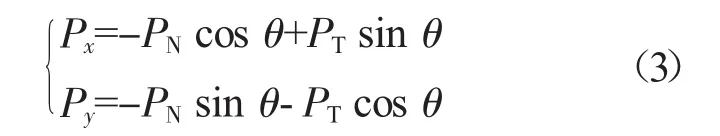
另外，滚动轴承外圈通常需要利用锁紧螺母锁紧。在拧紧螺母压力作用下，当外圈与轴承座存在相对运动时，外圈与锁紧螺母内表面将产生摩擦效应，该摩擦效应主要表现为干摩擦阻尼效应，而轴承拧紧力矩将改变接触面间的摩擦力，从而改变摩擦阻尼，不失一般性，为了简化研究，本文将摩擦阻尼等效为黏性阻尼。

2 发动机支承不同心建模分析

某型双转子航空涡扇发动机支承形式如图2所示。从图中可见，该型发动机低压转子采用1-2-1型支承方式，支承1位于低压压气机之前，支承2、3位于低压压气机和低压涡轮之间，支承5位于低压涡轮之后。低压压气机转子与低压涡轮转子采用柔性联轴器联接，传递扭矩和轴向力。高压转子采用1-0-1型支承方式，支承3位于高压压气机之前，支承5位于高压涡轮之后。

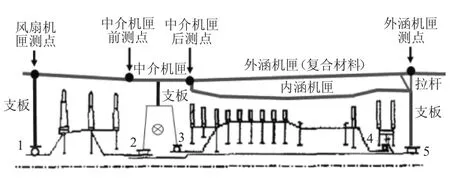
图2 某型双转子航空发动机支承结构

对于该转子系统，支承1、2支承低压压气机转子，位于风扇前后，跨度较短，且均支承在同一段机匣上，其同心度易于保证。支承5位于低压涡轮之后，跨度较大，且支承5处于高温环境中，其同心度往往很难保证。高压转子后支承为中介轴承支承（图2中的支点4），支承在低压转子上，因此，高压转子支承的同心度需要通过支承3、5的同心度反映。综上所述，在该型发动机上重点关注的支承不同心主要为：支点2、5，其不同心模型如图 3所示；支点 3、5，其不同心模型如图4所示。

图3 低压转子支承2-5的不同心度模型

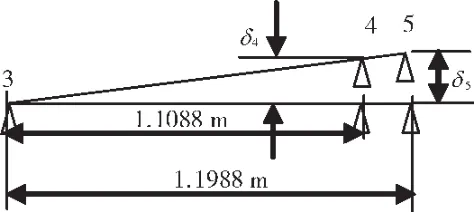
图4 高压转子支承3-5的不同心度模型

从图3中可见，当低压转子支点12-5不同心时，支点5的不同心量为δ5，则支点4对应的内转子不同心量为δ4。支点4和5的距离很近，在低压转子支承2-5不同心模型中，δ4=0.93δ5；在高压转子支承 3-5不同心模型中，δ4=0.92δ5。

在出现低压转子支承2-5不同心（图3）和高压转子支承3-5不同心（图4）时，为了能够实现高、低压转子的装配，必须要调整支点4和5的滚动轴承径向间隙，否则，转子将承受由不同心产生的附加力矩，从而使转子产生初始弯曲变形。事实上，由于航空发动机是高精度旋转机械，其不同心量很小，通过调整滚动轴承间隙即可实现不同心量的补偿。在该假设前提下，显然不同心量的大小将直接影响滚动轴承间隙的大小，而航空发动机支承不同心下的整机振动响应和轴承载荷也与滚动轴承间隙大小息息相关。

本文通过数值仿真计算来分析低压转子支承2-5不同心度和高压转子支承3-5的不同心度对航空发动机整机振动的影响。在同心度模型中，将不同心度等效为支点4、5的滚动轴承间隙。

3 含支承不同心的发动机整机振动建模

3.1 发动机整机振动模型

航空发动机整机振动建模包括转子系统有限元模型、机匣有限元模型、支承集总参数模型，是混合动力学模型，该方法运用Newmark-b法和翟方法相结合进行时域数值积分求解，可以高效地求解系统非线性响应[11-12]。

3.1.1 转子系统运动方程

将转子考虑为由若干支承和转盘组成的系统。转子利用有限元方法离散为普通梁单元，考虑转子系统的剪切变形、陀螺力矩和转动惯量。将单元的运动方程进行组装，得到转子系统运动方程

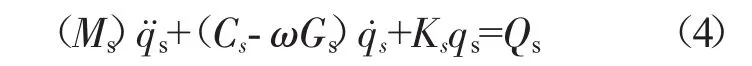
式中：Qs为系统广义外力向量；Ms为系统质量矩阵；Gs为系统陀螺矩阵；Ks为系统刚度矩阵；Cs为系统阻尼矩阵，本文将Cs假设为比例阻尼。

3.1.2 机匣运动方程

将机匣按不旋转的轴（梁单元结构）处理，也需考虑剪切效应和转动惯量。因此，与转子模型的处理方法相同，用有限元方法得到机匣的运动微分方程

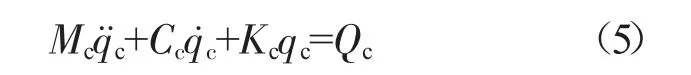
式中：Qc为机匣系统广义外力向量；Mc为机匣系统质量矩阵；Kc为机匣系统刚度矩阵；Cc为机匣系统阻尼矩阵，同样假设Cc为比例阻尼。

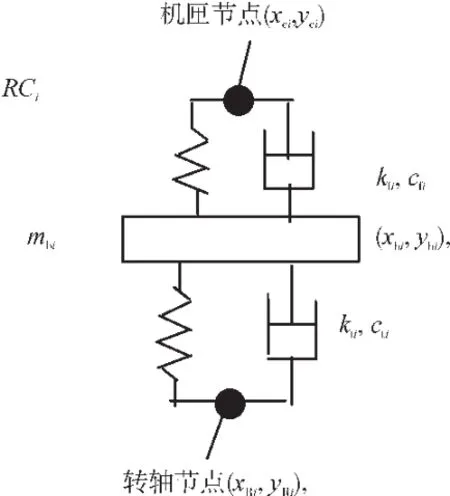
图5 转子-机匣支承

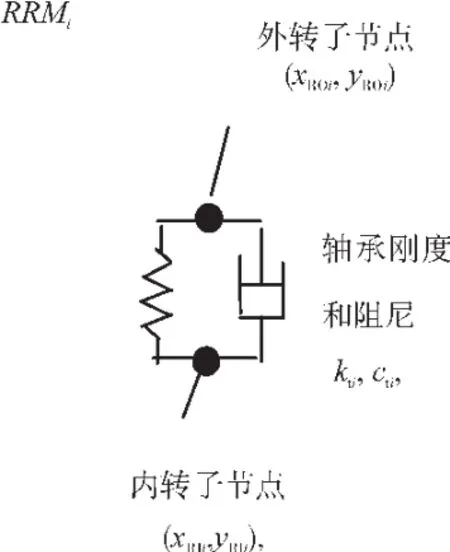
图6 中介轴承支承

3.1.3 转子-机匣间的支承连接

对于每个转子与机匣间的支承RCi（i=1，2，…，N），包括滚动轴承、轴承座等部件，滚动轴承用线性弹簧模拟。其中，mbi为轴承座质量；kti为转轴与轴承座之间的轴承弹性支承刚度，cti为对应的阻尼系数；kfi，cfi分别为机匣与轴承座之间的支承刚度和阻尼，如图5所示。从图中可见，kti为转轴与轴承座之间的轴承等效刚度，由于支承不同心引起了轴承间隙的变化，因此轴承力表现为类似于转静碰摩的碰摩力。设轴承间隙为c，支承不同心量为x0和y0。转子-机匣间的支承力（即支承RCi作用于转子的力）为

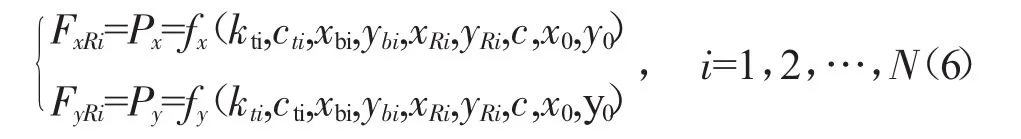
设机匣节点位移为xci和yci，支承RCi的轴承座的位移为xbi和ybi，则机匣作用于支承RCi的力为

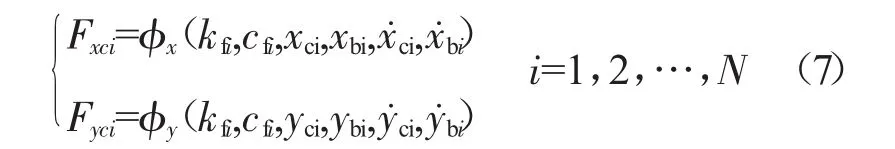
因此，支承RCi的轴承座的运动微分方程为

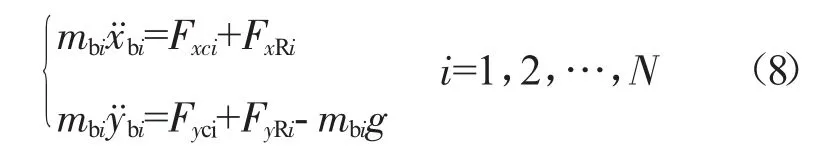
3.1.4 转子-转子间的中介轴承支承

对于每个转子与转子间的中介轴承支承RRMi（i=1，2，…，N），仅仅包括滚动轴承的支承刚度，如图6所示。从图中可见，kti为转轴与轴承座之间的轴承等效刚度，由于支承不同心引起轴承间隙的变化，因此轴承力类似于转静碰摩的碰摩力。设轴承间隙为c，支承不同心量为x0和y0。转子-转子间的中介轴承支承力（即支承RRMi作用于内外转子的力）为

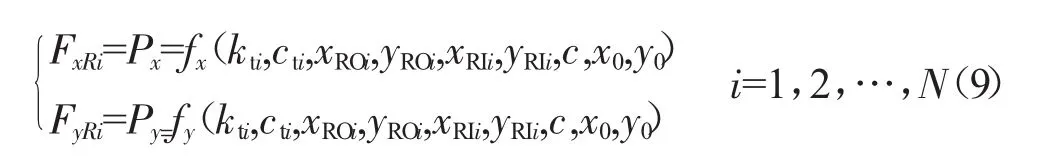
3.2 支承不同心的航空发动机整机振动分析

3.2.1 计算条件

3.2.1.1 高、低压转速变化关系

（1）低压转速 N1=0～3552 r/min，高压转速 N2=3N1；（2）N1=3552～8880 r/min，N2=0.77121N1+7826.6621。

3.2.1.2 不平衡量

考虑实际发动机的不平衡量分布：（1）第1、3级风扇叶片不平衡量为 100 g·cm；（2）第 4、9 级高压压气机叶片不平衡量为127 g·cm；（3）第9级高压压气机盘后1节点（蓖齿盘）和高压涡轮叶片后1节点（修正面）不平衡量为 120 g·cm；（4）第 1、2 级低压涡轮叶片不平衡量为250 g·cm。

3.2.1.3 不同心计算条件

不同心的计算条件见表1。考虑正常同心度的工况Case1下，滚动轴承的径向间隙均设定为0 μm。在较大不同心度的工况Case2下，设定支点5轴承间隙为50 μm，支点4中介轴承间隙为45 μm。在更大不同心度的工况Case3下，设定支点5轴承间隙为100 μm，支点4中介轴承间隙为90 μm。

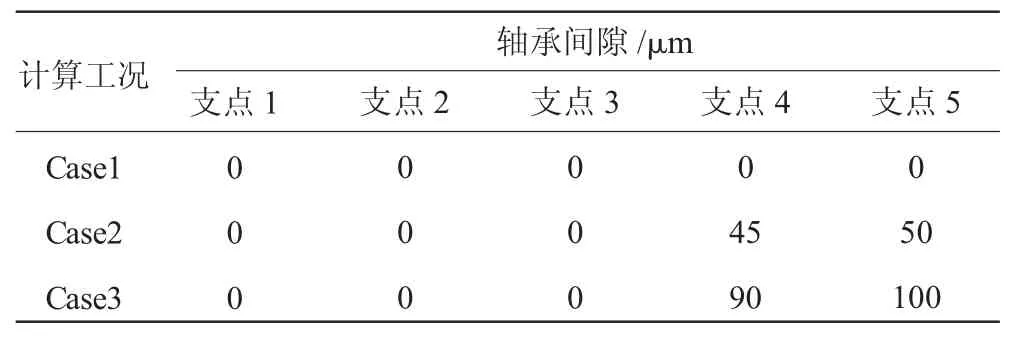
表1 支承不同心的计算工况

3.2.2 支承不同心的影响分析

分别对3种工况进行仿真计算，支承1、2、4、5处的轴承力和转子节点的振动加速度的最大值比较分别如图7、8所示，计算结果分别见表2、3；进气机匣、中介前机匣、中介后机匣、涡轮机匣测点对应的节点力和振动加速度的最大值比较分别如图9、10所示，计算结果分别见表4、5。

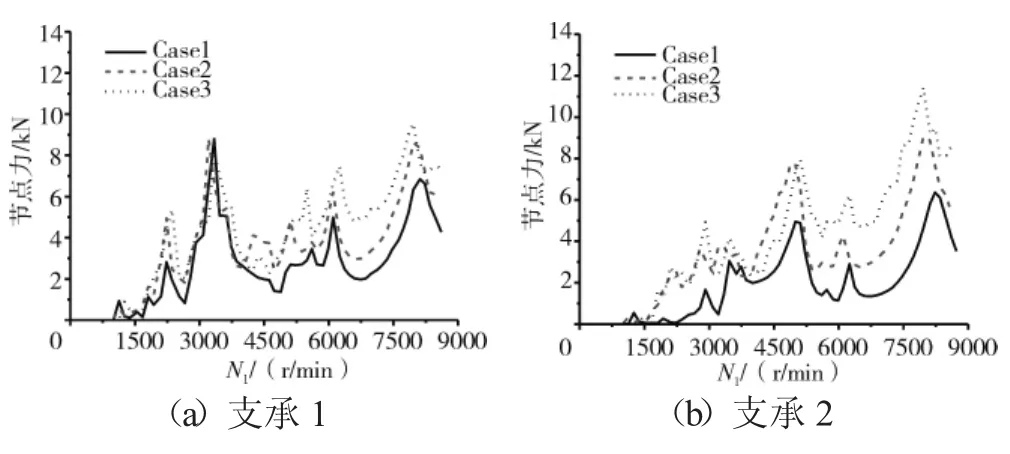
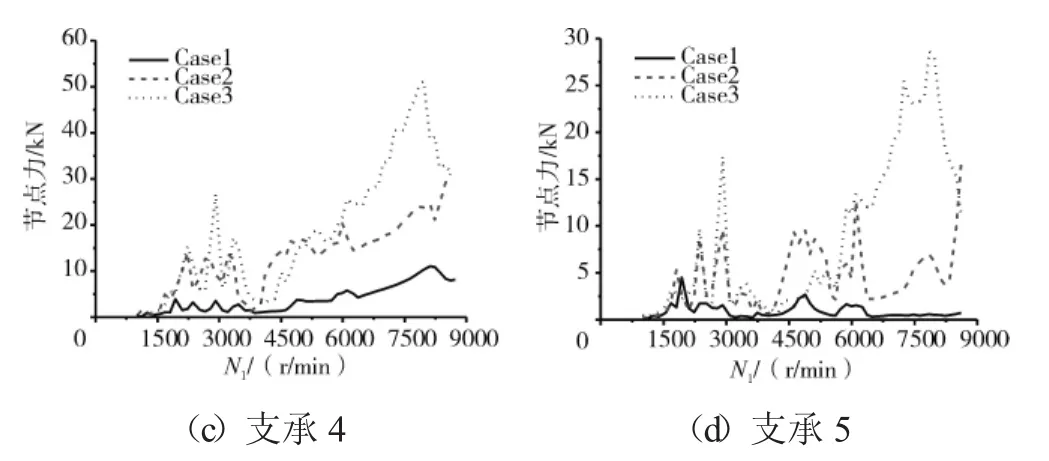
图7 支承处转子节点的轴承作用力

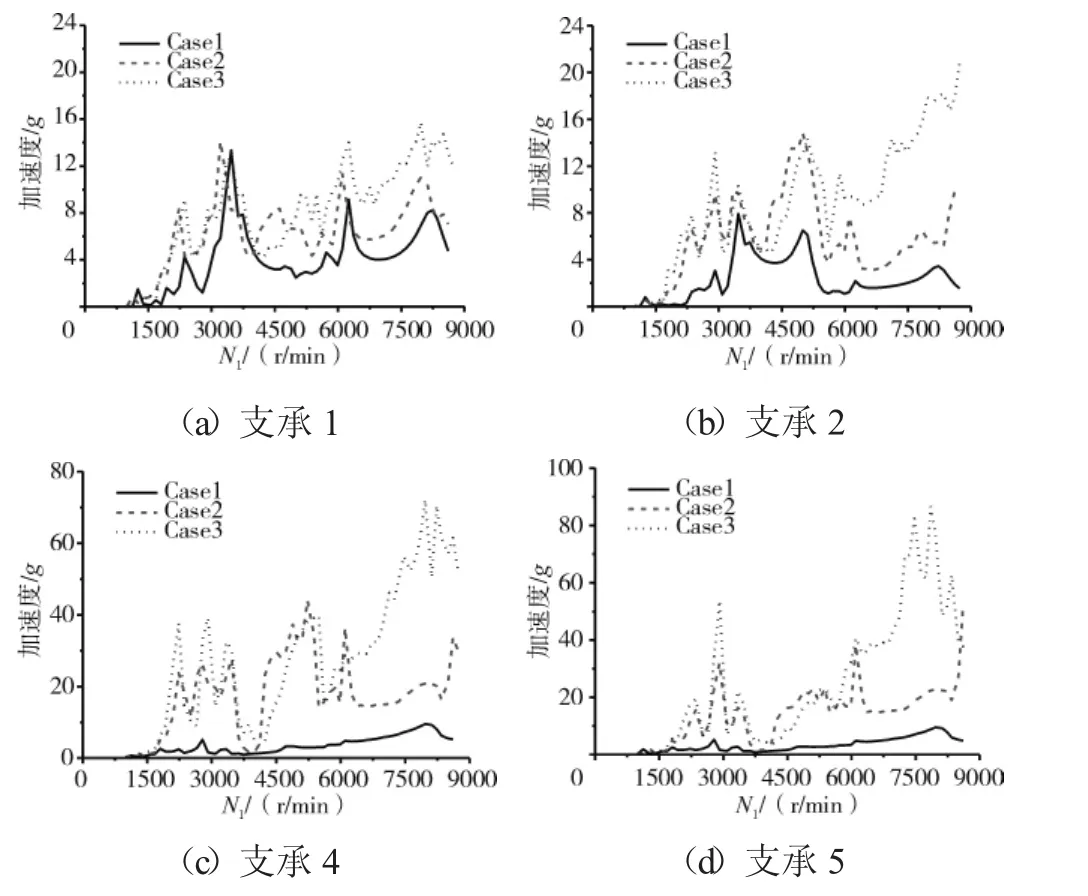
图8 支承处转子节点的振动加速度

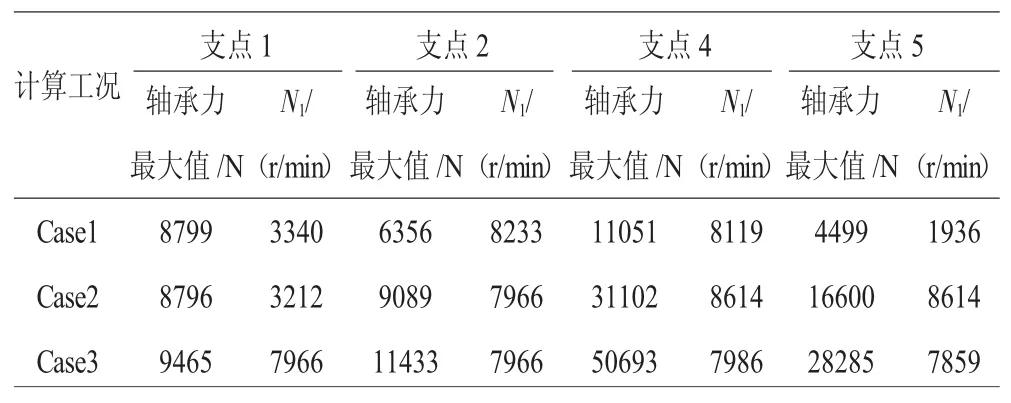
表2 支承轴承力计算结果比较

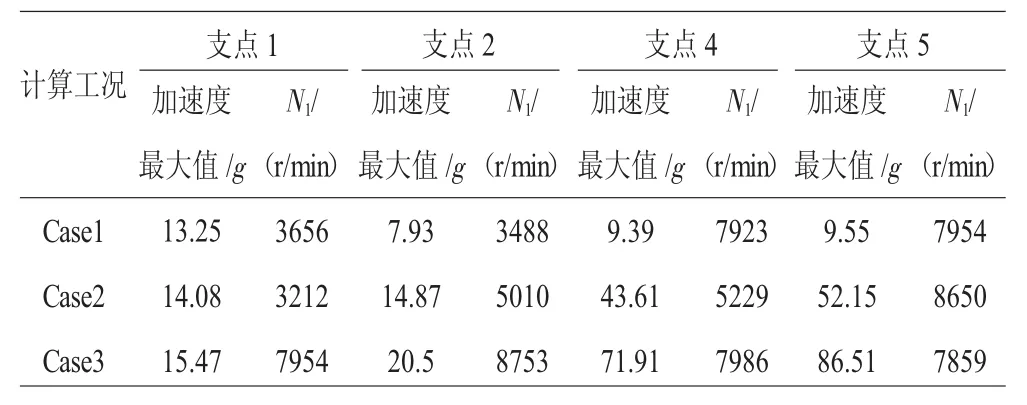
表3 支承处转子节点加速度计算结果比较

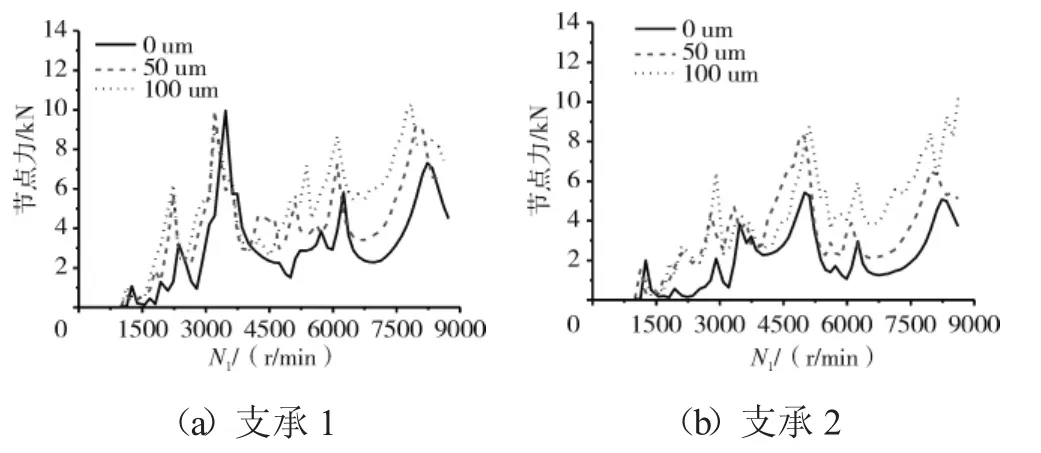
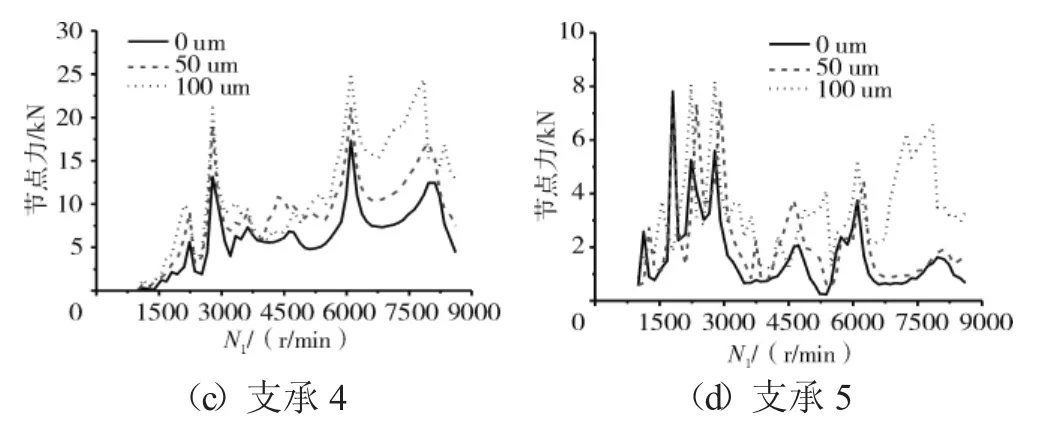
图9 机匣测点对应的机匣节点力最大值随N1的变化规律

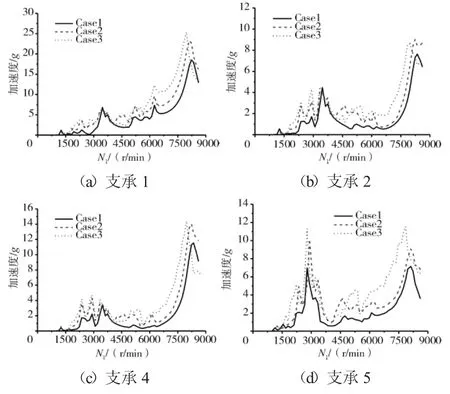
图10 机匣测点加速度最大值随转速N1的变化规律

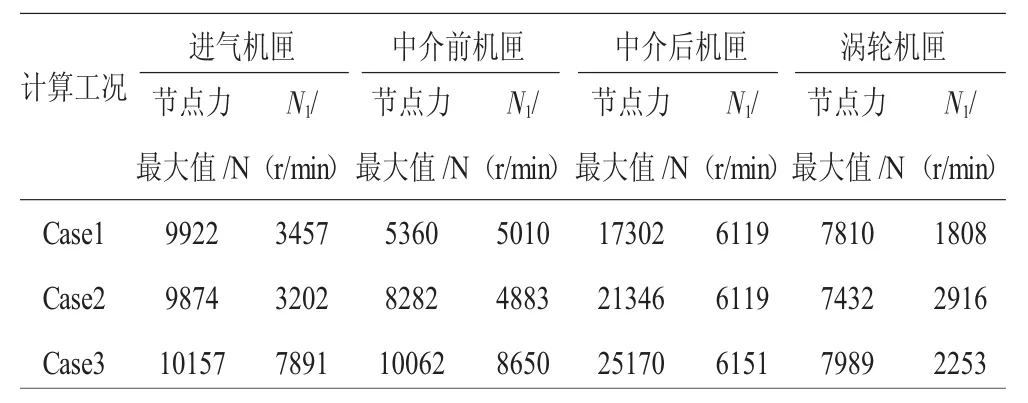
表4 机匣测点对应的机匣节点力计算结果比较

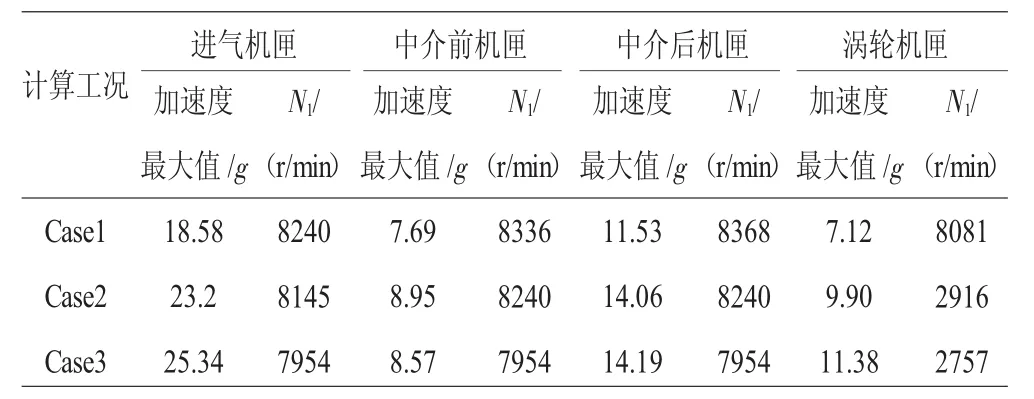
表5 机匣测点加速度计算结果比较

从图7和表2中可见，支点4处的轴承力最大值，在Case1完全同心时仅为10 kN，随着不同心度的增加，在中度Case2的不同心时达到30 kN，而在Case3的严重不同心时达到50 kN。支点5处的轴承力最大值，在Case1完全同心时仅为5 kN，在Case2时达到15 kN，而在Case3时达到30 kN。对于支承1和2，不同心度对其影响很小，轴承力随着不同心的加剧增加不大。

从图8和表3中可见，支点4处的转子节点的振动加速度最大值，在Case1完全同心时仅为10g，随着不同心度的增加，在Case2时达到40g，在Case3时达到70g。支点5处的转子节点加速度最大值，在Case1时仅为10g，在Case2时达到40g，在Case3时达到90g。支承1、2对应的支承转子节点振动加速度随着不同心的加剧增加不大。

从图9、10和表3、4中可见，随着不同心的加剧，机匣测点的响应加速度和机匣节点力增加并不大，表明由不同心引发的轴承力传递到机匣时已经衰减许多，所以机匣测点加速度对不同心故障并不灵敏。

由此可见，过大的不同心尽管引起的机匣加速度并不大，但是导致轴承力很大，从而引起轴承加速磨损、疲劳破坏。其中支承不同心对中介轴承影响最大，这也是航空发动机中介轴承最容易损坏的原因之一。

不同支承不同心情况下支承4、5处的轴承力3维瀑布图分别如图11～13所示。从图中可见，支承不同心引起了更多的倍频特征，并出现了“连续”谱特征，表明过多过大的轴承间隙引起系统的运动不稳定，表现出混沌特征。

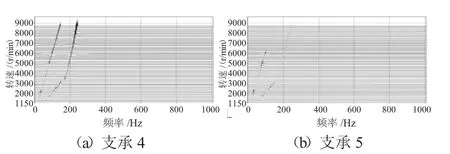
图11 Case1下的支承轴承力3维瀑布图

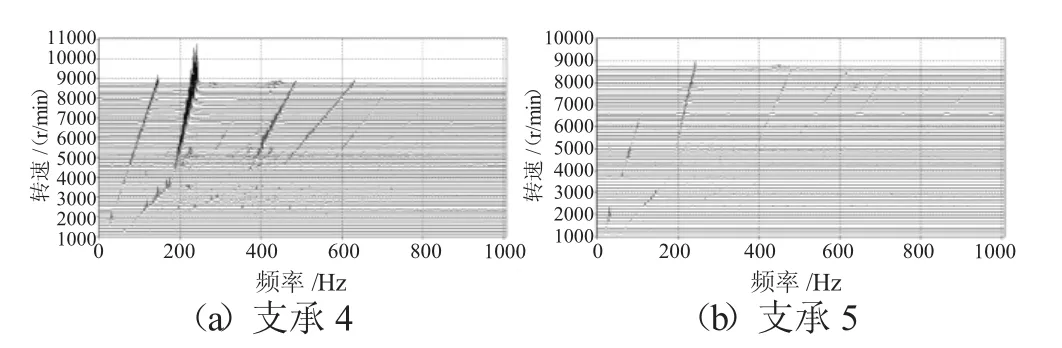
图12 Case2下的支承轴承力3维瀑布图

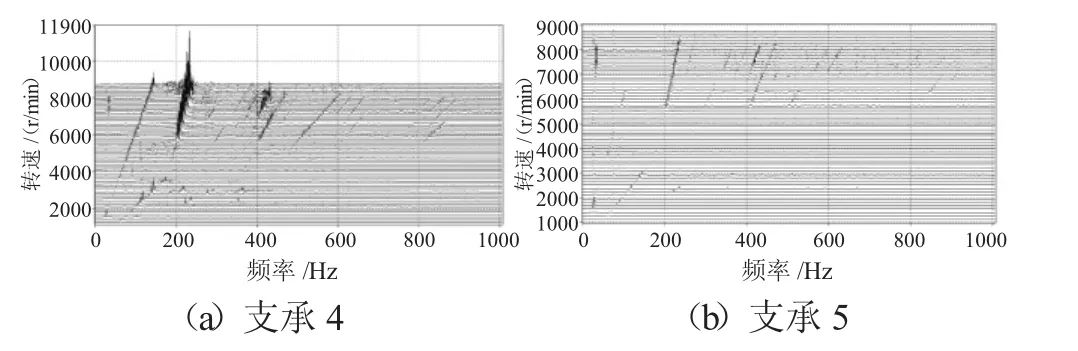
图13 Case3下的支承轴承力3维瀑布图

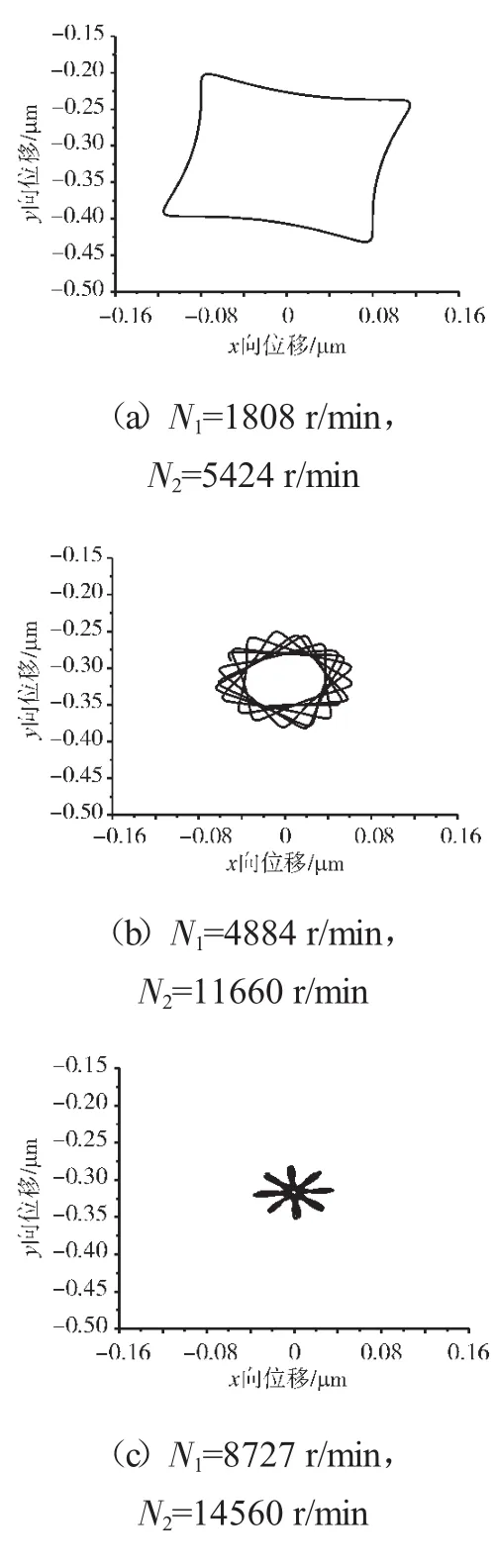
图14 支承不同心Case1情况下的支承4低压转子节点轴心轨迹

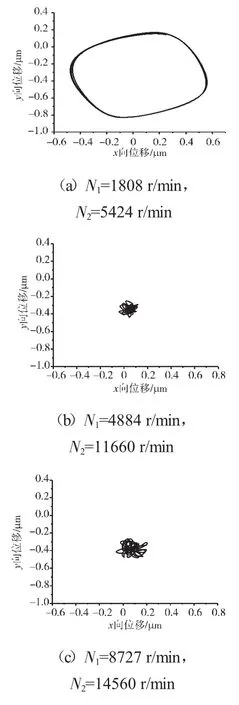
图15 支承不同心Case2情况下的支承4低压转子节点轴心轨迹

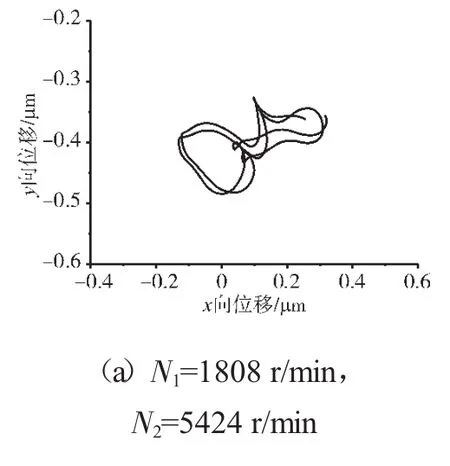
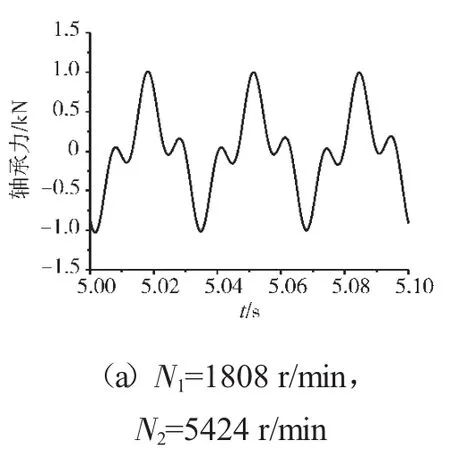
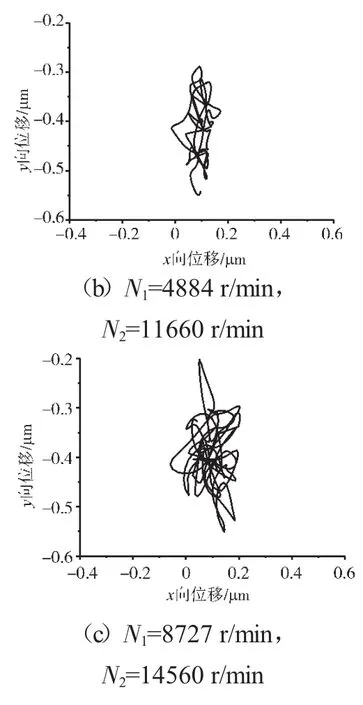
图16 支承不同心Case3情况下的支承4低压转子节点轴心轨迹

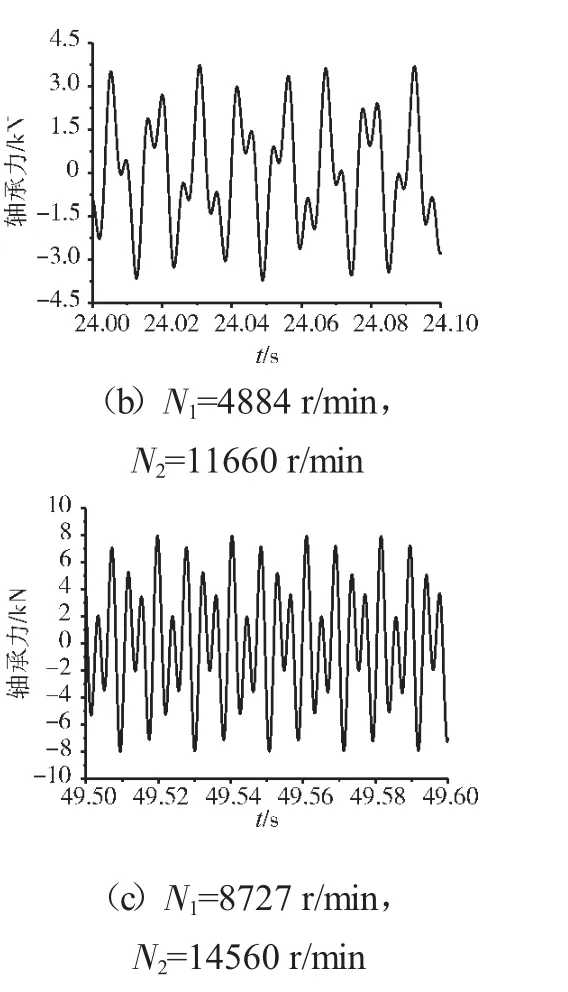
图17 支承不同心Case1情况下的支承4轴承力时域波形

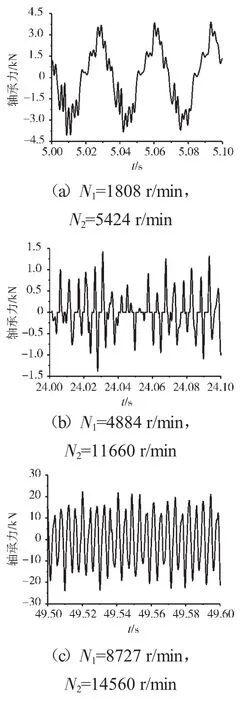
图18 支承不同心Case2情况下的支承4轴承力时域波形

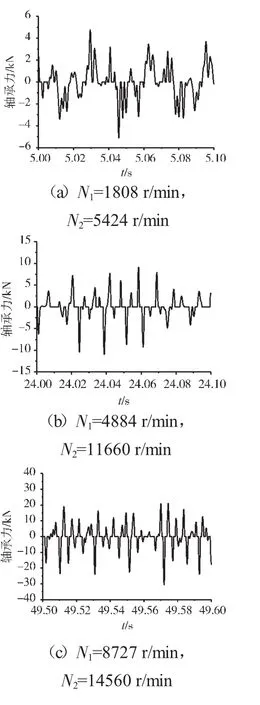
图19 支承不同心Case3情况下的支承4轴承力时域波形

支承不同心Case1、Case2和Case3下的支承4处低压转子节点的轴心轨迹、对应低压转子节点的振动加速度时域波形和频谱分别如图14～22所示。从图中可见，在Case1情况下，由于不存在轴承间隙，系统为线性系统，因而轴承力表现为高低压转速频率的组合。这种组合根据高低压转速的频率比值不同而出现不同形状的很规则的轴心轨迹；在Case2情况下，由于存在轴承间隙，系统表现为非线性特征，轴承力除了高低压转速频率以外还有其他倍频和“连续”谱成分。这种频率成分复杂的组合导致轴心轨迹较为紊乱；在Case3情况下，不同心度更大，轴承间隙也更大，系统非线性特征更加强烈，轴承力的“连续”谱成分更加突出，轴心轨迹非常紊乱，系统表现出“混沌”特征。

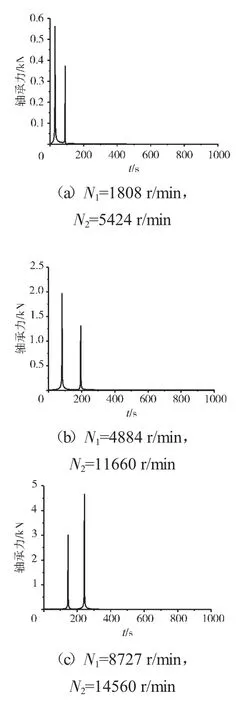
图20 支承不同心Case1情况下的支承4轴承力频谱

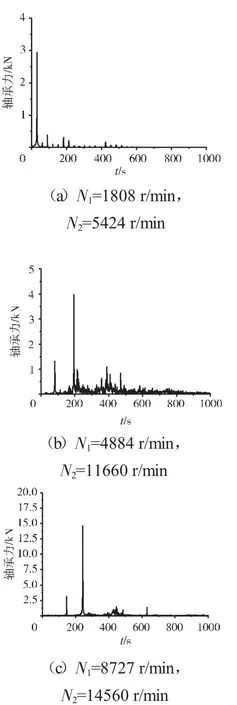
图21 支承不同心Case2情况下的支承4轴承力频谱

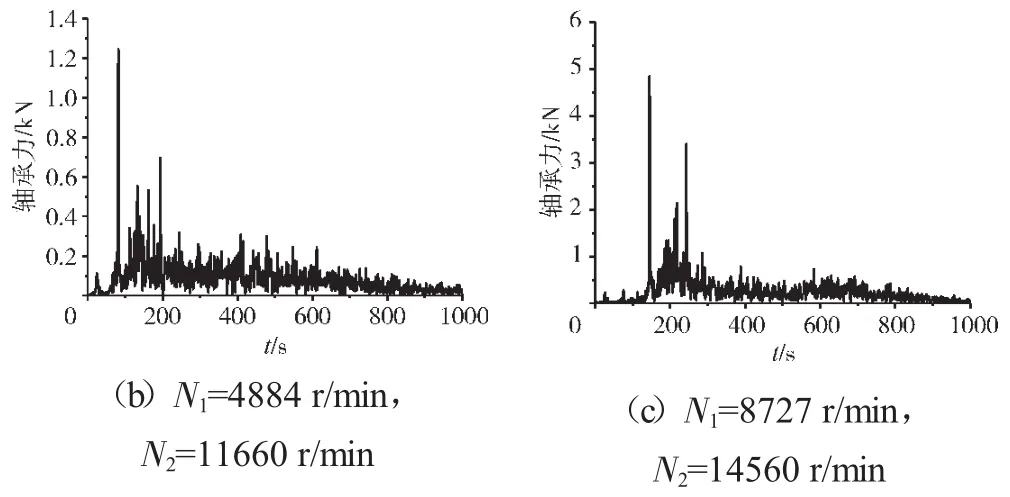
图22 支承不同心Case3情况下的支承4轴承力频谱

4 结论

将支承不同心模型与整机振动模型相结合，进行了不同心下的故障仿真计算，并比较了不同的支承不同心度下的支承轴承力、支承处转子节点加速度、机匣测点处的机匣节点力和机匣测点响应加速度。不同心度需要支承轴承的间隙补偿，不同心度越大，要求轴承间隙越大，过大的轴承间隙将引发轴承冲击，产生很大的轴承力，使转子运动出现混沌现象，从而影响转子运动的稳定性。同时，过大的轴承力将引发滚动轴承的疲劳破坏，对于中介轴承尤其如此，这也是实际航空发动机中介轴承容易损坏的重要原因之一。然而，机匣测点响应对不同心的灵敏度并不高，给实际航空发动机支承不同心的诊断带来困难。