基于在线滚动序列核极限学习机的涡轴发动机非线性模型预测控制
2018-09-17潘慕绚黄金泉
王 宁,潘慕绚,黄金泉
(南京航空航天大学能源与动力学院,南京210016)
0 引言
直升机是1个多自由度、强耦合的系统,与发动机系统之间相互耦合[1]。随着新一代直升机性能不断提高,对直升机控制系统、操纵品质和机动性的要求越来越高,各子系统复杂程度和耦合效应大大增加,传统串级PID控制方法难以获得较好的控制效果[2]。此外,直升机机动飞行时,由于旋翼扭矩相对于操纵量变化的滞后特性和发动机控制系统动态特性造成的不容忽视的时滞特性,使得发动机不能及时针对操纵量变化进行调整,因此,在设计发动机控制律时必须考虑这种滞后性,而传统串级PID方案处理上述时滞效应时显得能力不足,最终导致控制系统性能较差[3]。
模型预测控制(MPC)技术[4]由于具有对模型宽容性、有限时域滚动优化有效性以及在设计中考虑各种软硬约束可能性等突出特点,若将该动态优化技术应用到发动机控制系统中,对解决上述时滞效应问题、改善闭环系统动态特性无疑是1种可期待的控制方法。预测控制方法的核心是基于1个预测模型在一定控制时域内进行滚动优化控制,其间考虑到相关约束并利用反馈校正机制准确控制目标。预测控制方法的突出优点是可利用大量有效信息进行优化控制,在有扰动或模型失配的情况下具有良好的鲁棒性。
2007年,美国NASA研究中心在1次重要会议上介绍了有关智能发动机NMPC的应用[5]。从国内、外文献来看,NMPC在航空发动机控制方面已有相关探索研究[6-7];文献[8]利用神经网络训练预测模型实现了带旋翼负载的涡轴发动机在小扰动情况下的预测控制;文献[9-10]通过串联稳态非线性模型和ARX动态线性模型作为预测模型进行涡轴发动机动力涡轮转速控制;文献[11]建立MRR-LSSVR预测模型进行涡轴发动机预测控制;文献[12]通过在线滚动更新OPS-LSSVR预测模型进行涡轴发动机预测控制等。以上研究大多利用神经网络或者支持向量机进行多输出预测模型辨识,但神经网络以及支持向量机有自身的缺陷,如需要多次迭代,训练时间长,容易陷入局部最优解等。极限学习机(ELM)算法具有训练速度快、泛化能力强的特点,在辨识多输出参数耦合模型方面具有较大优势[13]。其中核极限学习机(KELM)由于具有可调参数少、收敛速度快、泛化能力强等诸多优点,在模型辨识等方面已经得到广泛的研究与应用[14-15]。此外,大多研究仅考虑了燃油量及燃油变化量限制约束,对于涡轴发动机控制问题,除了考虑以上约束限制外,还需要考虑发动机转速、燃气涡轮出口温度、压气机喘振裕度限制,保证发动机平稳、安全、可靠地工作。
本文针对涡轴发动机控制系统中时滞特性问题,提出了1种基于在线滚动序列的核极限学习机(OSS-KELM)的非线性模型预测控制方法。
1 NMPC控制结构
涡轴发动机控制的目的是保证当直升机操纵量发生改变时,发动机动力涡轮转速恒定,抑制动力涡轮转速的超调/下垂量。NMPC控制是1种基于有限时域带约束的目标函数的开环优化方法,运用非线性模型预测涡轴发动机未来时刻的输出,并利用在线滚动优化算法求解发动机动力涡轮转速控制器。本文提出的涡轴发动机NMPC控制方案原理如图1所示。
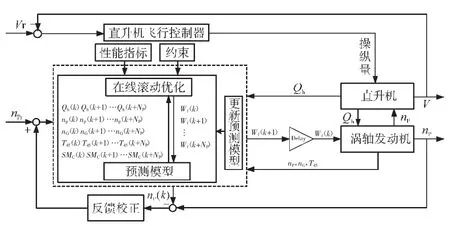
图1 涡轴发动机NMPC控制系统方案
NMPC控制器包括在线更新预测模型、在线滚动优化以及反馈校正3部分,其中预测模型能够实现在线更新,保证预测精度。预测模型根据当前时刻燃油Wf以及历史的输入和输出信息,在线实时预测发动机系统输出,如旋翼扭矩Qh、动力涡轮转速np、燃气涡轮转速nG、涡轮级间温度T45和压气机喘振裕度等;基于预测模型以有限时域带约束的动力涡轮转速恒定为寻优目标,利用SQP算法求解未来有限时域内的燃油输入,并将下一时刻的输入通过执行机构输入到发动机燃烧室;根据KELM模型与实际系统输出误差修正控制指令,提高控制精度。
2 预测控制器设计
2.1 OSS-KELM算法
当训练数据集过大时,学习算法中矩阵求逆计算耗时严重。而且对于复杂的直升机/发动机系统,系统参数变化速度较快,变化范围较广,离线辨识的预测模型精度难以保证。因此,若能根据系统实时有效信息在线辨识预测模型实现预测控制,可以改善控制系统控制品质。
文献[16]将离线KELM推广到在线训练,提出了在线序列KELM算法。但是该方法的缺陷是随着时间的推移,模型结构随训练样本的增加呈线性增长。为此,本文采用基于线性相关分析的滚动窗法进一步稀疏模型结构,称之为在线滚动序列核极限学习机(OSS-KELM)。
给定样本集{(xi,yi),i=1,2,…,N},其中,xi=[xi1xi2…xin]T∈n,yi=[yt1yt2…yim]∈m,N 为样本数。针对具有 L 个隐含层神经元的ELM网络,这个学习问题可以描述为
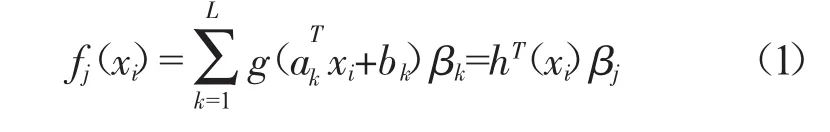
式中:ak=[a1ka2k… ank]T,为连接第k个隐含节点的输入权值向量;b为第k个隐含节点偏置;h(x)=[g(ki+b1)g(+b2)… g(+bL)]T,为特征映射;g(x)i为隐含层神经元激活函数;βj=[β1β2… βL]T,为第 j个输出参数输出权值向量。
在ELM中,学习问题可以理解为寻找预测函数f保证 (fx)i→yi,建立如下最优化问题
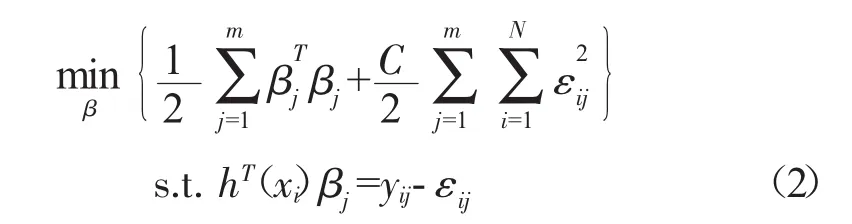
式中:C为人为选定的正则化参数;εij为松弛变量,表征ELM预测值与实际值之间的误差。
求解式(2)得到

式中:H=[h(x1)h(x2)… h(xN)]T,为隐含层输出矩阵;Y=,为样本输出向量;IN为1个N维的单位矩阵。
借鉴 SVM等核方法,定义核函数 k(x,y)=〈h(x)h(y)〉,〈·,·〉表示特征映射的内积,定义核矩阵 K 为
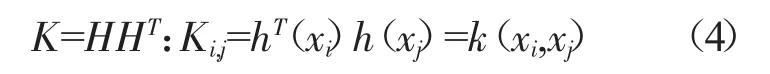
将核函数代入式(1)、(3)得到 KELM的预测函数
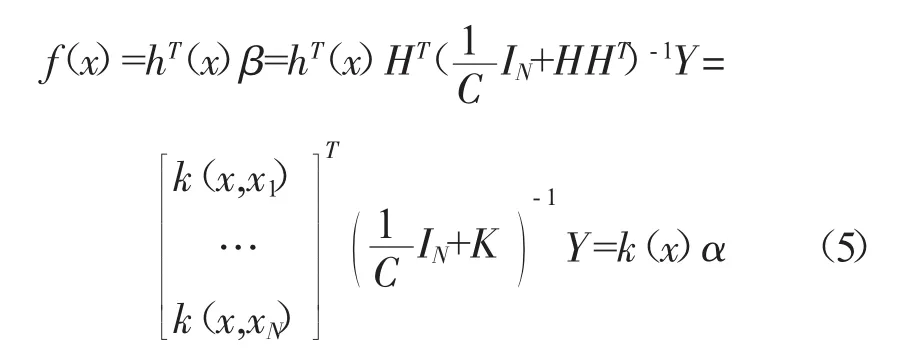
式中:x为待估计样本输入向量;α为KELM的输出权值
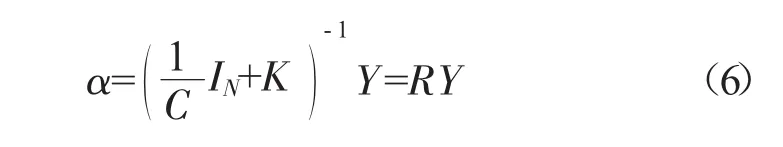
由于OSS-KELM训练可以看作是1个迭代学习过程,每次新样本加入都需要更新输出权值α以及求解逆矩阵R,计算耗时费力,为解决这一问题,考虑核矩阵迭代求逆加快计算速度。
定义1个在线索引集合Q,利用第1个样本初始化逆矩阵R1和输出权值向量α1,此时Q={1}。假设在第n+1步时,在线索引集合Q={Qi|i=1,2,…,q},q为在线索引集合Q元素的个数,训练样本数据集为(X,Y),其中,X=[xQ1xQ2…xQ4]T,Y=[yQ1yQ2…yQ4]T。
新加入样本数据(xn+1,yn+1),则有
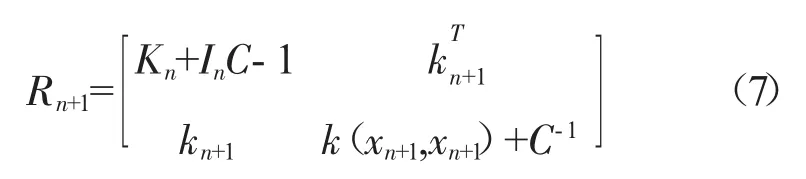
式中:Kn为第 n 步计算得到的核矩阵,kn+1=[k(xQ1,xn+1)k(xQ2,xn+1)… k(xQ4,xn+1)]T。
Sherman-Morrison公式[17]:给定矩阵A以及D、V、U,以下等式是成立的。
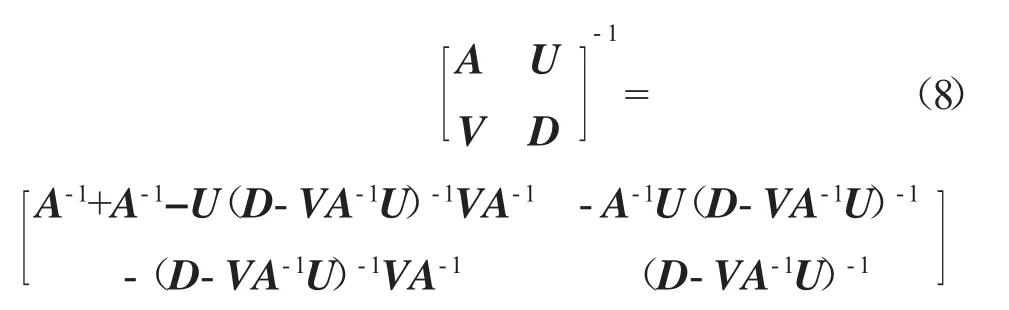
由于 Rn=(K+InC-1)-1在第n步中已经得到,则求逆问题的更新式为
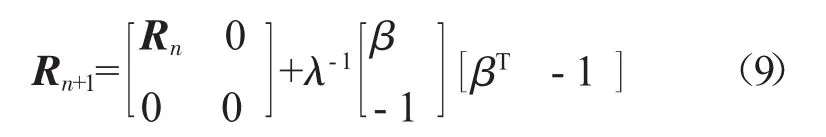
式中:β=Rnkn+1;λ=(k(xn+1,xn+1)-β),将得到的求逆结果代入式(6),得到第n+1步的输出权值

这样逆矩阵以及输出权值便可以通过迭代计算得到。考虑到输出权值向量的维度随训练样本的增加呈线性增长,为了降低输出权值向量维度,引入线性相关性作为评判的准则,从而降低数据的冗余程度,精简模型的结构。由于在线数据是按时间序列交替出现的,在第n+1步根据式(12)判断新加入的样本(xn+1,yn+1)与当前样本训练样本集合(X,Y)的线性相关程度
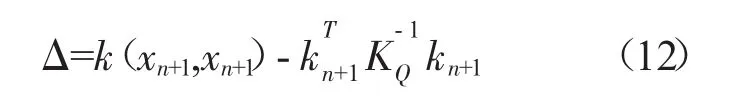
式中:KQ=(kij)∈q·q,kij=k(xi,xj),i,j∈Q。
该算法中尽管样本数没有上限,对于实时性要求很高的在线预测模型而言,仍不能满足精简模型的要求。下面以滚动窗法进行改进(如图 2所示),当n+1时刻加入新样本(xn+1,yn+1)时,首先判断新样本与当前样本集(X,Y)的线性相关程度,定义1个较小的常数 δ,如果 Δ<δ,不引入新样本对在线索引集合Q以及模型进行更新,否则,引入新样本更新(X,Y),Q以及α,若此时样本窗口中的数据量超过窗口规模L+1,则剔除离当前时刻最远的样本数据(xQ1,yQ1),将扩维后的逆矩阵R进行降维,得到降维后的逆矩阵R。根据Sherman-Morrison定理[18]分解逆矩阵

式中:R11∈、R12∈1×(L+1)、R21∈(L+1)×1,以及 R22∈(L+1)×(L+1),为 R 的分块矩阵;为剔除(xQ1,yQ1)后的核矩阵;g=k(xQ1,yQ1)+C-1,G=[k(xQ1,yQ2)k(xQ1,yQ3)… k(xQ1,yQn+1)]
根据式(13)可以得到,剔除(xQ1,yQ1)后的逆矩阵
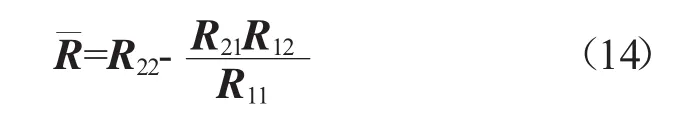
剔除(xQ1,yQ1),构造新的样本集合(X,Y)以及在线索引集合Q,此时输出权值矩阵

从而保证输出权值α维度不变,即滚动窗口数据规模恒定,从而提高计算实时性。
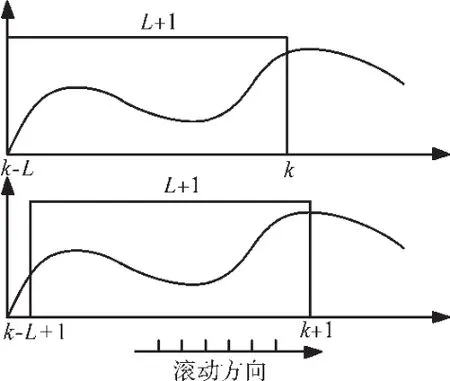
图2 滚动窗原理
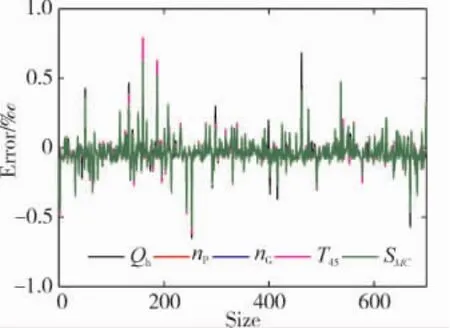
图3 H=3 km、VX=20 m/s模型相对误差
本文在高度H=1 km、前飞速度VX=0 m/s状态下,对直升机以及发动机输入进行充分激励,取其归一化后动态响应数据,利用上述的多输出OSS-KELM算法进行模型训练,在包线范围内对模型泛化能力进行验证。限于篇幅,仅列出高度H=3 km、前飞速度VX=20 m/s的测试相对误差(如图3所示),模型精度可达1‰,满足设计要求,其他点精度与之类似。
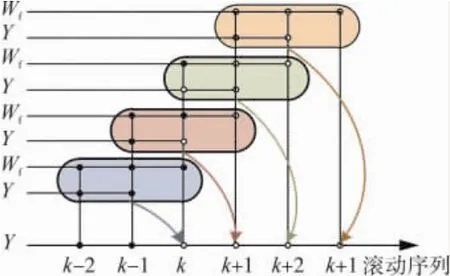
图4 迭代预测模型
2.2 基于在线滚动KELM的NMPC设计
利用2.1节设计的OSS-KELM算法辨识涡轴发动机KELM动态模型,模型输入为当前时刻燃油Wf、历史时刻的Wf、旋翼扭矩Qh、燃气涡轮转速nG、动力涡轮转速np、涡轮级间温度T45以及压气机喘振裕度SMC,输出为当前时刻的 Qh、nG、np、T45和 SMC。在线辨识KELM时,首先将前一时刻系统输出、输入以及历史信息看作新样本,并与之前训练样本进行相关性分析,若新样本与当前样本线性不相关,则更新输出权值矩阵α,同时若当前样本数量达到窗口规模L+1,则对扩维的逆矩阵R进行降维处理,保证数据窗口规模恒定不变以提高计算实时性。此时,KELM动态模型可以描述为
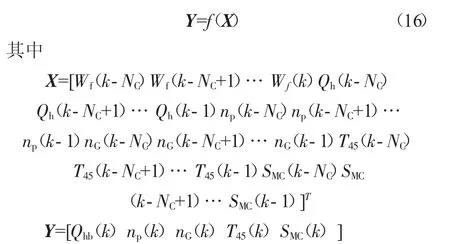
为了减少计算量,需要降低模型结构的复杂程度,而同时又要保证预测模型的预测精度,因此需要选择合适的预测模型结构。由于发动机一般可以简化为1个2阶过程,因此可以选择控制时域NC=2。由于控制器通过滚动优化求解动力涡轮转速恒定为目标函数的优化问题,使得下一时刻的输入总是最优值,则预测时域Np=3,可以按照如图4所示的方案,由当前时刻燃油Wf(k)、未来Np步的燃油 序 列 {Wf(k+1),Wf(k+2),…,Wf(k+Np)}、历史输入和输出信息根据式(16)推导出迭代NP步之后的预测模型


基于上述的OSS-KELM学习算法辨识的预测模型,利用SQP规划算法实现在线滚动优化求解约束下的最优问题,即给定燃油量、涡轮转速、涡轮级间温度以及喘振裕度限制,保证转速恒定为优化目标,进行控制器求解。本文选择如下的二次型性能指标
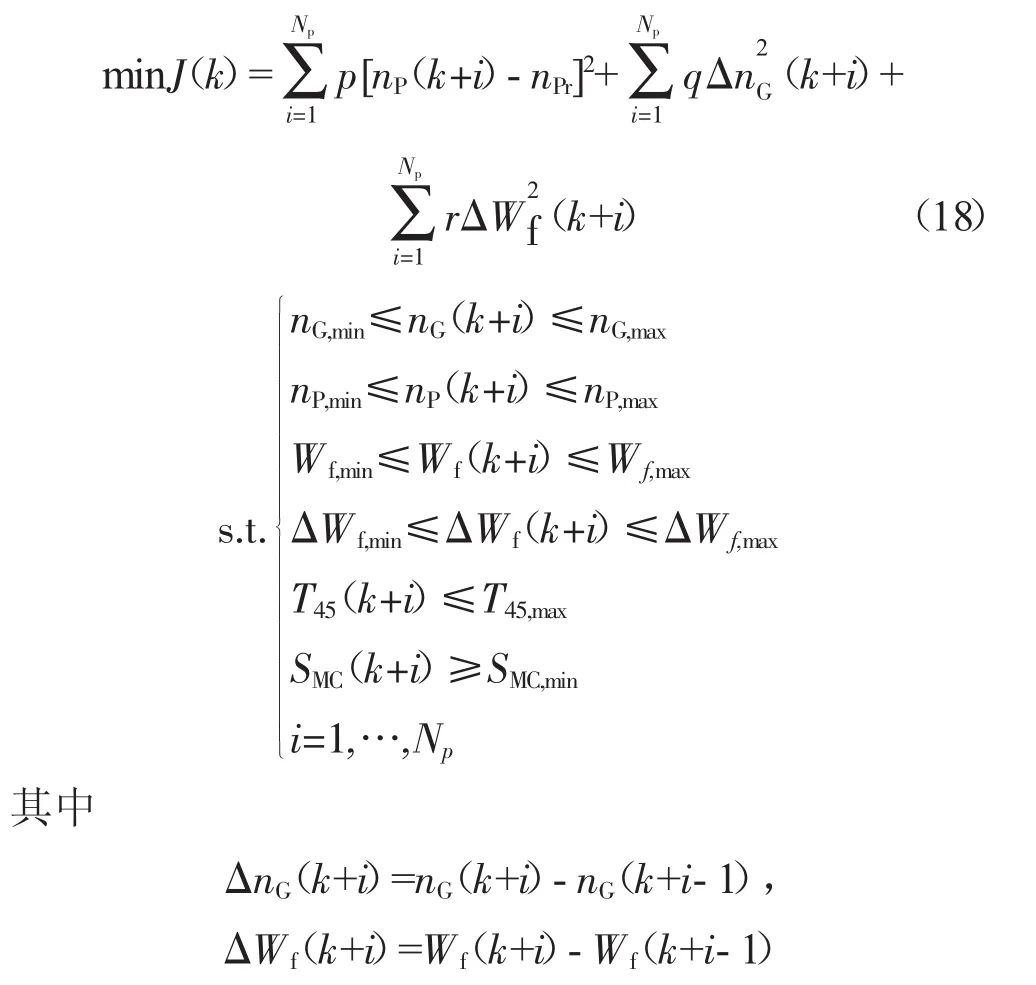
式中:p、q、r为各目标权值。
该二次型指标函数可以保证动力涡轮转速恒定的同时,尽量减少燃油消耗和降低转速波动。通过滚动优化求解约束下的最优问题,即可计算出使得二次型性能指标最小的燃油流量序列{Wf(k+1),Wf(k+2),…,Wf(k+NP)},而后将Wf(k+1)与当前时刻实际燃油流量Wf(k)的差值作为燃油补偿输入。除此之外,引入补偿燃油限制,克服因模型失配造成的不稳现象,从而在满足发动机对操纵量变化快速响应需求的同时抑制系统的波动。
由于NMPC是通过模型预测系统未来输出进行控制的,模型输出与实际发动机输出之间的误差就必然存在。为了保证控制精度,本文通过上一时刻发动机输出与预测模型输出的误差对控制指令进行修正,从而减小控制误差。
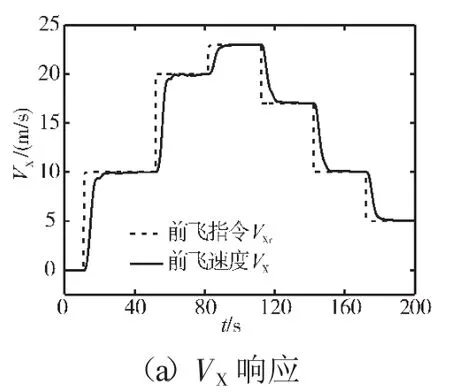

图5 H=3 km、VX=20 m/s前飞加减速控制效果
3 仿真验证与分析
基于某型直升机/涡轴发动机综合仿真平台,在主频3.30 GHz/内存4 GB的仿真环境下,分别对直升机前飞和垂飞加减速机动飞行进行仿真,仿真步长为20 ms,数据作归一化处理,验证本文提出的基于OSS-KELM的NMPC控制方案,并与传统串级PID控制进行对比分析。经数值仿真验证在每个20 ms的仿真周期内,NMPC控制器计算花费时间小于5 ms,满足实时性要求。
直升机在高度H=1 km,前飞速度VX=0 m/s的状态下平飞加减速的响应如图5所示。
从图5(b)可见,NMPC动态控制效果显著优于串级PID控制,NMPC控制器对应的动力涡轮转速最大超调量为0.56%,而串级控制器为2.21%,NMPC控制器对应的最大下垂量为0.68%,而串级控制为2.65%,这是由于在直升机机动飞行过程中,NMPC相对于串级控制,采用预测手段,有效地根据历史信息预测系统未来输出,预测旋翼需用扭矩以及发动机转速等参数的变化,通过求解带约束的以减小动力涡轮转速波动以及降低燃油消耗的性能指标,保证每一时刻的燃油输入为最优值,所以NMPC控制对应燃油波动量小于串级控制,而且可以快速地调节燃气涡轮转速和降低动力涡轮转速波动量,使得动力涡轮转速下垂/超调量很小。

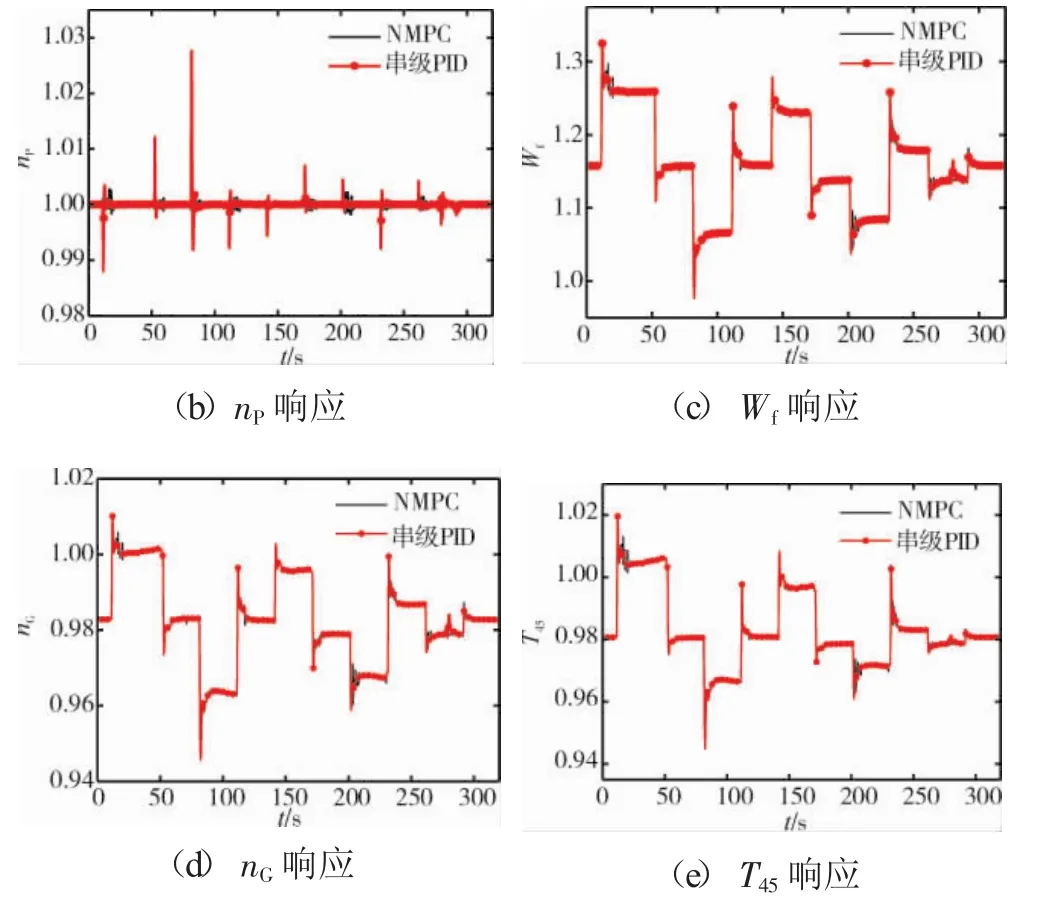
图6 H=3 km、VX=20 m/s垂飞加减速控制效果
为进一步验证NMPC的控制效果,针对直升机垂飞加减速过程进行仿真验证。直升机在高度H=1 km、垂飞速度VZ=0 m/s状态下垂飞加减速机动飞行的仿真结果如图6所示。
从图6(b)可见,NMPC控制器的动态效果明显优于串级控制,NMPC控制器对应的动力涡轮转速最大超调量为0.27%,而串级控制器为1.98%,NMPC控制器对应的最大下垂量为0.16%,而串级控制器为1.53%,说明了采用NMPC方案能够通过预测旋翼扭矩、涡轮转速等未来时刻输出数据,在线滚动优化求解输出最优的输入,使得发动机快速满足旋翼功率的需求,动力涡轮转速能够快速响应并调节至稳定,从而有效地抑制动力涡轮转速超调/下垂,提升控制系统控制品质。
4 结束语
本文针对涡轴发动机控制系统设计,基于直升机/发动机综合仿真模型,提出了1种非线性模型预测控制方法。采用多输出在线滚动序列核极限学习机训练预测模型,利用在线滚动优化手段和反馈校正机制实现带约束的模型预测控制。最终运用于直升机机动飞行过程中,仿真结果表明,与传统串级控制相比,NMPC控制器能够有效地抑制动力涡轮转速超调/下垂量,具有更好的控制性能。
