车轮多边形对车辆动力学的影响分析及在线诊断方法研究*
2018-09-12戚潇月宋冬利张卫华
戚潇月, 宋冬利, 张卫华
(西南交通大学 牵引动力国家重点实验室, 成都 610031)
车轮多边形化普遍存在于高速列车车轮中,它是车轮不圆顺的一种形式,即车轮半径沿圆周方向呈现出一种周期性不圆顺,它会引起车辆轨道系统一系列动力响应的变化,对行车稳定性和安全性以及车辆轨道系统各个部件使用寿命产生严重影响,还会产生较大冲击和滚动噪声[1-2]。1998年德国ICE型高速列车行车脱轨事故是由于弹性车轮发生多边形化问题,轮箍在车轮不圆激励作用下引起疲劳断裂,导致列车脱轨而产生。除此之外车轮多边形化还会造成齿轮箱开裂和螺栓松脱等故障。
研究结果证明,考虑轮对弹性后车辆的动力学计算比刚性轮对更加准确,而将车辆轮对考虑为弹性后,它会与整个车辆系统的振动耦合,从而导致轮轨动态载荷发生变化[3-4]。车轮多边形化主要产生于轮轨接触,因此很必要在研究车轮多边形化问题中考虑轮对为弹性体以得到更准确的车轮多边形化引起的车辆系统的动态响应特征。
高速列车车轮多边形化问题不仅影响列车的高速、平稳运行,而且会导致轮轨系统产生强烈的冲击振动,危及行车安全,因此有必要开展对车轮多边形的在线监测和诊断。国内部分学者做了相关的工作:宋颖[2]提出了基于PVDF压电传感技术的铁路轮轨力实时监测方法,结合各种车轮不圆激励作用下的轮轨动力作用特征,在轨道上采用PVDF压电薄膜作为传感原件通过测量钢轨应变实现轮轨接触力的实时监测,但此方法的监测方式更利于科研研究较难运用于工程实际。李亦璠[5]提出一种基于轴箱加速度改进的EMD的Hilbert谱方法,有效地对车轮失圆问题进行了定性的识别和定量的判断,不过在较为准确的实现故障的定量判断方面存在一定不足。
基于对国内某型动车组的长期跟踪监测后积累的大量轴箱加速度数据,发现车轮多边形化会引起轴箱振动数据的明显变化。通过仿真计算结果,结合大量的现场多边形入库检测,提出一种基于轴箱垂向加速度的多边形在线诊断方法,可以在线辨别多边形阶数和深度,总体研究思路如下:
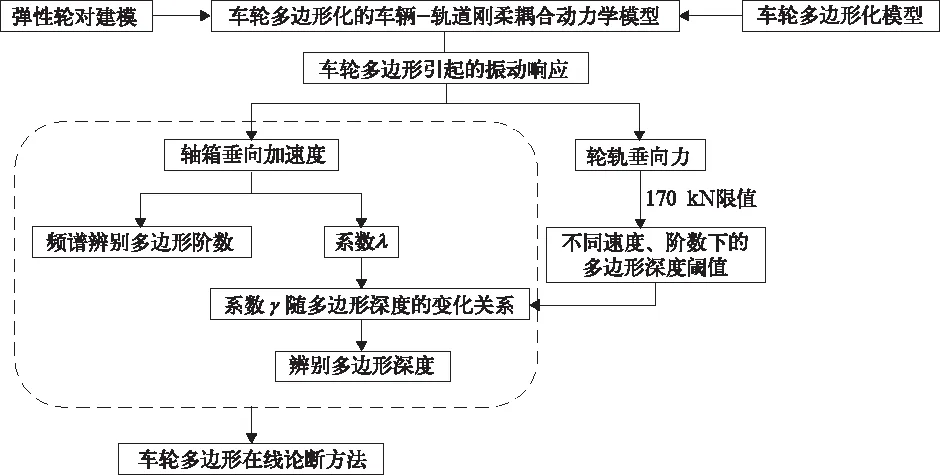
图1 建模流程
1 车轮多边形化的车辆轨道刚柔耦合动力学建模
1.1 基于ANSYS与SIMPACK联合仿真的车辆轨道刚柔耦合建模
采用FEMBS[6]来生成弹性轮对,FEMBS是有限元分析软件和SIMPACK之间的接口,在此有限元软件为ANSYS。思路如图2。
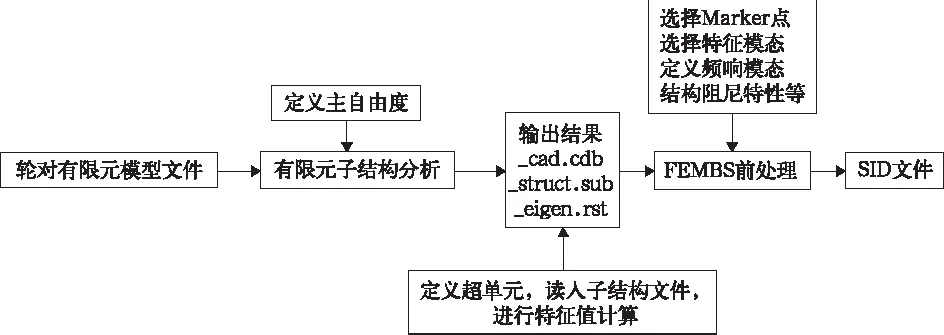
图2 SIMPACK和ANSYS联合仿真建模流程图
首先在SOLIDWORKS中参照国内某型动车组轮对建立了三维实体模型,经简化处理后导入有限元软件ANSYS。采用八节点六面体实体单元对其进行网格划分,然后对轮对有限元模型进行子结构分析[7],在此共选出79个主节点,共237个主自由度。对生成的子结构进行自由模态分析,因没有对轮对施加约束,所以前6阶是刚体振动模态频率为零。轮对第7阶振型为车轴扭转,8、9阶是车轴的1次弯曲,10、11阶为车轴2次弯曲,第12阶为车轮辐板轴向对称变形[8]。轮对有限元模型、主自由度集和轮对子结构分别如图3~图5。

图3 轮对有限元模型

图4 轮对主自由度集
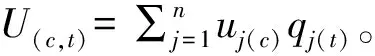

图5 轮对子结构
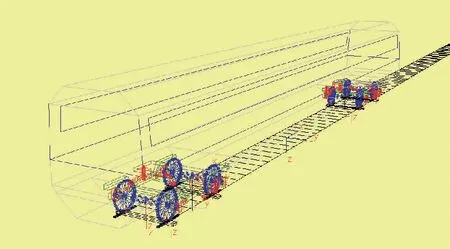
图6 基于轮对弹性的刚柔耦合动力学模型
此车辆模型以300 km/h的速度在直线上运行,观察轮轨垂向力和轴箱垂向加速度的时频如图7。可以看出,考虑轮对的弹性后轮轨垂向力明显大于刚性轮对,弹性轮对轴箱垂向加速度也较刚性轮对大,但二者差异并不明显。弹性轮对的轮轨垂向力和轴箱垂向加速度均出现了28.74 Hz左右的主频,原因是考虑了轮对弹性后,当轮对受到轮轨垂向力作用时,会产生弯曲变形,此频率为高速运行时轮对的弯曲振动与构架垂向运动的耦合频率。此耦合振动会加强轮对的垂向振动,继而增大轮轨垂向力,可见考虑轮对的弹性可以更加真实的反映车轮轮轨力的变化规律。车轮多边形化会引起轮轨力的剧烈变化,因此在计算多边形化车轮对车辆轮轨力影响时,考虑轮对的弹性可以使得计算结果更加真实。
1.2 车轮多边形化模型
采用一种简谐波函数的方法来定义车轮多边形[10],在车轮滚动一周内,将车轮圆周不平顺的轮径差考虑成谐波函数:
其中,n为车轮多边形谐波阶数,A为多边形深度,β0为相位角。
此方法是通过修改车轮外形来模拟车轮多边形。实际中每个车轮上不只产生一阶多边形,通常存在几种不同阶数的多边形叠加,我们只考虑占主导地位的某阶多边形。
综上可得到车轮多边形化的车辆轨道刚柔耦合动力学模型,此模型不仅可以模拟不同阶数的车轮多边形,还能改变多边形的深度和相位差,在考虑轮对弹性变形的基础上更加真实的反应车轮多边形化引起的车辆振动响应。
2 车轮多边形对车辆动力学的影响
2.1 车轮多边形对轮轨垂向力和轴箱垂向加速度的影响
在车辆系统动力学模型中通过修改车轮外形模拟不同阶数、深度的车轮多边形,已知车轮多边形化主要影响车辆系统的垂向振动[10],通过提取轮轨垂向力和轴箱垂向加速度两个动力学指标来研究不同速度下,不同阶数和深度的车轮多边形对车辆动力学性能的影响。
由大量的多边形入库检测数据可知此动车组车轮高阶多边形主要为17~21阶,以220~300 km/h为例计算车辆在不同运行速度,不同多边形阶数和深度时对应的轴箱垂向加速度和轮轨垂向力,其变化规律如图8。

图8 轮轨垂向力和轴箱垂向加速度有效值随速度、阶数和深度的变化规律
可见轮轨垂向力有效值随着车辆运行速度、多边形阶数和深度的增大而增大。轴箱加速度有效值在260 ~300 km/h时随着速度、阶数和深度的增大而增大,当速度稍小时变化呈现一定的波动性。可以看出列车在高速运行时,车轮高阶多边形会在轮轨接触表面产生剧烈冲击并且加剧车辆部件振动,随着速度和多边形深度的增加这种影响愈加明显。
2.2 轴箱垂向加速度实测数据分析验证
选取此车辆3段不同旋后里程下相同速度相同运行区间相同时刻的轴箱垂向加速度,并对其做FFT变换观察,如图9。

图9 实测轴箱垂向加速度时域和频谱图

3 车轮多边形在线诊断与阈值研究
车轮多边形的存在加剧了轮轨之间的接触作用和车辆部件振动,同时还会激发一些特定的振动模态。这不仅使得车辆系统振动加剧而且在一定程度上影响了行车安全。由于动车组在运行过程中无法对车轮多边形状况进行实时测定,所以文中提出一种在线诊断车轮多边形阶数和深度的方法,并且给出了对应的多边形深度阈值。
3.1 多边形阶数在线诊断方法

图10 轴箱垂向加速度频谱图
可以看出,轴箱垂向加速度频谱图分别出现了489,517,547,576,605 Hz的主频,分别对应车轮名义滚动圆半径为0.46 m车辆运行速度为300 km/h时17~21阶多边形的特征频率。
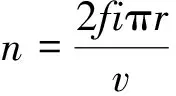
3.2 多边形深度阈值研究
图11为不同速度下17~21阶多边形轮轨垂向力最大值随速度和多边形深度的变化趋势。
当多边形阶数一定时,轮轨垂向力最大值随车辆运行速度和深度的增大而增大,车轮出现21阶多边形时的轮轨垂向力最大值可达180 kN,是正常车轮轮轨垂向力的2倍左右,可见列车在高速行驶的情况下车轮多边形化会显著影响轮轨垂向力。
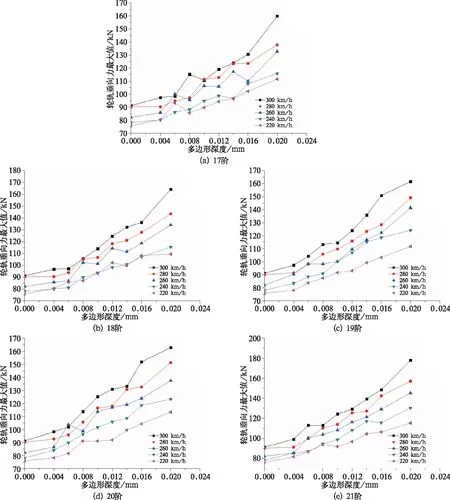
图11 轮轨垂向力最大值随多边形阶数、深度的变化规律
中国《高速试验列车动力学强度及动力学规范》中规定高速列车车轮作用于轨道上的轮轨垂向力极值P不应该超过170 kN,所以为保证行车安全,需要限制多边形的深度。针对高速列车车轮多边形化的动态特性,提出由轮轨垂向力限值标准来判定17~21阶多边形车轮的深度阈值,得到不同速度下的深度阈值如表1。可见多边形阶数一定时,多边形深度阈值随着速度的增加而减小,在一定程度上验证了随着速度的增大轮轨垂向力也随之增大的规律。
3.3 多边形深度在线辨识方法研究
车辆在实际运行过程中轮轨垂向力是不容易获得的,而对车辆的跟踪监测中容易获取轴箱加速度信息,为了防止车轮多边形深度超限引起轮轨垂向力增大影响车辆性能,可以根据轮轨垂向力、多边形深度与轴箱垂向加速度之间的联系,建立基于轴箱垂向加速度的多边形深度在线辨识方法。
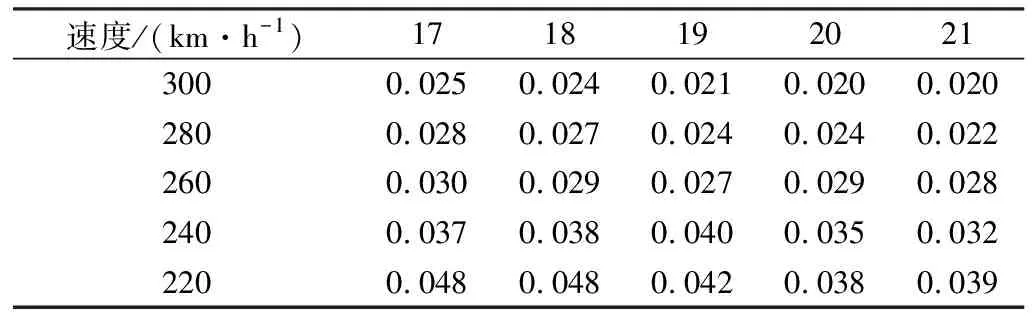
表1 不同速度条件下17~21阶多边形对应的深度阈值
提出如下定义的一个系数:
即对轴箱垂向加速度做FFT变换,计算多边形特征频率段的幅值占除去此频率段后整个频段幅值的比例。其中fi为多边形特征频率,Δf为频率分辨率,Af1为频率f1对应的幅值,Af2为频率f2对应的幅值。
仿真采样频率为2 000 Hz,因此FFT变换后只能得到0~1 000 Hz的频谱分析图,而实际跟踪测试动车组加速度传感器采样频率为102.4 kHz,其频率分辨率为12.5 Hz,因此在此设定多边形的特征频段为(fi-12.5,fi+12.5),可计算出不同速度下17~21阶多边形对应的系数λ。在此以速度为300 km/h时为例,车轮出现17~21阶多边形时轴箱加速度系数λ随着深度的变化规律如图12。
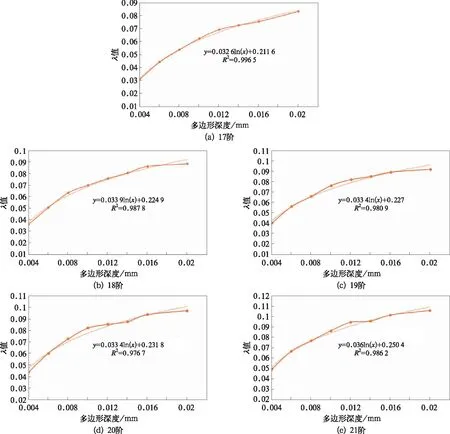
图12 λ随多边形深度的变化规律
可见速度和多边形阶数一定时,λ随着多边形深度的变化规律可以用指数函数表示,因此得到轴箱垂向加速度后计算得到系数λ,根据λ与深度之间的关系可求得对应阶数下多边形的深度,从而辨别深度是否超限。同理可得其他速度等级下λ随阶数和深度变化的类似规律,在此不叙述。
3.4 实测数据验证
在实际动车组多边形入库检测时当车轮表面粗糙度水平达到20 dB时即建议车轮旋修,且粗糙度等级为20 dB时对应的多边形深度为0.01 mm,选取此动车组车辆某一段轴箱加速度数据,滤波后对其做FFT变换如图13。
可见其频谱出现了600 Hz左右的主频,如前所述根据轴箱加速度频谱图辨别多边形阶数,结合轮径信息和速度信息得到多边形阶数为21阶。计算得到系数λ为0.097,根据300 km/h时21阶多边形系数λ随多边形深度的变化关系可求得对应的多边形深度为0.014 mm,对应的粗糙度等级约为23 dB,与多边形检测结果相近。
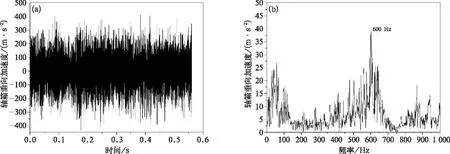
图13 实测轴箱加速度
4 结 论
采用谐波函数的方法模拟车轮多边形,建立了车轮多边形化的车辆轨道刚柔耦合动力学模型,验证了车轮的弹性变形会影响轮轨接触作用和车辆部件振动。通过仿真分析了车轮17~21阶高阶多边形对车辆动力学性能的影响,在此基础上提出了车轮多边形在线诊断方法,结论如下:
(1)轮轨垂向力和轴箱垂向加速度随着多边形阶数和深度的增加而增加,可见车轮多边形化会显著影响车辆系统的垂向振动,加剧了轮轨动态接触并增强轴箱振动。
(2)根据轮轨垂向力限值170 kN标准得到不同速度、不同阶数下的多边形深度阈值,发现随着速度和阶数的增加深度阈值大致呈降低趋势。
(3)建立了车轮多边形的在线诊断方法,提出轴箱垂向加速度特征频辨别多边形阶数,定义了轴箱垂向加速度系数λ,揭示了λ与多边形深度之间的函数关系,进而建立了多边形深度在线辨别方法。
