基于稳定性分析的动力集中动力车车轮踏面匹配研究

2018-09-12闫兆盈陈国胜邓小星

铁道机车车辆 2018年4期

闫兆盈，罗贇，陈国胜，邓小星

(1 西南交通大学牵引动力国家重点实验室，成都 610031；2 大功率交流传动电力机车国家重点实验室，湖南株洲 412001)

轮轨匹配关系是影响车辆动力学性能和轮轨磨耗的重要因素，选择合适的轮轨匹配型面对提高车辆运行稳定性有重要意义。自从20世纪30年代Heumann提出磨耗型车轮踏面以来，我国的铁路研究人员对磨耗型踏面做了大量的研究。[1]2003年3月中华人民共和国铁道部发布了机车车辆车轮轮缘踏面外形标准，该标准取消了锥型轮缘踏面，规定了车辆车轮用踏面形状LM，LMA和机车车轮用踏面形状JM，JM2和JM3。[2]

黄运华等分析比较了我国LM踏面和德国DIN 5573踏面对地铁车辆动力学性能的影响，结果表明采用DIN 5573踏面时车辆的运行稳定性优于LM踏面。[3]张剑等基于轮轨接触几何、非赫兹滚动接触、车辆轨道耦合动力学计算分析了地车车辆常用的LM型踏面、S1002型车轮踏面分别与60 kg/m钢轨匹配特性，综合分析表明LM型踏面与60 kg/m钢轨的接触状态较好。[4]刘高坤等基于某直线电机地铁车辆分析了LM/CHN60与LMA/CHN60两种匹配的轮轨接触几何及动力学性能，结果表明该地铁车辆采用LMA踏面能获得更好的综合动力学性能。[5]孙善超等基于先锋号客车基本参数建立的车辆动力学模型，分析轮轨几何参数对高速车辆运行平稳性和稳定性的影响，研究表明：增大轮对内侧距(增大等效锥度)可以改善舒适性，减小磨耗，提高临界速度。[6]

国外学者对轮轨踏面匹配做了大量的研究，Novales和Polach等优化轮轨型面匹配参数，通过动力学仿真可知车辆动力学性能有所提高。[7]REN Z等分析比较了日本、欧洲的轮轨几何关系差异，为高速轮轨关系的深入研究提供了基础。[8]Shevtsov对北美货运车辆的车轮和钢轨滚动接触进行模拟和试验，测试其滚动接触疲劳性能，进一步分析车辆运行性能。[9]

以160 km/h速度等级的动力集中动力车为研究对象，对比分析了JM3和LMA踏面与60 kg/m钢轨匹配的运动稳定性；并基于振动模态，结合一系纵向刚度分析踏面磨耗过程中动力车稳定性的变化情况。

1 动力车计算模型

采用SIMPACK多体动力学软件建立2B0轴式的动力车动力学模型，如图1所示，该模型包括一个车体、两个动力转向架。动力车物理模型、自由度及广义坐标参见文献[10]，车体和构架间由二系悬挂装置连接，二系悬挂装置由高圆弹簧(每侧两组)、两个抗蛇行减振器、两个横向减振器、两个垂向减振器构成；构架和轮对之间由一系悬挂装置连接，一系悬挂装置由一系弹簧、转臂式轴箱拉杆和垂向减振器组成，驱动装置采用弹性架悬方式。驱动装置具有六个自由度，驱动装置与构架悬挂座具有三向平动和转动刚度与阻尼，摆杆相对于构架可以有两个转动自由度，动力车模型自由度总数为122，建模中考虑了轨枕的弹性，动力车主要参数：轴重19.5 t，轴距2.9 m，转向架定距9.1 m，计算最高速度为210 km/h，构造速度为160 km/h。

2 新轮新轨线性稳定性计算

图1 整车动力学模型

图2 新轮新轨动力车根轨迹曲线

图2是JM3和LMA踏面分别与60 kg/m钢轨匹配时，进行Harmonic线性化[11]后动力车的根轨迹曲线，根轨迹曲线是指当系统中某个参量由零到无穷大变化时，其闭环特征根在平面上移动的轨迹，以横坐标表示模态的实部(自然阻尼)，纵坐标表示模态的虚部(振动频率Hz)，[12]变化的参数是速度从80～500 km/h，速度增量为10 km/h，故图中每一条根轨迹曲线都是由43个“+”号组成，且随着速度的增加，“+”号的形状也变大。图中还给出了速度160 km/h时，各主要刚体的振动频率。理论上，当系统的所有特征根实部全为负值时，系统的运动是稳定的。实际上，在机车车辆应用领域，阻尼很小时系统的平稳性将受到影响，考虑到安全裕量问题，当自然阻尼即横坐标超过-5%时，即判定出现蛇行运动失稳。

图2中每一条根轨迹都是动力车模型中一个振动模态随速度变化的轨迹。随着速度的提高，变化甚微的模态对应的频率是刚体的固有振动频率,其中有多个模态的阻尼随速度的提高而减小。

一系纵向刚度为15 MN/m，采用JM3踏面时，在最高速度下最危险模态的自然阻尼为负，而且阻尼比较大，动力车稳定性非常高，线性临界速度大于500 km/h；采用LMA踏面时，失稳模态是车体侧滚，临界速度为320 km/h。

LMA踏面与60 kg/m钢轨匹配时(轨底坡1/30),在轮对横移量y<6 mm时等效锥度约0.033。而JM3踏面的等效锥度约0.117。两种匹配关系在160 km/h运行速度下车体侧滚、转向架蛇行、轮对横向的频率及车体侧滚的阻尼差别较大，随着速度的增大同一振型模态的变化趋势也不同。

3 新轮新轨非线性稳定性计算

在计算动力车非线性稳定性时，截取一段长度为50 m的AAR5级不平顺时域谱作为激扰，动力车以一定速度通过不平顺后，在无不平顺直道上继续运行到300 m时，考察第一轮对横向振动位移的收敛和发散情况来判断其稳定性，结果见图4。计算结果表明，采用JM3动力车的蛇行失稳临界速度为340 km/h；采用LMA踏面为160 km/h，通过调整动力车参数(抗蛇行减振器卸荷阻力，卸荷速度及关节刚度)也不能达到临界速度快速提高的效果。

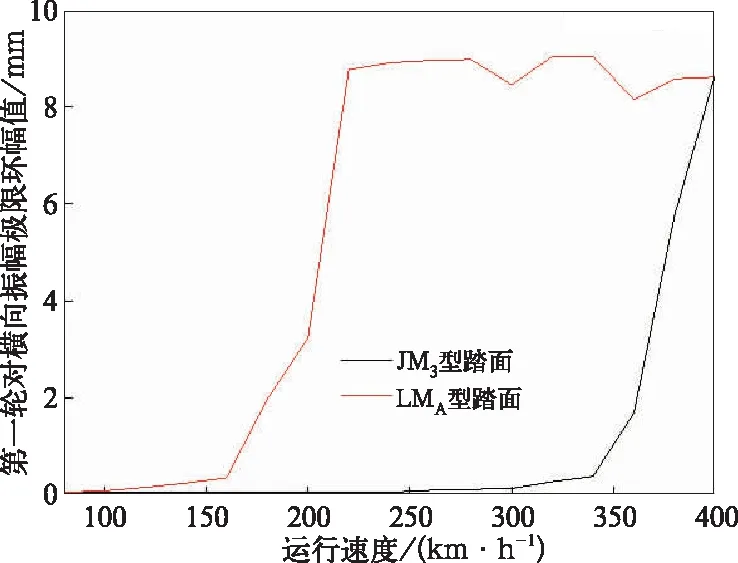
图3 非线性临界速度计算结果

4 等效锥度对整车线性稳定性的影响

4.1 临界速度计算

以下计算采用JM3踏面进行Equivalent线性化[11]。通过根轨迹法计算分析一系纵向刚度的大小在不同等效锥度下对动力车稳定性的影响。计算结果见表1，在整个服役过程中，随着等效锥度的变化，动力车也能保证160 km/h运行时的运动稳定性。

表1 等效锥度λ与一系纵向刚度kx对临界速度vcr(km/h)的影响

从计算结果来看，临界速度随着等效锥度的增大先增后减；在不同的一系纵向刚度下，出现临界速度最大值的等效锥度值随着刚度增大而增大。

在相同等效锥度下，临界速度随着一系纵向刚度增加而先增大，当一系纵向刚度超过某一分界后，临界速度逐渐减小，随着刚度增加对其影响程度变缓。当一系纵向刚度为5 ～10 MN/m时，大锥度下的临界速度较低，当一系纵向刚度大于35 MN/m时，在小锥度下临界速度较低。所以该动力车一系纵向刚度可取15～30 MN/m，在该范围内，当车轮踏面从JM3新轮开始，磨耗到限(等效锥度为0.5)过程中，不同等效锥度下动力车稳定性均好。由于没有车轮磨耗到限的踏面外形，无法计算相应的非线性临界速度，从锥度为0.033和0.117 的线性临界速度是非线性临界速度的两倍多关系，可以推断在车轮磨耗到限过程中，动力车非线性稳定性可以满足160 km/h的运行要求。

4.2 等效锥度变化引起整车失稳危险模态分析

一系纵向刚度取5 MN/m，等效锥度0.01和0.1时的振动模态以及一系纵向刚度取15 MN/m，等效锥度0.1和0.5时的振动模态如图4，每个模态的计算速度范围为80～570 km/h,步长10 km/h。

图4 不同等效锥度下的振型模态

由图4根轨迹曲线中振型模态的变化可知：随着等效锥度的增大，各振型模态的频率和阻尼发生变化。从振型模态的变化趋势可以看出，在小锥度时整车蛇行失稳是由车体侧滚引起的，且随着等效锥度增加，稳定性逐渐提高，等效锥度对车体失稳模态的频率和阻尼影响减缓；当临界速度达到最大时，引起蛇行失稳的振动模态发生变化，此后驱动摇头导致蛇行运动失稳，且随着等效锥度增大，稳定性逐渐减小；一系纵向刚度5 MN/m时，等效锥度大于0.1后，对驱动模态的阻尼有显著的影响，稳定性迅速下降；一系纵向刚度15 MN/m时，等效锥度大于0.1后，对驱动模态阻尼的影响微小，稳定性下降缓慢。