基于局部特征子结构方法的连续结构优化
2018-09-08毛虎平高鹏飞秦健健
毛虎平,高鹏飞,秦健健
(中北大学 机械与动力工程学院,山西 太原 030051)
0 引言
大型连续结构优化的难度非常大,主要表现在两个方面:①大型连续结构有限元分析非常耗时,造成寻优过程效率低下;②杆单元、平面单元、梁单元等这些简单单元常以单元截面积、单元厚度和梁截面积为设计变量,很容易实现,而连续结构不具备这些特点,因此其参数化比较困难。根据子结构方法的优势与优化过程中各个子功能的特点重新进行优化是一种有效的解决方案。
采用一般有限元法求解大型复杂结构时,常常遇到计算机容量不足或所需机时过长的问题。为克服这类困难,采用位移子结构法研究平面问题,在满足子结构内节点处平衡条件和相容条件的情况下,综合各子结构的受力与变形,将庞大的原结构划分为若干子结构来计算[1]。主模态叠加法是特殊的Ritz向量,其仅反映结构自身的动力特性,而与结构所承受的动力载荷无关,因此在确定结构对外部动态载荷的响应时,无法事先知道哪些Ritz向量的贡献是主要的,也就无法事先决定该取多少Ritz向量进行叠加比较合适。Wilson提出了Ritz向量直接叠加法,其中Ritz向量的选择不仅与结构自身的动力特性有关,还与结构所承受的载荷空间分布性态相关联,在此基础上,楼梦麟[2]提出了结构动力分析的静态子结构法。
对汽轮机零部件进行有限元分析时,存在有限元形成的线性代数方程组阶数高的问题,例如对成组叶片的强度分析可以达到几千阶方程组,因此求解时首先考虑计算机的容量和速度问题。郑鑫元[3]研究了大型结构问题的静态和动态子结构方法;李元科等[4]采用子结构的思想,将高阶刚度方程简化为低阶凝聚方程,由接触点位移与力的关系引入接触边界条件,最后计算了滚动轴承的有限元分析。在求解灵敏度的分解法中,更关心的是子问题之间的位移耦合信息,子问题间的应力约束耦合取决于位移耦合,基于这一点,兆文忠等[5]从结构分析的子结构概念出发,提出位移敏度分析子结构法进行子结构技术的深入研究。
拓扑优化以单元为拓扑变量,对于大型结构,拓扑变量随着单元数的增多而增多,会导致求解困难。借助子结构的思想,可以将复杂结构分解为多个子结构,分别进行优化,最后达到优化整体结构的目的[6]。为了得到不同内力载荷需求的传力路径,可以基于子结构法将结构分开,使内力暴露出来,然后以结构质量最小为目标,以内力为约束建立拓扑优化模型,基于独立、连续、映射方法和单位载荷法将内力显式化,通过累加获得需要控制的传力路径上的内力,通过迭代调整各路径上的内力使其比值达到一个稳定的值,从而获得满足内力约束的传力路径[7]。传统的拓扑优化方法在整体求解寻优过程中不能控制特定区域的材料分布,舒磊等[8]提出复合域拓扑优化方法,即在不同区域指定不同数量的材料,以改善汽车或设备在不同工作环境下的需要。
为了解决数值子结构与试验子结构的边界协调耦合问题,降低子结构之间的依赖性问题,可根据各个子结构的特点选用专用的有限元软件进行分析或试验。江浩然等[9]提出界面单元子结构协调方法,通过对子域引入边界力并建立边界上的平衡关系和位移协调关系,使界面单元可以耦合多个子结构,但子结构边界上的节点不用完全对应。也可以定义一个虚拟单元集合,该集合拥有有限个虚拟节点,而虚拟节点与实际节点可以不对应[10],同样能够解决界面单元耦合多个子结构的难题。汪博等[11]根据阻抗耦合子结构法的基本原理,给出基于阻抗耦合子结构法求解电主轴固有特性的流程。
针对大型结构精确灵敏度直接分析方法求解时间长的问题,张保等[12]通过重新排列节点,将与设计变量有关的节点位移排到总位移列阵的后面,按重排后的顺序投放刚度矩阵,然后对其进行区域分块,并聚缩得到子结构矩阵,显著提高了效率。子结构方法能够将很高阶数的线性方程组转化为低阶方程组,采用凝聚、降级、分阶段的方法进行求解,可满足大型复杂结构有限元分析的需要[13]。由于客车有限元模型的单元数量比较庞大,使拓扑分析需要耗费大量的计算机时和人力资源,张帆等[14]在某空气悬架客车的拓扑优化分析中引入子结构法,将不需要进行拓扑优化的部分通过矩阵凝聚生成超单元,将待优化部分与超单元连接建立拓扑模型,极大地减少了模型的单元数量。
在结构动态优化设计中常有多个设计参数,每个变量参数的变化对结构性能的影响不同,如何选择对结构动态特性影响最灵敏的变量作为调整的主参数,对于提高结构动态特性具有十分重要的意义,然而庞大的分析量和机时在实际操作中会带来极大的困难。为此,张灶法等[15]提出一种便捷有效的基于应力值的静态灵敏度分析子结构法。动态子结构法的基本原理建立在振型叠加法基础上,仅适合于求解线性结构的动力问题,限制了动态子结构法在非线性结构体系的应用,王菲等[16]提出适用于非线性子结构与多个线性子结构边界耦合的模态综合方法,将整体体系划分为线性和非线性两类子结构,对线性子结构按照势能判据截断准则进行自由度缩减,最终与非线性子结构进行综合获得非线性体系的动态响应。丁晓红等[17]针对复杂机械系统中因构件的边界条件难以确定而不能得到最优结果的问题,基于子结构法,根据力的传递路径确定构件所承受的载荷,以保证构件边界条件的准确性,并通过逐步逼近优化最终得到构件材料分布的拓扑形态。钟薇等[18]针对复杂离散结构优化中设计变量多等问题,提出基于子结构法的分解协调策略,并给出结构分析协同优化框架,将复杂的结构优化问题转化为多个并行、独立的子结构优化问题。
通过文献分析可以看出,子结构方法已经应用于拓扑优化等各个工程技术领域,其本身也得到了快速发展,然而缺乏利用子结构法进行大型结构优化的通用性研究。基于此,本文提出一种基于局部特征子结构划分的连续结构优化方法,采用3类局部特征不同的子结构分别承担优化过程中的3类功能,每一类子结构均会改善优化过程中不同子功能的性能,从而使总体优化具有高效性和收敛性。
1 连续结构优化问题描述
本文研究的对象是连续结构(如柴油机活塞等)在允许的应力和位移约束下使结构质量最小化的问题。优化模型如下
minW(X)。
s.t.
|σ|max(S,X)≤σu;
|d|max(S,X)≤du;
K(X)U=F。
(1)
式中:W为整体结构质量,X为设计变量向量,S为状态变量向量,|σ|max(S,X)为结构绝对最大应力,σu为允许的应力上限,|d|max(S,X)为结构绝对最大位移,du为允许的位移上限,K(X)为总刚度矩阵,U为节点位移向量,F为力向量。
目前优化方法分为两大类:第一类是基于梯度的优化方法,如序列二次规划法(Sequential Quadratic Programming, SQP)等;第二类是现代优化方法,如遗传算法(Genetic Algorithm, GA)等。基于梯度的优化方法又分为约束优化和无约束优化,绝大部分工程问题均为约束优化,其求解可采用第一类优化方法,也可采用第二类优化方法。与现代优化方法相比,基于梯度的优化方法具有仿真次数少、效率高的特点,因此在连续结构优化中通常采用基于梯度的优化方法。然而,因为工程问题大部分为基于仿真的优化,即求解目标函数和约束函数均需要进行大型计算(如有限元分析),所以梯度计算一般采用中心差分法,这种方法求梯度的仿真次数为2n+1次(n为设计变量个数),结构仿真耗费时间较多,因此可以从结构仿真出发考虑采用更先进的方法来提高效率。子结构法是目前提高结构仿真效率的有效方法之一。
2 子结构法
子结构法是将一组单元用矩阵凝聚为一个超单元的过程。超单元的使用方法与其他单元一样,不同的是超单元能够节省大量计算时间,在计算机资源有限的情况下解决大规模问题,从而提高效率,特别是在含有反复迭代的各种动力学分析、非线性分析和优化分析中更能显示其无比的优越性。处理子结构之间的耦合问题常采用子结构综合法,该方法分为固定界面模态综合法和自由界面模态综合法两类。本文拟采用子结构综合法,子结构的划分原理如图1所示,图中沿着虚线将整体结构划分为2个子结构I1和I2,虚线B为每个子结构与其他子结构相邻的边界,其上的节点为连接节点,其余节点为内部节点。
一般结构静力学分析的整体有限元控制方程为式(1)中约束函数的最后一个等式。首先将其分解为子结构和子结构之间的界面两部分,即
(2)

(3)

(4)
(5)
求解式(3)可得子结构边界位移,将其分别代入式(2)相应的部分即可求出各子结构内部节点的位移。
3 子结构法的实施
子结构法的实施包括以下6部分:
(1)确定子结构部分 将需要优化的连续结构划分为两大类子结构:①既不包含状态变量,也不包含设计变量的子结构;②包含状态变量或设计变量的子结构。前一类需要运用子结构方法,后一类不用子结构方法。
在优化过程中,第一类子结构的几何结构不变,第二类子结构又可分为两类:①参数化子结构,指包含有设计变量的局部结构;②状态变量子结构,指包含有状态变量的局部结构,即约束函数或目标函数中含有的状态变量,但又不是设计变量。在一个结构中,参数化子结构和状态变量子结构都可以有多个。有时参数化子结构不仅包含设计变量,还包含状态变量,但状态变量子结构只包含状态变量。
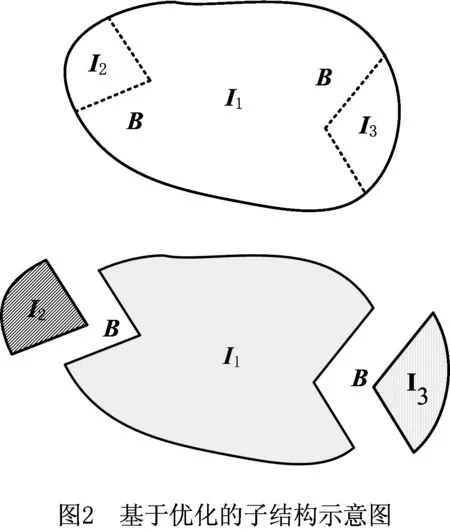
如图2所示,整体结构分为3个子结构Ii(i=1,2,3);B构成每个子结构与其他子结构相邻的边界,其上的节点为连接节点,其余节点为内部节点。I1是第一类子结构,其在优化过程中的几何结构不变,而且既不包含设计变量,也不包含状态变量;I2,I3是第二类子结构,其中I2为参数化子结构,I3为状态变量子结构。
(2)选择主自由度 主自由度包括:①与非超单元的接触部分的所有节点;②约束条件对应的所有节点;③施加载荷的所有节点;④任意节点(这些节点的选择与精度有关系)。一般结构仅选择①②③作为主自由度即可,在某些特殊情况下除了①②③作为主自由度之外,还要考虑④相关的主自由度。
(3)将不同的子结构分别生成超单元 根据式(2)~式(5)将每个子结构进行矩阵缩减,大大缩小了整体组装后的矩阵规模。
(4)耦合超单元与非超单元 超单元是连续结构中既不包含状态变量,也不包含设计变量的部分。几何结构在优化过程中不会改变,如果在优化前对超单元进行网格划分并施加边界条件,则优化时可以直接使用,从而节省大量时间。非超单元是连续结构包含设计变量或设计变量的部分,这部分又分为两种:①包含设计变量的同时,也可能包含状态变量,对这部分子结构进行网格划分并施加边界条件需要实时进行,最重要的是超单元与非超单元之间的连接部分,即公共部分,以超单元所对应公共部分的节点为初始条件划分非超单元,然后将两种结构对应的公共面节点耦合起来;②只包含状态变量,与超单元子结构的处理方式类似,这部分子结构的几何结构在优化过程中不会改变,因此在优化之前将这部分子结构进行网格划分并施加边界条件,然后与超单元子结构耦合,在优化过程中直接应用,也可节省大量时间。利用状态变量子结构的目的是避免每次完成仿真后对超单元进行扩展,从而极大地提高计算效率。
(5)求解 耦合后的结构整体矩阵规模远小于非子结构整体矩阵,可用高斯消元法求解。一般在一个连续结构中,超单元子结构所占比例总是远远大于状态变量子结构和参数化子结构,因此子结构的应用可以大大减小计算规模,提高计算效率。
(6)扩展 扩展需要耗费时间,对于需要反复求解的问题,可以将扩展放在最后进行,例如优化过程中需要反复求解结构有限元模型,扩展仅用于优化结束时的验证分析。应用状态变量子结构就是为了避免进行子结构扩展计算,从而节省大量时间,提高效率。
4 基于子结构法的优化迭代
优化过程如图3所示。图3a为划分子结构时,状态变量不是单独在一个子结构中,而是包含在参数化子结构中,这样可以省去构造状态变量子结构。图3b为一般的优化过程,包括超单元子结构、状态变量子结构、参数化子结构3部分,前两部分对应的有限元模型只需生成一次,在迭代过程中与最后一部分耦合参与整体模型求解,求解完成后,从状态变量子结构中提取状态变量值,从参数化子结构中提取所状态变量值,然后将所有状态变量的值和参数化子结构的设计变量初值返回优化器,通过优化器分析计算后决定下一组迭代的设计变量值。参数化子结构在优化过程中需要实时生成几何结构、划分网格、施加边界条件以及耦合与其他子结构的接触边界,即利用新设计变量值重新生成参数化子结构,这样反复迭代直至收敛。

图3中没有扩展这一步,是因为从优化的角度划分子结构时,已经进行了充分考虑。因此将整体结构划分为3种类型子结构,即超单元子结构、状态变量子结构和参数化子结构,优化过程中仅从状态变量子结构和参数化子结构中获取目标函数和约束函数所需的状态变量值即可,因此不需要对超单元子结构进行扩展。
5 柴油机活塞设计实例分析
某柴油机活塞主体材料的弹性模量为7.0×106Pa,泊松比为0.3,镶圈材料的弹性模量为11.0×106Pa,泊松比为0.33,几何尺寸和形状如图4所示。为了说明子结构法的优越性,以活塞质量最小为目标函数、油腔形状为设计变量进行优化。

本文建模时没有考虑气缸,因此忽略侧推力、摩擦力对活塞的影响。机械应力主要由最大爆发压力和活塞惯性力作用生成。缸内压力的施加情况如图5所示,结合活塞的实际受力情况,将缸内压力pj按均布力施加在活塞顶面,并以一定比例分别施加在各环槽和环岸。活塞往复惯性力由活塞加速度曲线得到。因为采用1/4有限元模型进行静力学分析,所以在对称面上施加对称约束,在活塞销座上施加全约束。当进行静力学分析时,考虑最大爆压时刻活塞的受力情况,采用本文方法将活塞根据前期试算应力分布划分为3个子结构,分别为超单元子结构、状态变量子结构和参数化子结构,然后进行网格划分,如图6所示。


有限元仿真计算是基于结构的三维实体模型进行的,在保证仿真计算精度的前提下,为降低计算时间,采用1/4活塞组合模型作为有限元计算模型,并采用Solide45单元进行网格划分。初始活塞计算所用的有限元模型网格如图6所示,该模型包括123 011个四面体单元和24 695个节点。在图6a中,前两个图是几何结构,为超单元子结构、状态变量子结构和参数化子结构的不同部分,后两个图是生成3个子结构的有限元网格模型。柴油机活塞优化模型:
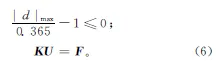
柴油机活塞的子结构优化方法如图3b所示。优化器采用MATLAB优化工具箱中的fmincon函数,并结合有限元求解器进行优化。对于柴油机活塞来说,经过前期试算,发现约束函数需要的状态变量并不包含在参数化子结构中,因此需要独立构造状态变量子结构(如图6a),其中柴油机活塞设计变量有5个,如图6b所示。
为了说明本文方法的有效性,并排除初始值对结果的影响,在设计域内任意取5个点作为初始值进行优化。初始值选择和优化结果如表1所示,5组初始值的优化迭代过程如图7所示,第5组初始值优化的结果验证如图8所示。
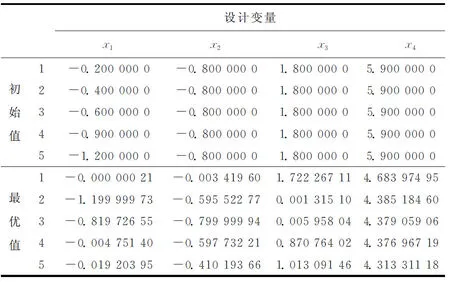


从图7、图9和表1~表4可以看出,初始值不同,最优值也不同,这是由局部优化导致的,而且由目标函数和约束函数组成的设计域所构成的函数是一个黑箱函数,可以确定一个多峰值函数,要获得全局最优解,需要全局优化求解器,然而目前全局优化求解器(GA、模拟退火算法和粒子群优化算法等全局优化算法)的仿真次数非常高,将其直接应用于工程问题求解的成功率很小。与现代优化方法相比,基于梯度的优化方法能接受但为局部收敛,只能从多初始点角度尽可能地获得全局最优。




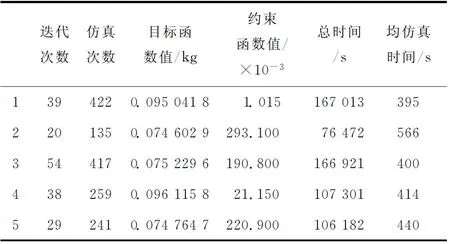
图7所示为柴油机活塞基于子结构法优化的迭代历程,从图7a可以看出其优化过程波动非常大,且波动与图7b对应。从表2可以看出,优化结果均收敛到可行域内,即均满足约束函数,最优函数值为0.099 192 0 kg(这仅为参数化子结构部分),迭代23次,仿真225次,用时54 536 s,平均仿真1次用时242 s/次。在不同初始值的5次优化中,平均用时最多284 s/次,总体平均每仿真1次用时235.6 s/次。图9所示为活塞直接优化的迭代历程,从图9a可以看出其优化过程的波动没有本文方法大,且与图9b也对应。然而从表4可知,最优解均未满足约束函数,即约束函数值均不等于零,最小值为1.015×10-3,目标函数最小值为0.074 602 9,但是其对应的约束函数值为0.293 1。用同样的优化条件,5次优化总体平均每仿真1次用时443 s/次。本文方法用时是传统方法的53.18%,可节省时间46.82%,极大地提高了效率。
本次柴油机活塞优化仅为说明基于子结构法优化的优势,因此对仿真部分做了部分简化,将动态优化简化为静态优化,且未考虑温度载荷。
6 结束语
本文根据优化需要将连续结构划分为超单元子结构、状态变量子结构和参数化子结构,然后将超单元子结构进行缩减,与状态变量子结构或与参数化子结构完全耦合,极大地减小了计算规模,通过空腹梁结构和柴油机活塞优化,说明了基于子结构法的多子结构优化方法非常有效,并获得了以下结论:
(1)局部特征子结构将连续结构在优化过程中承担的主要任务划分为3种子结构,超单元子结构的主要任务是减小仿真计算规模,状态变量子结构的主要任务是提供目标函数和约束函数所需的状态变量值,参数化子结构的主要任务是减小结构重量,也是优化的最终目标。
(2)连续结构总是可以按局部特征划分为超单元子结构、状态变量子结构和参数化子结构,并且超单元子结构包含连续结构的大部分,状态变量子结构和参数化子结构仅占小部分,但结构达到一定规模时,前处理所耗费的时间几乎可以忽略不计。
(3)基于局部特征的子结构优化在3种特征子结构的相互耦合作用下,不但极大提高了效率,而且能很好地收敛。对于某柴油机活塞优化问题(包括123 011个四面体单元和24 695个节点),可以节省时间46.82%,极大地提高了优化效率。
