弧齿锥齿轮铣齿机的主动精度设计

徐彦伟，徐爱军

(1.河南科技大学 机电工程学院，河南 洛阳 471003；2.天津大学 机械工程学院，天津 300072)

0 引言

弧齿锥齿轮是重要的机械传动基础元件，广泛应用于高速、重载相交轴传动[1-2]。弧齿锥齿轮铣齿机，特别是大型数控弧齿锥齿轮铣齿机，是航空航天、航海舰船、武器装备、能源、交通，以及石油、冶金等领域的关键制造装备[3-4]，其精度直接影响弧齿锥齿轮的加工精度和质量，进一步影响影响齿轮副的传动效率、噪声、运动精度和使用寿命等性能。传统的机械结构式弧齿锥齿轮铣齿机传动链异常复杂[5-6]，在一定程度上降低了机床精度。美国格里森公司研制的凤凰Ⅱ系列数控弧齿锥齿轮铣齿机，采用直接驱动电机代替传统机械式弧齿锥齿轮铣齿机中的复杂传动系统，显著提高了机床的传动精度、刚度和加工精度[7-8]，目前处于国际领先地位，但由于技术权益原因，格里森公司一直将其弧齿锥齿轮铣齿机的设计原理和方法作为技术机密。经过多年努力，我国弧齿锥齿轮铣齿机的设计、制造和研发能力已取得了长足发展，但同世界先进水平相比还有一定差距，尤其是在弧齿锥齿轮铣齿机精度设计方面。

精度设计是机械产品设计与制造中的重要环节，是降低机械制造装备加工误差和提高系统精度的重要手段，是一个需综合考虑产品零部件的功能要求、材料性能，以及实际加工能力和加工、装配误差引起的尺寸、形状的变化对产品功能与制造成本的影响，涉及众多因素的复杂综合问题[9-10]。传统精度设计以Ford公司大批量制造中零部件之间的公差配合研究为开端，伴随汽车工业大规模生产方式的出现而快速发展，主要是根据产品的功能要求、装配技术要求等初始约束条件，凭借设计者的经验，参照相关标准、手册，采用极值或概率法，对产品零部件的公差类型、等级和公差数值进行合理设计，以确保将零部件的制造精度限制在一定范围内，在机械产品的研究及发展过程中发挥了重要作用；但传统精度设计方法效率较低且存在不确定性，很难达到统筹全局、降低成本、提高产品性价比的效果。计算机辅助精度设计将传统精度设计方法和计算机技术相结合，在机械产品的设计、加工、装配、检测等过程中，利用计算机对机械产品及其零部件的尺寸和公差进行并行优化与监控，力图用最低成本设计、制造出满足用户要求的产品，有效地提高了机械产品精度设计的效率[11]。然而，传统精度设计和计算机辅助精度设计都属于常规精度设计，考虑制造装备加工对象的精度要求相对较少，特别是弧齿锥齿轮这类复杂空间曲面零件的加工精度要求，由于制造装备精度与零件加工精度不存在简单对应关系，缺少制造装备精度与加工对象精度之间映射关系的数据资料，使得常规精度设计方法较难适应弧齿锥齿轮铣齿机这类复杂制造装备的精度设计，可能会导致精度设计过剩，造成成本剧增，降低了产品性价比，或者精度设计不足，导致零件的实际加工精度不能满足产品的功能需求。查阅文献[12-15]，鲜见针对弧齿锥齿轮铣齿机这类复杂制造装备的精度进行合理设计的有效方法，这已成为制约我国弧齿锥齿轮制造装备技术进步的瓶颈之一。

为合理设计弧齿锥齿轮铣齿机的精度，本文从弧齿锥齿轮的加工精度要求出发，研究面向零件加工精度要求的弧齿锥齿轮铣齿机主动精度设计方法，以期实现制造装备精度设计的按需“定制”。数控机床最关键的技术指标是数控运动轴的重复定位精度，为简化问题，本文假设机床的热变形、弹性变形、几何误差及安装误差、工件几何误差和机床运动轴的系统误差已予以修复，主要研究弧齿锥齿轮铣齿机数控运动轴的重复定位精度。

1 主动精度设计原理

机械精度设计是根据产品的功能要求和经济性确定零部件的公差，以确保零部件的制造误差限制在一定范围内。合理的精度设计是决定产品性价比与设计成功的关键。常规精度设计方法主要是根据制造装备的功能要求，针对传动系统，求解传动链中各零部件的公差，确定各零部件合理的配合精度，是以末端执行机构精度要求为始点、面向“装备”的精度设计。弧齿锥齿轮铣齿机主动精度设计方法则是从零件的加工精度要求出发，求解机床末端执行机构的精度，其基本理念是：通过分析机床的结构及其加工原理，建立弧齿锥齿轮铣齿机数控运动轴定位误差与零件加工误差之间的映射关系——加工误差模型；进一步建立零件加工精度要求和机床数控轴重复定位精度之间的映射关系——加工精度模型；然后，按照等作用误差分配原则，将弧齿锥齿轮的加工精度要求合理地分解为弧齿锥齿轮铣齿机各数控运动轴的重复定位精度。

图1所示为弧齿锥齿轮铣齿机主动精度设计示意图，主要包括误差分析和精度设计两个阶段。在误差分析阶段，首先，建立弧齿锥齿轮齿面模型，通过分析弧齿锥齿轮铣齿机的结构和各数控运动轴的相对运动关系，依据坐标变换将齿面模型表示为机床各数控运动轴的位置参数；然后，建立齿面误差模型，假设其他误差已经修复，主要研究弧齿锥齿轮铣齿机数控运动轴的定位误差，结合误差传递系数Kmi，将齿面加工误差σw表示为弧齿锥齿轮铣齿机各数控运动轴定位误差σi的函数，以研究弧齿锥齿轮铣齿机各数控运动轴定位误差对齿面加工误差的影响。在精度设计阶段，首先，建立齿面加工精度模型，将工件的加工精度要求Tw用工序能力指数Cp和产品特性值总体标准差σw表示，并依据国际标准，按照4σ原则定义数控轴的重复定位精度，再结合齿面加工误差模型中数控轴运动误差的标准差σ，在误差达到精度允许的极值情况下，通过联立方程组消去标准差σ，建立工件加工精度要求和弧齿锥齿轮铣齿机数控运动轴重复定位精度间的映射关系，以研究弧齿锥齿轮铣齿机各数控运动轴定位精度对齿面加工精度的影响；然后，进行精度分配，按照等作用误差分配原则，将弧齿锥齿轮的加工精度要求分解为弧齿锥齿轮铣齿机各数控运动轴的重复定位精度，并确定弧齿锥齿轮铣齿机各数控运动轴重复定位精度的设计规格。

1.1 误差分析

1.1.1 弧齿锥齿轮齿面模型的建立

基于弧齿锥齿轮铣齿机结构和机床数控运动轴布局建立机床坐标系Σm和工件坐标系Σm，根据弧齿锥齿轮产形原理，通过空间坐标转换，将机床坐标系中弧齿锥齿轮切齿刀盘切削刃上的点变换为工件坐标系中齿面上的对应点，即可求得弧齿锥齿轮齿面模型，该齿面模型可以表示为机床数控轴运动参数的函数

rw=rw(xm1,xm2,…,xmn)。

(1)

同理，弧齿锥齿轮齿面的几何参数也可以表示为机床数控轴运动参数的函数

dw=dw(xm1,xm2,…,xmn)。

(2)

1.1.2 弧齿锥齿轮齿面加工误差模型的建立

通常情况下，机床数控轴的运动误差相互独立且服从正态分布，依据误差合成原理[16]，弧齿锥齿轮齿面加工误差Δdw可以近似地表示为机床数控轴运动误差的函数，

(3)

式中Kmi为工件加工误差对机床数控轴运动误差的灵敏度，即误差传递系数。

(4)

式中σi为机床各数控运动轴误差的标准差。

1.2 精度设计

1.2.1 齿面加工精度模型的建立

根据统计学质量控制理论[17]，在已知工序能力指数Cp的前提下，可以用产品特性值总体标准差σw表示工件的加工精度要求：

Tw=Cp×6σw。

(5)

在机床检验通则第2部分——数控轴的定位精度和可重复性测定(ISO 230-2:2006)[18]中，将数控机床运动轴的重复定位精度Ri表示为

Ri=4σi。

(6)

联立式(4)～式(6)可得齿面加工精度模型为

(7)

1.2.2 加工精度分配

按照等作用误差分配原则[16]将工件的加工精度要求向机床各数控运动轴进行分配，灵敏度高度的数控运动轴应分配较小的误差允许值，机床各数控运动轴的重复定位精度与该轴的误差传递系数成反比，满足

(8)

联立式(7)和式(8)可得机床数控运动轴重复定位精度的分配模型为

(9)

2 弧齿锥齿轮铣齿机主动精度设计

2.1 弧齿锥齿轮加工原理

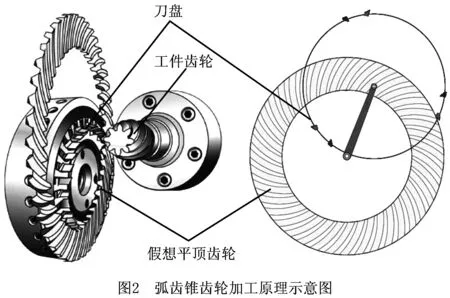
两轴线垂直相交的格里森制螺旋锥齿轮亦称弧齿锥齿轮，广泛应用于直升机、卡车和减速器中，用于传递两相交轴间的转矩。弧齿锥齿轮通常依据“假想平顶齿轮”原理进行加工[4-6]。在传统机械结构的弧齿锥齿轮铣齿机中，假想平顶齿轮与机床的摇台同心，铣齿刀盘偏心地安装在铣齿机摇台上并与摇台一起摆动，铣齿刀盘的切削面形成假想平顶齿轮(产形轮)与工件齿轮相啮合的一个“齿”。铣齿过程中，假想平顶齿轮与工件齿轮毛坯按照设定的速比绕各自的轴线转动，做无隙啮合，刀盘切削刃逐渐在工件齿轮的毛坯上加工出齿形。摇台摆动一次，铣齿刀盘在工件齿轮的毛坯上加工出一个齿槽，然后摇台反转，回到初始位置，同时工作台亦后退，工件齿轮毛坯转过分齿角度，完成单个切齿循环。重复上述运动加工下一个齿槽，反复进行即可加工出整个齿轮。图2所示为依据“假想平顶齿轮”原理加工弧齿锥齿轮的加工原理示意图[7]。

2.2 数控弧齿锥齿轮铣齿机加工坐标系

数控弧齿锥齿轮铣齿机的结构和加工坐标系如图3所示，为了实现依据“假想平顶齿轮”原理对弧齿锥齿轮进行展成加工，铣齿机需具有6个运动轴，即3个转动轴(工件齿轮回转轴A、工件箱回转轴B、刀盘旋转轴C)和3个平动轴(水平方向运动X轴、垂直方向运动Y轴和工作台进给运动Z轴)。

弧齿锥齿轮铣齿机通过X，Y两个平动轴的联动控制切齿刀盘中心在机床坐标系中的瞬时运动位置，模拟假想平顶齿轮的转动，通过X，Y，Z，A，B五轴联动控制工件齿轮与切齿刀盘在机床中的瞬时相对位置，使产形轮与工件齿轮的运动满足弧齿锥齿轮展成加工所需的约束条件，实现弧齿锥齿轮展成加工。

图3中：Om为机床床身坐标系原点或机床中心点，与刀尖平面和产形轮轴线的交点重合；Oc为产形轮坐标系原点，与点Om重合；Ok为刀盘坐标系原点；Ow为工件齿轮坐标系原点，位于工件齿轮的设计交叉点；Σm为机床床身坐标系OmXmYmZm，与机床床身固连；Σc为产形轮坐标系OcXcYcZc，与产形轮固连；Σk为刀盘坐标系OkXkYkZk，与刀盘固连；Σw为工件齿轮坐标系OwXwYwZw，与工件齿轮固连；q0为角向刀位，即产形轮坐标系原点、刀盘坐标系原点连线与床身坐标系Xm轴之间的夹角；Sr为径向刀位，即产形轮坐标系原点与刀盘坐标系原点之间的距离；δm为工件齿轮安装角；E为垂直轮位，即工件轴与产形轮轴之间的距离；Xb为床位，即工件箱相对标准位置沿产形轮中心线方向前进或后退的距离；Xp为轴向轮位，即沿工件齿轮轴线，由工件齿轮设计交叉点到过产形轮中心线竖直平面的距离；加工弧齿锥齿轮时垂直轮位E等于零。

2.3 弧齿锥齿轮齿面模型

图4所示为展成法加工螺旋锥齿轮大轮的切齿加工示意图[5]，图中：M为刀盘切削刃面上任一点，M0为MOk截面上的切削刃刀尖顶点，r0n为切削刃刀尖顶点半径(下标n=a表示外切削刃，n=b表示内切削刃)，q为刀位角，θ为M点的相位角。切削刃刀尖顶点M0在床身坐标系Σm中的位置矢量为：

rM0=OmM0=[Srcosq+r0nsin(q-θ)]i+

[Srsinq-r0ncos(q-θ)]j。

(10)

对于坐标轴式弧齿锥齿轮铣齿机，刀盘中心位置由X和Y轴坐标决定:

(11)

(12)

刀盘切削刃锥面上M点的单位法矢n，以及过M点沿切削锥面母线方向的切向单位矢量t在床身坐标系Σm中分别表示为：

n=±cosαn·sin(q-θ)i±cosαn·

cos(q-θ)j-sinαnk;

(13)

t=±sinαn·sin(q-θ)i±sinαn·

cos(q-θ)j+cosαnk。

(14)

n=a时“±”取“+”，n=b时“±”取“-”。

令|MM0|=μ，则刀盘切削刃面上M点在机床坐标系中的位置矢量，即假想平顶齿轮的齿面方程可表示为

rc=OmM=rM0-μt。

(15)

令m2=OwOm，则有

m2=-Xpp-Ej-Xbk。

(16)

设点M为产形轮齿面与大轮齿面的共轭接触点，其相对于大轮设计交叉点Ow的位置矢量，即大轮齿面方程可表示为

r2=OwM=rc+OwOm=rM0-μt+m2。

(17)

在共轭接触点M处，产形轮齿面与大轮齿面的相对速度v(cw)与公法线n垂直，即

v(cw)·n=0。

(18)

图4中，单位矢量i,k和p之间满足关系

p=icosδm+ksinδm。

(19)

假设产形轮和工件齿轮之间的滚比为λ，产形轮的回转角速度矢量ωc=k，则工件齿轮回转角速度矢量ωw=λp。在共轭接触点M处，产形轮与大轮的相对角速度ω(cw)和相对速度v(cw)分别表示为：

ω(cw)=ω(c)-ω(m)=k-λp;

(20)

v(cw)=ω(cw)×rc-ωw×m2=ω(cw)×

(rM0-μt)-λp×m2。

(21)

联立方程可得

(ω(cw),rM0,n)-μ(ω(cw),t,n)-λ(p,m2,n)=0。

(22)

由上式解出

(23)

弧齿锥齿轮大轮理论齿面点由该点对应的刀盘中心X,Y坐标和刀盘相位角θ,以及工件齿轮安装角δm、切削滚比λ、刀尖半径r0n、角向刀位q0、刀刃压力角α、垂直轮位E、床位Xb、轴向轮位Xp等加工调整参数确定。对于标准渐缩齿弧齿锥齿轮大轮，大轮的设计交叉点与机床坐标系原点重合，将m2=0代入式(23)和式(17)，可得标准渐缩齿弧齿锥齿轮大轮在机床坐标系中的齿面表达式，通过齐次坐标变换，将其转换到工件坐标系求得齿面方程。

类似于式(1)，通过求解式(17)得到的弧齿锥齿轮齿面方程亦可表示为机床数控轴运动参数的函数

r2=r2(xX,xY,xZ,xA,xB)。

(24)

2.4 弧齿锥齿轮齿面加工误差模型

依据GB 11365-89《锥齿轮和准双曲面齿轮精度》[19]，选取齿距偏差为弧齿锥齿轮的齿面加工误差检验项目，建立弧齿锥齿轮的齿面加工误差模型。

与齿面方程(1)类似，弧齿锥齿轮齿的实际齿距p也可以表示为机床数控轴运动参数的函数：

p=f(xX,xY,xZ,xA,xB)。

(25)

弧齿锥齿轮的齿距偏差Δfpt可近似表示为机床各运动轴的定位误差：

=KmXΔX+KmYΔY+KmZΔZ+KmAΔA+KmBΔB。

(26)

式中Kmi(i=X,Y,Z,A,B)为齿距偏差对各运动轴定位误差的灵敏度。

图5所示为弧齿锥齿轮齿距偏差随机床各数控运动轴定位误差单独作用时的变化规律，弧齿锥齿轮齿距偏差与各数控运动轴定位误差之间基本呈线性规律变化。

联立式(4)和式(26)，可将弧齿锥齿轮齿面加工误差的标准差表示为

(27)

式中σi(i=X,Y,Z,A,B)为弧齿锥齿轮铣齿机各数控运动轴定位误差的标准差。

2.5 弧齿锥齿轮齿面加工精度模型

联立式(5)～式(7)和式(27)，可将弧齿锥齿轮齿面加工精度Twfpt表示为

(28)

式中Ri(i=X,Y,Z,A,B)表示弧齿锥齿轮铣齿机各数控运动轴的重复定位精度。

此即为弧齿锥齿轮的齿面加工精度模型。

2.6 弧齿锥齿轮齿面加工精度分配

合理分配精度在机床设计与制造过程中具有重要的意义，精度不足使机床难以达到零件加工精度的要求，精度过剩则使制造成本剧增[20]。依据等作用误差分配原则，将弧齿锥齿轮的齿面加工精度要求分解为弧齿锥齿轮铣齿机各数控运动轴的重复定位精度。

联立式(8)、式(9)和式(28)，可将弧齿锥齿轮铣齿机各数控运动轴分配的定位精度表示为

(29)

式中|Δfpt|max=Twfpt/2表示弧齿锥齿轮齿距偏差的最大绝对值。

对于给定精度等级的某弧齿锥齿轮，通过建立弧齿锥齿轮齿面加工误差模型，求得弧齿锥齿轮齿距偏差对各运动轴定位误差的灵敏度Kmi(i=X,Y,Z,A,B)，即可依据式(29)求得弧齿锥齿轮铣齿机各数控运动轴重复定位精度的设计值。

3 主动精度设计实例

以YK2275型数控弧齿锥齿轮铣齿机(机床结构如图3)为例，采用主动精度设计方法，对机床各数控运动轴的定位精度进行设计。YK2275型弧齿锥齿轮铣齿机设计加工尺寸范围为100 mm～762 mm，加工精度为6级，工序能力指数Cp=1.67。

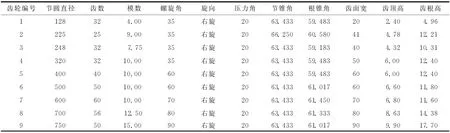
选取6级加工精度、节圆直径为100 mm～750 mm的9个弧齿锥齿轮作为基准齿轮，对YK2275机床各数控轴的重复定位精度进行主动精度设计。基准齿轮的基本参数如表1所示(表中长度单位为mm，角度单位为“°”)，齿距偏差对各数控运动轴定位误差的灵敏度如表2所示，依据GB11365-89得到基准齿轮的齿距极限偏差fpt如表3所示。

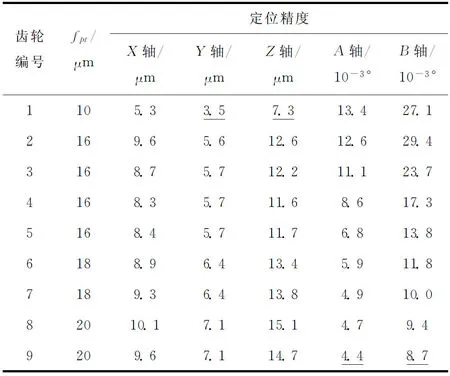
将基准齿轮的齿距极限偏差、齿距偏差对运动轴定位误差的灵敏度、工序能力指数Cp=1.67代入式(29)，可得机床各数控运动轴在加工不同齿轮时所需的重复定位精度(如表3)，每列中的最小值即为YK2275型弧齿锥齿轮铣齿机各数控运动轴重复定位精度的设计值，鉴于X和Y轴的功能等效性，两轴的重复定位精度设计为相同值(如表4)，表中APD+表示主动精度设计，EPD++表示经验精度设计。

按照传统经验精度设计方法得到的YK2275型弧齿锥齿轮铣齿机各数控轴的重复定位精度亦列于表4，以作对比分析。由表4可以看出：按照传统精度设计方法得到的X，Y，Z轴的精度相同，A，B轴的精度亦相同，且设计精度相对较高；按照主动精度设计方法得到的X，Y轴同Z轴的精度不同，A，B轴的精度亦不同，且X，Y，Z，A，B各数控轴重复定位精度的设计结果较传统经验精度设计方法得到的结果经济。

根据表4采用经验精度设计方法得到的数控运动轴重复定位精度，设计、制造了YK2275型弧齿锥齿轮铣齿机样机，对样机数控运动轴的重复定位精度进行测试，并通过加工给定6级精度的基准齿轮，对样机的加工精度进行了验证测试。YK2275型弧齿锥齿轮铣齿机样机数控运动轴的重复定位精度和基准齿轮的基本参数，以及通过样机加工精度测试得到的齿距偏差对各数控运动轴定位误差的灵敏度的测试结果如表5所示。

表5 YK2275样机重复定位精度、基准齿轮基本参数和加工精度测试结果

注：受测试设备功能所限，B轴重复定位精度未进行测量。

将表5中测得的弧齿锥齿轮铣齿机各数控运动轴的重复定位精度，以及齿距偏差对各数控运动轴定位误差的灵敏度，代入式(28)，可以求得工件齿轮加工误差的估计值等于12.4 μm，为齿距误差测量值15 μm的82.7%，基本上可对式(28)进行验证，进而间接验证了弧齿锥齿轮铣齿机数控运动轴重复定位精度分配方程和弧齿锥齿轮铣齿机主动精度设计方法的合理性。

4 结束语

本文面向弧齿锥齿轮的加工精度要求，研究了弧齿锥齿轮铣齿机主动精度设计方法。通过坐标变换建立弧齿锥齿轮齿面方程，选取齿距偏差为齿面误差检验项目，建立了弧齿锥齿轮齿面加工误差模型；采用工序能力指数和产品特性值总体标准差表示零件的加工精度要求，按4σ原则定义数控运动轴的重复定位精度，并结合数控轴运动误差的标准差，建立了弧齿锥齿轮齿面加工精度模型；依据等作用误差分配原则，建立了弧齿锥齿轮铣齿机数控运动轴重复定位精度分配模型。最后，对YK2275型弧齿锥齿轮铣齿机数控运动轴的重复定位精度进行了实例设计和样机精度测试，并与传统经验精度设计方法进行对比分析，结果表明，主动精度设计方法的经济性更佳，有利于提高产品性价比，从而验证了弧齿锥齿轮铣齿机主动精度设计方法的合理性。主动精度设计方法基于分析和建模，可避免经验精度设计的不合理性，提高机床性价比，亦可用于其他复杂机械制造装备。未来的研究应将机床的几何误差以及热、弹变形引起的误差纳入建模。