双层过道布置问题的混合整数规划模型及启发式求解方法
2018-09-08张则强毛丽丽李六柯
管 超,张则强,毛丽丽,李六柯
(西南交通大学 机械工程学院,四川 成都 610031)
0 引言
设施布局问题(Facility Layout Problem, FLP)是以最小化总物流成本为目标,对空间的设施或设备进行组合排序,良好的布局可以有效改善前置时间,提高作业效率,降低成本[1]。据估计,生产过程中总支出的20%~50%用于物料搬运,其中10%~30%的物料搬运成本[2]可通过合理布局来降低。因为该问题具有重要的研究意义和实用价值,近几十年来一直受到工业界和学术界的关注[1-4]。
作为一种特殊的设施布局问题,过道布置问题(Corridor Allocation Problem, CAP)由Amaral[5]于2012年首次提出,并建立了该问题的混合整数规划模型。CAP是将给定数目的设施安排在过道两边,寻求以最小化总物流成本为目标的最优化布局问题。和双行布局问题[6]相似,CAP也具有良好的物料搬运结构与效率,在布局活动中被广泛采用,两者的主要区别在于CAPD必须满足两个条件:①相邻设施之间没有间隙;②上下两行设施的布置起点相同。而双行布局则无需满足[5]。CAP在实际中具有广泛的应用,在服务部门领域,如教学楼中教室及校园管理部门的安排、超市货架沿走廊两边的布置、医院走廊两侧病房和各诊室的安置[7]、行政办公楼过道两边部门的安排[8]、大型购物中心商店的布置等;在工业制造领域,如微电子元器件在集成电路板中的布局、设施沿中心脊柱在凹陷处的布局设计等,其中半导体生产线的布局就是一种常见的脊柱式结构[9]。通过对具有密切联系的部门、元器件或设施设备进行过道布置优化,可进一步提高服务质量、产品性能和生产效率。因此,自2012年提出以来,该问题便快速成为设施布局领域一个新的研究热点[5,7-8,10-13]。
FLP为典型的NP-hard组合优化问题[1],启发式方法是求解该问题的有效方法。Amaral[5]针对CAP提出3种启发式算法,并经大量算例测试验证算法不但有效,而且其求解性能明显优于精确算法。为进一步提高求解效率,Ghosh等[10]应用混合遗传算法和结合路径再连接的分散搜索算法求解该问题,并对小于50个设施规模的算例进行计算,实验结果表明,分散搜索算法在运行效率上较遗传算法更有优势;Ahonen等[11]采用禁忌搜索算法和模拟退火算法对不同规模的测试问题进行了验算和对比,证明在求解质量和求解效率方面模拟退火算法的性能更加优异;Anjos等[12]针对多行布局问题提出一种半正定规划方法,并用小规模算例进行验算,在合理时间内得到了高质量的求解结果,而且针对难度更大的问题,将半正定优化与启发式方法相结合,求得了较高质量的可行解并给出了目标值下界;Hajipour等[14]应用排队系统构建了一种多目标设施位置分配模型,通过算法仿真确定了每层最佳设施和服务分配数量,并验证了模型的有效性;Zhao等[15]应用一种两阶段方法研究不规则形状的物流设施多层布局问题,为物流设施的多层布局提供了一定的参考依据。国内研究方面,李聪波等[16]针对再制造工艺过程的不确定性问题,建立了再制造车间设施动态布局模型,并提出一种基于模拟退火算法的再制造车间设施布局优化求解方法;郑永前等[17]等针对动态单元构建与布局问题中产品需求与机器产能的不确定性,建立了基于模糊需求和机器产能的基本问题模型,并提出一种基于结构化编码的分散搜索算法,通过与LINGO和模拟退火算法进行对比,验证了模型的正确性与算法的有效性。
通过上述CAP相关文献的分析可知,前述工作均是针对单层CAP进行的研究。然而经实际调研发现,当对数量庞大的设施组进行过道布置优化时,过长的通道会增加占地面积,从而增加布局成本。为实现土地的集约利用,降低不必要的成本,设施被迫转向多层空间布置。随着多层布局在实际中被越来越多地采用,研究设施在多层空间中的布局优化越发重要。参考已有文献,尚未发现有关双层CAP的公开报道。
本文考虑生产实际中布局用地成本因素和布置场地受限等情况对过道布置的影响,提出双层CAP,并建立了该问题的混合整数规划模型,通过对28个测试问题进行精确求解,验证了模型的正确性。针对精确方法难以在合理时间内求解大规模问题的不足,提出一种基于C2Opt邻域搜索的启发式算法,应用该算法对所选测试算例进行测试,并与其他3种启发式算法进行对比,验证了所提算法的求解性能。
1 双层过道布置问题模型
1.1 问题描述
CAP是将一系列给定数目的设施布置到过道两侧,寻求一种最优布置,使设施间的总物流成本最小。本文在此基础上考虑用地成本因素、布置场地受限等情况对设施布局的影响,提出双层CAP,该问题的示意图如图1所示。其中,设备组1~3布置在第一层,A~F布置在第二层,各设备组由多台设备组成,共同完成一项作业,可看作为一个“设施”,设备组之间存在一定的物流关系。
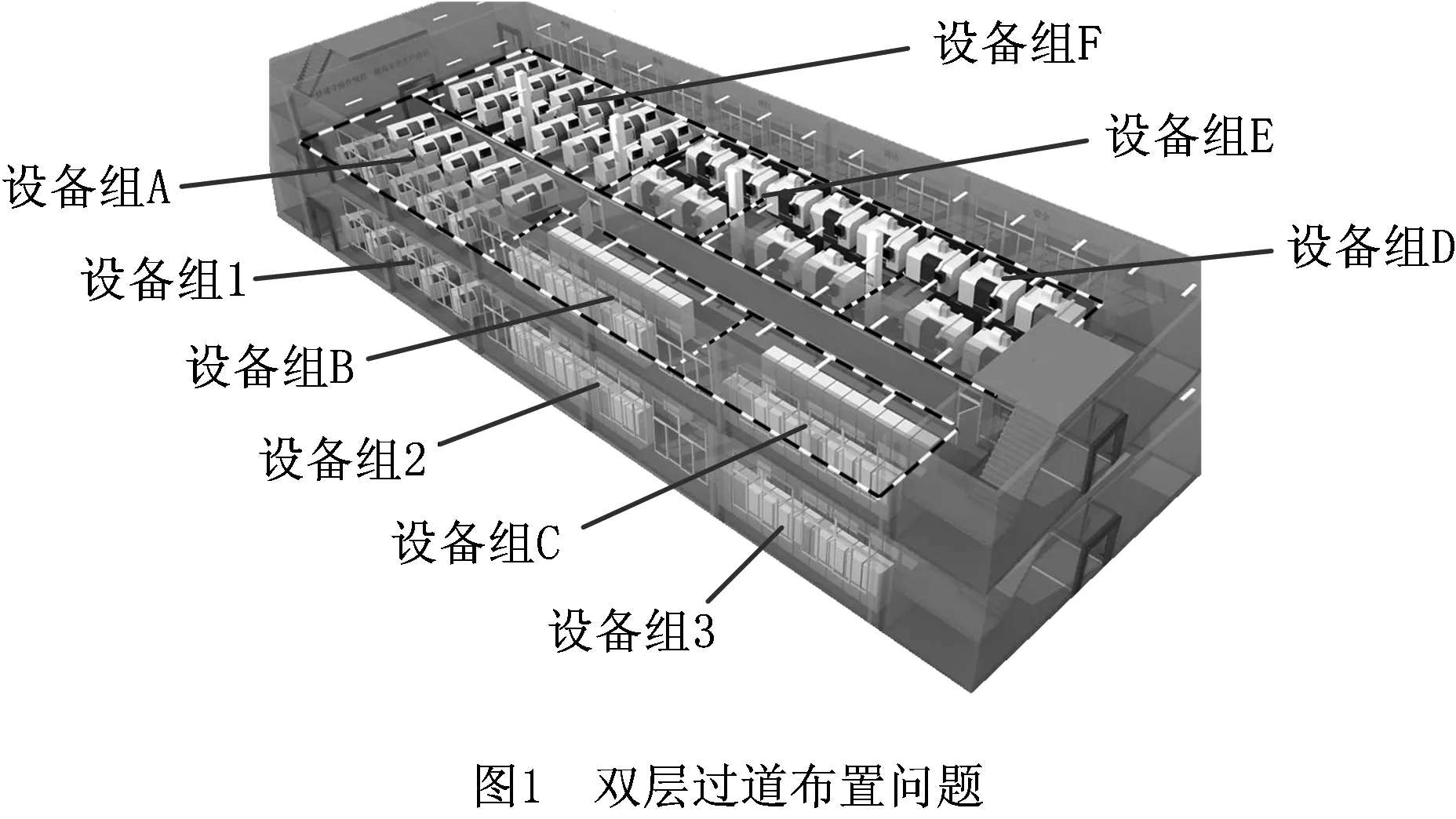
与传统CAP相比,双层CAP的特点为:①设施在两层空间布置,各层设施沿过道两边布置;②不是传统CAP的简单相加,不仅同层设施间存在物流关系,不同层设施之间也存在物流交互,交互通道为放置在过道最左边的货梯。根据该问题的特点,对各层空间中的设施进行组合排序,找到最优布置序列,并确定此时各层设施布置的排列顺序,从而最小化总物流成本。
1.2 基本假设条件
(1)各设施间物流和每个矩形设施靠过道边线的宽度为已知量。
(2)每个设施靠过道边线的中点即为该设施物流的交互点。
(3)相邻两设施之间没有间隙。
(4)各层过道两边设施均从最左边同一点开始布置,并记该点的横坐标为0。
(5)假设每层设施间的通道宽度为0。
(6)不同层设施之间通过货梯进行物流交互,假设货梯长度、宽度为0,只考虑其运输路程。
(7)假设货梯布置在过道最左边,即货梯口与每层过道的布置起点相同。
1.3 变量与参数定义
为描述方便,双层过道布置模型中所用数学符号的意义如下:
P为楼层集合P={1,2};
p为楼层编号,p∈P;
n为问题规模;
Np为第p层所要布置的设施集合;

h为货梯运输路程;
rp,i为设施下标符号,表示布置在第p层的第i个设施,p∈P;
cij为设施i,j之间单位距离的物流成本,∀i∈I1,∀j∈I2,其中I1={1,2,…,n-1},I2={i+1,i+2,…,n};
li为设施i的宽度;
dij为设施i和设施j的设施物流交互点之间的距离;
αij为二进制变量,若设施i,j分配在同一行,且设施i布置在设施j的左边,则αij=1,否则αij=0。
1.4 数学模型
借鉴单层CAP模型,建立了如下双层CAP的混合整数规划模型:
(1)
s.t.
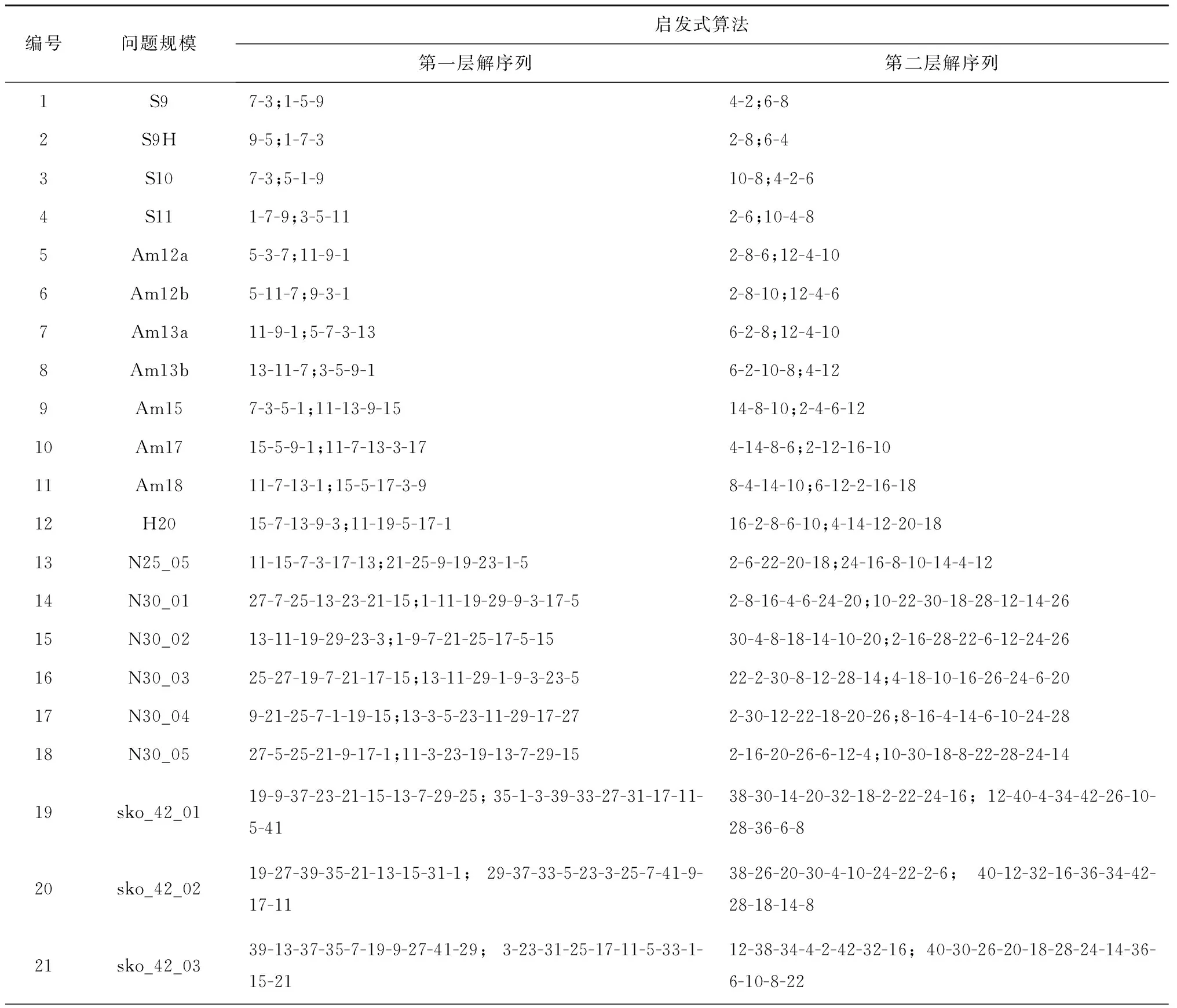
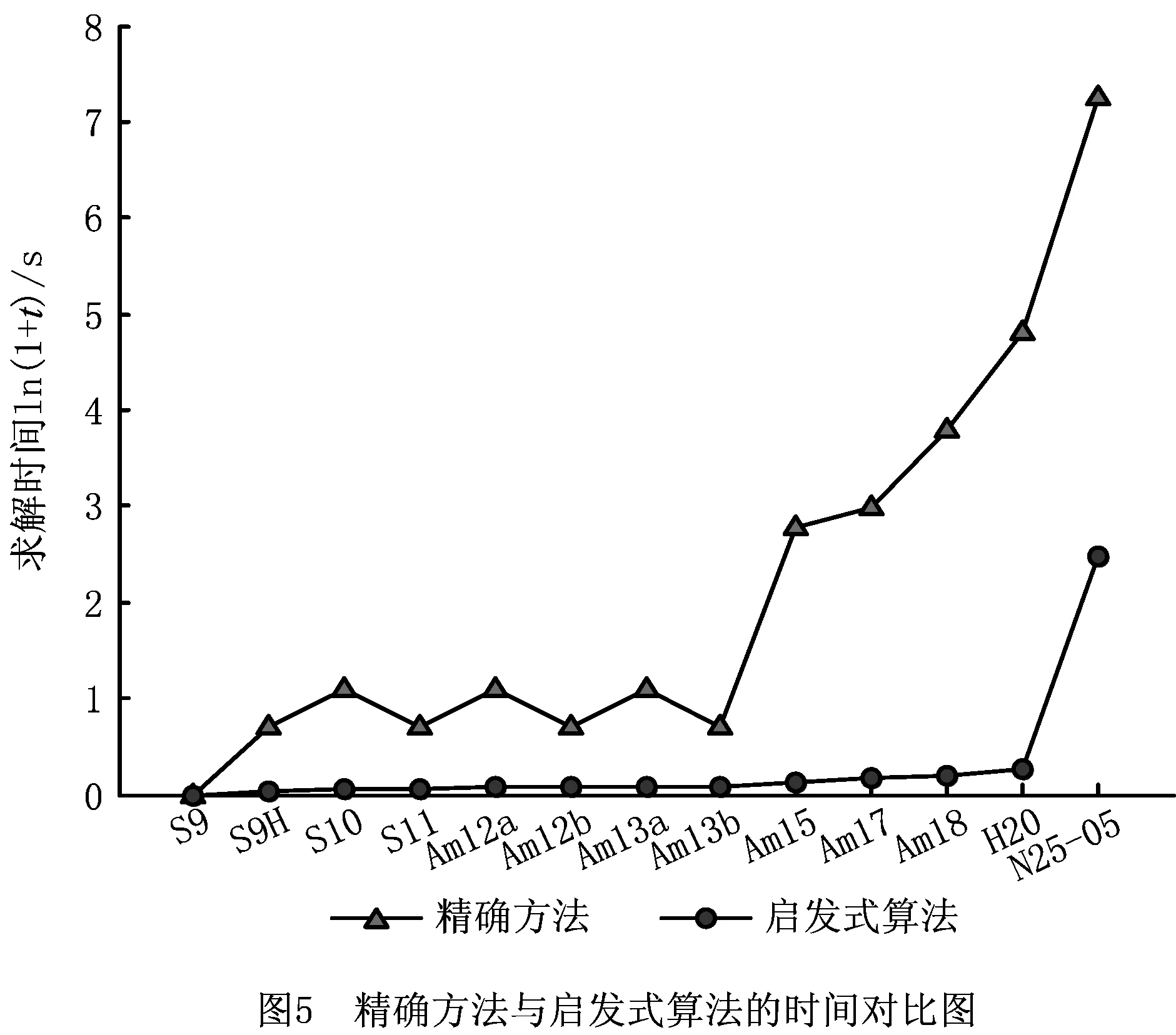
i (2) (3) (4) αrp,jrp,i≥0,i,j∈Np,i (5) -αrp,irp,j+αrp,irp,k+αrp,jrp,k-αrp,jrp,i+αrp,krp,i+ αrp,krp,j≤1,i,j,k∈Np, i (6) -αrp,irp,j+αrp,irp,k-αrp,jrp,k+αrp,jrp,i- αrp,krp,i+αrp,krp,j≤1, i,j,k∈Np,i (7) αrp,irp,j+αrp,irp.k+αrp,jrp,k+αrp,jrp,i+ αrp,krp,i+αrp,krp,j≥1, i,j,k∈Np,i (8) αrp,irp,j∈{0,1},1≤i,j≤n,i≠j,p∈P。 (9) 可知,约束(2)和(3)用于计算同一层各设施间的距离;约束(4)用于计算第一层与第二层各设施间的距离;约束(5)用以防止每层同行设施发生重叠放置;约束(6)~(8)用于确定每层的决策变量αrp,irp,j;式(9)给定决策变量αrp,irp,j的定义域。 双层CAP作为典型的NP-hard组合优化问题,具有较大的求解难度,特别是针对大规模问题,精确方法难以在合理时间内求得最优解,因此本文提出一种启发式算法,以期快速求得高质量的近优解。 结合双层CAP的特点,本文采用一种基于设施的表示方式,通过这种编码方式可将一种布局方案编码成一个设施编号的序列。针对假设(1),首先确定各层所要布置设施的编号,以设施数目n=9的问题为例,一个可行的分配方案为N=[N1;N2],N1={1,3,5,7,9},N2={2,4,6,8},其中N1表示需要布置在第一层的设施编号集合,N2表示需要布置在第二层的设施编号集合。 针对以上确定的分配方案,布局方案中一个可行解的编码和解码如图2所示。 该可行解表示为x=[x1;x2]=[5,3,1,7,9;6,2,8,4],n1=5,n2=4,t1=2,t2=3。其中:n1,n2分别表示布置在第一、二层的设施总数;t1,t2分别表示第一、二层中布置在第一行的设施数。即第一层布局方案x1=[5,3,1,7,9]中布置到第一行的设施数为2,序列为[5,3],第二行序列为[1,7,9];第二层布局方案x2=[6,2,8,4]中布置到第一行的设施数目为3,序列为[6,2,8],第二行序列为[4]。 根据双层CAP的特点,为实现对邻域空间的局部搜索,对原C2Opt的扰动机制加以改进,构建适应该问题的两待交换设施编号选取方法和设施位置互换机制,确保寻优过程中各层所要布置的设施编号不发生变化,且仅当两设施位置交换所得的新序列能对当前较优解做出有益改善时保留计算结果。该C2Opt邻域搜索子程序的具体执行步骤如下: 步骤2令i=1,j=1。 步骤3若i≤n1则执行步骤4,否则转步骤7。 步骤4若j≤n2则执行步骤5,否则i=i+1,转步骤3。 步骤6若V 为避免算法陷入局部最优,本文引入inversion程序,该程序的具体执行过程为:以图2所示的布局方案为例,分别从序列x1,x2中等概率随机选择任意两个不同的设施编号,并倒置这两个设施间的序列,重新排列当前设施序列,具体过程如图3所示。 图中,分别选取设施集合x1,x2中的设施编号5,7与2,8之间的连续序列进行倒置,所得新解为x*=[7,1,3,5,9;6,8,2,4]。 本文所提启发式算法主要包括C2Opt邻域搜索程序和inversion程序,通过不断扰动产生新解序列,扩大搜索空间,最终获得满意解甚至全局最优解。 C2Opt子程序通过交换两个设施位置,产生新的布局序列,若新序列的总物流成本小于原序列物流成本,则保留该交换结果,用交换之后的序列替代原序列,否则放弃交换结果继续下一循环。 针对C2Opt子程序在邻域搜索过程中可能会陷入局部最优而无法求得全局最优解的问题,加入inversion子程序,在C2Opt子程序无法跳出局部最优时,重新随机选择一个新可行解继续搜索。 为避免在搜索过程中遗失当前最优解,在启发式算法执行过程中内嵌一个记忆解OFV,用于保存在邻域搜索过程中找到的最优解,在迭代过程中,当搜索到一个新解[x1′;x2′]时,比较目标函数值ofv和OFV,若ofv 为验证双层CAP模型的正确性,针对设施数目从9~49不同规模的28个基准算例,首先应用Lingo11.0软件进行精确求解,测试数据来源于文献[5,18-22]。计算实验采用的计算机硬件配置为Pentium(R)Dual-Core CPU E6700 3.2 GHz,4 GB内存,在Windows 7操作系统下运行Lingo试验程序求出精确解。 对于所选28个不同规模的基准算例,根据实际中各层布置的设施数相差不大时,占地面积最小的原则,本文假设上下层的设施数均为问题规模的一半,且将设施编号为奇数的设施布置在第一层,编号为偶数的设施布置在第二层。对于本文所提混合整数规划模型,各层布置的设施集合可任意给定,不局限于上述假设情况。 确定各层所要布置的设施集合后,假设货梯运输路程h=10,运用Lingo软件,依据1.4节给出的混合整数规划模型,采用分支定界法进行求解。针对设施数目为9~25的13个中小规模测试问题,Lingo软件在合理时间内求得了最优解,验证了模型的正确性。但随着问题规模的增大,精确方法的求解时间大幅度增加,难以在合理时间内求得大规模问题的最优解。为给所提启发式算法的求解结果提供参考依据,针对规模大于25的测试算例,设置Lingo软件中的运行时间为600 s。 针对精确方法运算时间长、难以求解大规模问题的不足,本文提出一种启发式算法Heuristic_C2Opt,以期在保证求解精度的前提下进一步提高求解效率。为说明本文所提算法求解双层CAP的有效性,将Heuristic_C2Opt算法与文献[5]提出的3种启发式算法进行对比,3种启发式算法分别记为Heuristic_1(2-opt),Heuristic_1(3-opt)和Heuristic_2。随后在同一运行环境下使用MATLAB R2010a软件开发了启发式算法的实验程序。兼顾求解性能与求解效率,经多次运算测试,算法的参数设置如表1和表2所示。通过对传统CAP的研究可知,当过道两边设施数相差不大时,总物流成本最小,由此确定各层布置在第一行设施数的上下限,如表1第5~8列所示。 为准确测试所提启发式算法的求解性能,针对每个测试问题,算法均运行60次,所求得的最优目标函数值OFV及程序运行时间Time/s如表3的第5~12列所示,所得最优解序列如表4所示。 表3 算法求解结果对比 续表3 表4 启发式算法求得的最优设施序列 续表4 将Lingo求得的目标函数值OFV0及程序运行时间Time(单位:s)列于表3中第3,4列,通过对比表3中Lingo和启发式算法的求解结果可以看出,针对13个中小规模的基准算例,Heuristic_C2Opt算法均求得了和精确方法相同的最优解,而其他3种算法未全部求得。对于测试问题N30_01,Lingo11.0软件在求解了69 780 s后仍未找到全局最优解,停止程序运行时所得的当前最优解为10 899,而4种启发式算法所得结果均为10 898,优于Lingo的当前最优解,其中Heuristic_C2Opt算法用时最少。对于所选的28个测试算例,问题规模从9增大到49,精确方法的求解难度呈指数级增长,但Heuristic_C2Opt算法仅在92.99 s的时间内求得了比Lingo运行600 s更好的近优解,且与其他3种启发式算法相比,Heuristic_C2Opt算法也取得了更优结果,由此说明,本文所提Heuristic_C2Opt算法具有优异的求解性能。 Heuristic_C2Opt算法不仅在求解质量上优于其他方法,在求解效率方面亦具有优势。通过对比表3数据可以看出,针对28个测试算例,4种启发式算法中,Heuristic_C2Opt算法在最短时间内求得了最优结果,说明了该算法求解效率的优越性。进一步对比精确方法可知,针对N25_05规模问题,Lingo求得的精确解为13 123,求解时间为1 409 s,而Heuristic_C2Opt算法求得相同解所用的时间为11.02 s,仅为精确求解时间的1/1 193。对于其他大规模算例问题,该算法也在较短时间内求得了高质量的满意解。为更直观地观察该算法的求解优势,针对精确方法与Heuristic_C2Opt算法均能求得最优解的13个中小规模算例,绘制两者的求解时间对比图,如图5所示。 由图5可以看出,针对每个测试问题,Heuristic_C2Opt算法的求解时间均小于Lingo的求解时间,且随着问题规模的增大,精确方法的求解时间大幅度增加,而Heuristic_C2Opt算法的求解时间增长缓慢,表明所提启发式算法具有更高的求解效率。 为进一步表明所提启发式算法的求解性能,根据Heuristic_C2Opt算法求得的1 680个计算结果,计算其与精确方法求解结果的偏差gap, gap(%)=|(OFV1-OFV0)/OFV0|×100%, 并绘制成如图6所示的求解偏差箱形图。图中:箱线图的上下框线、中间线、点画线分别表示该组计算结果的上下四分位数、中位值、平均偏差;上下框线之外的延伸线表示最大值(最小值)到上(下)四分位数的取值区间;符号“+”表示不在正常值分布区间的异常值。可以看出,针对28个不同规模的基准算例,方盒长度普遍较小,特别是对规模小于15的测试问题,其上、下四分位数几乎与中位值重合于0,偏差gap的最大值也仅为0.16%,表明所提启发式算法具有良好的求解稳定性。 通过分析表3中的数据可以看出,Heuristic_C2Opt算法可以快速求得近优解,尤其对于中小规模测试问题,所用求解时间均不足1 s,对于大规模问题也能较快求解,具有较高的求解效率。为进一步说明该启发式算法的求解特点,选取N25_05,N30_05,sko_42_05和sko_49_05 4种不同规模的测试问题绘制相应的算法收敛图,如图7所示。 由图7可以看出,4条收敛曲线的下降趋势明显,说明所提启发式算法具有较快的收敛性,且算法在搜索过程中具有跳出局部最优的能力。为进一步说明算法的收敛速度,以测试问题N25_05为例,当算法进行到第323次迭代时,寻得最优目标函数,相当于算法运行1.41 s后就已经找到近优解13 123,由此可见该启发式算法收敛速度快,具有较强的搜索性能。 针对实际布局活动中对多层过道布置的需求,本文构建了考虑设施空间布局的双层CAP,建立了该问题的混合整数规划模型。为求解该问题,提出一种基于C2Opt邻域搜索的启发式算法。该算法主要由改进的C2Opt邻域搜索程序和inversion程序构成,通过引入的记忆机制保留精英解。运用Heuristic_C2Opt算法对28个不同规模(9~49个设施)的基准问题进行测试,并与3种启发式算法进行对比,结果表明Heuristic_C2Opt算法在求解质量和求解效率方面均优于Heuristic_1(2-opt/3-opt)和Heuristic_2算法。而且对于中小规模问题,启发式算法能求得和精确方法相同的最优解,求解时间不超过1s;对于大规模问题,所提算法的求解结果优于给定时间内Lingo的精确求解结果,且随问题规模的增大,其求解优势愈加明显。 由于双层CAP具有较高的复杂性,本文在假定分配方案已知的前提下进行了研究,下一步将考虑对所有可能的分配方案进行布置优化,并将用地成本融入目标函数,进一步完善双层CAP。在求解方法层面,将寻求更加优异的智能算法,进一步提高搜索效率与求解质量。
2 启发式算法
2.1 解的编码和解码表示
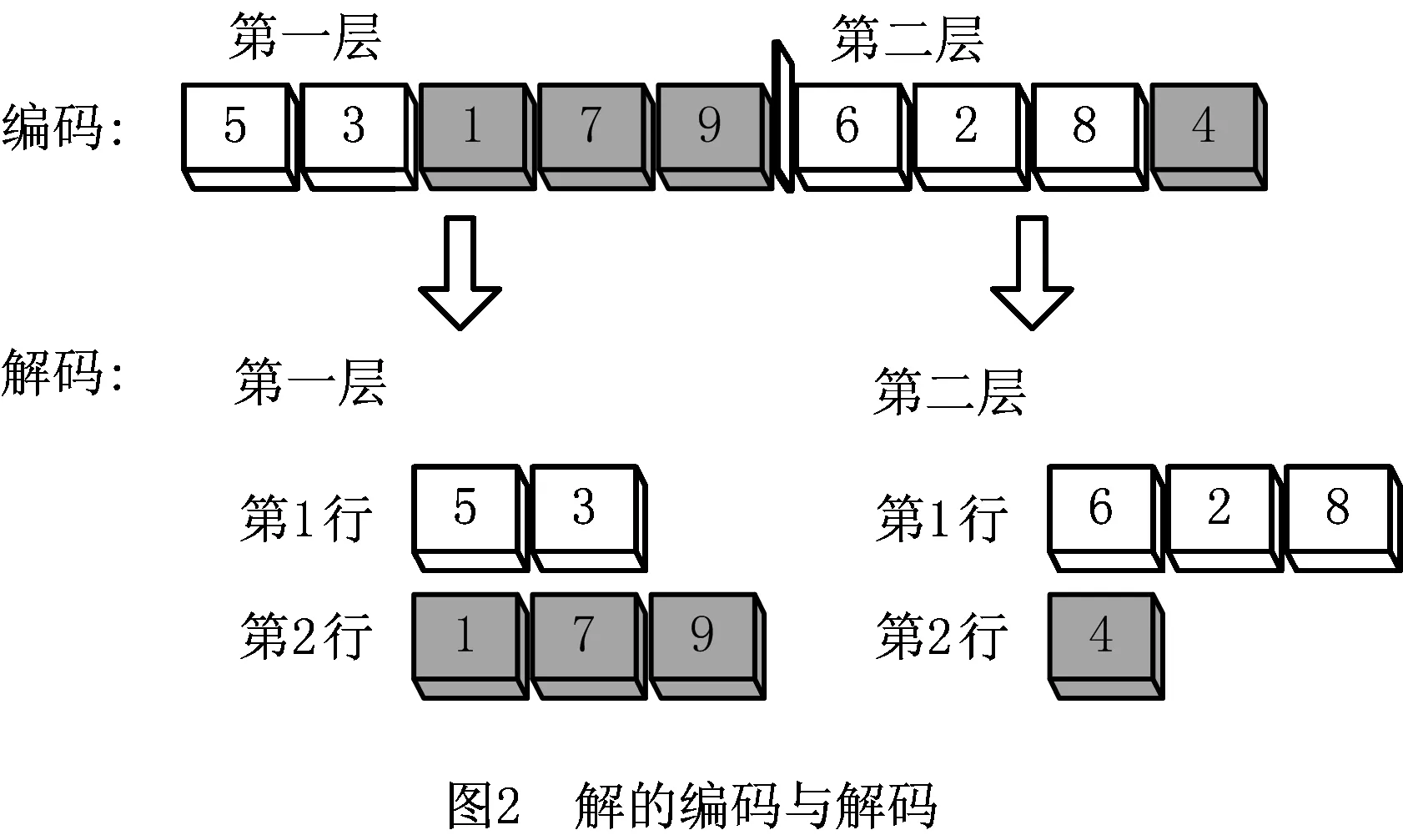
2.2 C2Opt邻域搜索程序与inversion程序

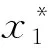
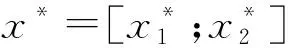

2.3 算法步骤
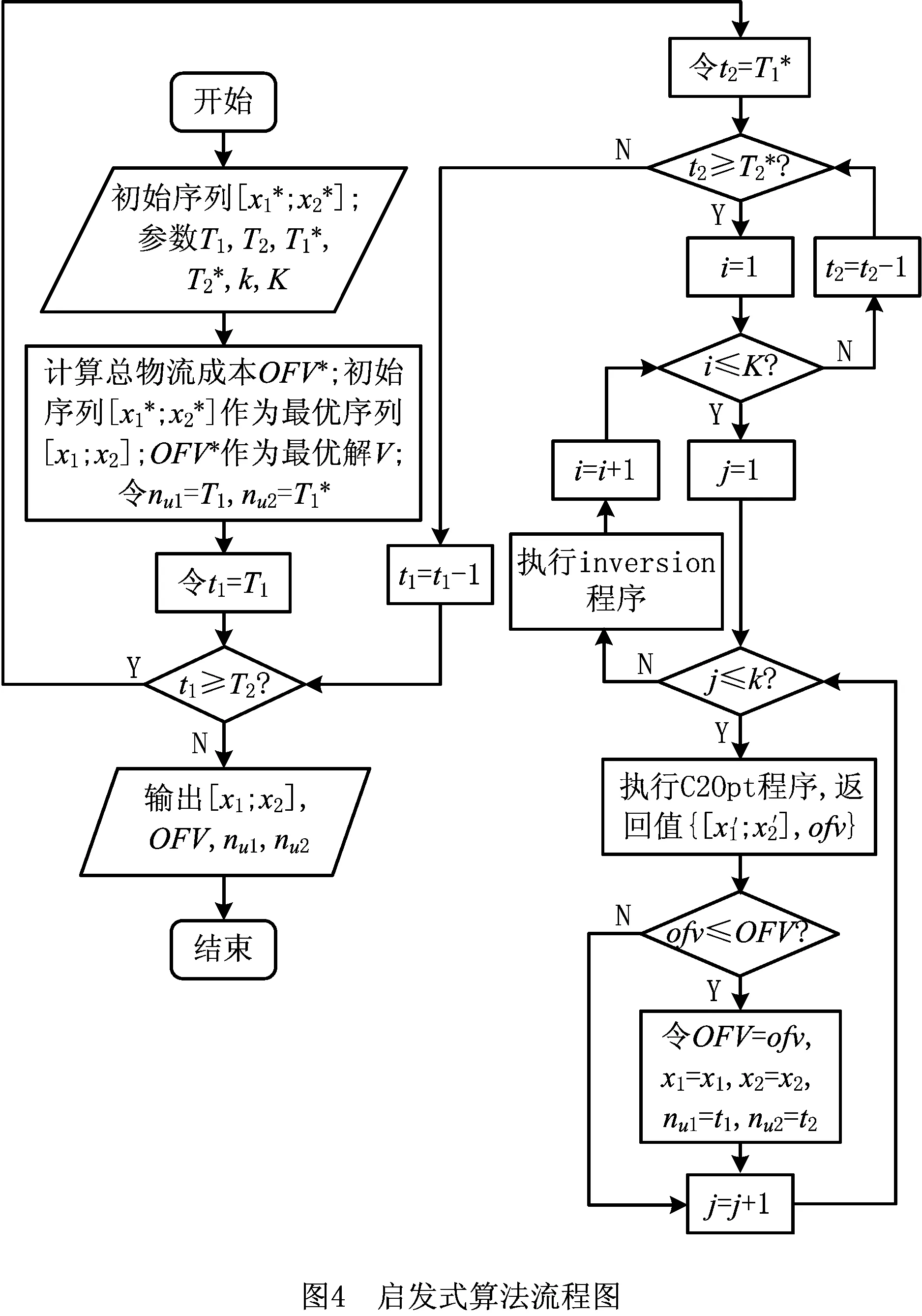

3 实验结果与分析








4 结束语
