轻量化蜂窝3D打印路径自适应生成技术

孙登广，戴 宁，黄仁凯，张 敏，孟令尹，张 壮

(南京航空航天大学 机电学院，江苏 南京 210016)

0 引言

增材制造技术的快速发展促进了产品轻量化技术的广泛研究与应用，然而由于缺乏相应力学理论的研究，导致轻量化产品存在材料损耗严重、承载能力不足等问题。现有轻量化3D打印路径技术尚难以兼顾力学特性和模型轻量化设计，因此研究构建满足特定材料消耗和应力分布的轻量化打印轨迹具有重要的实际应用价值。

基于3D打印技术的轻量化方法主要包括两类：

(1)在模型切片处理前，对模型进行轻量化建模 Cheah等[1]提出建立基本特征模型库，通过参数化更改基本特征模型的结构参数、空间约束条件、逻辑组合关系来构造多孔结构；Wang等[2]提出蒙皮—桁架的轻质结构来满足模型轻量化和力学特性的要求，从而达到减少模型耗材、提升力学性能的目的；Lyu等[3]提出一种基于Voronoi图的建模方式，利用有限元分析(Finite Element Analysis, FEA)的内部结构优化方法，基于FEA计算模型在外力下的应力图，通过Voronoi图结合应力图生成类蜂窝状内部结构，然而该方法复杂度高，仅适用于部分3D打印工艺。在模型内部建模的方法不但需要大量的布尔运算，而且增加了切片时间，同时切片层上出现大量的岛屿轮廓导致大量的空行程和跳刀，影响成型质量和效率。

(2)模型切片处理后，根据切片轮廓内部扫描路径实现轻量化设计 该方法避免了复杂的轻量化建模方法和后期大量内轮廓的路径规划，提高了成型效率和质量。目前商业3D打印软件(如MakerWare, Replicator等)在模型内部设计网状路径填充，如网状路径，但都没有考虑其力学特性和参数化设计。李维诗等[4]提出利用三组平行间断直线构造蜂窝状扫描路径的方法，但由于该方法采用3个方向间断式扫描，在路径的端点处出现3次重复扫描，使端点处过堆积现象严重，且使切片层面上存在大量空行程和跳刀。Ponnusamy[5]和Gurunathan等[6]提出采用不同的分形曲线对医学生物支架的切片薄层进行填充，通过改变分形曲线的类型和填充密度实现了多孔医学模型制造，该方法的缺陷是当分形曲线的单位步长较大时，将降低相邻路径上的丝材搭接率和模型强度。

蜂窝状结构具有优良的承载和轻量化特性，Zhang等[7]介绍了蜂窝结构产品的设计原则和制造性能(如机械、热和声学性能);Ingrole等[8]进行新拉胀蜂窝体结构的新颖设计和性能改进研究，该结构具有优异的冲击能量吸收性能和独特的机械性能;Hedayati等[9]使用数值和实验方法，提出新的八边形蜂窝结构并研究其机械性能;Aumjaud等[10]根据云图的分布状况在高性能轻质蜂窝结构中插入双剪切搭接接头，可显著增加总质量并改变质量分布。基于面外压力蜂窝结构的机械性能理论研究和有限元实验[11-13],Li等[14-15]研究了金属铝蜂窝轴向压缩下的能量吸收性能，为用作缓冲和碰撞结构的金属蜂窝提供了理论基础。上述文献针对蜂窝结构的设计、机械性能和数值分析方法进行了广泛研究，但尚无基于材料损耗和应力分布驱动的自适应蜂窝打印轨迹生成技术的研究。

本文提出一种参数可控制的自适应蜂窝轨迹生成方法，针对耗材问题和强度问题进行了理论研究和实验验证，实现了基于材料最少、承载最大和应力分布的自适应蜂窝轨迹生成。

1 方法概述

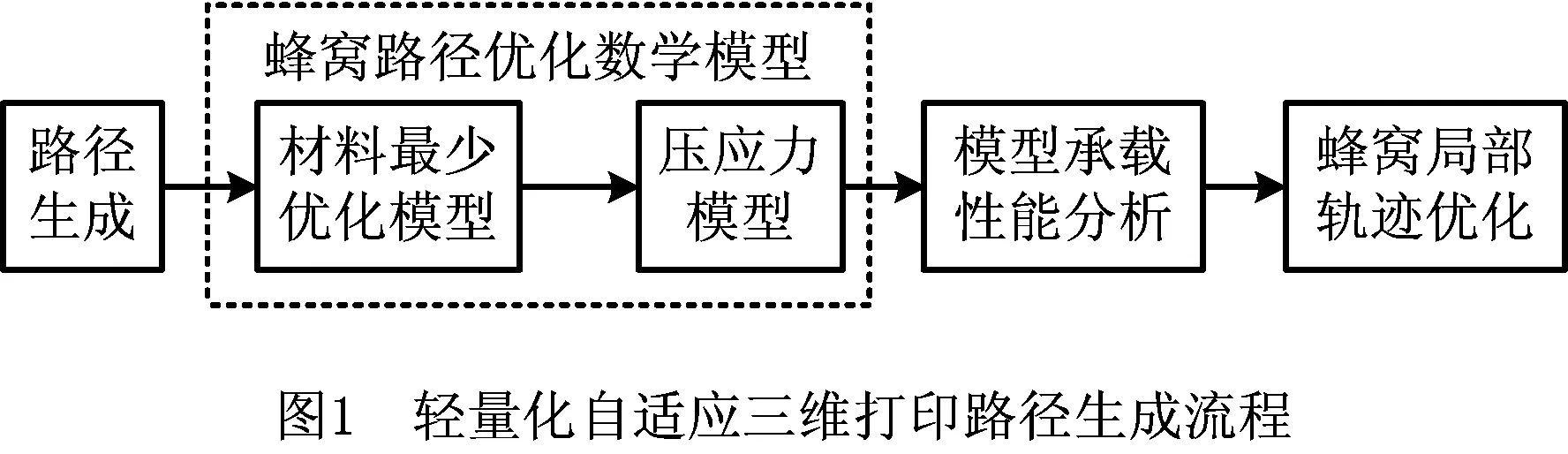
蜂窝轻量化3D打印路径自适应设计包括4部分内容(如图1)：①参数化蜂窝路径生成，包括蜂窝单元的排布、填充和裁剪过程；②蜂窝路径优化数学模型，包括基于材料最少的优化模型和压应力模型的优化模型构建；③使用有限元软件分析蜂窝结构承载性能；④非均布载荷下蜂窝局部轨迹的优化设计，生成满足承载性能的轻量化蜂窝打印轨迹。

2 蜂窝状路径的参数化生成

路径单元类型直接影响模型的力学和轻量化特性，单层或双层壁厚的蜂窝状路径会导致模型承力不均，分形路径会降低模型承载能力。本文首先对类蜂窝路径进行参数化建模。

2.1 蜂窝状路径单元排布设计

现有的3D打印系统采用单双壁的蜂窝状路径，这种方法不能保证模型承力的均匀性。设计的参数可控的等壁厚蜂窝状路径排布方式如图2所示。图中：l表示蜂窝单元的边长，可以通过改变边长调整填充区域蜂窝单元排布的疏密和大小；d表示相邻蜂窝单元的间距，其大小决定了相邻胞元的搭接率，为保证相邻胞元粘连牢固，d必须小于成型的丝材宽度或激光光斑直径；λ表示蜂窝的原始排布单元向内偏置的次数，其大小决定了蜂窝状胞元壁厚的大小。根据不同的力学工况调节3个参数，不仅能够实现胞元参数化设计，还可以优化模型的承载性能。

2.2 蜂窝状路径单元填充算法

为了保证模型蜂窝状路径单元网格能覆盖切片轮廓，且相邻上下切片轮廓的蜂窝状路径单元不发生错位现象，以模型最小包围盒来确定所有切片层单元的初始填充区域(如图3)，模型的填充路径在未经裁剪前，每层的蜂窝状填充完全一致。

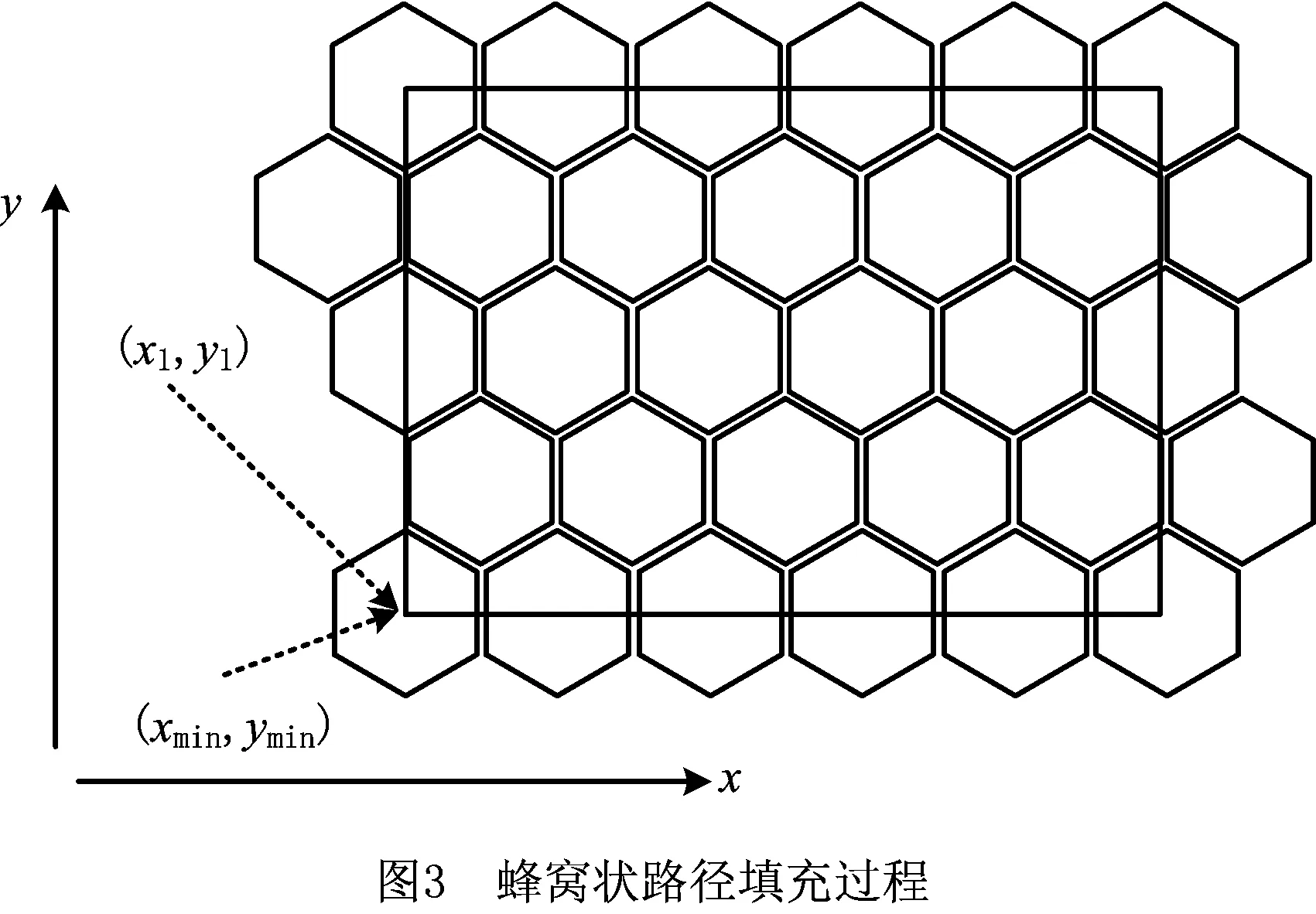
设置蜂窝单元中心坐标(xi,yi)和(xj,yj)；轮廓包围盒的极小值点(xmin,ymin)和极大值点(xmax,ymax)。具体算法步骤如下：

步骤1初始化蜂窝单元的中心坐标(xi,yi)，转步骤2。

步骤3如果新的中心坐标值超过包围盒的极大值坐标，则算法结束。如果中心点的x坐标大于极大值点的x坐标，则转步骤4； 否则，转步骤2。

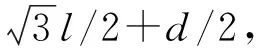
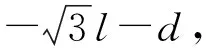
步骤6如果单元中心值的x坐标小于极小值点的x坐标，且y坐标大于极大值点的y坐标，则算法结束。如果x坐标小于极小值点的x坐标，则转步骤4；否则，转步骤5。

2.3 蜂窝状路径单元的分割建模

定义图4a中P0点为单元起始点，并以顺时针顺序保存线段。需要对填充单元(图4a中5个蜂窝状图例)和实际填充区域(图4a中两圆轮廓的相交区域)进行位置关系判断，蜂窝状路径单元与实际填充区域存在4种接触关系(如图4a)：①单元在填充区域外部(H1,H2)则不保存线段；②单元位于填充区域内部(H5)则按顺时针保存其线段；③单元与边界轮廓相交但单元起点在填充区域外部(H3),如图4b所示，则从起始点P0遍历至奇数交点P1，P3时开始保存黑色线段，遍历至偶数交点P2，P4时停止；④单元与边界轮廓相交但单元起点在填充区域内部(H4),如图4c所示，则从起始点P0开始保存加粗线段，遍历至奇数交点P1，P3时停止，遍历至偶数交点P2，P4时再次保存，直至再次奇数点时停止，如此往复循环，直至遍历结束。

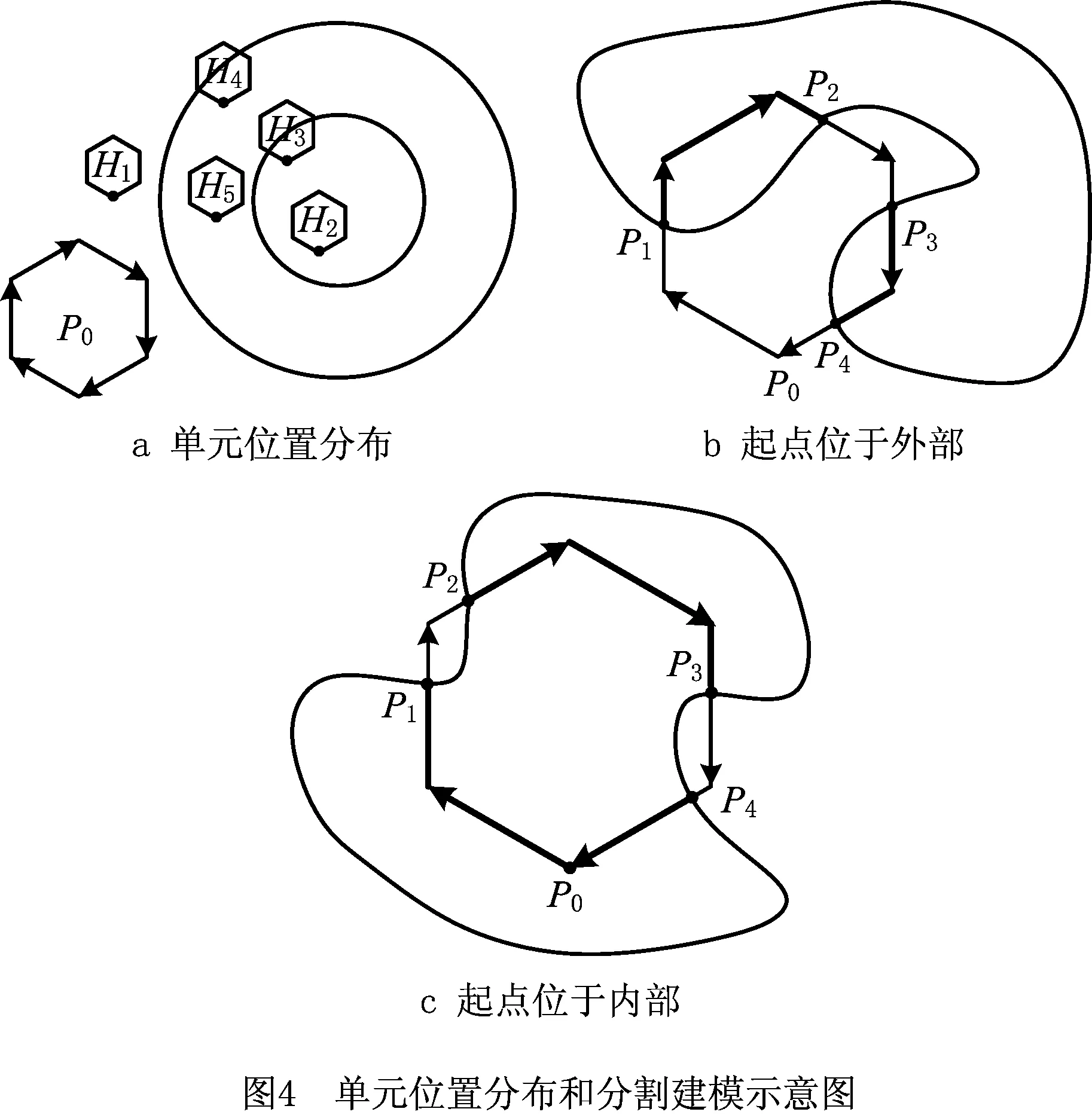
图5a和图5b所示为蜂窝状路径单元在填充区域的完整裁剪结果示意图。

3 自适应蜂窝路径的优化数学模型

3.1 基于材料最少的优化模型

合理的参数设计能保证模型材料最少，依次定义蜂窝单元边长l、单一切片层耗材量Llayer、蜂窝单元面积S、单元填充数目N，为了保证模型的耗材最少，需要对定义参数联合求最优解。首先蜂窝单元边长l不能无限大，若其过长，则单元完全覆盖最大填充区域，失去了填充的意义，因此本文根据模型的最小包围盒限定单元边长的最大极限值

lmax≤Cmin{lx,ly}。

(1)

式中：参数lx和ly分别为模型最小包围盒在x方向和y方向的长度，本文常数C取值0.58。

根据模型内部有效蜂窝状路径总长度决定材料使用量的原则，文中采用单层蜂窝总长度衡量用料量，并且实验中采用商业软件中模型的用料百分比20%作为模型轻量化程度的比例，Ai表示实际填充区域的面积，0.36 mm表示估算丝宽。则每一层上蜂窝有效扫描路径总长

Llayer=0.2×Ai/0.36。

(2)

(3)

建立如下同一切片层上有效扫描路径的总长度和路径参数的关系方程：

(4)

结合式(3)和式(4)可得扫描路径总长度方程为

(5)

蜂窝单元偏置次数λ必须取大于等于0的整数值，且随着边长l的增长，其取值必须满足式(1)，因此结合式(1)、式(2)和式(5)便可以计算得到如表2所示的5组蜂窝轨迹参数。

3.2 自适应压应力轨迹优化模型

在研究蜂窝单元参数化的基础上，更进一步将单元参数和压应力相结合，得到自适应压应力轨迹优化模型，进一步提高生成轻量化模型的承载能力。

基于材料力学基本理论，准静态异面压缩下的典型应力—应变曲线包括3个阶段：

(1)弹性变形阶段 此阶段蜂窝壁相当于弹性杆受正向压缩作用，其应力—应变呈线性关系，力卸载后能够恢复原状，Gibson等[16]和Wang等[17]针对压缩实验的应力做了理论研究。

(2)稳定屈服阶段 随着应力增加，蜂窝壁发生失稳屈服，该过程不断循环发生，导致应力在此阶段呈现不断振荡的形态。

(3)致密化阶段 此阶段蜂窝胞元全部折叠或坏损，蜂窝壁间隙较小，持续压缩会导致应力大幅增加。

本文研究蜂窝的不同边长和厚度参数下的承力能力，即弹性变形阶段的极大值点，该位置对应蜂窝屈服强度，其值可通过下式计算得到：

(6)

式中：Es为蜂窝基体材料的弹性模量；vs为蜂窝材料泊松比；k为蜂窝胞元端面的约束因子；对于正六边形蜂窝l=h，均为蜂窝胞元的边长；θ为相邻蜂窝胞元所夹的锐角；t为蜂窝胞元壁厚。则式(6)中只有t，l是未知量，常量可带入数值简化为常数C，得到

(7)

在蜂窝压缩力学研究中，根据式(7)可知蜂窝屈服强度与t/l比值有关。

4 仿真与计算结果

4.1 实验条件

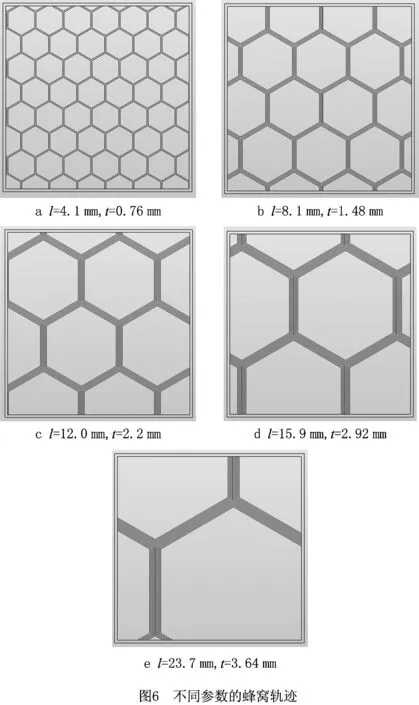
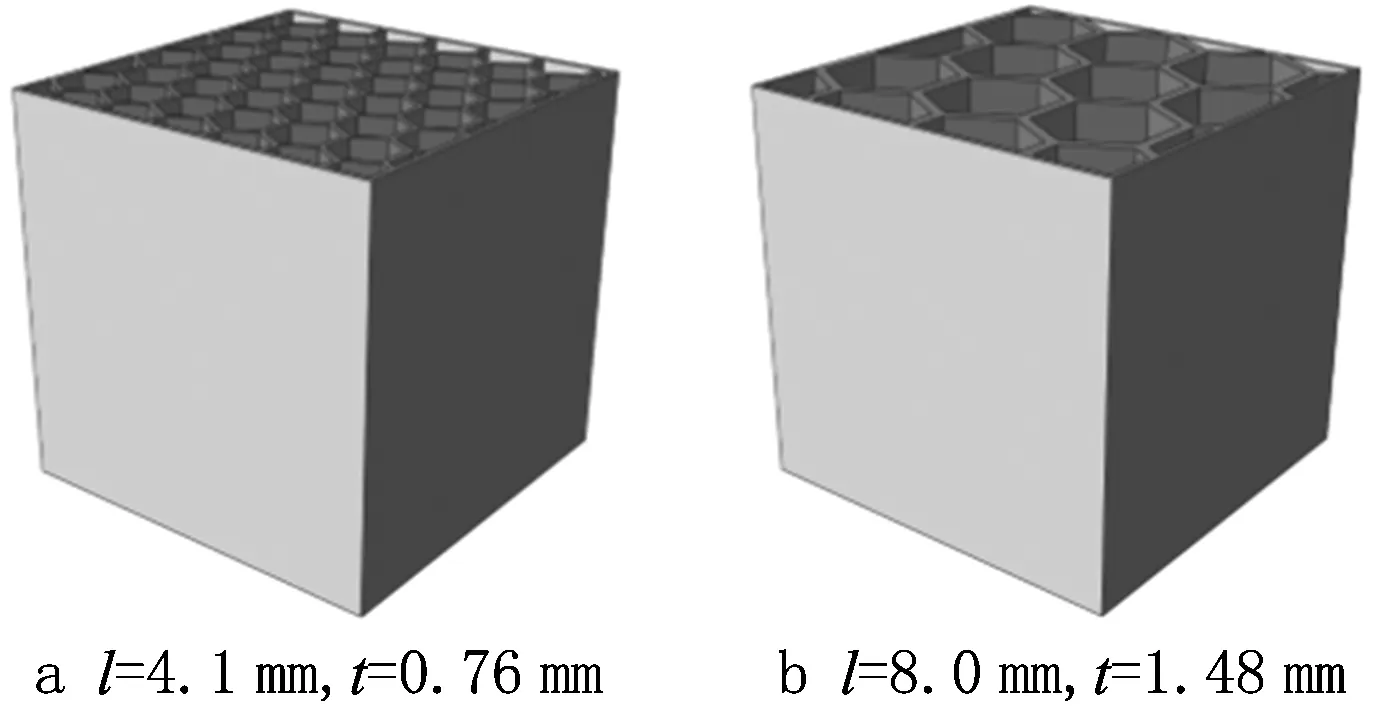
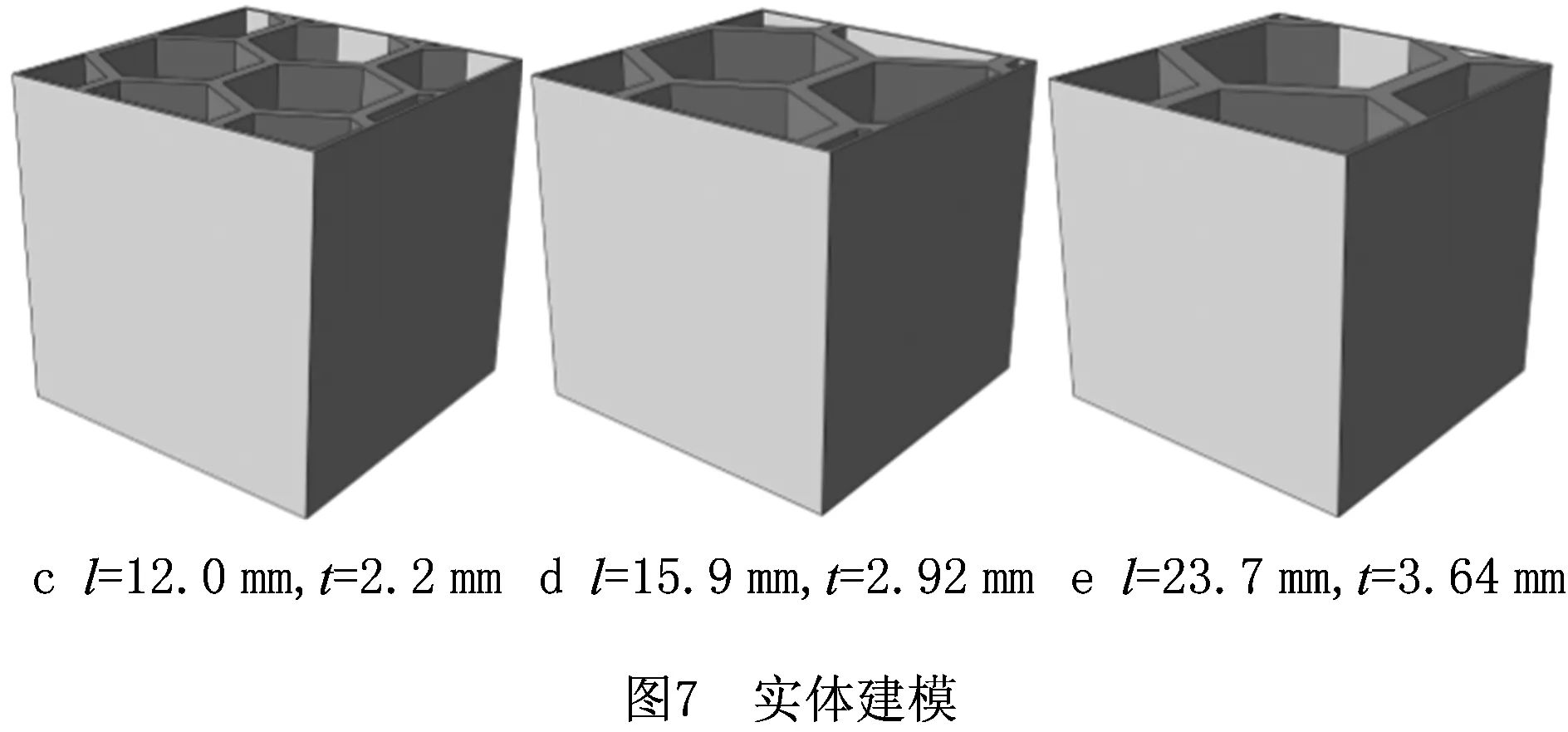
蜂窝作为一种应用广泛的轻量化结构，在实际应用中经常需要承受轴向载荷作用，因此研究蜂窝结构在准静态压缩下的受力响应至关重要，而实际的准静态压缩实验往往耗时费力，且无法获得蜂窝结构的应力分布情况。首先通过蜂窝参数优化设计，使用C++语言在VS2008平台上生成了蜂窝状路径，并且基于OpenGL进行显示，如图6a和图e所示为在单位立方单元生成的参数化轨迹的俯视图，其单元边长l逐渐增大，单元壁厚t逐渐加厚，单元个数N随边长壁厚增大而减少，形成材料不变且参数梯度变化的一组蜂窝轨迹。根据蜂窝结构的边长壁厚参数，使用Solidworks软件在50×50×50 mm立方体中构建有限元实体模型，图7所示为5组不同参数的实体模型，其中每个实体模型的材料(丙烯腈—丁二烯—苯乙烯(ABS))相同。最后，采用Abaqus有限元软件模拟实际压缩的实验环境，对建立的蜂窝结构有限元模型进行数值模拟。

有限元实体模型如图8a所示，所用材料为丙烯腈—丁二烯—苯乙烯，材料参数如表1所示，该结构的参数如表2所示。本文构建立方体模型中的蜂窝结构，使用Abaqus/CAE 6.13-1软件包构建充当实际准静态实验压头和底座夹具的刚体模型。

FEA过程中模型的边界条件如图8a所示，将模型放置在两个刚性板之间，并且两刚性板和模型的切向摩擦系数设为0.2。顶板只保留Z向的位移自由度，底板则约束其所有自由度，通过在上刚性板参考点的Z轴方向施加负向位移边界载荷来模拟实际压头对模型的压缩测试，在保证线弹性阶段的基础上允许顶板在Z方向位移1 mm～2 mm。在保证模型精度和节省时间的前提下，文中使用C3D10的单元类型进行模型的网格划分，网格是具有四面体特征的元素。

4.2 自适应蜂窝结构承载性能验证

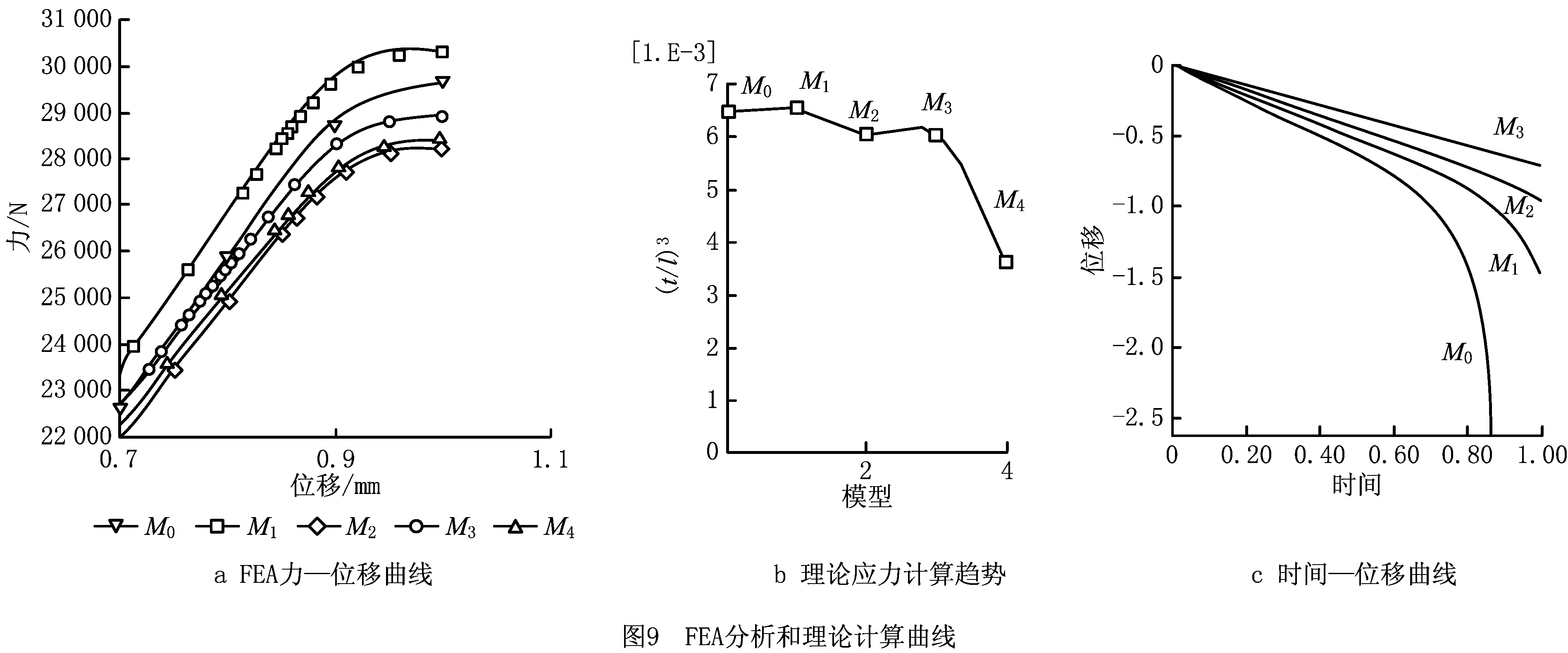
图8b～图8f所示为FEA的应力分布云图，该图采用垂直Z轴平面截取试样云图，更直观地展示了内部云图的分布状况，表示了模型在图9a力—位移曲线线性拐点处的云图分布状况。灰色云图区域表示立方体模型的最早失效区域，其应力明显高于蜂窝结构的极限应力；红色云图区域表示蜂窝结构达到破裂极限。比较图9a所示的5种蜂窝结构试样在线弹性阶段的力—位移曲线可知，l=8.0mm，t=1.48 mm的试样在线性弹性阶段的承载能力最大，其他试样的承载能力略小，且相互间的承载能力不是线性递减关系，而存在细微的波动。由应力理论公式可知，模型在线性弹性阶段的极限应力与单元间距边长的比值(t/l)3成正比关系，表2计算出了(t/l)3的比值，所生成的曲线如图9b所示。比较5种试样可知，参数l=4.1 mm，t=0.76 mm和l=8.0 mm，t=1.48 mm试样的(t/l)3比值近似相等，其他试样的参数比值略小，前两个试样的极限应力略大于其他试样，即前两个试样的承载能力强于其他试样。由此得到结论，l=8.0 mm，t=1.48 mm的试样承载能力最强约为30 kN，l=4.1 mm，t=0.76 mm和l=8.0 mm，t=1.48 mm试样相差不大，其余试样的承载能力呈波动状递减。

4.3 非均布载荷下的蜂窝轨迹生成与性能验证

在4.2节均布载荷研究基础上得出结论，在材料用量不变且模型需要承受较强载荷时，可以直接使用l=8.0 mm，t=1.48 mm试样蜂窝路径单元的边长壁厚参数对模型进行轻量化设计，得到蜂窝轨迹路径。针对非均布载荷作用于模型右下角区域的情况，通过算法生成局部蜂窝单元壁厚增加的轨迹路径(如图10b～图10d)，根据该区域的应力分布状况，自适应地增加模型右下角区域蜂窝及周围相邻单元的壁厚，生成蜂窝单元壁厚从左上角到右下角梯度增加的轨迹，进一步增强了该结构承受非均布载荷的能力。

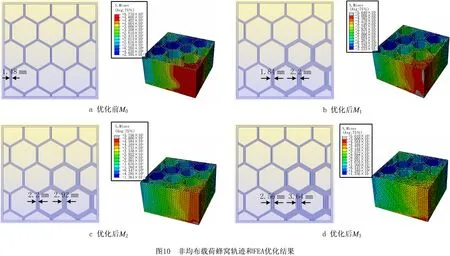
模型优化前后的时间—位移曲线如图9c所示，其中曲线M0表示蜂窝结构优化前，M1～M3表示蜂窝结构局部增加壁厚优化后，曲线M0线性拐点的位移比M1～M3大，蜂窝结构优化后的局部壁厚越大强度越高。根据FEA得到的实验结果如下：均布载荷获得参数构建的轻量化模型在承受非均布载荷时的云图如图10a所示，红色区域为蜂窝结构受非均布载荷优化前的云图分布范围，图10b～图10d是对应力集中区域的蜂窝结构增加壁厚优化后的云图，红色应力集中区域明显比优化前减小，说明随着模型局部应力集中区域的蜂窝壁厚不断增加，该部位承载能力不断增强，应力集中现象不断减弱。模型优化前后的时间—位移曲线如图9c所示，其中曲线M0表示蜂窝结构优化前，M1～M3表示蜂窝结构局部增加壁厚优化后，曲线M0线性拐点的位移比M1～M3更大，蜂窝结构优化后的局部壁厚越大，强度越高。

5 结束语

本文针对3D打印模型的轻量化问题提出面向应力分布的自适应3D打印路径生成技术。首先给定耗材和均布载荷约束，通过将蜂窝单元参数化来构建具有承载能力的轻量化蜂窝轨迹，并使用有限元软件分析轻量化模型的承载能力，获得极限应力下的最优蜂窝单元参数;然后对获得的优化蜂窝结构继续给定非均布载荷约束，增加应力集中区域单元壁厚。该设计解决了耗材浪费、打印效率不高、模型力学性能不足的问题。

根据目前实验发现，模型的力学性能还受到复合载荷的影响，本文只讨论了在单一载荷作用下蜂窝结构的轻量化设计，未来工作将进一步研究增加复合载荷工况下蜂窝打印路径的生成，以及每层蜂窝排布不同的多样化设计，并通过力学实验进一步完善自适应生成过程。