产品差异化下的线上与线下供应链合作广告微分对策

肖 剑，李园园，张旭梅

(1.重庆大学 数学与统计学院，重庆 400044;2.重庆大学 建设管理与房地产学院，重庆 400044;3.重庆大学 经济与工商管理学院，重庆 400044)

0 引言

随着互联网电子商务的蓬勃发展和迅速普及，越来越多的消费者通过网络购买商品，消费市场产生了深刻的变化。传统渠道的制造商在天猫、京东等平台上建立了官方旗舰店，通过网上销售降低渠道成本，从而获得更多市场和利润。制造商建立的电子直销渠道与传统零售渠道产生冲突，由于电子直销渠道的成本相对较低，以实体店为代表的零售商渠道受到电子直销渠道的冲击，导致传统零售商利润下降，随着渠道冲突的加剧，品牌影响力进一步被削弱。为了缓解渠道冲突，防止消费者搭便车，一些制造商选择在电子直销渠道和传统渠道投入差异化产品的战略来实现这一目标。例如 GXG 在电子渠道销售往季旧款服装，零售渠道销售最新款服装；周大福珠宝的网络渠道只推出一些设计简单的专款，适合喜欢在线购物收入不高的年轻群体。同时，制造商和零售商推广产品都依赖于广告，因此渠道间成功的广告策略对实现渠道间差异化战略至关重要。合作广告作为一种成本分配机制广泛存在于供应链中，例如Bennan[1]指出在PC行业，Apple为媒体支付75%的广告费用，而IBM承担零售商50%的广告费用。在存在传统渠道和线上渠道的供应链中，实施线上线下的广告合作策略，即零售商对线上渠道投入广告，制造商对传统渠道进行推广，可以提高品牌知名度，从而增加产品需求并最终提高利润，在产品差异化的背景下实施这样的合作广告策略是有吸引力的。

目前，有关合作广告策略的研究集中在只存在一个制造商和零售商的供应链，制造商通过分对零售商在传统渠道的广告投入，使零售商提高在其传统渠道的广告投入[2-3]。目前已经有相当多的学者对合作广告的问题进行了研究，聂佳佳[4]用微分对策的方法研究了竞争条件下供应链的合作广告问题，得到了制造商对零售商传统渠道广告投入进行补贴的充分条件；陈国鹏等[5]研究了折扣条件下在线零售商二级供应链广告分担模型，并得到了集中决策下系统的广告投入和供应链系统总利润均大于分散决策情况下广告投入和供应链总利润的结论；蔡洪文等[6]分析了零售商处于领导地位时一个供应商和一个零售商的二级供应链合作广告契约，得出合作广告契约能够使零售商主导的供应链协调的结论；Jorgensen等[7]通过研究营销渠道中制造商和零售商的营销策略，发现合作广告计划是实现供应链协调的一种机制，该机制能够实现Pareto改进，提高制造商和零售商的收益；陈远高[8]研究了电子供应链中多渠道协调的问题，提出横向服务机制来实现供应链协调。一些文献进一步研究了动态环境下的合作广告策略，增加了商誉、价格和需求等因素，聂佳佳等[9]研究了需求变化下的合作广告问题，分析了价格敏感因素和需求敏感因素的影响，得出了协调供应链的条件；李昌文等[10]研究了随机条件下过度自信的零售商和理性的零售商的期望利润和实际利润；张建军等[11]用微分对策的方法研究了时间变化条件下的商誉，求出了相应合作广告的微分对策；聂佳佳[12]运用汉密尔—雅可比贝尔曼方程讨论了商誉概率分布下的分担比例，并得到了一定条件下合作博弈的系统总利润总是高于Stackelberg博弈下的系统利润的结论。一些文献进一步探讨了品牌差异化对双渠道供应链的影响，Yan[13]研究了电子直销商通过在双渠道供应链中实施品牌差异化策略来解决渠道间的冲突，得到了产品差异化能够缓解渠道间竞争的结论；张旭梅等[14]利用微分对策的方法讨论了存在品牌差异的双渠道供应链合作，得出相比Stackelberg博弈，集中决策下的系统能够获得更大利润的结论；赵德余等[15]研究了Stackelberg博弈下，产品差异化的变动对企业均衡利润产生的影响；陈远高等[16]探讨了电子直销渠道的接受程度和产品差异化程度对供应链及其成员利润的影响；陈静等[17]通过构建差异化产品横向并购模型，发现当参与并购的供应链均集中决策时对并购方有利，产品差异化程度与并购效应成反比。Jorgensen等[18]使用微分对策研究动态环境下的合作广告问题，讨论了广告合作的长期效果。

综上所述，一些文献考虑了只存在一个制造商和一个零售商的供应链系统中，制造商对零售商在传统渠道广告投入的分担比例问题，一些文献考虑了产品差异化下的供应链设计，少数文献讨论了产品差异化下制造商对零售商投入广告的分担比例，却缺少差异化下制造商和零售商进行线上线下广告合作，并承担相应的广告分担比例的研究，因此本文引入产品差异化下的线上与线下(Online and Offline, OAO)供应链模型，即线下和线上有机融合的双店模式，通过线上线下资源互通、信息互通，将线下消费者引到线上消费，将线上消费者引到线下消费，分析OAO供应链中品牌商誉及品牌间广告竞争对利润的影响。因为制造商和零售商的广告投入不但影响当期需求，而且影响长期需求，广告投入与时间有关，适合用微分对策方法描述，所以本文用微分对策模型讨论合作广告投入和分担比例设计的问题，最终设计一个双向参与的合作契约来实现供应链的协调。

1 问题描述与模型

1.1 问题描述与假设

模型描述：考虑在只存在一个制造商和零售商的供应链系统中，制造商拥有电子直销渠道，并通过电子直销和零售两个渠道进行销售，零售商的线下渠道和制造商的线上渠道分别销售有差异的商品βr和βe，线上和线下产品相互具有可替代性而产生竞争，竞争强度的大小取决于线上和线下渠道产品间的差异化程度。在一开始不存在“双店经营模式”时，制造商对自己电子渠道产品的广告投入为Aee(t)，零售商对传统渠道产品的广告投入为Arr(t)，其中制造商分担部分费用，分担率为θ1；在引入“双店经营模式”后，制造商对零售商产品的宣传投入为Aer(t)，零售商的分担率为θ3，零售商对制造商电子直销渠道产品进行宣传的投入为Are(t)，制造商的分担率为θ2。

模型假设：

假设1假设成本函数为凸函数，与文献[13]类似，假设渠道广告的成本函数为

y∈(r,e)}。

(1)

假设2假设产品商誉Gi(t)的提高是因在相应的渠道进行了广告投入，与文献[14]类似，用Nerlove-Arrow模型描述商誉的变化，得到以下微分方程：

(2)

式中：λ为广告投入对产品商誉的影响，δ为产品商誉随时间的递减效应，λ，δ≥0。

当i=e时有A=Aee+Are，当i=r时有A=Aer+Arr。

1.2 模型建立

产品差异化下，渠道的广告投入会对渠道需求产生影响，因此根据已有文献进一步拓展两种渠道的需求函数，得到电子直销渠道产品需求函数de(t)和传统渠道产品需求函数dr(t)分别为：

dr(t)=α1Gr(t)-β1Ge(t)+χ1Arr(t)+φ1Aer(t)+

σ[Arr(t)+Aer(t)-Aee(t)-Are(t)];

(3)

de(t)=α2Gr(t)+β2Ge(t)+χ2Aee(t)+φ2Are(t)-

σ[Arr(t)+Aer(t)-Aee(t)-Are(t)]。

(4)

式中：α1为传统渠道所售产品βr的商誉Gr(t)对需求的影响因子，β1为线上直销渠道所售产品的商誉Ge(t)对需求的影响因子，χ1为零售商在传统渠道的广告投入Arr(t)对需求的影响因子，φ1为制造商在传统渠道的广告投入Aer(t)对需求的影响因子，且有α1，β1，χ1，φ1>0；α2为传统渠道所售产品βr的商誉Gr(t)对需求的影响因子，β2为线上直销渠道所售产品的商誉Ge(t)对需求的影响因子，χ2为制造商对直销渠道的广告投入Aee(t)对需求的影响因子，φ2为零售商对直销渠道的广告投入Are(t)对需求的影响因子，且有α2,β2,χ2,φ2>0。对于传统渠道产品βr和直销渠道产品βe，两者之间的差异越大，替代性越低，相应地，两种产品之间的广告差Arr(t)+Aer(t)-Aee(t)-Are(t)对产品需求的影响也越小，用σ表示以上关系，即σ表示线上渠道产品和线下渠道产品间的差异，σ越大渠道间产品的差异越小，相应的竞争越激烈。文中线上线下产品的差异化主要体现在产品型号、价格、工艺等的影响，并用σ衡量其综合影响。当产品的差异较大时，产品的替代性较小，竞争性也就变小，从而形成非价格形式的竞争优势。

假设制造商和零售商有相同的贴现率ρ；制造商传统渠道产品的边际利润为η1，直销渠道产品的边际利润为η2，零售商的边际利润为η3。一定时期内，企业的边际利润可视为常量，根据以上假设可以得到制造商和零售商的利润函数分别为：

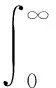
(5)

(6)

式中：θ1为制造商承担零售商对线下渠道产品广告费用的分担比例；θ2为制造商承担零售商对线上渠道产品广告费用的分担比例；θ3为零售商承担制造商对线下渠道产品广告费用的分担比例。

上述模型中出现的参数为常数，在任意时间段内制造商和零售商之间制定的博弈策略视为静态策略，在此基础上达到的均衡状态为静态均衡，因此下文表述中将省略时间单位t。

2 模型分析及主要结论

2.1 集中控制下的决策模型

集中控制决策下，制造商和零售商组成一个供应链系统，双方的共同目标是确定各自的最优广告投入，以使供应链系统实现最大利润。用上标c表示制造商和零售商集中控制决策下的最优广告投入。

集中控制决策下，系统利润函数表示为

(7)

其最优利润函数Ve+r(Gr，Ge)必须满足如下汉密尔顿—雅克比—贝尔曼(Hamilton-Jacobi-Bellman，HJB)方程：

β1Ge+χ1Arr+φ1Aer+σ(Arr+Aer-Aee-Are)]+

η2[α2Gr+β2Ge+χ2Aee+φ2Are-σ(Arr+Aer-

(8)

得到式(8)右端关于Aee，Arr，Aer，Are的一阶偏导条件，联立方程求解得

(9)

设Ve+r(Gr，Ge)=C1Gr+C2Ge+C3,将式(9)带入方程(8)得

ρ(C1Gr+C2Ge+C3)={[(η1+η3)α1+η2α2-

C1δ]Gr+[η2β2-(η1+η3)β1-C2δ]Ge-

χ1+σ(η1+η3-η2)]Arr+

[(η1+η3)φ1+σ(η1+η3-η2)]Aer+

[η2χ2-σ(η1+η3-η2)]Aee+

[η2φ2-σ(η1+η3-η2)]Are}。

上式等号右端除前两项外均为与Gr，Ge无关的常数，因此比较上式等号两端的参数可以得到：

(10)

将式(10)代入式(9)得到定理1。

定理1在供应链系统集中控制决策情形下，供应链双方的最优广告策略分别为：

根据定理1，通过分析供应链成员最优决策和产品差异化的关系，可以得到推论1和推论2。

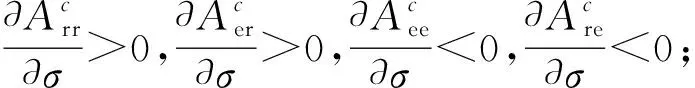
推论1表明，在集中控制决策下，若制造商和零售商在传统渠道的边际利润之和大于制造商在在线渠道的边际利润，则产品差异化值σ变大，制造商和零售商会增加边际利润较高渠道的广告投入，这意味着广告投入会从边际利润低的渠道向边际利润高的渠道转移。

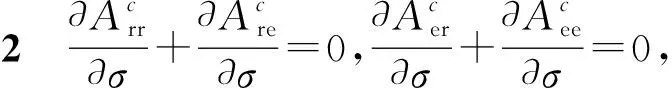
(η1+η3)χ1+(η1+η3)φ1+2λ

推论2表明，在集中控制决策下，随着产品差异化值σ的变化，零售商和制造商在传统渠道和电子渠道广告投入的变化率之和为零，意味着产品的差异化变化不影响制造商和零售商的广告投入和广告总投入，仅影响在传统渠道和电子直销渠道广告投入的分配。

2.2 基于Stackelberg博弈的微分对策模型

假设博弈中的主导者是制造商，确定其最优广告投入和分担比例，在此基础上确定零售商的最优广告投入和分担比例，且最优利润函数Vr(Gr，Ge)应满足以下HJB方程：

φ1Aer+σ(Arr+Aer-Aee-Are)]-

(11)

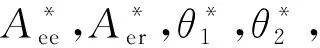
φ1Aer+σ(Arr+Aer-Aee-Are)]+η2

[α2Gr+β2Ge+χ2Aee+φ2Are-σ(Arr+Aer-

(12)

将得到的零售商的反应函数代入式(12)，可得ρVe(Gr，Ge)关于Aee，Aer的二阶导函数为-1<0，求解其对Aee，Aer的一阶导函数并等于零，得：

(13)

设Vr(Gr，Ge)=M1Gr+M2Ge+M3,Ve(Gr，Ge)=N1Gr+N2Ge+N3,将这两个表达式分别带入各自对应的HJB方程得到：

N1δ)Gr-(η1β1-η2β2+N2δ)Ge+

η1[χ1Arr+φ1Aer+σ(Arr+Aer-Aee-Are)]+

η2[χ2Aee+φ2Are-σ(Arr+Aer-Aee-Are)]-

N1[λ(Arr+Aer)]+N2[λ(Aee+Are)]}。

由结果可知Arr，Aer，Aee，Are为与Gr，Ge无关的参数，通过比较上式两端的系数可以得到零售商和制造商最优利润函数的参数值为：

令式(12)关于θ1，θ2的一阶导数为零，得：

(14)

(15)

代入得Arr，Aer，Aee，Are中得到定理2。

定理2在Stackelberg博弈下，制造商和零售商的最优广告投入及分担比例为：

根据推论3得到结论：Stackelberg博弈下，对于制造商为零售商进行线上宣传而产生的费用，零售商的最优策略为不分担。

对定理2做进一步分析，可以得到推论4。

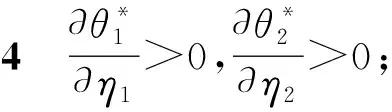
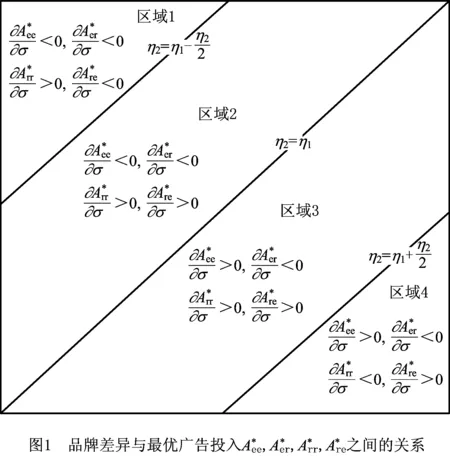
推论5表明，制造商和零售商的最优广告策略与产品差异化之间的关系，很大程度上取决于制造商和零售商在不同渠道边际利润的相对大小。

消费者的购买习惯和品牌定位等诸多因素会对产品的差异化产生影响，上文得到的结论有助于供应链的制造商和零售商根据产品间的差异程度以及制造商和零售商在不同渠道相对利润水平的变化情况实施不同的合作广告策略。

3 双向参与的广告费用分担合同设计

因为集中控制决策下系统的利润水平大于Stackelberg博弈下的利润水平，所以可以通过设计一个协调机制使分散决策下的制造商和零售商采用集中控制下的最优广告策略进行渠道的广告投放，从而提高系统总体收益。为了实现上述目标，引入制造商和零售商双向参与的广告费用分担合同来协调供应链关系。

(16)

(17)

定理3在由一个制造商和零售商组成的供应链系统中，存在一个费用分担合同使供应链达到协调状态，从而使供应链成员都能接受集中控制下的广告决策，并使制造商和零售商的利润都实现Pareto改进。

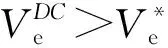
(18)

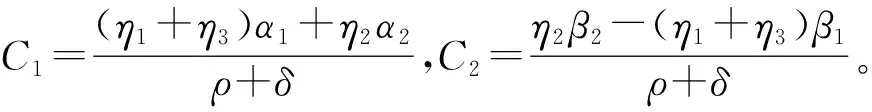
4 算例分析

下面通过算例直观分析产品差异化对制造商和零售商最优广告投入和分担比例的影响。考虑到人民银行确定的商业银行中长期贷款的利率为4.9%，在此取ρ=0.05；考虑广告投入对需求的影响较大，取χ和φ大于α和β；令μ>0，以确保成本函数正凸函数的性质，λ为广告投入对产品商誉的影响，δ为产品商誉随时间的递减效应，令λ>0,δ>0。因此，参数取值如下：ρ=0.05，α1=0.25，μ=0.5，β1=0.05，λ=0.3，δ=0.5，χ1=0.8，φ1=0.6，α2=0.05，β2=0.25，χ2=0.7，φ2=0.8，η1=0.4，η2=0.8，η3=0.3，μ=0.5。

4.1 集中决策下边际利润水平和产品差异化对广告投入的影响

通过改变η2和σ的取值，研究集中决策下供应链成员边际利润水平和产品差异化程度对集中决策下最优广告投入的影响，结果如图2所示。

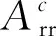
4.2 Stackelberg博弈下广告投入与边际利润及产品差异化间的关系

为了研究Stackelberg博弈下，供应链双方的最优广告投入与不同渠道的边际利润和产品差异化之间的关系，将η2和σ作为变量进行分析，得到如图3所示的结果。

从图3b和图3c可见，随着电子直销渠道边际利润的提高，制造商和零售商都会加大电子直销渠道的广告投入；从图3a和图3d可见，当渠道间的竞争强度较低时，随着竞争强度的提高，为了能够赢得更多的市场份额，零售商会加大传统渠道的广告投入，但是当电子直销渠道的边际利润率增大到一定程度时，零售商会减小传统渠道的广告投入，这是由于制造商将注意力转移到了边际利润更大的电子直销渠道上，减小了传统渠道的分担比例，当分担比例减小到一定程度时，零售商就会减小其对传统渠道的广告投入；从图3d得到了与推论4和推论5一致的结果：①随着竞争程度的增强，制造商会减少传统渠道的广告投入，甚至为零;②电子直销渠道利润率较高且竞争不是很激烈时，制造商仍然会保持传统渠道的投入。这是为了培养线下品牌，通过广告提升品牌价值来提高传统渠道的边际利润，从长远来看，在电子直销渠道和线下渠道竞争不是很激烈的情况下，制造商应保持对传统渠道的广告投入。

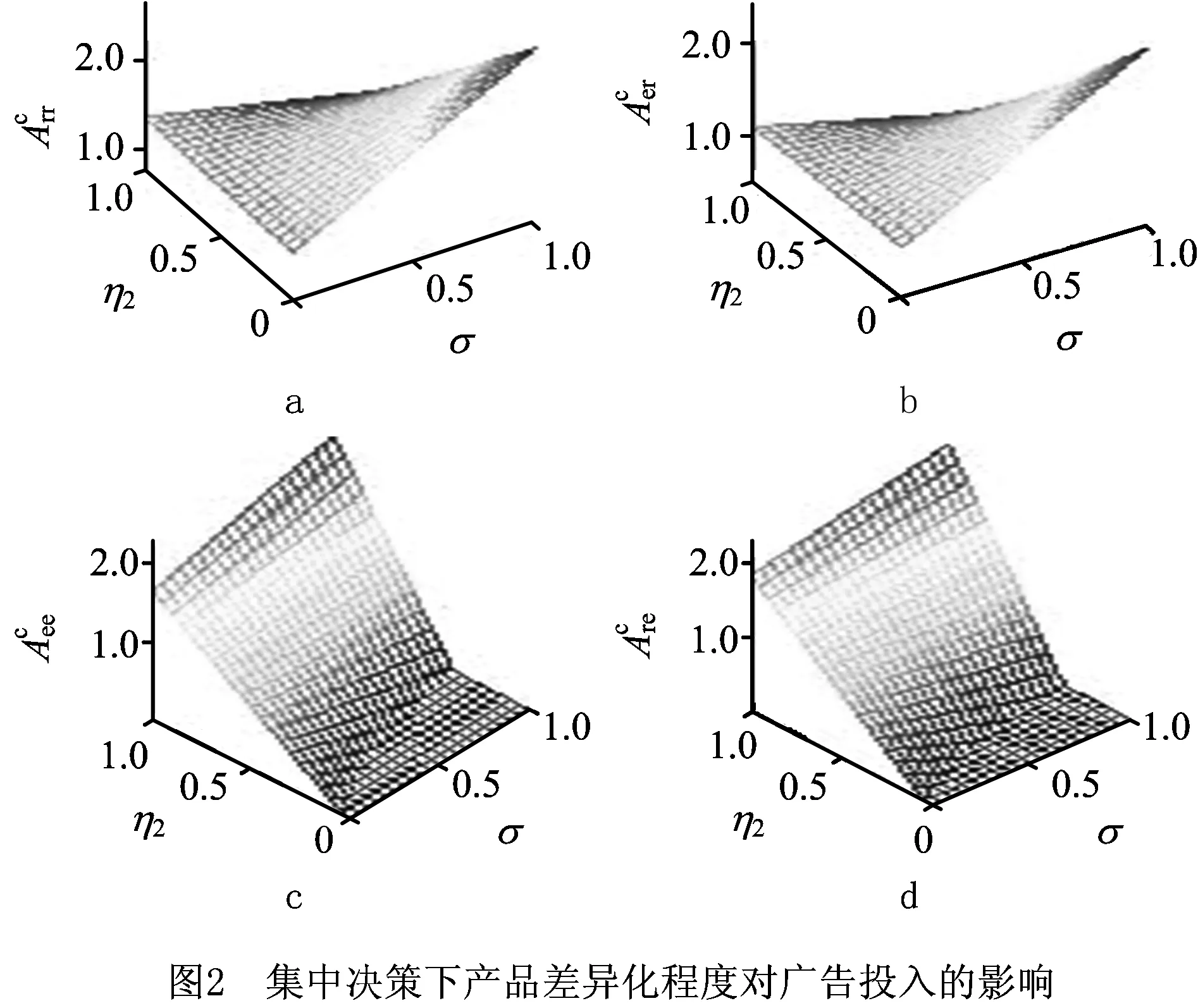
4.3 Stackelberg博弈下边际利润和产品差异程度对分担比例的影响

为了研究Stackelberg博弈下，制造商和零售商不同渠道的边际利润和产品差异程度对最优分担比例的影响，通过改变η3和σ的取值得到如图4所示的结果。

从图4a和图4b可见，当传统渠道边际利润率较低时，随着产品差异化程度的提高，制造商会提高对电子直销渠道和传统渠道广告投入的分担比例;当传统渠道边际利润率较大时，随着产品差异化程度的降低，制造商会减小对零售商在电子直销和在传统渠道广告投入的分担比例。另外，当产品差异化程度较低时，制造商对传统渠道广告投入的分担比例随零售商在传统渠道边际利润的增大而减小，对零售商在电子直销渠道的广告投入的分担比例随着零售商传统渠道边际利润的增大而增大。这与推论4得到的结论一致。

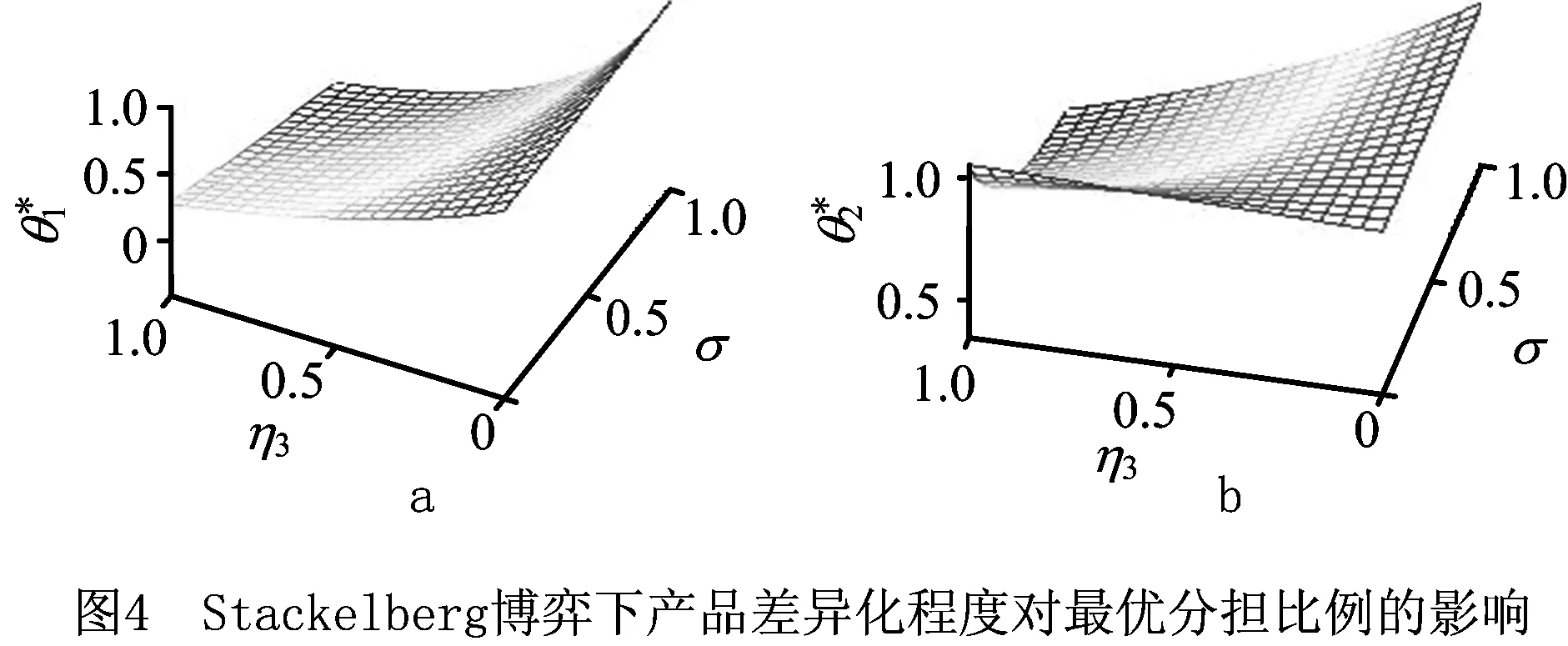
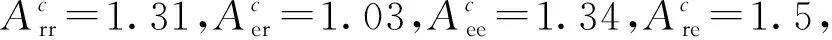
只要θ1，θ2，θ3满足以上不等式，就可以使供应链达到协调。在本算例中，当分担比例为θ1=0.5，θ2=0.5，θ3=0.4时，可以发现分担比例在该集合内能够实现供应链协调。类似地，使供应链协调的分担比例组合可以通过以上方法确定。通过比较集中决策下的系统利润和Stackleberg博弈下供应链的系统利润，可得集中决策下供应链的系统利润比分散决策时增加了29.2%。因此，在存在产品差异化的双渠道供应链中，制造商和零售商通过合同的方式进行集中决策下的合作广告策略，有助于提高供应链的利润水平。

5 结束语

本文主要对产品差异化下OAO供应链制造商和零售商的合作广告问题进行研究，用微分对策的方法得出集中决策及Stackelberg博弈下制造商和零售商的最优合作广告策略，在此基础上分析广告分担比例和产品差异化程度对广告决策的影响。通过研究发现：①在集中决策下，随着OAO同类产品差异化的减小，制造商和零售商都会加大对边际利润高的渠道的广告投入，该结论也在文献[14]得到验证；②在分散决策下，产品间的差异越大，制造商增大承担零售商对OAO渠道产品广告投入的意愿越强烈，因此产品差异化能促进制造商与零售商的广告合作；③当产品差异化程度较低时，制造商对传统渠道广告投入的分担比例随零售商在传统渠道边际利润的增大而减小。最后，本文设计了一个广告分担合同，以实现供应链协调并提高供应链双方的利润水平。文中同时提供了分担比例的确定方法，可以为在OAO供应链实施产品差异化下的广告合作提供参考。

本文研究中的商誉是确定的，没有考虑企业广告投入效果带有不确定性的随机商誉，另外本文也没有涉及零售商竞争环境下的合作广告问题，未来可以从以下几个方面对本文研究进行拓展：①引入随机微分对策理论讨论随机合作广告模型；②考虑商誉的不确定性对广告投入的影响；③将单个制造商单个零售商的动态合作广告拓展到多个零售商的情形。