基于动态优选元胞遗传模糊聚类的使用可靠性区域粒度确定方法
2018-09-08揭丽琳刘卫东滕沙沙
揭丽琳,刘卫东+,滕沙沙,孙 政
(1.南昌大学 机电工程学院,江西 南昌 330031; 2.南昌航空大学 经济管理学院,江西 南昌 330063)
0 引言
可靠性已经成为衡量空调质量属性的核心指标和企业获得产品竞争优势的重要因素。不同地理区域的自然环境、用户经济状况和生活习惯等因素的差异,使产品所处的工作条件和使用时间不一致,导致其实际使用可靠性存在较大程度的区域差异[1-2]。从影响产品使用可靠性因素的角度,按照所处地理区域对其使用可靠性进行科学合理地分类,能够使其在同类区域的相似性和不同区域的差异性尽可能大,以准确预测不同区域产品使用的可靠性水平,这不仅有助于提升产品的设计、制造和成本管理水平,还是实现产品个性化营销策略、区域化保修管理、差异化延保服务等任务的基础。
近年关于空调可靠性的研究逐渐增多,但只有少量研究成果涉及分析空调使用可靠性的区域粒度划分。目前已从空调系统和零部件的失效分析[3-6]、系统可靠性评估[1,7-8]、系统可靠性分析预测与分配的模型构建[9]以及系统可靠性影响因素分析[10-13]等方面对空调可靠性进行了研究。关于空调使用可靠性影响因素分析,目前主要采用实验等手段研究影响空调使用可靠性的相关因素和条件,并取得了一定的成果。例如,Yau等[10]从制冷与制热负荷、电力消耗和室外设计条件3方面分析了马来西亚热带地区气候变化对空调系统的性能和可靠性的影响;Li等[11-12]分别对夏热冬冷地区的太阳能空调、热带地区的分体式空调系统进行实验,通过数值仿真分析了气候变化对空调制冷制热性能的影响;Nishida等[13]对于应用在对温度有严格要求的数据中心等场合的空调系统,研究了从电源失效到恢复供电的间隙对其可靠性的影响。而分析可靠性影响因素与区域差异的关联性并将其应用于相关产品使用可靠性区域粒度划分的研究极其有限,仅有刘卫东等[1]分析了具有区域差异性的温湿度气候条件对空调可靠性的影响,并应用于亚热带季风气候区省会城市的聚类。Jie等[2]在系统研究影响空调使用可靠性的工作环境因素和用户使用习惯因素区域差异性的基础上,构建了区域聚类综合评价模型,通过加权的Ward法求解实现空调使用可靠性的区域分类。然而该研究更多的是关注空调可靠性影响因素分析的全面性及各影响因素的量化,缺乏专门针对使用可靠性区域粒度确定方法的深入分析和探讨,而且信息技术的发展和各种先进量测设备的应用,使得数据采集和存储更加便捷,由此产生大量实时动态且结构复杂的高维数据集,例如空调区域样本的聚类特征多达百维以上,因此采用传统聚类方法无法有效解决使用可靠性区域的粒度划分问题。另外,在实际区域分类问题中,地域样本之间往往缺乏明确的界限,采用传统聚类算法将每个待分类区域严格划分到某个类中也存在一定的不合理性。为此,马军杰等[14]应用模糊C-均值(Fuzzy C-Means, FCM)聚类方法对中国31个省市专利产出数据进行区域划分,其采用的模糊划分矩阵既具有一定的明晰性,又保持了样本数据在空间分布的模糊性,从而提高分类的准确性,但其存在对初始聚类中心敏感和易陷入局部极值等不足,直接影响了区域分类的有效性和合理性。
在解决模糊聚类问题时,国际上涌现出了许多经典的智能聚类算法,如将遗传算法(Genetic Algorithm, GA)和粒子群优化(Particle Swarm Optimization, PSO)算法等优化技术引入聚类分析领域,其中典型算法有遗传模糊聚类算法(Fuzzy Clustering Algorithm based on Genetic Algorithm, GA-FCM)[15]、粒子群优化模糊聚类(Particle Swarm Optimization for Fuzzy Clustering, PSO-FCM)算法[16]等。近年来,Ye等[17]提出一种改进的基于量子遗传算法的模糊C-均值聚类算法(Fuzzy C-Means clustering algorithm based on Improved Quantum Genetic Algorithm, IQGA-FCM),并通过仿真比较验证了所设计的算法性能最优。Ding等[18]将该技术与改进的GA结合,提出一种基于遗传算法的核模糊C-均值聚类算法(Kernel-based Fuzzy C-Means clustering algorithm based on Genetic Algorithm, GAKFCM),并与其他算法的仿真结果比较,证明了GAKFCM算法的有效性。Wikaisuksakul[19]将改进的非支配排序遗传算法(Non-dominated Sorting Genetic AlgorithmⅡ, NSGA-Ⅱ)与FCM有效结合起来,提出一种多目标遗传模糊聚类算法FCM-NSGA(non-dominated sorting genetic algorithm with fuzzy C-means for automatic data clustering), 通过在基准测试数据集上的算法比较,表明所提方法非常有效。Zhang等[20]提出一种基于GA,PSO和FCM的混合聚类算法GCQPSO-FCM(chaotic particle swarm and fuzzy C-mean clustering based on genetic algorithm),并通过仿真比较,验证了该混合算法的性能比单一算法更优。Chen等[21]提出一种改进的粒子群与FCM的混合聚类算法(Hybrid clustering algorithm based on Particle Swarm Optimization and Fuzzy C-Means, HPSOFCM),并对所提算法的性能进行了分析。Li等[22]提出一种基于混沌粒子群优化的模糊聚类算法(Chaotic Particle Swarm optimization based Fuzzy Clustering algorithm, CPSFC),仿真结果显示,该方法比FCM和PSO-FCM具有更好的聚类性能。Izakian等[23]将模糊粒子群优化(Fuzzy PSO, FPSO)引入FCM中,形成一种混合聚类算法FCM-FPSO,实验数据显示,该方法找到的解要比FCM和FPSO更好一些。SilvaFilho等[24]在文献[23]的基础上,运用改进的自适应粒子群优化算法(Improved self-adaptive Particles Swarm Optimization, IDPSO)替换FPSO,提出一种改进的混合聚类算法FCM-IDPSO,并通过仿真比较,表明所设计的FCM-IDPSO算法在聚类精度和收敛时间方面具有比HPSOFCM,CPSFC,FCM-FPSO更优越的性能。
尽管上述模糊聚类方法在解决数据聚类问题上取得了不同的效果,但是对于解决高维度复杂数据聚类问题,其聚类性能依然不尽人意,仍未克服GA或PSO算法陷入局部最优的缺陷,而且增大了算法的复杂度,使得耗时过长,极大限制了其工程应用范围。Alba等提出的元胞遗传算法(Cellular Genetic Algorithm, CGA)[25]具有规则的邻域结构,在一定程度上降低了选择压力和优势基因的扩散速度,能够有效保持种群多样性,在解决各种复杂优化问题时的全局搜索能力比其他算法明显提高。
因此,针对目前存在的问题,本文着眼于产品使用可靠性影响因素分析的全面性和聚类方法的有效性,结合CGA良好的多样性、全局搜索能力和FCM良好的局部搜索能力,在CGA算法中引入信息熵理论[26]度量多样性,并采用动态交叉和基于熵的两阶段变异算子,以及黄金分割优选策略,提出一种动态优选元胞遗传模糊聚类算法IDCGAFCM(improved dynamic optimal-selection cellular genetic algorithm for fuzzy clustering),以达到高效求出产品使用可靠性区域粒度划分问题最优聚类结果的目的。
1 使用可靠性区域聚类模型
1.1 使用可靠性影响因素分析
空调的可靠性是其具有的制冷、制热、除湿和通风等各项功能可靠性的综合。空调使用过程中因工作负荷、自然环境因素以及安装等服务质量因素的影响而产生损耗,其可靠性随使用时间的增长逐渐衰减;在非使用状态下,自然环境因素的反复作用也使空调产生耗损,进而影响空调的可靠性。而空调是否开机使用,既受自然环境因素影响,也取决于用户的使用习惯。因此,可将影响空调可靠性的因素归纳为工作环境影响因素和用户使用习惯影响因素两大类。
一方面,空调及其零部件或元器件在温度、湿度、日照、降水量、粉尘颗粒物和二氧化硫等自然环境因素的循环作用下,出现疲劳、老化、耗损或腐蚀,进而影响空调的使用可靠性;另一方面,空调的使用情况或工作时间也与温度、湿度、日照、降水量和风速等自然环境因素密切相关。由于粉尘颗粒和二氧化硫的数据不完备,在此忽略其对使用可靠性的影响。
空调使用时间主要受用户使用习惯的影响,而影响用户使用习惯的主要因素有用户所处地理区域的自然环境、经济条件和政府补贴等。政府补贴具有促进居民消费的作用,但由于持续时间有限,在此忽略其对用户使用习惯的影响;经济条件可通过社会消费品零售总额增长率、平均消费倾向两个因素反映。综合以上分析,建立如图1所示的产品使用可靠性区域聚类的物理模型。
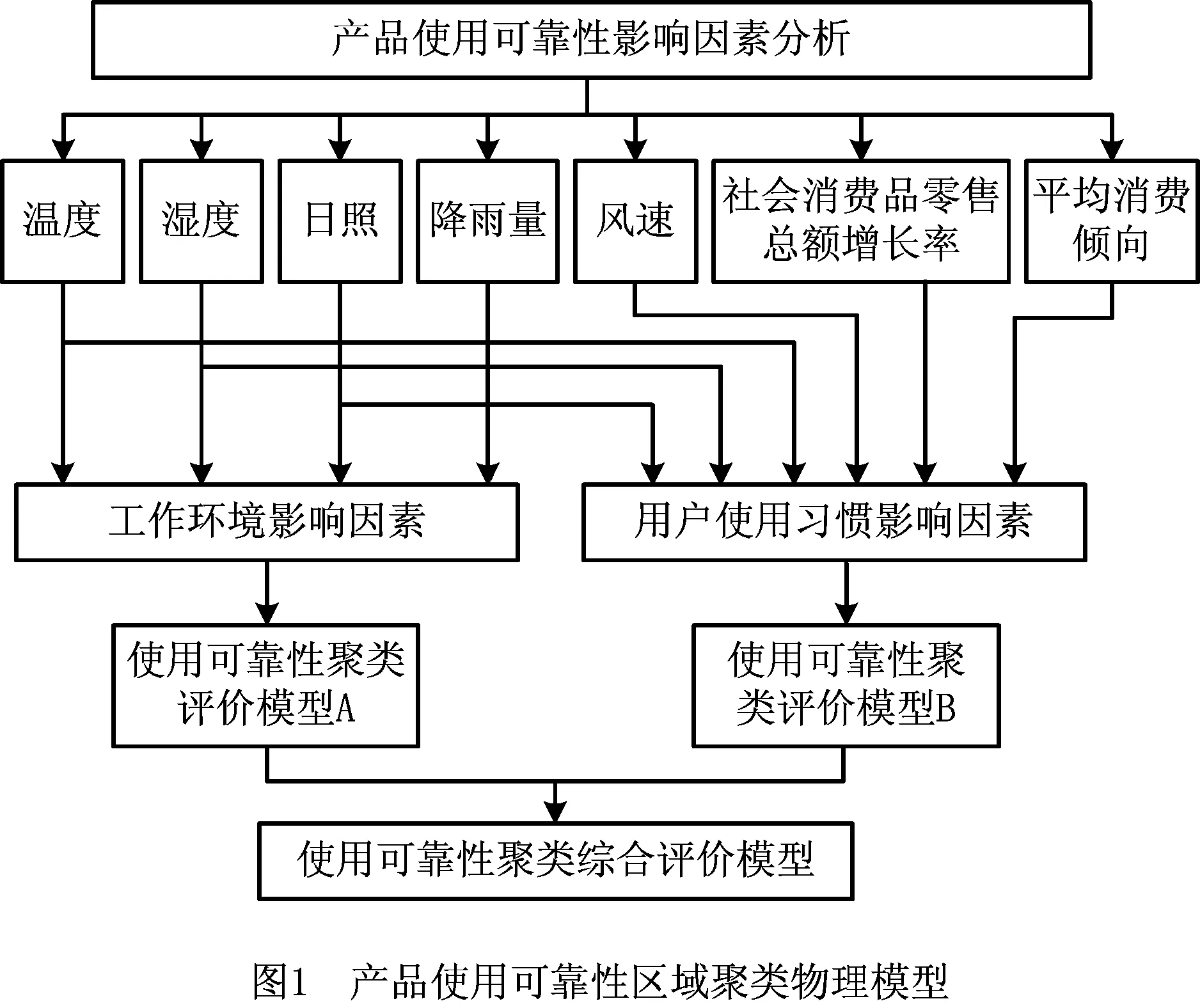
该物理模型综合考虑工作环境和用户使用习惯两类因素的影响,将使用可靠性区域粒度划分问题分解为基于工作环境影响因素的使用可靠性区域聚类和基于用户使用习惯影响因素的使用可靠性区域聚类两个子问题,最后通过综合两个子问题的解,即二次聚类,获得最终的使用可靠性最优区域聚类结果。
因此,上述模型需要同时考虑两个聚类设计目标:①使用可靠性在工作环境影响因素上具有一致性的区域分布;②使用可靠性在用户使用习惯影响因素上具有一致性的区域分布。这两个目标一方面使同一类型区域的产品使用可靠性基于工作环境因素具有最大的相似性,另一方面使同一类型区域的产品使用可靠性基于用户使用习惯因素具有最大的相似性。因此,产品使用可靠性区域粒度划分是多组高维特征样本的复杂数据聚类问题。
1.2 数据结构描述与聚类目标函数的建立
面板数据具有能容纳多指标、综合考虑指标动态发展特征等优良的性质,为充分利用使用可靠性影响因素的动态和局部变化属性信息,克服以往方法中数据不足和丢失问题,构造基于工作环境影响因素和用户使用习惯影响因素的面板数据集模型,分别表示为:
Α={Οks(t)|k=1,2,…,n;s=1,2,…,m;
t=1,2,…,T};
(1)
Β={Ωks′(t)|k=1,2,…,n;s′=1,2,…,m′;
t=1,2,…,T}。
(2)
式中:Οks(t)表示使用可靠性基于工作环境影响因素的第k个聚类样本的第s个特征在t时刻的数值;Ωks′(t)表示使用可靠性基于用户使用习惯影响因素的第k个聚类样本的第s′个特征在t时刻的数值。为了直观表示模型Α,Β的特征,下面给出其在t时刻的数据结构。
在t时刻,产品使用可靠性基于工作环境因素的聚类样本k的特征矩阵Οk(t)及基于用户使用习惯因素的聚类样本k的特征矩阵Ωk(t)分别为:
Οk(t)=[ΓkHkSkRk];
(3)
式中:Γk,Hk,Sk,Rk分别表示其第t年各月的平均温度、湿度、日照、降水量特征矢量,
Γk={tkj|j=1,2,…,12},
Hk={hkj|j=1,2,…,12},
Sk={skj|j=1,2,…,12},
Rk={rkj|j=1,2,…,12};

Vk={vkj|j=1,2,…,4},
Gk={gkj|j=1,2,…,4},
Ck={ckj|j=1,2,…,4}。
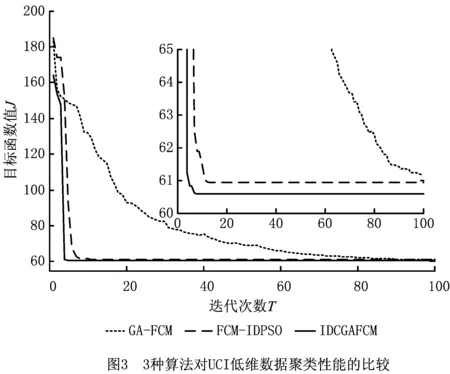
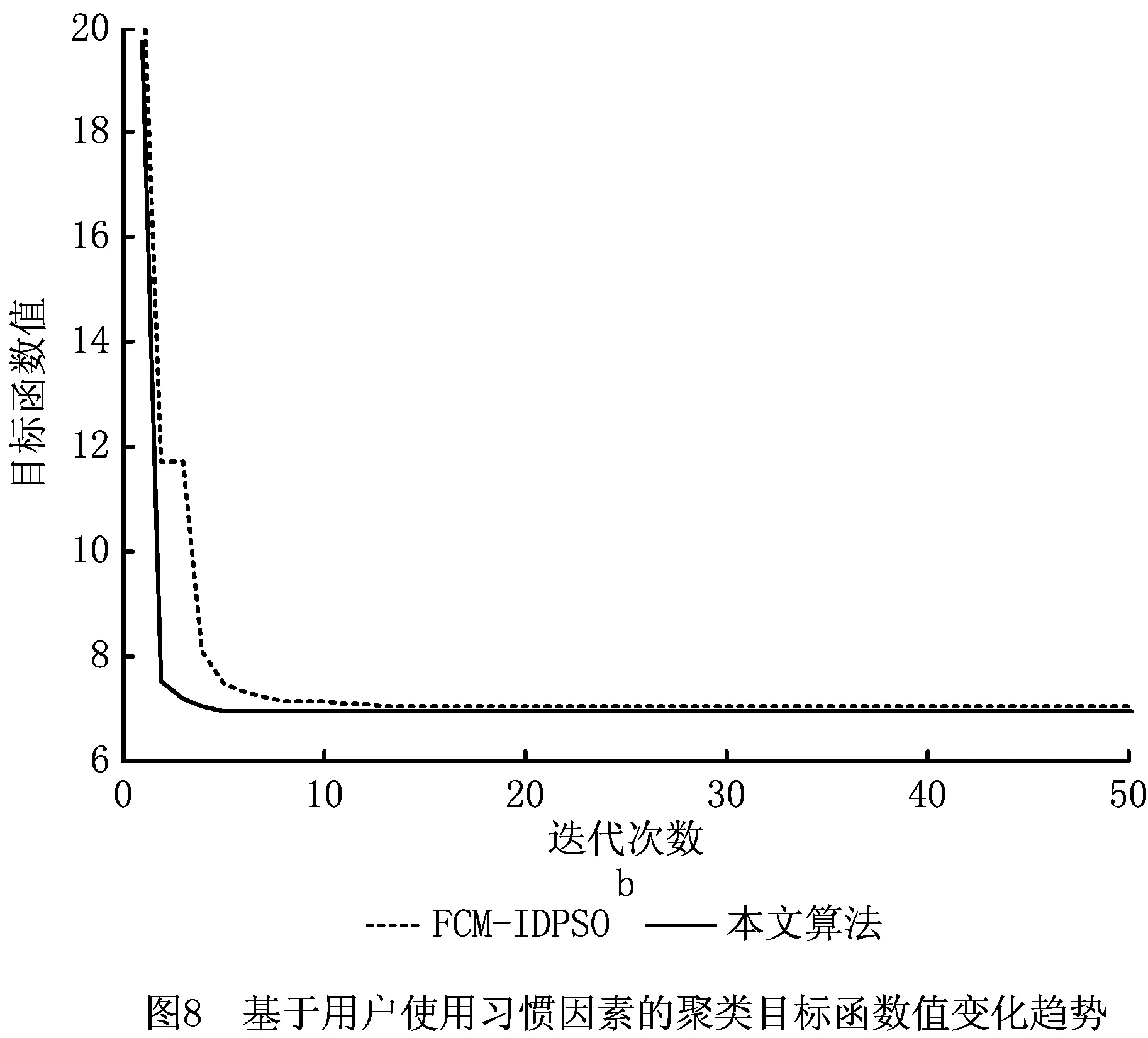
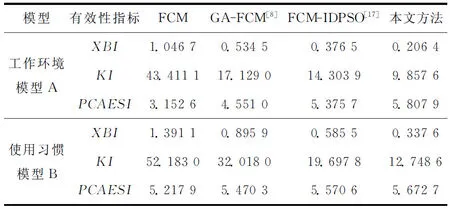
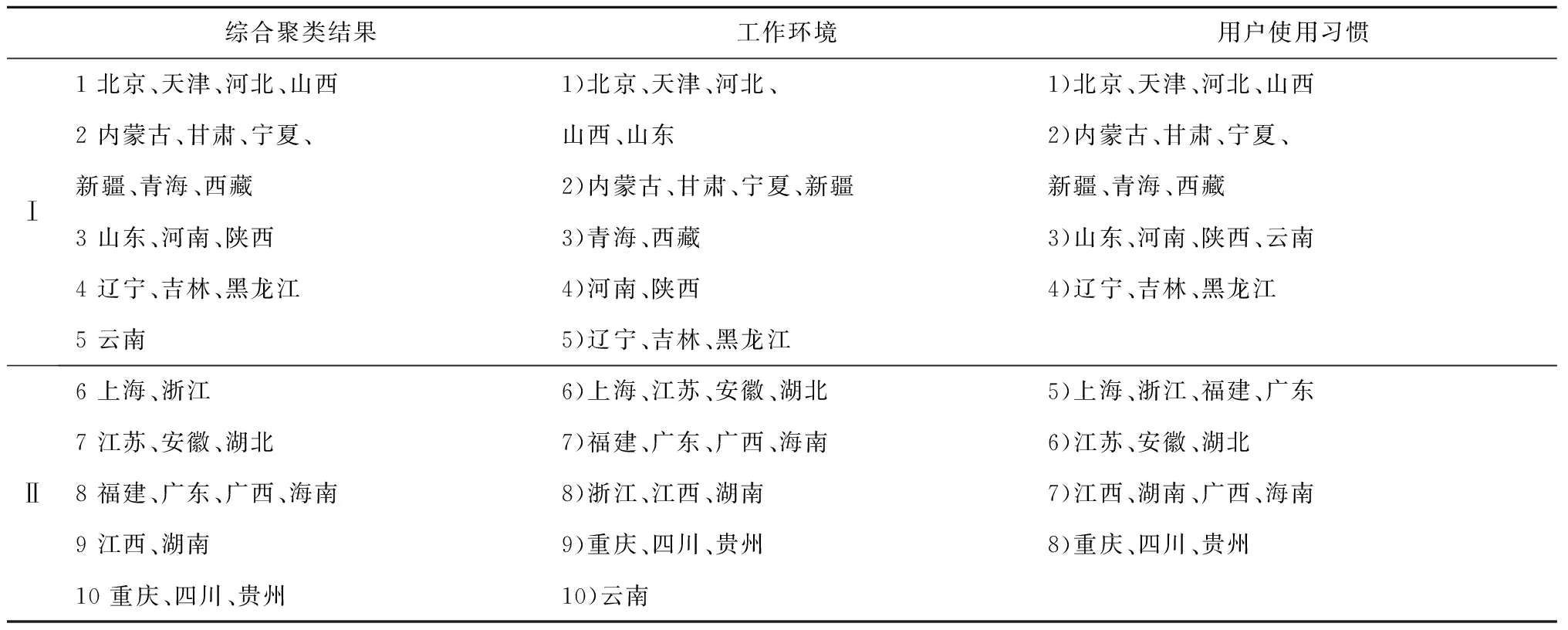
因为数据的聚类问题可以转化为一个非线性优化问题,所以空调使用可靠性区域粒度划分问题实际上是一个目标优化问题,以上述模型Α={Οks(t)|k=1,2,…,n;s=1,2,…,m;t=1,2,…,T}为例,若n个空调地域样本划分为c(1 Dik=α*·dik(AQED)+β*· dik(ISED)+γ*·dik(VCED)。 (4) 满足以下约束条件: s.t. uik∈[0,1],1≤i≤c,1≤k≤n。 (5) 式中:m为模糊指数;Dik表示样本οk到聚类中心vi的欧式距离。为减少信息损失,本文既考虑使用可靠性各影响因素的绝对水平,还分析其动态发展趋势,采用面板数据相似性指标对FCM中的距离进行优化,即Dik不再仅是以往简单的绝对量距离dik(AQED),还涵盖了两者间的增速距离dik(ISED)和波动距离dik(VCED),其中α*,β*,γ*分别表示3种距离相应的权重系数,且满足α*+β*+γ*=1。各距离的计算方法,详见文献[2]。 采用FCM算法进行聚类,可以得到第i类聚类中心vi和空调地域样本ok到聚类中心vi的隶属度uik: (6) (7) 经过上述不断迭代,得到最终的聚类中心和隶属度矩阵,从而确定所有样本的划分。然而,由于FCM算法本身存在不足以及模型Α,Β的高维度特性,很可能导致其只能找到局部最优解,因此有必要设计更优的算法以提高FCM的聚类性能。 为了求解上述空调使用可靠性区域聚类模型,提出IDCGAFCM算法。IDCGAFCM是在CGA和FCM的基础上改进的一种混合聚类算法,它在CGA中引入了信息熵理论,并采用动态交叉和基于熵的两阶段变异算子,使改进的IDCGA较好地提升了群体多样性,增强了算法的全局搜索能力;同时根据元胞遗传群体熵的变化判断当前的收敛程度,确定优选元胞个体执行FCM的操作时机,增强其局部搜索能力,从而在提高聚类精度的同时加快算法收敛速度。 CGA将元胞自动机理论和GA二者有机结合起来,种群中所有个体都排列在一个空间d维网格(d=1,2,3)中,每个个体放置在一个元胞网格位置内,且只与其相邻个体进行选择、交叉、变异等操作[25]。本文采用二维网格和元胞Moore邻域类型。CGA限定个体的遗传操作只发生在元胞邻域内,因此具有比GA更好的全局搜索能力,在一定程度上摆脱了GA解决复杂问题时易早熟收敛的困境,但它没有考虑进化过程中所有个体间的动态影响,即忽略了个体生死状态对进化产生的影响。而文献[27]通过实验表明,演化规则的引入有利于改善群体多样性和进行全局探索。因此,本文引用这种中等密度分布的演化规则建立动态环境来同步更新个体的状态。 算法采用基于聚类中心的编码方式,即每个元胞网格位置上的个体由c个聚类中心组成。设样本特征维数为d,元胞种群Q={x1,x2,…,xp,…,xM}(1≤p≤M),则每个个体基因矢量具有c×d维编码,即xp采用如下编码结构 xp=[xp,1xp,2…xp,dxp,d+1xp,d+2… xp,2d…xp,c×(d-1)+1xp,c×(d-1)+2…xp,c×d]。 (8) 式中:前d个量化值表示第一个d维的聚类中心,第d+1~2d个量化值表示第二个d维的聚类中心,依此类推。另外,每个个体还有一个对应的适应度值FIT(xp), (9) 式中:n为样本数,οk为输入样本。由式(9)可知,聚类目标函数值越小,聚类效果越好,适应度值FIT(xp)越大。经过若干代后,当FIT(xp)达到最大时,就可以获得最优的划分和聚类中心。 聚类中心初始值的选择已被证明对聚类质量有很大影响[28]。然而现有基于智能优化算法的聚类算法大多采用随机初始化的方法,具有一定的盲目性,可能会产生一些与数据集无关的簇类。因此,本文利用Arnold映射[29]具有遍历均匀性好的特性,将其产生的混沌序列替代随机初始化的聚类中心,以得到多样性好的初始种群。Arnold映射表达式为 (10) 利用Arnold映射产生的初始个体表示为 xpj=xjmin+αn(xjmax-xjmin)。 (11) 式中:αn,βn∈[0,1],αn为迭代至n步时的混沌变量; mod 1表示取余运算;xpj表示个体xp的第j维变量;[xjmin,xjmax]为第j维变量的取值范围,且xjmin和xjmax可由给定数据集各维度特征对应的最大值和最小值统计得到。重复上述迭代过程,直到产生群体规模为M的初始种群,从而最大程度地利用数据集的属性信息,同时使所有个体尽可能均匀分布在整个搜索空间。 CGA中的交叉、变异等遗传操作对其优化性能有显著影响,且交叉概率Pc、变异概率Pm极大程度地决定着其是否能有效地求解或收敛到最优解。虽然已有文献提出了关于Pc和Pm选择的指导方针[30],但这些结论是通过一些特定问题的实证研究获得的,只针对具体特定的问题才适用。实际上,最优的Pc和Pm因优化问题的不同而变化,甚至在进化过程的不同阶段也会不同。但是现有研究中,交叉和变异操作一般都事先设置固定的Pc和Pm,过高的概率会破坏优势个体,过低的概率又会导致算法收敛到局部极值。CGA的搜索过程是一个极其复杂的非线性过程,Pc和Pm采用固定值或简单的线性变换均不利于找到最好解。此外,生物进化也表明,Pc和Pm取决于进化状态而且应与其相适应[31]。因此,设计一个能够自适应调整Pc和Pm的动态更新策略至关重要。针对该问题,本文综合考虑种群当前进化状态以及个体与最优个体之间的距离,从全新的角度构建动态交叉、两阶段动态变异算子,使改进后的IDCGA能够避免早熟,收敛到局部最优。 2.3.1 动态交叉 为了能够自适应调整IDCGA的交叉概率,首先基于S型函数模型构建Pc的动态更新策略。设favg为第t代种群的平均适应度值,fmax为第t代种群的最高适应度值,f(xi)为待交叉个体的适应度值,fmax-f(xi)表示待交叉个体与最优个体间的距离,fmax-favg在一定程度上反映当前种群的进化状态,则第t代的交叉概率 (12) 2.3.2 基于熵的两阶段动态变异 由于在早期进化阶段,群体多样性维持在较高水平;但是随着搜索的进行,群体在后期有可能趋于聚集,导致群体多样性降低,算法收敛到局部最优。因此,维持种群多样性是提高IDCGA全局探索能力的有效手段,有必要分析研究IDCGA在进化过程中群体多样性的变化规律,并且根据群体多样性的变化设计两阶段的动态变异操作。 为此,将信息熵[26]引入元胞群体空间,用于度量群体多样性和指导搜索过程。种群熵DE(t)等于各位编码(基因)熵DEl(t):l=1,2,…,L的均值: (13) (14) 式中:al,bl为个体x第l维编码的最小值和最大值。 综上所述,待变异个体xi第t代的变异概率 (15) 式中:γ用于约束变异概率,可通过实验分析IDCGA对参数γ的敏感度而确定;Pm(i)为自适应概率, Pm(i)=φmax· (16) (17) 式中:N(0,1)为正态分布随机数;α(t)为自适应调节的变异步长。由于算法在进化初期需要以较大的步长搜索以确保全局搜索能力,进化后期则需要以较小步长搜索以确保局部搜索能力,因此对α(t)设计如下动态调整方法: α(t)=α(0)×exp(-κt/Tmax)。 (18) 式中:α(0)为初始步长;κ为时间常数;t为当前时刻;Tmax为最大迭代次数,根据具体的聚类问题设定。因此,所构建的两阶段变异操作充分利用元胞遗传群体的熵与S型函数模型的特性,有效克服了以往变异操作中恒定概率和固定变异步长的缺点。 FCM算法比IDCGA算法计算简单、收敛速度快,但易陷入局部极值,因此本文将IDCGA和FCM有机结合形成一种混合算法IDCGAFCM,其基本原理是充分利用IDCGA与FCM的优点,使算法的全局探索与局部寻优达到更精确的平衡,从而提高聚类效率和精度。 实现IDCGA和FCM有效结合的关键是确定FCM的操作时机以及如何执行FCM操作。实际上,在早期随机搜索阶段,算法应加强全局探索能力,这时只需充分利用IDCGA全局搜索能力强的优点,不需要执行FCM;在进入后期收敛阶段后,算法应加强局部寻优能力,这时引入FCM可以充分利用其特点,加快算法的收敛速度。 (1)首先将所有个体按照适应度高低进行排序,采用黄金分割法对个体进行优选,只对部分选中的38.2%较优秀元胞个体进行FCM操作。对于选中的元胞个体,按照以下FCM进行优化: 1)设置τ=0,最大迭代次数Gd,解码每个个体得到聚类中心。 2)利用式(6)计算隶属度。 3)利用式(7)计算聚类中心。 4)如果τ≤Gd,则转2);否则,用式(9)计算适应度值,并更新种群。 (2)其余未被选中的61.8%元胞个体不需执行FCM,仍保持原有种群结构进行全局搜索,从而兼顾了算法全局探索和局部寻优两者的平衡。 综上所述,IDCGAFCM算法的流程图如图2所示。 2.5.1 测试数据集 为了验证本文IDCGAFCM算法对低维数据和高维数据的分类性能,采用UCI数据库的Iris,Heart disease,Wine,Glass,Image segmentation和Landsat Satellite[32]6组标准数据集作为测试样本,分别利用本文提出的IDCGAFCM算法、FCM、GA-FCM[15]及FCM-IDPSO[24]对上述测试样本进行计算,并分析比较4种算法的聚类性能。 采用的测试数据集及主要特征如表1所示。 2.5.2 算法聚类结果及分析 从平均值、最差解、最好解、最优值标准差和收敛时间等方面进行100次实验,度量算法的收敛速度和稳定性能。仿真测试中算法的主要参数取值如表2所示。 表3所示为4种算法对低维数据的聚类结果,其中加粗数据为最优值。图3所示为各算法对低维(Iris)数据聚类时的目标函数值变化曲线。分析表3可以看出,针对同样的低维数据样本,本文IDCGAFCM算法找到的解比FCM,GA-FCM,FCM-IDPSO更好,在绝大多数情况下都能获得最高的聚类精度,FCM在短时间内陷入局部最优。虽然对比算法在一些数据集上也可以获得较好的性能,如GA-FCM和FCM-IDPSO优于FCM,尤其是FCM-IDPSO在Iris和Heart上的表现,但其不能每次都完全找到最优解,且IDCGAFCM算法的平均值、最优值标准差都最小,表明该方法的稳定性优于其他3种算法。 表3 4种算法对低维数据的聚类结果与收敛时间比较 表4所示为4种算法对Glass,Image segmentation和Landsat Satellite 3个高维数据的聚类结果,其中加粗数据为最优值,图4所示为各算法对高维(Image)数据聚类时的目标函数值曲线。从图4可以看出,对于高维度特征数据聚类问题,IDCGAFCM能够有效跳出局部最优,得到更好的聚类结果,其原因是IDCGAFCM的全局搜索能力优于GA-FCM及FCM-IDPSO。正如表4所示,IDCGAFCM的各项数据均显著优于其他3种方法,表明新方法具有更好的聚类精度和稳定性。各算法对高维数据聚类所用的时间还显示,IDCGAFCM较FCM-IDPSO和GA-FCM减少了约60%~80%,因此在实际工程问题中更具竞争力。 表4 4种算法对高维数据的聚类结果与收敛时间比较 综合表3和表4可知,IDCGAFCM对低维和高维数据的聚类精度、收敛速度和求解的稳定性明显优于其他3种方法,而且随着样本维数的增大,IDCGAFCM的优势更为突出,原因在于该算法有效结合了IDCGA和FCM的优点。因此,在解决具有高维度特征的复杂数据集聚类问题时,本文算法相比FCM,GA-FCM和FCM-IDPSO具有优势。 采用IDCGAFCM对产品使用可靠性进行区域粒度划分,基本步骤如下: 步骤1通过分析使用可靠性影响因素分别提取工作环境和用户使用习惯的关键影响因素,建立各影响因素的量化模型;选择产品使用可靠性区域划分数目的最小值cmin和最大值cmax,面向工程实践领域,划分数目c应满足cmin≤c≤cmax。 步骤2根据选取的区域样本数量n、最大时间长度T,对所有数据进行标准化,进而构建产品使用可靠性基于工作环境影响因素模型(模型A)和基于用户使用习惯影响因素模型(模型B),从c=cmin到c=cmax进行循环迭代。 (1)根据划分数目c和聚类特征的维度d确定基因编码长度L,采用Arnold映射初始化M个代表聚类中心矩阵V={v1,v2,…,vc}的元胞个体,每个个体xp代表一种可行的区域划分模式。 (2)按照IDCGAFCM算法的流程分别对模型A和模型B进行聚类计算,最终获得适应度最优的JACR值。由于问题的复杂性,很难找到最优解,在保持其他参数不变的条件下,终止迭代次数设置为10 000,收敛阈值ε=10-6。 (3)对最优JACR值对应的个体基因编码进行解码后获得聚类中心,分配对应的隶属度矩阵U=(uik)c×n。比较区域样本Οk(1≤k≤n)对每个簇类的隶属度值,将Οk划分到隶属度最大的簇类中。如果c=cmax,则算法终止;否则c=c+1,转(1)。 经过IDCGAFCM计算后,模型A和模型B的每种粒度层次下都有一个最优JACR值对应的聚类结果,这时可利用本文的评价准则对其进行评价,从而确定两者的聚类数和最优聚类结果。 步骤3综合模型A和模型B的聚类结果,获得产品使用可靠性在工作环境和使用时间上最具一致性的区域分布。 (1)将模型A和模型B的聚类结果有效结合起来,均隶属于同一簇类的多个样本被视为初始类,无法确定归属类别的样本被视为未归类,独立成组的样本被视为独立类。 (2)将每个包含两个及以上样本的簇类表示成聚类中心的方式,其值通过式(6)计算得到。 (3)将计算所得的聚类中心与单个样本一起视为总样本,利用IDCGAFCM再次进行聚类分析。 (4)当IDCGAFCM收敛或达到最大迭代次数时输出聚类结果,即为使用可靠性最优的区域粒度划分方案。 3.2.1 聚类评价指标 聚类有效性指标已被证明是度量不同聚类划分优劣和确定最佳聚类数的一类有效方法[33-34]。鉴于采用单一的指标难以确定最优聚类划分,本文有必要采用多项有效指标评价聚类质量。因此,下面既采用仅考虑模糊划分中隶属度信息的分类系数PC和平均模糊熵PE两个有效性指标[35],也选用同时考虑数据集几何结构和隶属度信息的XBI,KI和PCAESI[34]3个有效性指标进行使用可靠性区域粒度划分优劣的检验,并确定最佳聚类数。 (1)分类系数和平均模糊熵 PC和PE指标仅考虑了隶属度信息,且PC值越大,PE值越小,其聚类划分结果越好。 (2)XBI指标 该指标包含了隶属度信息和数据结构的几何属性,分子用于度量紧致性,分母用于度量分离度,且XBI值越小,聚类效果越好。 (3)KI指标 KI(c)= KI指标同时使用隶属度和聚类划分的几何结构信息,且KI值越小,聚类效果越好。 (4)PCAESI指标 该指标的第一项用来度量紧致性,第二项用来度量分离度。当PCAESI值最大时,聚类结果最优。 3.2.2 优势划分的确定 按上述过程对使用可靠性区域粒度划分结果进行检验,即在其他条件不变时,使用不同聚类数分别运行IDCGAFCM算法,同时利用5个有效性指标对其进行评价。当指标值达到最优时,得到的聚类结果即为最优粒度划分,相应的聚类数目即为模型A或模型B下合适的c值,从而确定最优的使用可靠性区域粒度划分方案。每组均代表了使用可靠性水平最具一致性的优势区域划分,每组包含的样本量的大小代表了产品具有相同使用可靠性水平的区域覆盖范围。 将上述IDCGAFCM算法及其在产品使用可靠性区域粒度确定过程中的具体实施步骤应用于中国省域空调使用可靠性的区域粒度划分问题,获得空调使用可靠性的最优区域粒度划分方案,以该空调使用可靠性的区域分布规律进行分析和讨论。 3.3.1 数据来源与指标选取 按照中国区域经济统计年鉴划分区域方法并鉴于数据的可得性,本文实例分析中所用的样本为除香港、澳门特别行政区和台湾省之外的中国大陆31个省级行政区划单位。因为国家统计局发布的关于城镇和农村居民家庭平均每百户空调拥有量以及城镇居民人均可支配收入和农村居民人均收入的统计数据截止到2012年,中国气象科学数据共享服务网发布的气象数据截止到2013年,所以样本区间的跨度选择2005~2012年。其中温度、相对湿度、日照、降水量和风速的数据来源于中国气象科学数据共享服务网发布的中国地面气候资料月值数据集、中国地面气候资料日值数据集;社会消费品零售总额增长率、空调平均消费倾向则根据《中国区域经济统计年鉴》(2005~2012年)的相关数据经计算得出。至此,本文分别构建了包括2005~2012年31个省级行政区划单位的基于工作环境影响因素和用户使用空调习惯影响因素的面板数据集模型A(31×8×48),B(31×8×24)。限于篇幅,表5和表6给出了部分研究数据。 表5 中国省域空调样本工作环境聚类特征数据 表6 中国省域空调样本用户使用习惯聚类特征数据 续表6 3.3.2 空调使用可靠性区域粒度划分的评价及结果分析 按照IDCGAFCM算法分别对模型A和模型B进行计算,算法参数设置为:种群规模M=100,空调区域样本数量n=31,终止评价次数Tmax=10 000,模型A的聚类特征维度d=384,模型B的聚类特征维度d=192,cmin=2,cmax=14。采用基于聚类中心的实数制编码生成初始种群,根据划分数目c渐进改变的实际要求,初始种群中每个个体基因矢量编码长度c×d也随之变化,编码设计为{y1,y2,…,yi,…,yc},其中yi表示第i个初始聚类中心且yi=(yi1,…yij,…,yid)。以模型B为例,yij则是由用户使用习惯第j维聚类特征对应的最大值和最小值及Arnold映射经式(11)计算得到的聚类中心初值,依此类推生成初始种群。 将表5和表6的数据导入编译后的程序环境中,从c=2,…,14依次进行迭代优化,得到不同聚类数目所对应的聚类结果。为此,同时采用5个不同的有效性指标对cmin=2和cmax=14之间的每个粒度层次下的粒度划分结果进行定量评价,以确定最优的粒度划分。各指标取值与聚类数目c两者的关系如图5和图6所示。 从图5可以看出,除PC和PE指标外,其余各项有效性指标均表明c=10时,聚类效果最佳。由图5a和图5b可知,对于仅考虑隶属度信息的PC和PE指标,当聚类数由2增加到14时,随聚类数的增大,各指标存在单调递增或递减的问题,难以准确辨别模型A的聚类数,主要原因是这些指标没有使用聚类划分的几何结构信息,缺少与模型A几何结构的直接联系,因此在准确评价基于工作环境影响因素的空调使用可靠性区域粒度划分质量和识别聚类数方面不太理想。而对于同时考虑模型A几何结构和隶属度信息的PCAESI,XBI,KI指标而言,由图5e可知,当聚类数由2增加到10时,PCAESI指标总体上处于上升的趋势;当c>10时,PCAESI又开始下降,表明c=10是最佳聚类数。从图5c和图5d可以看出,当聚类数由2增加到14时,XBI和KI指标在c=2,10处有两个明显的极小值点,实际上c=10时的XBI和KI指标仅大于c=2时的指标值,这也表明c=10是一个较优的聚类数目。因此,空调使用可靠性区域划分数目c取10是合理的,这也正是取多项评判指标的原因。同理,由图6可知,PCAESI,XBI,KI指标能够较全面地评价基于用户使用习惯影响因素的空调使用可靠性区域粒度划分的质量,因此最佳划分数目c应取8类。 依然采用GA-FCM,FCM-IDPSO和本文算法分别对基于工作环境影响因素和基于用户使用习惯影响因素的空调使用可靠性区域聚类进行运算。3种智能聚类算法在基于工作环境影响因素的空调使用可靠性分类数取10的情况下,其聚类目标函数的迭代过程如图7所示;在基于用户使用习惯影响因素的空调使用可靠性分类数取8的情况下,其聚类目标函数的迭代过程如图8所示。 从图7和图8可以看出,本文方法求解得到的聚类结果更好,且聚类时所用时间更少。为进一步说明在产品使用可靠性区域粒度划分的应用上,本文方法较其他方法具有一定的优越性,用上述4种方法优化PCAESI,XBI,KI3个有效性指标,各自独立进行30次运算,计算结果如表7所示。 由表7可以看出,针对同样的模型A或模型B,本文算法所得的XBI和KI指标值比FCM,GA-FCM,FCM-IDPSO更小一些,表明其聚类效果好于其他3种方法。表中数据还显示,本文算法得到的PCAESI值最大,也表明其聚类结果最优。因此,通过分析以上实验数据表明,在解决模型A和模型B的聚类问题时,本文算法较其他3种方法具有更好的聚类精度。 综合图7和图8及表7可知,与FCM,GA-FCM,FCM-IDPSO相比,本文算法在聚类效率和精度方面均表现出了一定的优势,因此采用本文算法求解使用可靠性区域聚类模型得到最优解,则适应度最优的元胞个体基因编码所代表的聚类中心矩阵V及对应的隶属度矩阵U即为最优的聚类结果。比较每个空调地域样本对聚类中心的隶属度,找出最大值,便可直观地决定该地域属于哪一个簇类(限于篇幅,未列出各地域样本所对应的隶属度矩阵,只列出相应的划分结果),空调使用可靠性单独基于工作环境和基于用户使用习惯因素进行划分的最优聚类结果如表8第2,3列所示。最后,按照步骤3综合两类聚类结果,得到二次聚类后的空调使用可靠性基于双重影响因素的最优区域粒度划分方案,如表8第1列所示。 表8 本文方法得到的空调使用可靠性的区域粒度划分方案 从表8可以看出,经过聚类后空调使用可靠性地域样本之间的关系比较明显,起到了良好的分类效果。从区域空调使用可靠性水平与工作环境和使用习惯的一致性等几个方面对上述10类区域进行考察和归纳,大致可以分为如下两个层次: (1)第Ⅰ层 从工作环境影响因素来看,北京、内蒙古、青海、河南、辽宁5类区域在全国排列中处于影响程度较低水平,这与基于月份的平均温度、湿度、日照、降水量指标考察的工作环境因素恶劣水平明显正相关关系。从用户使用习惯影响因素来看,北京、内蒙古、山东、辽宁4类区域空调使用可靠性受其影响的程度更小;考察空调在各个季度开机时间特征发现,山东、河南、陕西、云南4省的使用时间较为接近。综合两类影响因素来看,北京、内蒙古、山东、辽宁、云南5类区域受二者的影响程度较低,空调使用可靠性处于相对较高水平。 (2)第Ⅱ层 从工作环境影响因素来看,上海、福建、浙江、重庆5类区域的空调使用可靠性受其影响的程度较大;从用户使用习惯影响因素来看,上海、江苏、江西、重庆4类区域的空调使用可靠性受其影响的程度更大。总体来说,上海、江苏、福建、江西、重庆5类区域受工作环境和使用习惯两类因素影响的程度在全国排列中处于中上水平,空调使用可靠性处于相对较低水平。 本文针对产品使用可靠性区域粒度确定问题,建立了基于工作环境和用户使用习惯两类因素的多变量的高维聚类目标模型,基于CGA算法良好的多样性和全局搜索能力,以及FCM算法良好的局部搜索能力,有效结合这两种算法的特点互补长短,在CGA算法中引入信息熵理论和黄金分割优选策略,并采用动态的交叉和基于熵的两阶段动态变异算子,形成了一种混合聚类算法IDCGAFCM,以使聚类结果在精度和稳定性得到明显提高的同时大大减少其聚类所用的时间。IDCGAFCM与GA-FCM,FCM-IDPSO,FCM的性能对比结果验证了IDCGAFCM的有效性和可行性,并给出了其在产品使用可靠性区域粒度确定过程中的具体实施方法。最后将4种算法分别应用于空调使用可靠性区域聚类模型的求解,实例对比分析结果表明,本文算法比其他3种算法的效果有所改善,为解决空调使用可靠性区域粒度确定问题提供了一种新的方法。 与现有的空调使用可靠性区域粒度确定方法相比,本文所提方法可大幅减少设计人员的工作量及主观性因素的影响程度,而且科学精细的使用可靠性区域粒度研究也为空调产品可靠性设计、开展分区保修及实现保修策略的最优设计奠定了基础。未来将进一步改善该算法的性能,并将算法推广应用于其他类型家电产品的使用可靠性区域粒度的确定问题。2 动态优选元胞遗传模糊聚类算法
2.1 元胞遗传算法原理
2.2 初始种群的产生
2.3 遗传操作设计




2.4 IDCGAFCM算法原理




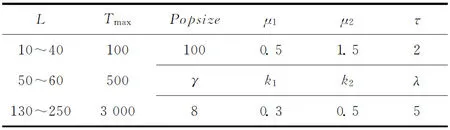
2.5 IDCGAFCM算法性能测试及结果分析




3 IDCGAFCM算法在使用可靠性区域粒度问题中的应用
3.1 实施步骤
3.2 聚类有效性评价及优势划分的确定
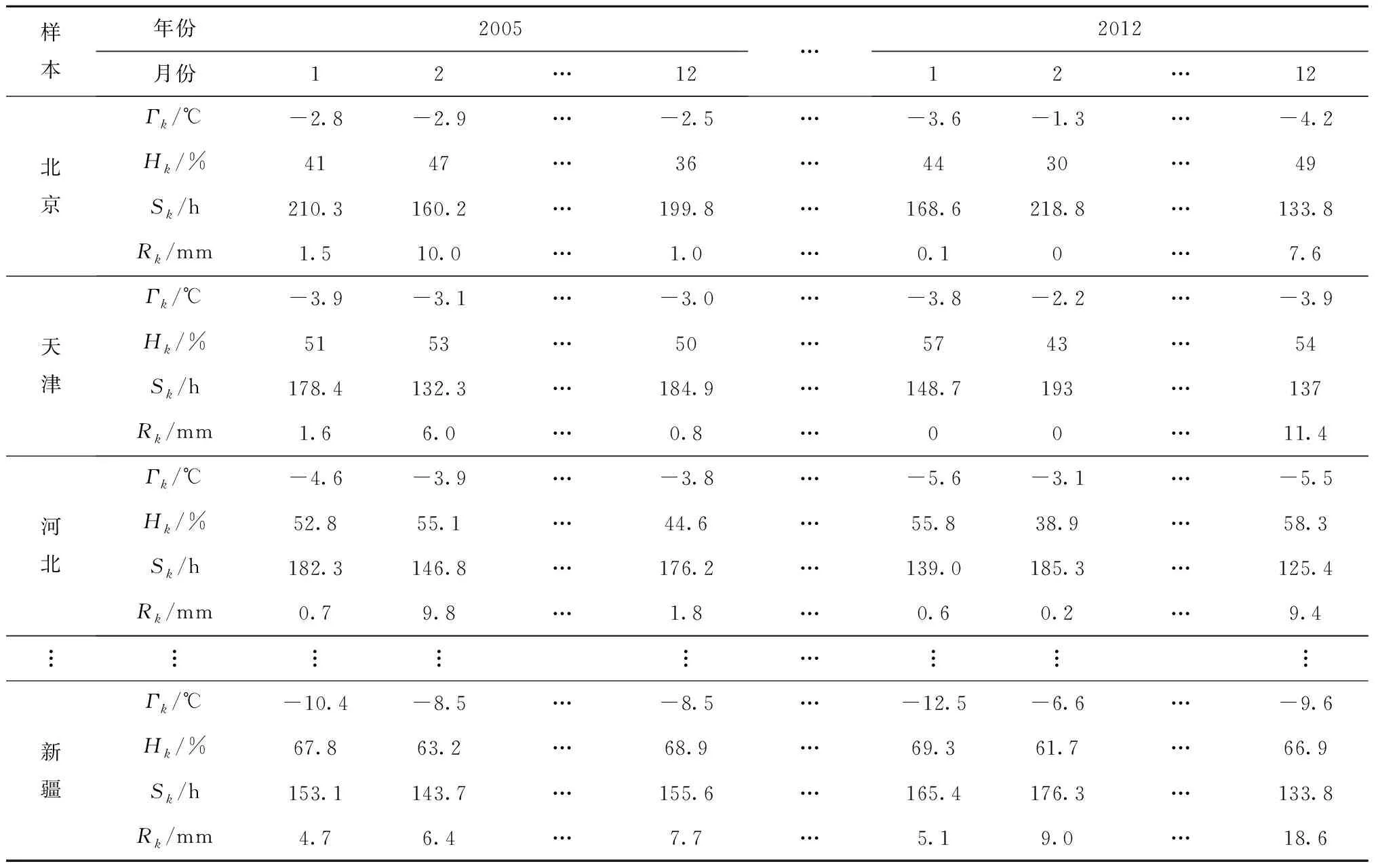
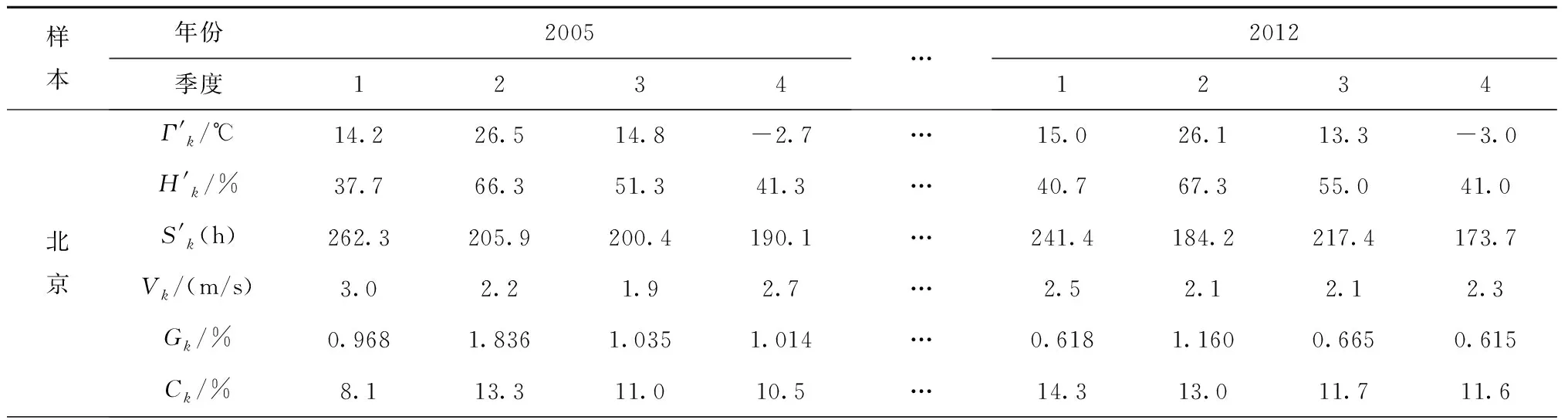
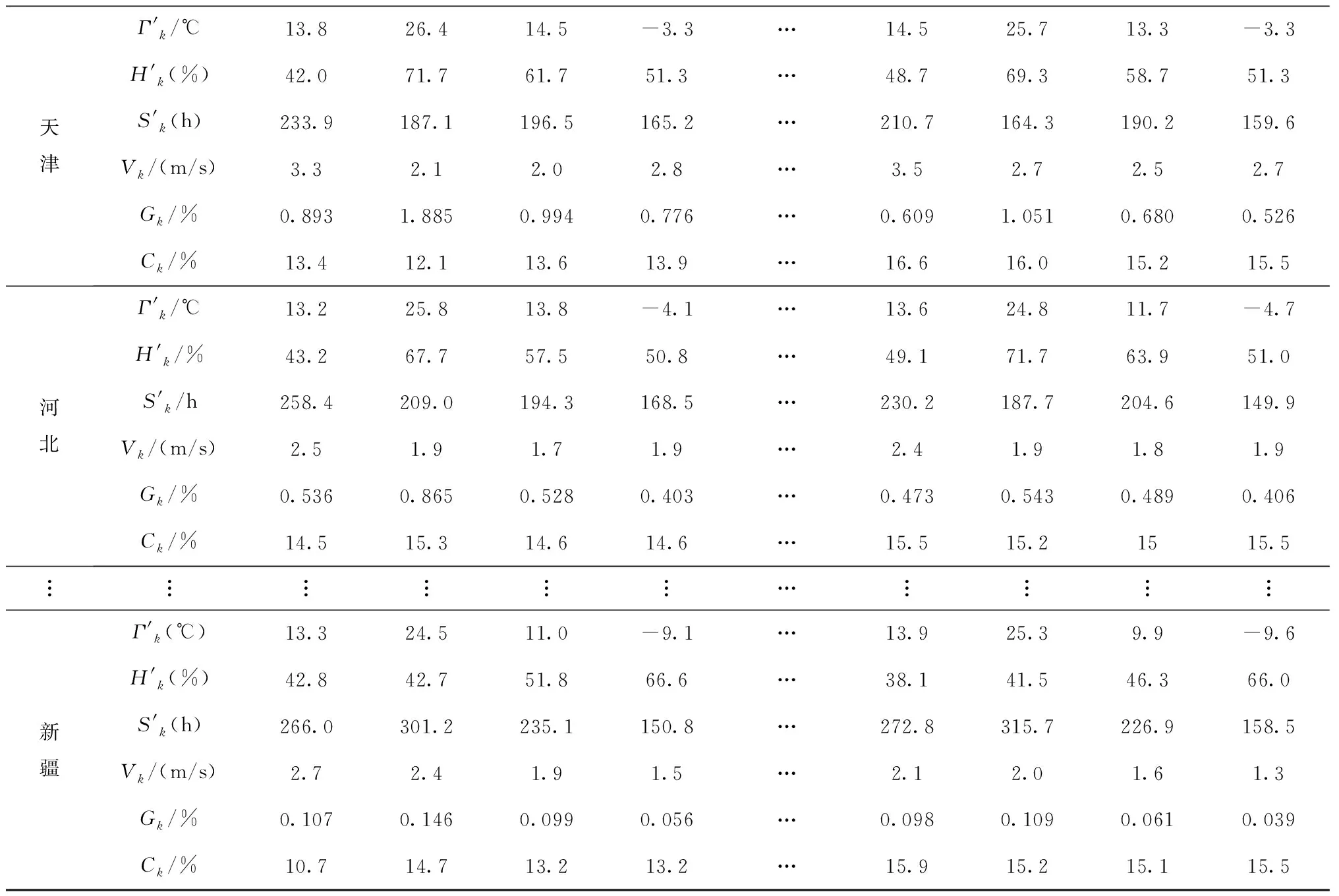
3.3 应用实例


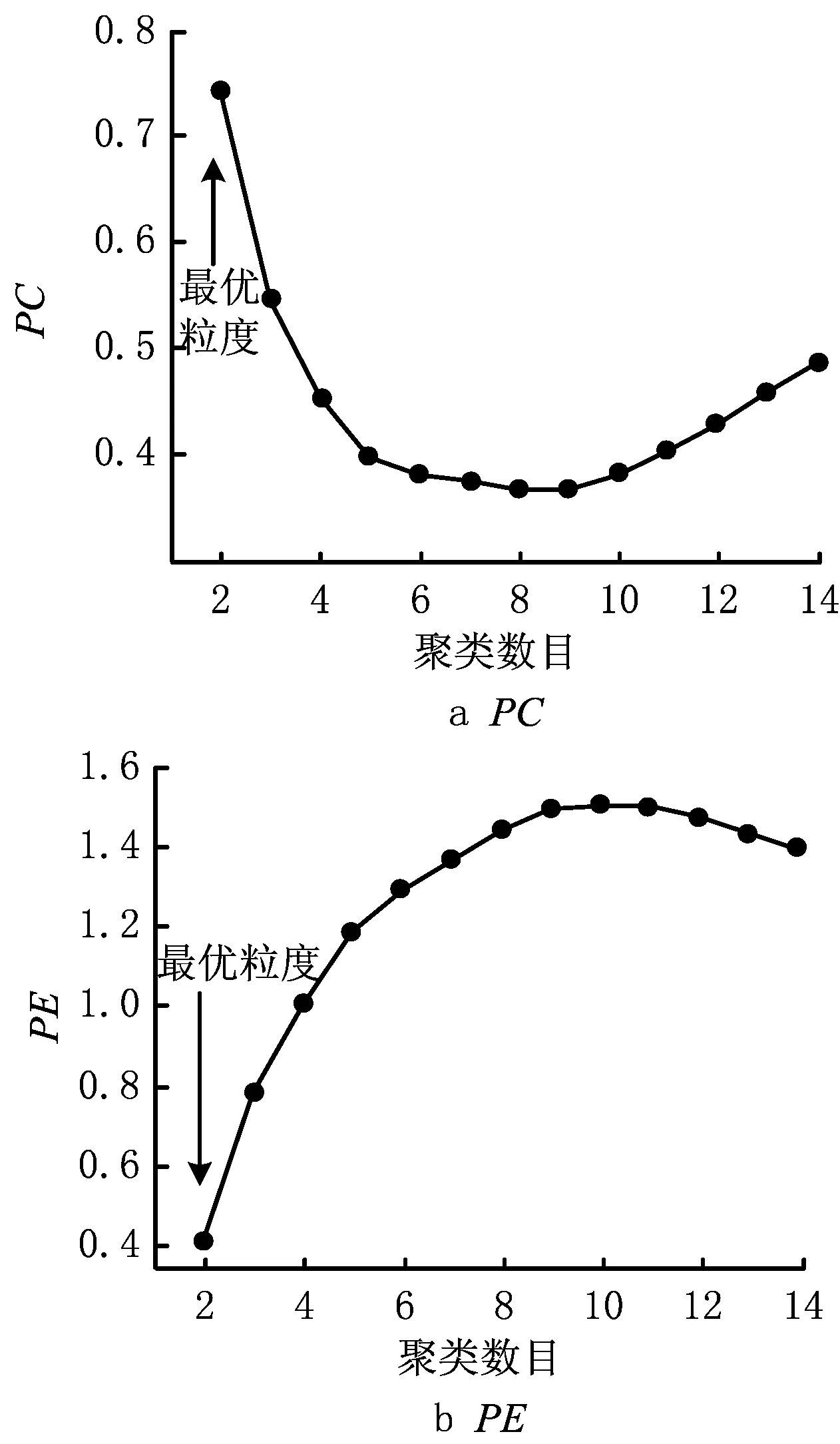
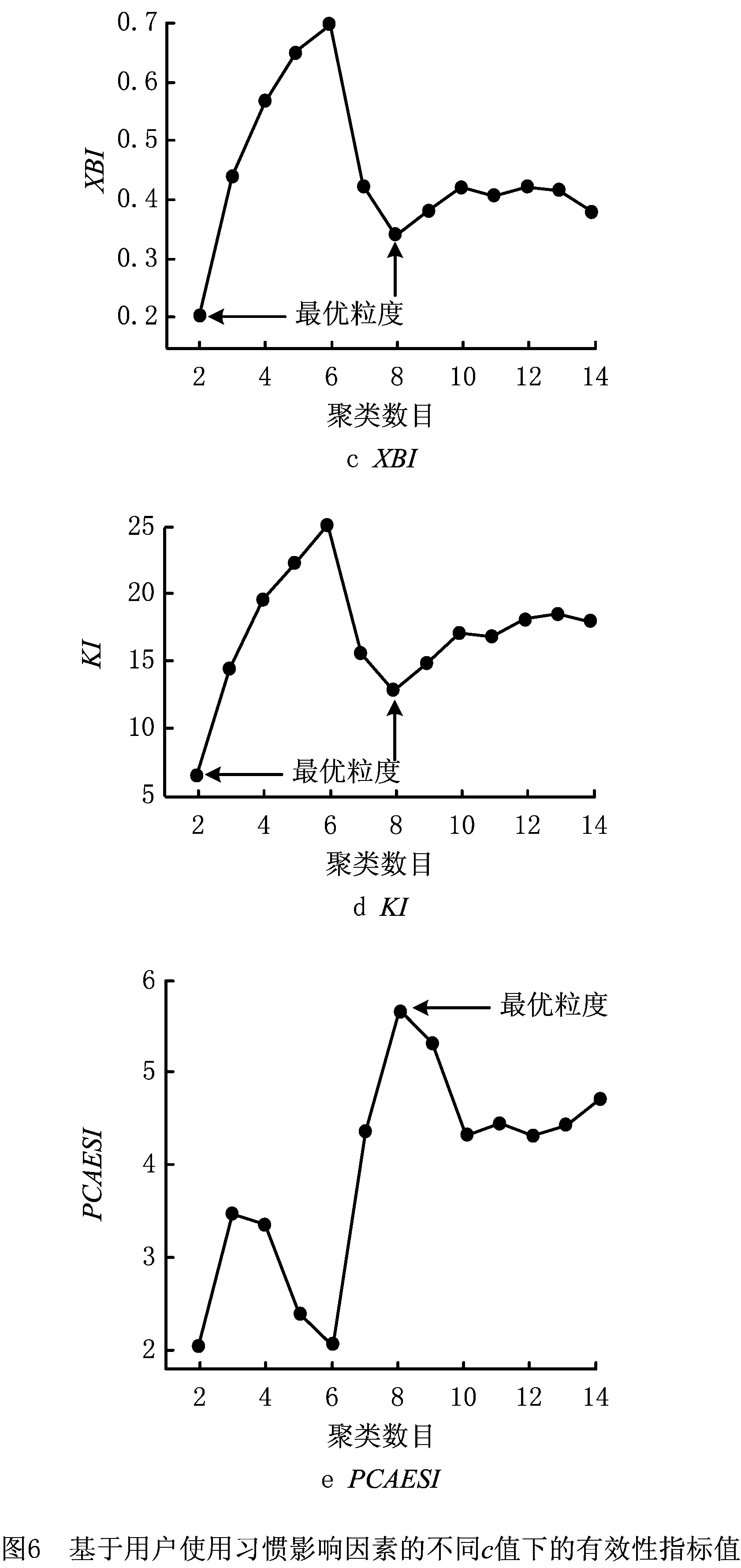
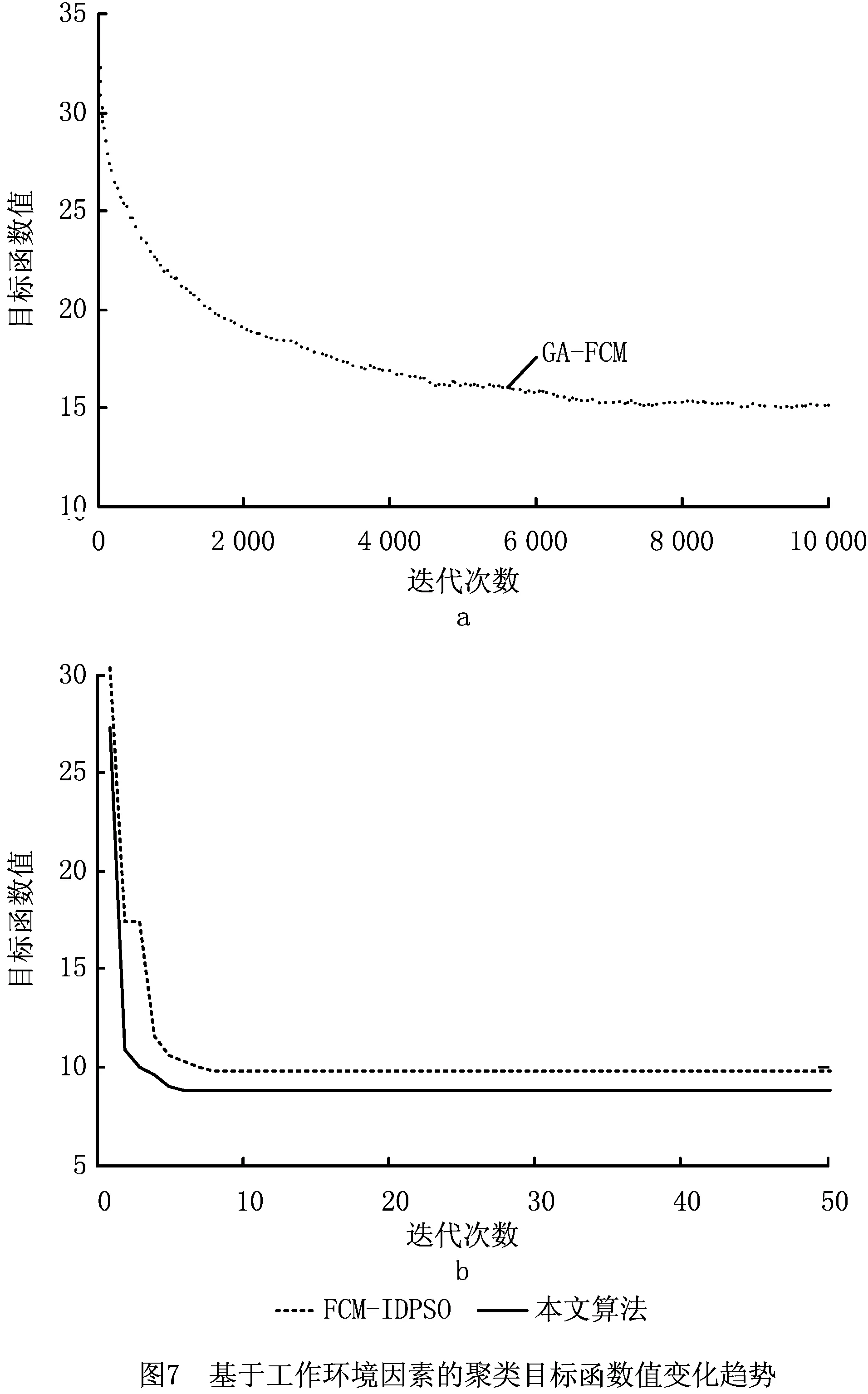
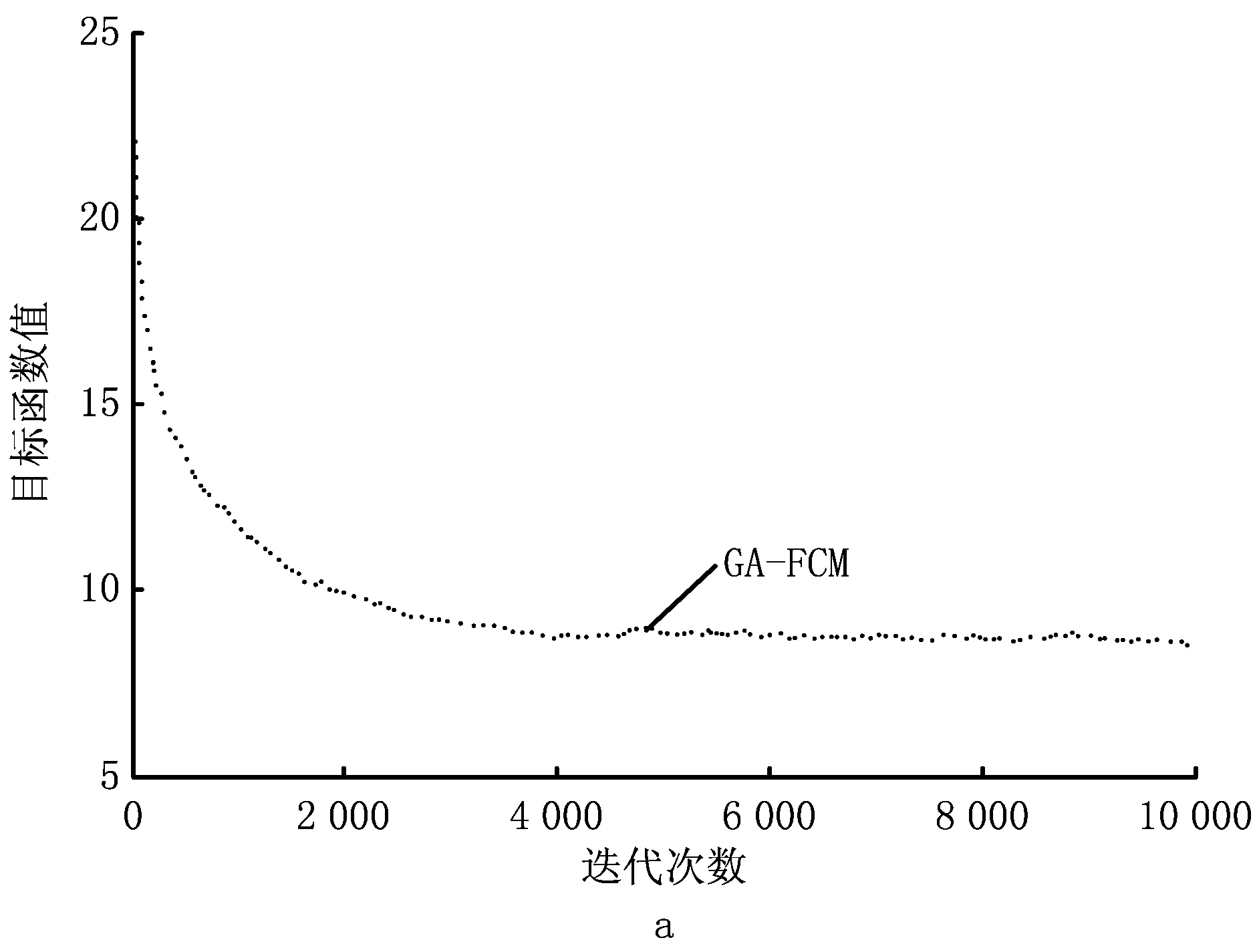
4 结束语
