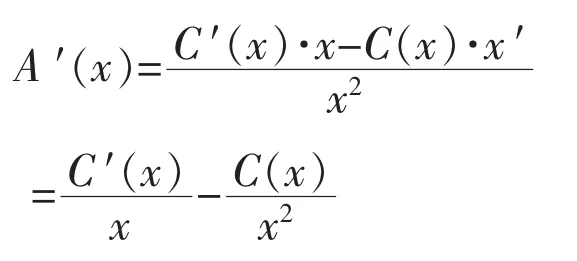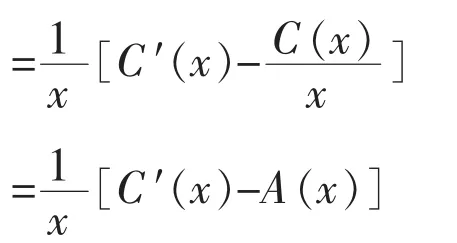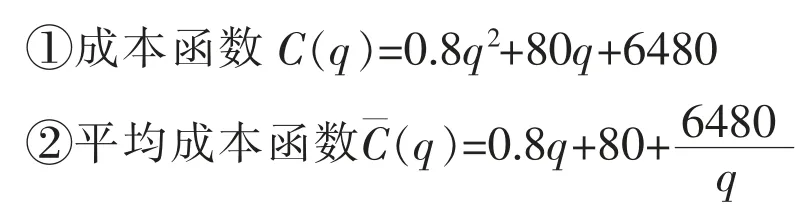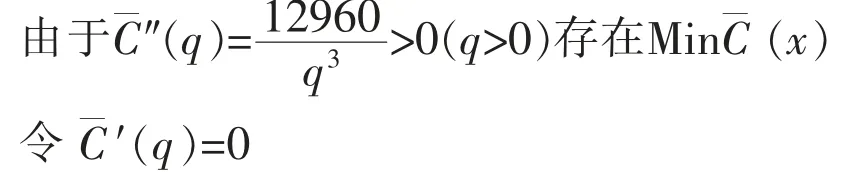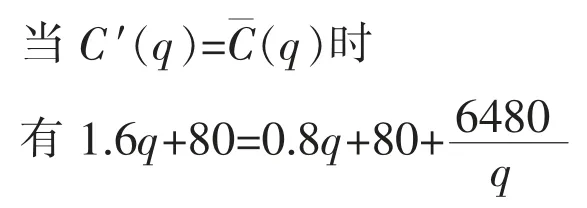浅议导数和边际在量本利经济分析中的应用
2020-08-20丁建华王毅成
◎文/过 涛 丁建华 王毅成
一、导数的概念和定义
(一)导数的概念
导数是一个数学概念, 导数的概念在于刻划瞬时变化率。导数作为函数的变化率,主要研究函数变化形态。 求导数的运算被称为微分运算,是微分学的基本运算。导数的概念和其他数学概念一样,是源于人类的实践。
导数的思想最初是由法国数学家费马在1629 年为研究极值问题而引入的。17 世纪英国数学家牛顿在研究物理变速运动物体的瞬时速度问题,采用了相同的研究思想。 17 世纪德国数学家莱布尼茨在研究几何曲线的斜率问题,也采用了相同的研究思想。
(二)导数的定义及表述式
设函数y=f(x)在点x0的某个领域内有定义,若极限存在,则称f在点x0处可导,称该极限为函数f在x0处的导数,记作f(x0)。
于是,导数的定义从数量关系上看,所反映的是函数的自变量的变化对相应的函数值变化快慢影响的程度,即变化率,也称为瞬时变化率;对数学表达式而言,所表达的是函数增量和自变量之比的极限问题。
二、“边际”概念提出的背景
随着市场经济的不断发展, 经济活动中的实际问题也愈加复杂, 简单的数学工具无法满足复杂的经济分析需要。 19 世纪70 年代, 经济学家在研究经济问题时发现了经济领域也存在大量的变化率问题, 为了充分利用数学工具,解决经济领域的变化率问题,提出了“边际”的概念,并定义“边际”是经济函数的一阶导数。
根据“边际”的定义,我们认为,“边际”既不是一个单纯的数学概念, 也不是一个单纯的经济学概念。 他是经济学和数学相结合的纽带和桥梁, 他是为了经济学和高等数学相结合而引入的新概念,“边际” 概念的引入使复杂变化的经济学问题应用导数来解决成为可能;“边际”概念的引入,开辟了高等数学应用的新领域, 从自然科学发展到社会科学;“边际”概念的引入,使复杂的经济分析走向定量化、精准化、简捷化、直观化。
三、边际的定义表达式及延伸应用定理
(一)边际定义表达式
函数f(x) 的一阶导数f′(x)称为f(x)的边际函数;在点x0的值f′(x0)称为f(x)在x0处的边际值。 记作:经济函数y=f(x)可导,边际函数My=f′(x)。
(二)边际延伸应用定理
如果f(x)有二阶导数存在,且f′(x)=0,若f″(x0)<0,则f(x0)是极大值,若f″(x0)>0,则f(x0)是极小值。 即:边际延伸应用的前提条件是f″(x)存在,且f″(x0)≠0。
四、边际原理在线性量本利经济函数的应用和思考
(一)应用边际定义进行边际计算
1.线性量本利经济函数表达式
(1)收入函数S=S(q)=Pq
(2)成本函数C=C(q)=Vq+F
(3)利润函数R=R(q)=Pq-Vq-F
其中:S收入C成本R利润
S(q)收入函数C(q)成本函数R(q)利润函数
q数量(变量)F产品固定成本(常数)
V单位产品变动成本(常数)P单位产品价格(常数)
2.线性量本利边际函数表达式及计算结果
(1)边际收入函数MS=S′(q)=(Pq)′=P
(2)边际成本函数MC=C′(q)=(Vq+F)′=V
(3)边际利润函数MR=R′(q)=(Pq-Vq-F)′=P-V
(二)根据边际的计算结果得出如下结论
1.边际收入=单位产品价格=P
2.边际成本=单位变动成本=V
3.边际利润=边际收入-边际成本=P-V
4.边际利润=单位产品价格-单位变动成本=P-V
5.边际固定成本等于零
(三)应用边际原理得出线性量本利盈亏
平衡分析法的简化计算公式

3.盈亏平衡时边际收入和销售价格S0′=P0=R0′+V
4.盈亏平衡时边际成本和单位变动成本C0′=V0=P-R0′
5.盈亏平衡时固定成本F0=R′(q)·Q
(四)线性量本利经济函数边际计算结果和结论的思考
1.从线性量本利经济函数有关边际计算结果和结论来看,存在一个共同的特点,他们的经济函数的一阶导数的计算结果均为常数,所以他们的二阶导数的计算结果均等于零,因此,根据边际延伸应用定理,线性量本利经济函数不符合边际延伸应用的条件:“f″(x)存在,且f″(x0)≠0”。 据此,我们不能应用利润最大化定理和平均成本最小化定理的有关方法和结论作为线性量本利函数的边际结论和方法,如不能应用“边际利润等于零,边际收入等于边际成本时, 实现的利润最大,此点对应的产量为利润最大时的最优产量”等非线性边际结论作为线性量本利函数的边际分析结论。 同时也不能将“边际利润等于销售价格减去单位变动成本”等线性量本利经济函数的边际分析结论推广应用到非线性量本利经济函数的边际分析中,在具体的边际分析中不能混淆,否则,必然会造成分析结论的错误, 在现实的经济生活中,这种混淆和错误时有发生,并且在现行的许多出版物中经常出现,因此这是一个值得研究和探讨的问题。
2.从线性量本利经济函数有关边际的计算结果和结论来看,还有一个共同的特点,就是都与“PV”有关系。 因此,在线性量本利经济函数的边际分析中,有必要引入“线性量本利经济函数边际PV 分析法”( 以下简称“PV分析法”) 。
(五)“PV 分析法”概述
1.边际利润等于零、边际收入等于边际成本(P-V=0),称为产量(销售量)的增减对弥补固定成本没有贡献(“零贡献”)。 对盈利企业来说,产量(销售量)的增减不增盈,对亏损企业来说,产量(销售量)的增减不减亏。
2.边际利润大于零、边际收入大于边际成本(P-V>0),称为产量(销售量)的增减对弥补固定成本有“正贡献”。 对盈利企业来说,产量(销售量)的增加会增盈;产量(销售量)的减少会减盈。 对于亏损企业来说,产量(销售量)的增加会减亏;产量(销售量)的减少会增亏。
3.边际利润小于零、边际收入小于边际成本(P-V<0),称为产量(销售量)的增减对弥补固定成本有“负贡献”。 对盈利企业来说,产量(销售量)的增加会减盈;产量(销售量)的减少会增盈。 对于亏损企业来说,产量(销售量)的增加会增亏;产量(销售量)的减少会减亏。
(六)边际原理在线性量本利经济函数的实例应用
1.边际利润大于零、边际收入大于边际成本(P>V 型)的实例应用
分析采用的资料:A 产品销售价格260元/个, 单位变动成本180 元/个, 固定成本660 万元/年,销售量20 万个/年,生产能力25万个/年。
(1)根据分析资料计算的边际数据
①边际收入MS=S′(q)=P=260 元/个
②边际成本MC=C′(q)=V=180 元/个
③边际利润MR=R′(q)=S′(q)-C′(q)=P-V=80 元/个
④边际固定成本MF=F′=0
⑤盈亏平衡时边际利润R0′=FQ=33 元/个
⑥盈亏平衡时边际收入和销售价格S0′=P0=R0′+V=213 元/个
⑦盈亏平衡时边际成本和单位变动成本C0′=V0=P-R0′=227 元/个
⑨盈亏平衡时固定成本F0=R′(q)·Q=1600 万元
⑩销售收入5200 万元
⑪销售成本4260 万元
⑫销售利润940 万元
(2)分析
①边际利润的一般经济含义是当销售量为q个单位处于某一水平有微小变化时利润的瞬时变化率;可以表述为:销售量为q个单位时,再增加(减少)销售一个单位时利润的增加(减少)量,边际利润等于利润函数的一阶导数。由于线性量本利经济函数的特性,根据边际定义得出结论: 边际利润等于销售价格减去单位成本。 A 产品此时边际利润等于80 元/个,边际利润大于零,属于具有“正贡献”产品,因此,增加销售量会使企业增产增收,减少销售量会使企业减收,甚至亏损。 如果销售量增加5 万个, 在其他因素不变的情况下,可以增加利润400 万元;如果销售量减少5 万个,在其他因素不变的情况下,销售利润减少400 万元;盈亏平衡的产量8.25 万个/年,如果销售量低于8.25 万个,企业生产本产品将发生亏损。
②边际成本的一般经济含义是当销售量为q个单位处于某一水平有微小变化时成本的瞬时变化率;可以表述为:销售量为q个单位时,再增加(减少)销售一个单位时成本的增加(减少)量,边际成本等于成本函数的一阶导数。由于线性量本利经济函数的特性,根据边际定义得出结论: 边际成本等于单位变动成本。该产品目前的边际成本(单位变动成本)为180 元/个,盈亏平衡时的边际成本(单位变动成本)是227 元/个,也就是说,该产品边际成本上升26.11%,生产该产品将没有利润; 该产品边际成本由180 元/个上升到260元/个,边际利润为零,该产品变成“零贡献”产品。
③边际收入的一般经济含义是当销售量为q个单位处于某一水平有微小变化时收入的瞬时变化率;可以表述为:销售量为q个单位时,再增加(减少)销售一个单位时收入的增加(减少)量,边际收入等于收入函数的一阶导数。由于线性量本利经济函数的特性,根据边际定义得出结论: 边际收入等于销售价格。 该产品目前的边际销售收入(销售价格)为260 元/个,盈亏平衡时的边际销售收入为213 元/个,也就是说,该产品边际销售收入下降18.07%,生产该产品将无利可图;该产品边际销售收入由260 元降为180 元/个,边际利润为零,该产品变成“零贡献”产品。
④降低固定成本,可以直接增加利润,该产品固定成本20%, 盈亏平衡时边际利润由33 元/个下降为26.40 元/个,也下降了20%,该产品盈亏平衡时固定成本为1600 万元,说明在其他因素不变的情况下, 固定成本增加142.42%,生产该产品才会亏损。
⑤边际固定成本为零, 表明固定成本不随销售量的变化而变化, 但单位固定成本随销售量的变化而变化,并且成反比关系,销售量20 万个时,单位固定成本33 元/个;销售量25 万个时,单位固定成本26.4 元/个;销售量15 万个时,单位固定成本44 元/个。
2.边际利润等于零、边际收入等于边际成本(P=V型)的实例应用
分析采用的资料:产品销售价格220 元/个,单位变动成本220 元/个,固定成本660 万元/年,销售量20万个/年,生产能力25万个/年。
(1)根据分析资料计算的边际数据
①边际收入MS=S′(q)=P=220 元/个
②边际成本MC=C′(q)=V=220 元/个
③边际利润MR=R′(q)=S′(q)-C′(q)=P-V=0
④边际固定成本MF=F′=0
⑥盈亏平衡时边际收入和销售价格S0′=P0=R0′+V=253 元/个
⑦盈亏平衡时边际成本和单位变动成本C0′=V0=P-R0′=187 元/个
2.1.2 文献报告 文献学习是科学研究的基础,通过查阅文献可以快速掌握专业知识,了解相关学科发展动态,从而有助于科研选题。由于专业不同,每位学生的研究内容也各有侧重,因而学生的文献学习具有各自特点,在一起交流有扩大知识面、互相启发、开阔研究思路的作用。如中医专业学生进行关于《四圣心源》医书中主张“中气之治”学术思想的探讨;中药专业学生进行鹿茸商品规格的分子鉴定技术、气相色谱—质谱联用技术等专题讨论。
⑨盈亏平衡时固定成本F0=R′(q)·Q=0
⑩销售收入 4400 万元
⑪销售成本 5060 万元
⑫销售利润 -660 万元
(2)分析
②降低边际成本(单位变动成本)是实现扭亏为盈的主要途径, 该产品的盈亏平衡时边际成本(单位变动成本)C0′=V0=187 元/个,在其他条件不变的情况下,边际成本(单位变动成本)下降15%以上,就能扭亏为盈。
③提高边际收入(销售价格)也是实现扭亏为盈的主要途径, 该产品盈亏平衡时边际销售收入(销售价格)S0′=P0=253 元/个,在其他条件不变的情况下, 销售价格提高15%以上就能扭亏为盈。
④降低固定成本,可以直接减少亏损,该产品固定成本降低20%, 盈亏平衡时边际利润由33 元/个下降为26.40 元/个, 也下降了20%,盈亏平衡时固定成本极值为零,说明单靠降低固定成本无法实现扭亏为盈。
⑤边际固定成本为零, 表明固定成本不随销售量的变化而变化, 但单位固定成本随销售量的变化而变化,并且成反比关系,销售量20 万个时,单位固定成本33 元/个;销售量25 万个时,单位固定成本26.4 元/个;销售量15 万个时,单位固定成本44 元/个。
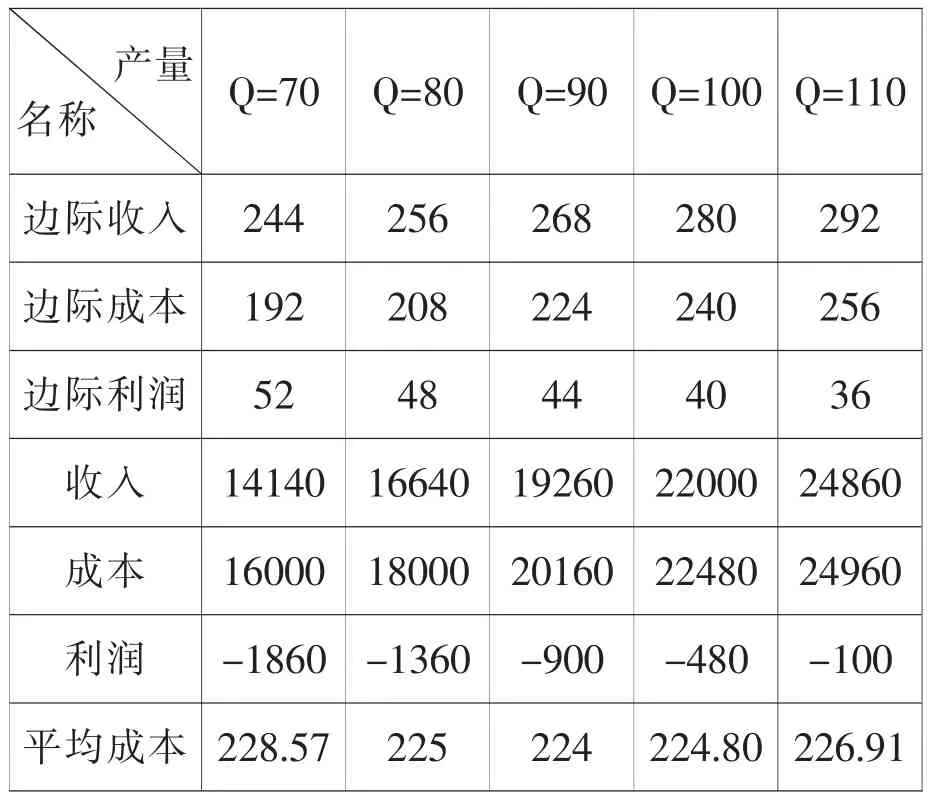
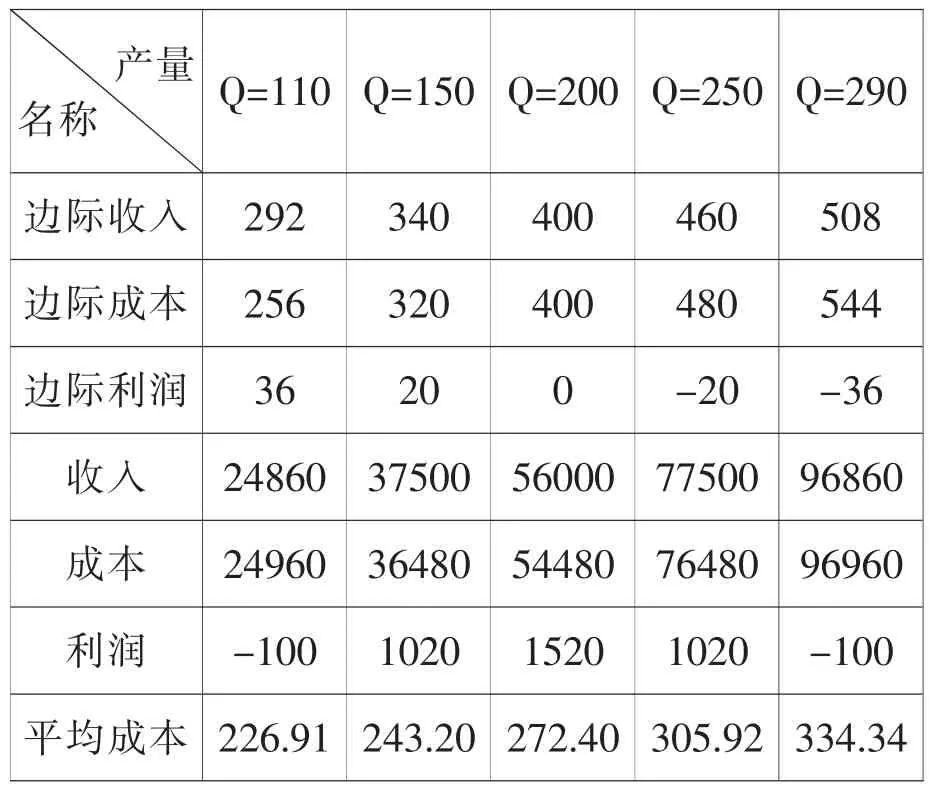
3.边际利润小于零、边际收入小于边际成本(P 分析采用的资料:产品销售价格230 元/个, 单位变动成本240 元/个, 固定成本660万元/年,销售量20 万个/年,生产能力25 万个/年。 (1)根据分析资料计算的数据 ①边际收入MS=S′(q)=P=230 元/个 ②边际成本MC=C′(q)=V=240 元/个 ③边际利润MR=R′(q)=S′(q)-C′(q)=P-V=-10 元/个 ④边际固定成本MF=F′=0 ⑥盈亏平衡时边际收入和销售价格S0′=P0=R0′+V=273 元/个 ⑦盈亏平衡时边际成本和单位变动成本C0′=V0=P-R0′ =197 元/个 ⑨盈亏平衡时固定成本F0=R′(q)·Q=-200 万元 ⑩销售收入 4600 万元 ⑪销售成本 5460 万元 ⑫销售利润 -860 万元 (2)分析 ①边际利润为-10 元/个, 边际收入小于边际成本,A 产品此时属于“负贡献”产品,销售量的增减对弥补固定成本有“负贡献”。 增加销售量,会使企业增加亏损;虽然减少销售量会使企业减少亏损, 但不管销售量如何减少, 亏损不会低于固定成本数额, 销售量为零, 亏损数额等于固定成本额, 只要有销售量,亏损数就大于固定成本数额。 ②降低边际成本(单位变动成本)是实现扭亏为盈的主要途径, 该产品的盈亏平衡时的边际成本为197 元/个,在其他条件不变的情况下,边际成本下降17.92%以上,就能扭亏为盈。 ③提高边际收入(销售价格)也是实现扭亏为盈的主要途径, 该产品盈亏平衡时边际销售收入(销售价格)S0′=P0=273 元/个,在其他条件不变的情况下,边际销售收入(销售价格)提高12.09%以上就能扭亏为盈。 ④降低固定成本,可以直接减少亏损,该产品固定成本降低20%, 盈亏平衡时边际利润由33 元/个下降为26.40 元/个, 也降低了20%。 盈亏平衡时固定成本极值为-200 万元,表明在其他条件不变的情况下,就是固定成本为零时,还要亏损200 万元。 ⑤边际固定成本为零, 表明固定成本不随销售量的变化而变化, 但单位固定成本随销售量的变化而变化,并且成反比关系,销售量20 万个时,单位固定成本33 元/个;销售量25 万个时,单位固定成本26.4 元/个;销售量为15 万个时,单位固定成本44 元/个。 通过边际原理在线性量本利经济函数的应用和实例应用分析,我们比较充分地认识到: 线性量本利经济函数应用边际原理,对线性量本利经济函数进行一阶导数的计算,不仅直接得出边际数据,简化了盈亏平衡分析的计算公式,同时也有利于对边际概念的理解,特别是再引入“PV 分析法”,使线性量本利经济函数边际分析更加简捷明确,有利于普遍推广应用,同时也符合现实统计和财务制度的要求。 这里需要特别强调:边际在线性量本利经济函数的应用,不仅限于本文例举的财务管理相关内容,只要符合线性量本利经济函数类型,包括:生产管理、管理会计、 技术经济等领域的一般经济分析、预测和决策经济分析都是适用的,在这里就不赘述。 线性量本利经济函数的一阶导数均为常数,可以根据边际计算结果和结论及“PV 分析法”进行定量定性的边际分析,而非线性量本利经济函数通过一阶导数计算, 得出的是边际函数,难以直接进行边际经济分析。这就需要边际经济的延伸应用, 将二阶导数求极值的方法应用于非线性量本利经济函数,从而形成非线性量本利经济函数边际的优化分析体系,应用利润最大化定理,解决非线性量本利经济函数中利润最大值时最优产量的计算;应用平均成本最小化定理,解决非线性量本利经济函数的平均成本最低时最优产量的计算, 从而解决非线性量本利经济函数的边际分析问题。 1.定理一般表述 在经济函数符合边际延伸应用定理的前提条件下,边际利润为零,当边际成本和边际收入相等时,实现的利润最大。此点对应的产量为利润最大时的最优产量。 2.应用定理及计算方法 设利润函数R(x),收入函数S(x),成本函数C(x) 要使MaxR(x)存在,必R(x)可导,R″(x)<0 且R′(x)=0,求得x 对应有MaxR(x) R(x)=S(x)-C(x) R′(x)=S′(x)-C′(x) 若R″(x)<0 令R′(x)=0 有S′(x)-C′(x)=0 存在MaxR(x) 3.定理的理解与思考 ①当边际成本小于边际收入时, 说明增加一个单位数量(产量或销量),会使利润逐步提高(C′(x) ②当边际成本大于边际收入时, 增加一个单位数量(产量或销量),会使利润逐步降低(C′(x)>S′(x),R(x)↓)。 ③只有C′(x)=S′(x)时,存在MaxR(x)。此点对应的产量为利润最大时的最优产量。 4.利润最大化定理的应用实例 (1)公司B 产品非线性量本利经济函数 ①收入函数S(q)=0.6q2+160q ②成本函数C(q)=0.8q2+80q+6480 ③利润函数R(q)=S(q)-C(q) =-0.2q2+80q-6480 其中q单位为套,其他单位为万元 (2)根据边际原理得出公司B 产品边际函数 ①边际收入函数MS=S′(q)=1.2q+160 ②边际成本函数MC=C′(q)=1.6q+80 ③边际利润函数MR=R′(q)=-0.4q+80 (3)根据利润最大化定理计算 ①方法一: 由于R″(q)=-0.4 <0,存在MinR(x) 令R′(q)=0 有-0.4q+80=0 则q=200 ②方法二: 当C′(q)=S′(q)时 有1.6q+80=1.2q+160 则q=200 (4)q=200 时利润最大化的最优数据 ①边际收入S′(200)=400 ②边际成本C′(200)=400 ③边际利润R′(200)=0 ④收入S(200)=56000 ⑤成本C(200)=54480 ⑥利润R(200)=1520 (5)B 产品不同产量q 时数据对比情况(详见表1) 表1 B 产品不同产量q 时数据对比情况 1. 定理一般表述 在经济函数符合边际延伸应用定理的前提条件下,边际平均成本为零,当平均成本与边际成本相等时,平均成本最低。此点对应的产量为平均成本最低时的最优产量。 2.应用定理的计算方法 设x为产量,C(x)为成本 则C′(x)为边际成本,为平均成本 要使A(x)达到最小(求MinA(x)) 必A′(x)可导 若A″(x)>0 令A′(x)= 0 求得x 对应的MinA(x) 根据商的求导法则 若A″(x)>0, 存在MinA(x) 令A′(x)=0 ∴C′(x)-A(x)=0 即C′(x)=A(x)时存在MinA(x) 3.定理的理解与思考 ①因为当边际成本小于平均成本时,说明增加一个单位的产量的成本小于原来的平均成本,则增产会使平均成本逐步降低; ②而当边际成本大于平均成本时, 说明增加一个单位的产量的成本大于原来的平均成本,则增产会使平均成本逐步升高; ③只有边际平均成本为零, 当边际成本等于平均成本时,平均成本最低,此点对应的产量为最优产量。 4.平均成本最小化定理的应用实例 (1)公司B 产品非线性量本利成本经济函数 (2)根据边际原理得出公司B 产品边际经济函数 (3)根据成本最小化定理计算 ①方法一: 则q2=8100 得q1=-90,q2=90 取q=90(q>0) ②方法二: 则q2=8100 得q1=-90,q2=90 取q=90(q>0) (4)q=90 时平均成本最小化的最优边际经济和经济数据 ①边际收入S′(90)=268 ②边际成本C′(90)=224 ③边际利润R′(90)=44 ④收入S(90)=19260 ⑤成本C(90)=20160 ⑥利润R(90)=-900 ⑦平均成本(90)=224 (5)B 产品不同产量q时数据对比情况(详见表2) 表2 B 产品不同产量q 时数据对比情况五、边际原理在非线性量本利经济函数的应用与思考
(一)利润最大化定理的应用与思考
(二)平均成本最小化定理的应用与思考