基于增强学习的机械臂轨迹跟踪控制

刘卫朋，邢关生，陈海永，孙鹤旭

( 1.河北工业大学 控制科学与工程学院,天津 300130； 2.青岛科技大学 自动化与电子工程学院，山东 青岛 266042)

0 引言

机械臂动力学具有高度非线性和不确定性，目前针对机械臂轨迹的跟踪控制问题已有很多可行的控制方案。为了便于设计且成本低廉，工业界习惯采用比例—积分—微分(Proportion Integration Differentiation, PID)控制器设计方法，然而传统PID控制方法对不确定的工作环境、负载变化和未知外部扰动的适应能力不足，需要采用先进的自适应技术来提高控制器的工作性能。

近年来增强学习(又称强化学习)逐渐受到研究者的重视。增强学习是一种非线性系统的直接自适应最优控制方法[1]，该方法计算简单，能够赋予控制器学习能力，使控制器灵活应对变化的外部环境。增强学习控制器通过与环境(包括动态模型未知的被控对象)相互作用，基于实际运行数据学习控制律，目的是获得最大的长期回报，即使控制系统性能最优。增强学习控制器设计不需要被控对象的动态模型，控制动作的产生是基于当前或历史数据。已有一些研究工作将增强学习算法应用于机械臂控制，例如，文献[2]采用基于K-均值聚类的增强学习方法解决机械臂的避碰问题;文献[3]采用Q-learning算法解决机械臂关节运动的轨迹跟踪控制问题，研究增强学习中的各种函数逼近技术，对比了模糊Q-learning控制[4]、神经网络Q-learning控制[5]、决策树Q-learning控制[6]、支持向量机Q-learning控制[7]在负载变化、力矩扰动情况下的平均偏差、最大偏差等性能指标。

采用增强学习直接完成机械臂的控制存在两方面困难[8-9]：①初始参数较难选择，系统容易出现不稳定，工程上难以实现；②增强学习算法在应用于连续系统的控制任务时，面临着因状态空间巨大而带来的值函数泛化问题，即如何存储和逼近一个蕴含着最优控制目标的函数。本文提出基于SARSA(state-action-reward-state-action)算法的增强学习补偿控制策略，并与传统PD控制组合使用，利用PD控制完成基本的镇定任务，利用增强学习算法实现对未知干扰因素的补偿，从而提高对不同情况的适应能力。

1 机械臂轨迹跟踪控制问题

在机械臂的轨迹跟踪应用中，无论是令机械臂末端运动到某个或某几个位置点，还是令机械臂末端以某姿态沿给定轨迹运动，常常需要完成轨迹规划和轨迹跟踪两步计算任务。轨迹规划指利用机械臂的逆运动学模型，根据期望的末端位姿计算出各关节的期望转角，进而规划出各关节角和角速度随时间变化的曲线。由于现实物理世界存在各种不可预测的干扰和不确定因素，规划出的轨迹在执行过程中很容易偏离，需要实时根据关节角、角速度的测量值和期望值之间的偏差进行调节，使机械臂的各个关节尽可能按期望轨迹进行旋转运动，这是轨迹跟踪控制问题。

机械臂关节运动的轨迹跟踪控制属于多变量控制，机械臂关节间存在非线性耦合，而传统的PD控制虽然容易实现，但是任何一个作用于单一关节的PD控制器都难以克服其他关节带来的干扰，控制性能不佳。之后出现的基于模型的计算力矩控制、鲁棒控制和自适应控制等方法大多需要已知机械臂的数学模型，然而大多数机械臂数学模型复杂、模型参数很难测定或代价较高，从而制约了这些高级控制方法的应用。实用的解决方案是采用PD反馈与动态补偿相组合的控制策略，或者PD反馈与逆模控制相组合的控制策略。

Lewis[7]使用三层前馈神经网络进行非线性补偿，与PD控制器共同构成机械臂的轨迹跟踪控制系统，控制系统基本结构如图1所示。神经网络用来逼近一个类似于计算力矩控制的控制律[8-9，11]。Ren等[12]为抵抗神经网络逼近误差给跟踪控制带来的影响，提出带有滑模控制的神经网络鲁棒补偿控制器，Xie等[13]完成了五自由度机械臂自适应神经网络控制器的设计和分析，并通过MATLAB/ADAMS联合仿真验证了方法的有效性；王良勇等[14]在系统离散化的情况下，将关节间的耦合影响看作干扰，使用径向基函数(Radial Basis Function, RBF)神经网络逼近单个关节的干扰项，分散地实现了机械臂各关节的补偿控制。

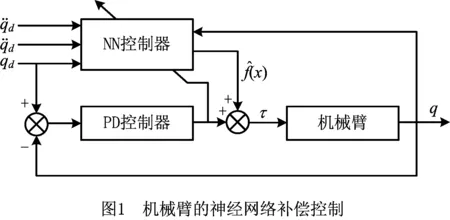
另外，PD与逆模控制的组合控制策略是利用逆动力学或逆动力学的近似动态消除机械臂的非线性，将控制系统变换为二阶线性系统，利用极点配置方法可设定PD控制器参数。基本控制框图如图2所示。Pane等[15]采用执行者—评价者结构的增强学习算法补偿PD控制器，每个关节有一个增强学习控制器，但是控制系统结构比较复杂；Spong等[16]在其基础上提出改进的控制器设计方案，以克服对惯性矩阵估计限制的条件；Kim等[17]采用多层前馈神经网络和一个镇定的反馈控制器组合的控制方案，反馈控制器用于保证系统有界，前馈神经网络以在线学习的方式逼近机械臂的逆动态，形成直接逆控制器；Tian等[18]采用递归神经网络逼近两自由度柔性机械臂的逆模型，进而实现逆模控制；Fahmy等[19]将模糊神经网络用于机械臂逆动态建模，与模糊PID伺服控制共同构成机械臂控制系统；Ouyang等[11]对单轴柔性机械臂直接采用执行者—评价者结构的增强学习算法设计控制器，以保证系统在学习初期的稳定性，但是执行者和评价者的神经网络初始参数难以选择。

补偿控制和逆模控制均可消除关节间耦合和重力作用产生的非线性项给控制系统带来的反面作用，但是缺少对控制系统最优性方面的考虑。本文采用增强学习这种自适应最优控制方法设计PD伺服控制的补偿控制器，通过增强学习的自适应能力，使其能够灵活应对关节间的耦合作用和不确定外部扰动，在控制过程中逐渐学习出令输出误差和控制输入最小的补偿控制律。

2 增强学习基本原理

2.1 增强学习的方法框架

增强学习是一个智能体从经验数据中学习出控制或决策策略的过程，其经验来自于系统运行过程中环境给智能体回馈的奖励或惩罚。奖励可被看作是正向的增强信号，惩罚被认为是反向的增强信号，这种增强信号是对智能体在某一状态下所采取的控制动作的评价(正面或负面)。试错过程中，智能体在历史经验中增强信号的刺激下，不断选择能够在未来取得最多报酬的控制动作，即寻求报酬最大化，这是对生物界常见行为的模拟。

增强学习系统的基本框架如图3所示，交互过程中的3个基本信号分别为状态、控制动作和报酬。状态指智能体所面对的外部环境的状态；动作是智能体做出的决定，施加在外部环境上，影响其状态变化；报酬是动作被执行后产生的效果的反馈。从控制的角度看，智能体可被认为是控制器，外部环境被看作被控对象，动作是基于状态计算出的控制输入，报酬信号由成本函数定义，控制成本减小是报酬，控制成本增大是惩罚，即目标是追求控制成本最小化。

2.2 SARSA算法

SARSA算法是一种“在策略”(on-policy)的TD(temporal-difference)算法，状态—行为值函数的估计和更新依赖于当前策略和状态—行为对。通过对比两种算法值迭代的过程，能够很容易地理解SARSA与Q-learning的区别。一步SARSA的值函数迭代规则为

Qt+1(xt,ut)←Qt(xt,ut)+

α[rt+1+γQt(xt+1,ut+1)-Qt(xt,ut)]。

(1)

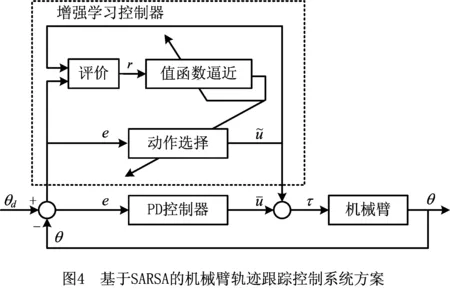
3 基于SARSA算法的机械臂轨迹跟踪控制策略

3.1 控制器结构设计

机械臂轨迹跟踪控制系统采用PID和增强学习控制组合的控制系统结构，如图4所示。

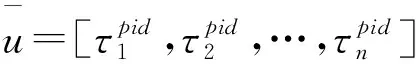
3.2基于SARSA算法的补偿控制策略

(2)

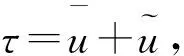
(3)

期望值d已知,设式(3)可离散化为

(4)

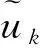
设折扣型最优值函数为

(5)

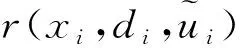
(6)

式中：ei=di-xi为跟踪偏差，矩阵Q和R为对角矩阵且正定。式(4)的最优值函数的迭代形式为

V*(xk,dk)=

(7)

在增强学习框架下，采用状态行为值函数的定义

(8)

则最优状态行为值函数为

(9)

由式(7)和式(9)可知

(10)

寻找控制律就是为了计算出令最优状态行为值函数的值最小的控制输入。设最佳的控制律为h*(xk,dk)，则

(11)

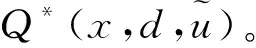
(12)

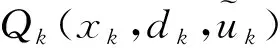
3.3 Q值函数存储与学习

本文采用一种具有内部反馈结构的递归型神经网络来提高迭代的速度，该网络与已有研究工作所采用的前馈神经网络不同，具体结构如图5所示。这种神经网络包括输入层、隐层和输出层3层，其隐层神经元的输出被反馈至输入层，这是与前馈神经网络不同的地方。

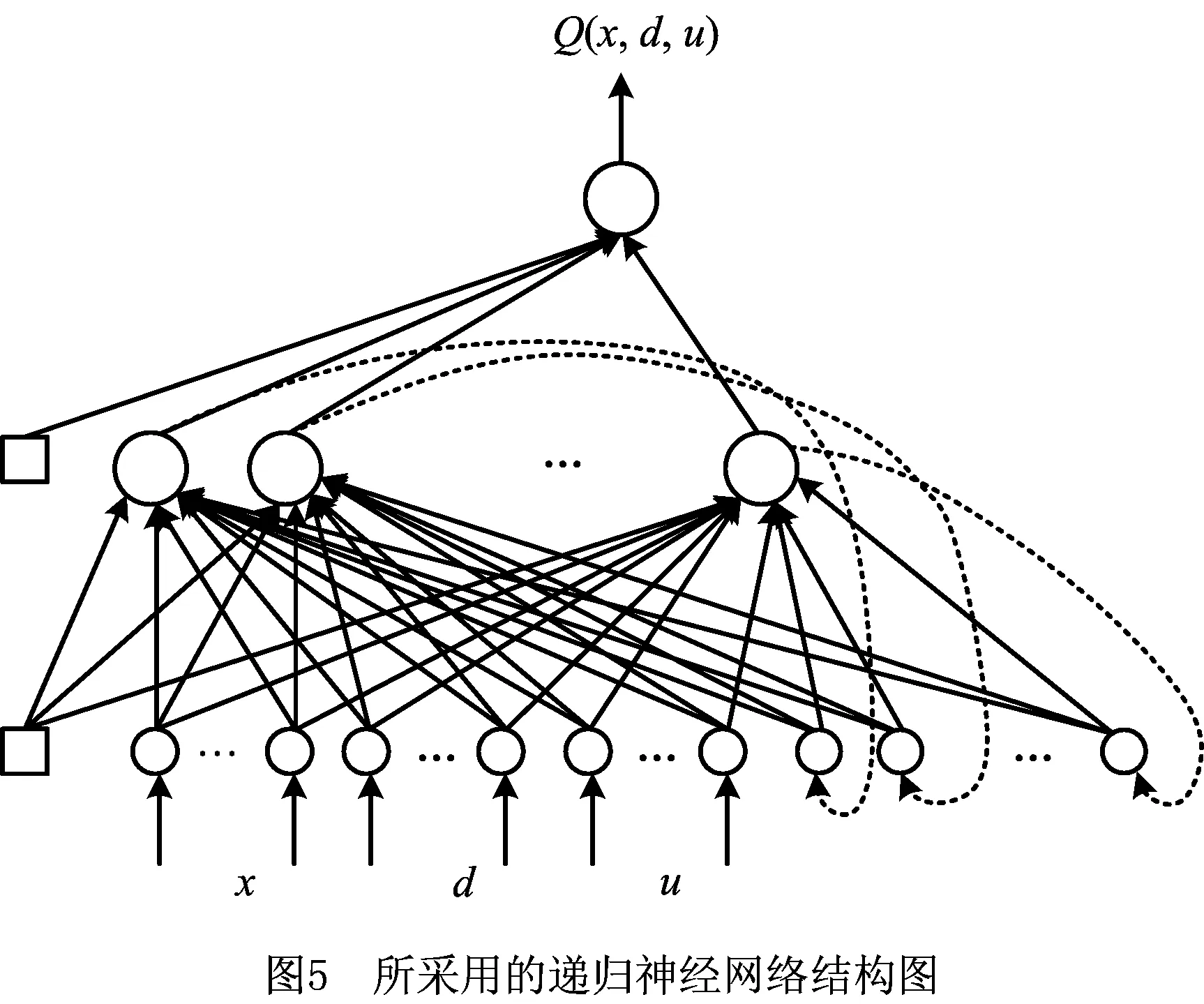
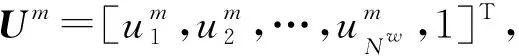
令v=[v1,v2,…,vNH,φ]T为从隐层到输出层的权重，其中：vj表示第j个隐层单元到输出层的权值，φ表示输出层神经元的阈值。隐层的激活函数采用非线性sigmoid函数表示为

(13)

需要解释的是，如果式(13)中的a为列向量，则φ(a)表示分别以a中各元素为自变量，执行式(13)的计算而得的列向量。输出神经元的激活函数是线性的。则神经网络所能存储的值函数可参数化地表示为

(14)

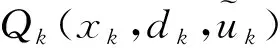
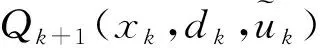
(15)

根据反向传播算法，先根据式(16)更新权重vj：

(16)

然后根据式(17)和式(18)更新权重wij：

(17)

(18)

类似地，神经元阈值φ和θj的更新律分别为：

(19)

(20)

式中ε和γ分别为输出层和隐层的学习率。

3.4 动作选择

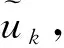
(21)

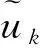
(22)

l=4n+i，i=1,2,…,n。

(23)

4 仿真实验

4.1 实验设定

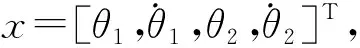
神经网络的结构选择对增强学习控制器的设计非常重要。对于两关节机械臂，神经网络外部输入的个数NI=10，包括两个关节的位置与速度4个量、期望位置与速度4个量，以及控制力矩2个量，隐层神经元个数选择为NH=20，则递归神经网络输入层的神经元个数Nw=NI+NH=30。由网络结构可知，输入层到隐层的权重W是31×20矩阵，隐层到输出层的权重v是21×1向量，这里的权重包含了各神经元的阈值参数。神经网络权重W和v中各元素的初始值是在[-0.1,0.1]区间内随机产生的。

4.2 跟踪控制仿真实验

仿真实验首先设计能够使机械臂稳定的PD控制器，然后增加增强学习补偿控制，并对比分析增强学习控制的作用。

设计两个PD控制器，分别操纵机械臂的两个关节，PD控制器的算式为

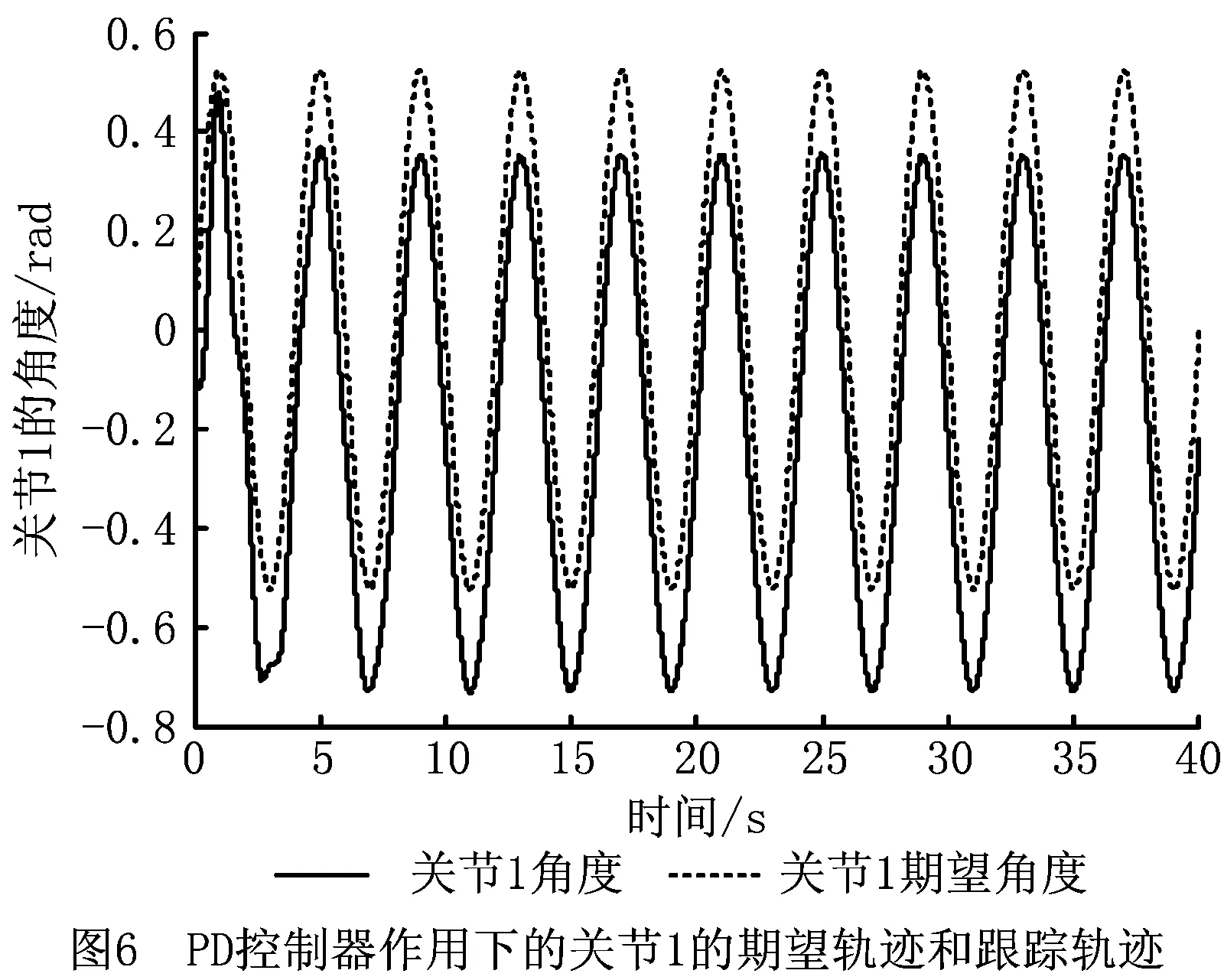
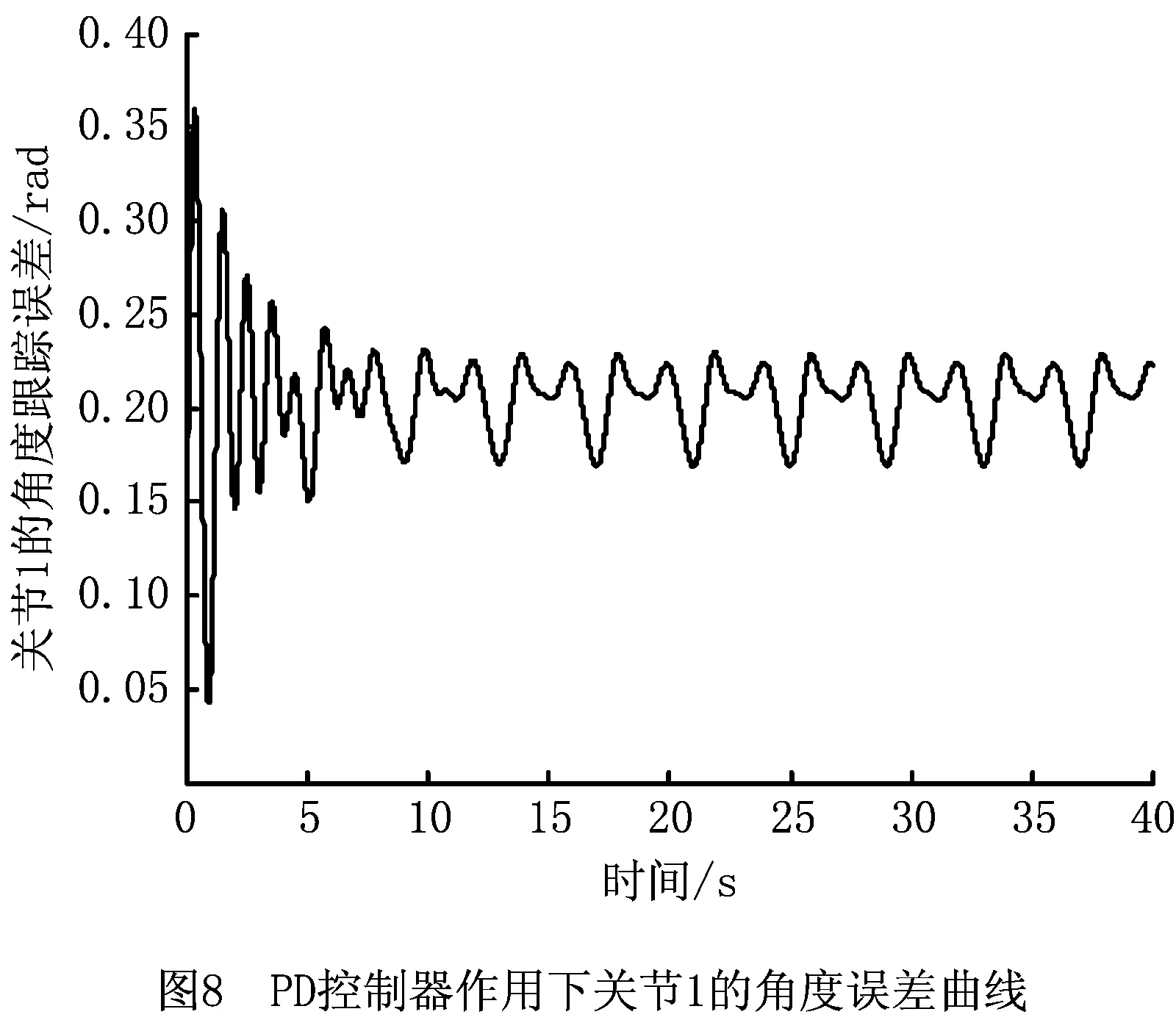
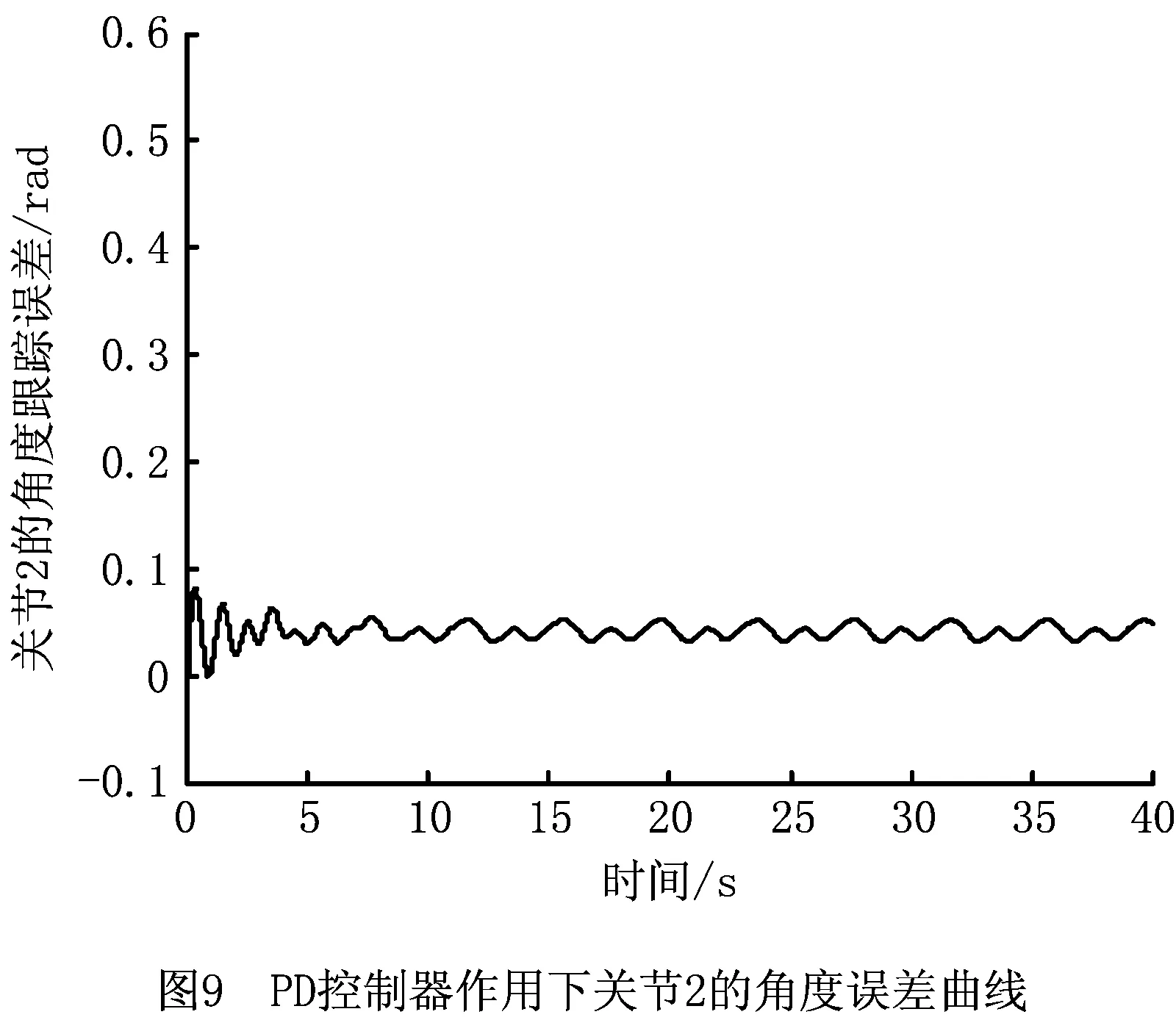
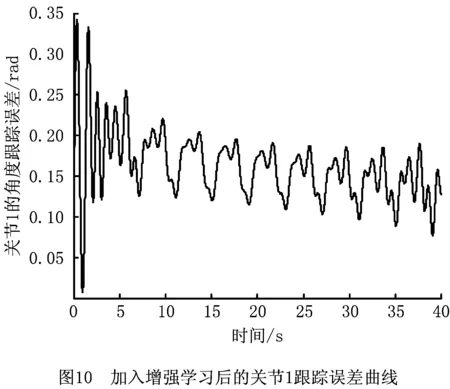
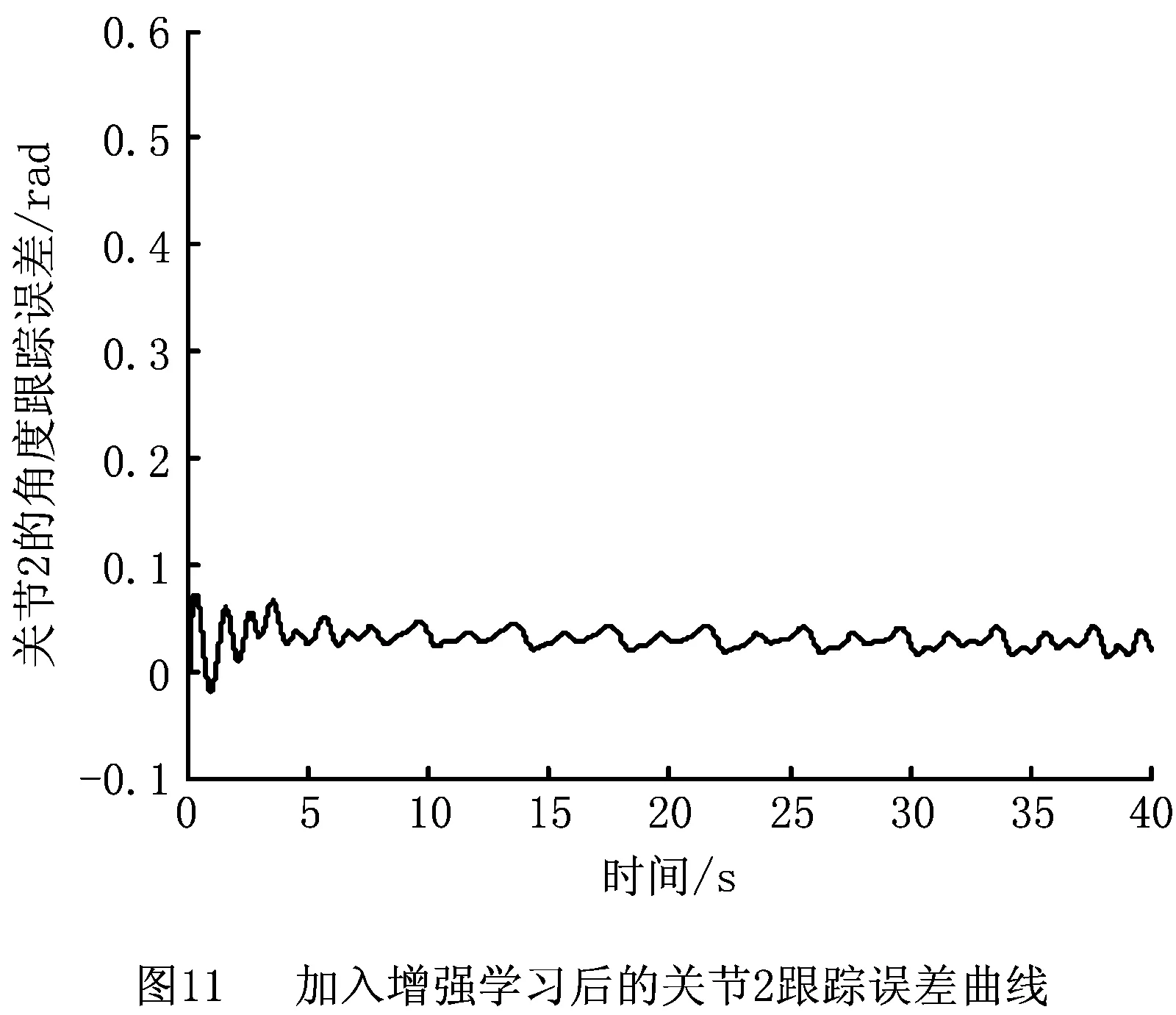
PD控制是机械臂稳定的基础，通过增强学习控制器的补偿作用能够减小跟踪误差。跟踪曲线的周期性可以使增强学习进行重复学习，且每次学习均在前次学习的基础上更新存储Q函数的神经网络权重。加入增强学习补偿控制后，机械臂两关节角的跟踪误差轨迹分别如图10和图11所示。

为了说明增强学习的补偿作用，将两次仿真实验结果放置在一个坐标系内进行比较，如图12和图13所示。

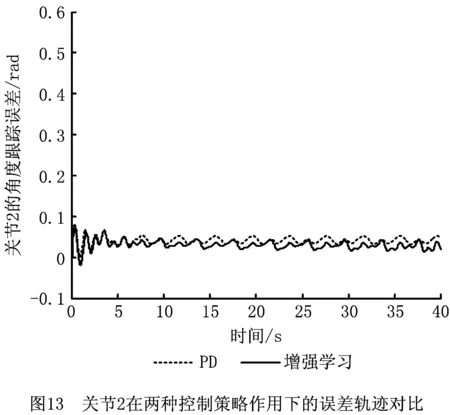
由图12和图13可见，在加入增强学习控制器后，两个关节角的跟踪误差均减小，而且由于增强学习的持续学习作用，每个学习周期后，与前一学习周期相比，误差在逐渐减小;而单纯的PD控制下，误差变化也存在周期性重复。这是增强学习控制学习能力的主要表现。

5 结束语

本文针对两自由度机械臂的控制问题，提出一种基于SARSA算法的机械臂轨迹跟踪控制策略，通过与传统PD控制组合使用，利用PD控制完成基本的镇定任务，利用增强学习算法实现对未知干扰因素的补偿，可以提供对不同情况的适应能力。因为PI控制的积分作用使控制速度变慢，系统稳定性变差，不适用于工业机器人，所以本文的PID控制器使用PD控制算法，以增强学习控制器作为补偿控制。仿真实验表明：

(1)引入增强学习后，机械臂可实现自主控制。控制器在连续空间内产生实值型控制量，提高了控制精度。

(2) 通过仿真实验验证了自适应离散化的强化学习方法在机械臂轨迹跟踪问题中的可行性和有效性，明显提高了控制器的学习速度。