敢问路在何方，路在脚下*——高三学生解题困惑的分析与对策

●

(通渭县第二中学,甘肃 通渭 743300)

有些高三学生在二轮复习中，总觉得自己已掌握基本的解题思想与解题技能，但在后阶段的诊断考试中成绩一直徘徊不前，感觉力不从心、事与愿违，以致于对自己的能力产生怀疑，造成自信心不足，缺少动力.“老师讲解能听懂，自己独立不会做”“一看有思路，一做就出错”“解答题有得分，不能得高分”等问题成为制约学生成绩的常态因素.好多学生考试后发现许多错题其实不该错，但考场出现思维受阻，考后思路清晰，豁然开朗.学生经常会问自己：“这么简单的问题怎么就没想出来，怎么就得不了分？”笔者针对学生存在的问题逐一分析和诊断，并给出教学对策，供师生在高考复习中参考与借鉴.

1 优柔寡断，缺失抉择

笔者通过调查发现：学生面对一题多解问题时，得分不理想的原因在于缺少对各种方法的比较，以及对诸多方法优缺点的分析和预判后的合理抉择，学生往往匆忙选择自己所熟悉的一种方法，结果“半途而废,屡战屡败”.因此，学生应该明白：一方面，受考查目的与功能的限制，考题会有意识地考查某种方法；另一方面，即使一题多解，但解题过程、运算的复杂程度有差别，若考生不思抉择，势必出现“有思路，操作不下去”“能操作，出错风险高”的困惑感，正确选择方法是成败的关键.

例1已知函数f(x)=|x2+3x|，其中x∈R,若方程f(x)-a|x-1|=0恰有4个互异的实数根，则实数a的取值范围是______.

(2018年甘肃省定西市第一次数学高考诊断试题第16题)

解方程|x2+3x|=a|x-1|有4个互异的实根，则

x2+3=a(x-1),

或

x2+3x=-a(x-1)，

即一元二次方程x2+(3-a)x+a=0与x2+(3+a)x-a=0分别有两个根.由Δ>0，得09.

对策要学会抉择，首先必须弄清楚每种方法得以顺利实施的前提条件，以判断函数在某区间上的零点个数为例，此类题的主要方法有4种:1)直接解方程(简单方程);2)构造两个函数图像的交点(函数图像能画出);3)图像与x轴的交点个数(能大致画出函数图像，分析图像走势);4)零点存在性定理，这4种方法选择的标准显然已见.其次教师在复习教学中通过题组有意识地训练学生抉择的能力，在课堂中让学生交流、讨论、辨析与质疑，让学生自己说出选与不选的理由，只有知道选择的理由，才能有的放矢(其他方法)，游刃有余.

2 望风扑影,缺失目标

学生在解题中感觉问题是熟悉的，方法也能马上入手，但走着走着就迷失了方向，造成这种现象的主要原因是缺失目标.漫无目的主要表现为:一是走到某一步，但没有弄清楚下一步的子目标是干什么；二是一开始审题时就没有盯紧目标，带着目标寻找更为合理的解题思路，导致自己选择的方法虽可行，但后续的演算变形复杂以致迷失方向.

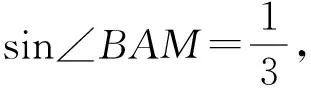
(2018年甘肃省兰州市第一次数学高考诊断试题第16题)

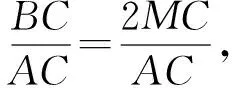
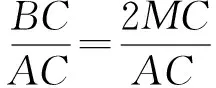
tanβ=2tan(β-α),

从而

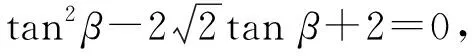
即

故

对策解题就是先明确题目条件，再紧盯目标实施解题步骤的过程.为提高强化学生的目标意识，首先在典例讲解时，学生要独立完成审题，紧接着教师实施3个追问：1)依据解题目标，你会设计出怎么样的解题流程，此流程通过哪些步骤可以实施；2)这个流程是否存在可以调整的地方；3)能否减少其中几个子目标，使过程更简洁.经过训练学生才会养成从目标出发思考问题的习惯.其次，要指导学生养成根据各个子目标来书写解题过程的习惯，某些问题的子目标除了用符号和式子表达外，还需要适当的文字语言，这样做既检测了整个解题思路正确与否，也便于解答题步骤过程得分.

3 墨守成规,缺乏意识

就高三学生而言，经过较全面、系统的复习，不缺知识也不缺方法，但常常由于缺乏应用这种方法的意识从而造成得分困难.“缺意识”学生的直观感悟是当时“没想到”，但稍加提示后恍然大悟，主要原因有两个：1)常常会被一些表面的、带干扰的信息所迷惑，导致看不出问题的本质，思维受阻，想不起具体的操作方法；2)面对熟悉却有变化的问题，因抓不住变化点而显得无所适从.

例3设a,b∈R,则a>b是a|a|>b|b|的

( )

A.充分不必要条件 B.必要不充分条件

C.充要条件 D.既不充分又不必要条件

(2018年甘肃省兰州市第二次数学高考诊断试题第5题)

分析此题入手容易，即判断两个互逆命题的真假，真命题要给出必要的推理说明，假命题能举出反例，但学生的得分率较低.其原因是去掉绝对值符号后，分类情况太多了，学生转而一想会不会是假命题，就试着去举反例但又举不出来，最后只好凭感觉选出选项.笔者启发学生“a|a|,b|b|有何共同点，是由什么得到的”，这时学生才意识到需要构造函数y=x|x|，进一步只需判断出函数的单调性便可同时判断两个命题的真假.经判断，函数y=x|x|在定义域R上是增函数，故选C.

对策要养成良好的解题意识，首先离不开多次、反复的强化与训练，因此对所做的试题要进行归纳、总结、类比，多做有关的相似联想.其次，需要强化“变式训练”，在训练中要注意两点：1)要帮助学生分析“变式题”中的变与不变；2)鼓励学生主动参与变通，以多变应不变，在第二轮复习中，将同类试题进行归纳与整理，并不定期进行交流与展示.

4 重蹈覆辙，缺失感觉

缺乏感觉主要表现在两点：1)经常性在容易出错的地方犯相同的错误，潜在的原因是答题缺少节奏感；2)对代数式、图形等数学对象中所蕴含的特殊信息麻木、不敏感，即感知不到解决问题的突破口.

例4若函数f(x)=(1-x2)(x2+ax+b)的图像关于直线x=-2对称，则函数f(x)的最大值为______.

(2018年甘肃省兰州市第二次数学高考诊断试题第16题)

分析此题学生主要存在两个问题：一是学生缺失对特殊点的感觉，不会求解a,b的值；二是即使求出a,b的值，选择用导数来求最值，运算量大，困难重重，半途而废.学生若能敏感地捕捉出其中的两个特殊信息，则“拿下”此题便游刃有余，这样的解题经验靠的就是良好的感觉.

解观察发现f(x)的两个零点为x=-1和x=1，由f(x)的图像关于直线x=-2对称，可得f(x)的另两个零点为x=-3和x=-5，从而

f(x)= (1-x2)(x+3)(x+5)=

-(x-1)(x+1)(x+3)(x+5).

其次，可将函数的解析式变形为

f(x)=-(x2+4x-5)(x2+4x+3),

换元后可化归为二次函数的最值.令t=x2+4x∈[-4,+∞),则

f(t)=-(t-5)(t+3)=-(t-1)2+16,

故f(x)的最大值为16，此时

对策学生要有良好的解题感觉，首先要把握好解题节奏，关键处要放慢一些、易错处要细心一些、衔接处要留心一些，如三角函数中的“合一变换”，既然知道易在角度的配凑上出错，就应该更加仔细；又如解圆锥曲线的综合题，知道几何条件代数化是一个重要环节，就应该在运算变形上突破下功夫.其次要善于发现“隐含信息”,如数字的特殊性、图形的对称性、代数式的结构性等常常会让我们意外收获简洁、优美的方法.

5 一意孤行，缺乏规范

高三学生规范的缺失也是失分的主要因素，包括审题不规范、解题不规范、书写不规范、时间分配不规范等.由于审题不规范，对题设条件视而不见，丢三落四;由于解题不规范，思维跳跃，缺少逻辑，推理不严;由于书写不规范，环节不齐全，步骤不完整；由于时间分配不规范，会做题没时间作答，抓了芝麻，丢了西瓜，最后只是“颗粒归仓”.

对策审题规范要迅速抓取已知条件、隐含条件，并做好重点记号，反复推敲已知条件帮助思考并形成思维；书写规范要避免将答题卡当作稿纸，随心所欲；解答规范要求逻辑严密，论证有据，层次清晰，详略得当.

总之，部分高三学生的解题存在困惑，通过对错题的总结分析，有效地克服畏惧心理，抓住已知条件，带着解题目标与意识，增强数学问题感知，合理选择简洁、高效的方法.平时多总结和归纳，多问为什么，讲求方法——敢问路在何方，其实路就在脚下！