三角形“四心”坐标表示及其应用*
2018-09-07
●
(广州大学数学与信息科学学院,广东 广州 510006)
●关丽娜
(深圳大学数学与统计学院,广东 深圳 518060)
三角形“五心”的向量表示指的是如下定理:
定理1在△ABC中,设P是三角形所在平面上任意一点,则
(1)
其中S△PBC,S△PCA,S△PAB表示有向面积.这个既有面积又有向量的等式(1),称为三角形“五心”的向量形式.它将三角形“五心”的向量表达式统一起来.这里的“五心”指的是三角形的重心、内心、外心、旁心、垂心.
从形式上看,上述定理当属三角形“五心”的一个几何刻画.我们知道一个数学研究对象如果具有几何和代数上的两种刻画,那么该对象从某种程度上来说是优美的.“数形结合”思想说的就是这样的一种数学美.
数学具有美,三角形“五心”是其中一种数学美.那么用纯坐标(不涉及角度、边长)表示三角形“五心”的坐标也应该有它的优美.遗憾的是,国内少见有对三角形“五心”纯坐标形式进行刻画的文献(对于三角形外心和垂心的代数刻画可参见文献[1]).本文介绍Wildberger教授在文献[2]中引入的符号在刻画三角形重心、外心、垂心、九点圆圆心的坐标表达式中的应用.这种刻画是代数的,笔者利用三角形重心、外心、垂心的坐标表示给出了三角形重心、外心、垂心三点共线的一个证明.
1 符号的规定及例子
Wildberger教授在文献[2]第29页中引入了以下记号:
(2)
符号(2)等号的右边是一个3阶行列式.根据行列式运算法则,得
不失一般性,我们可以定义如下更一般的符号:
(3)

我们先看一些例题:
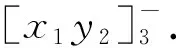

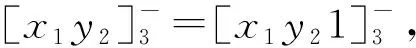
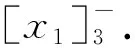
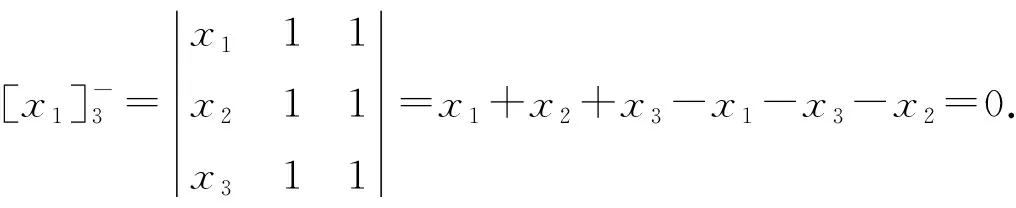


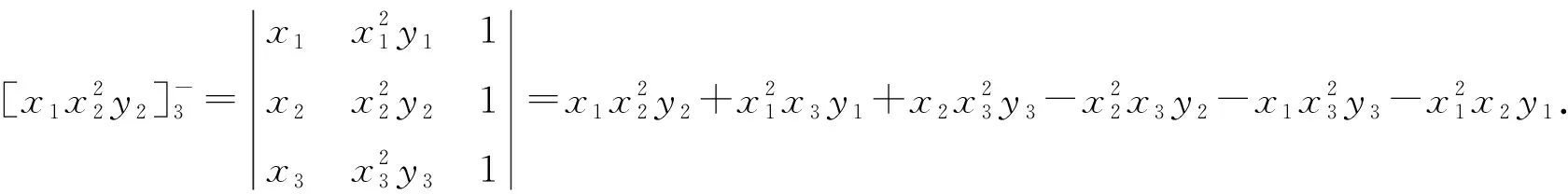

证明若直线li:Aix+Biy+Ci=0(其中i=1,2,3)三线共点,则
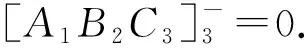

证明由三角形的面积公式可得

评注由例4和例5可知,在式(2)的使用下,三线共点和三点共线的充要条件变得异常简单.
2 符号在表示三角形重心、垂心、外心、九点圆圆心中的应用
有了式(2)的规定,我们可以得到三角形重心的坐标表示,即以下的命题(重心的横坐标详见文献[1]):
命题1设△ABC顶点A,B,C的坐标分别为(x1,y1),(x2,y2),(x3,y3),则△ABC的重心坐标为
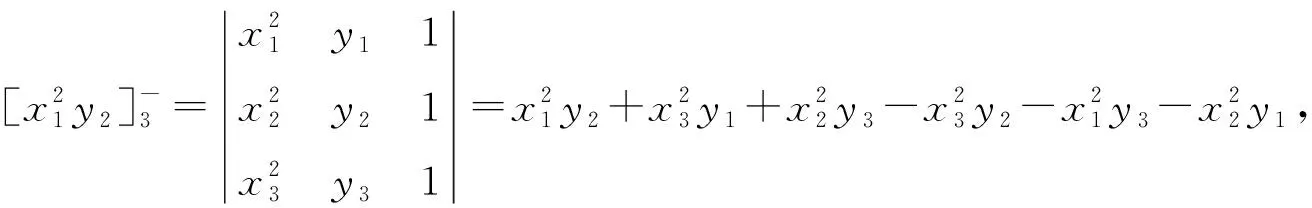

(x1+x2)x1y2+(x1+x3)x3y1+(x2+x3)x2y3-(x2+x3)x3y2-(x1+x2)x2y1-(x1+x3)x1y3=
(x1+x2+x3)(x1y2+x2y3+x3y1-x1y3-x3y2-x2y1),


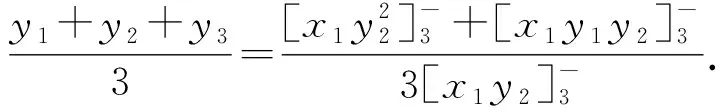
对应于三角形的外心和垂心,有以下两个命题,证明过程详见文献[2].
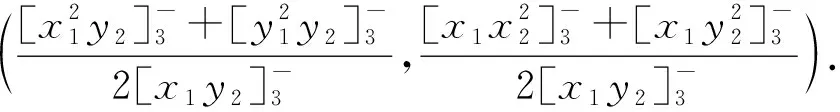

若设△ABC各边中点分别为D,E,F,各顶点到对边的垂足分别为M1,M2,M3,设△ABC的垂心为H,且设HA,HB,HC的中点分别为N1,N2,N3,则由九点共圆定理可知点D,E,F,M1,M2,M3,N1,N2,N3在△DEF的外接圆上.用式(2),我们还可以给出这个九点圆圆心的一个坐标表示,即以下命题.X为实心圆点,其证明过程与命题2类似,不再赘述.
命题4[2]设△ABC顶点A,B,C的坐标分别为(x1,y1),(x2,y2),(x3,y3),且设线段BC,CA,AB的中点分别为D,E,F,则△DEF的外心为
有了三角形的重心、外心、垂心的坐标表示,接下来我们给出三点共线的一个证明.
定理1[3]△ABC的外心、垂心、重心三点共线(欧拉线).
证明设△ABC顶点A,B,C的坐标分别为(x1,y1),(x2,y2),(x3,y3),且△ABC的重心、垂心、外心分别记为G,H,O,则由命题1~3可得点G,H,O的坐标分别为

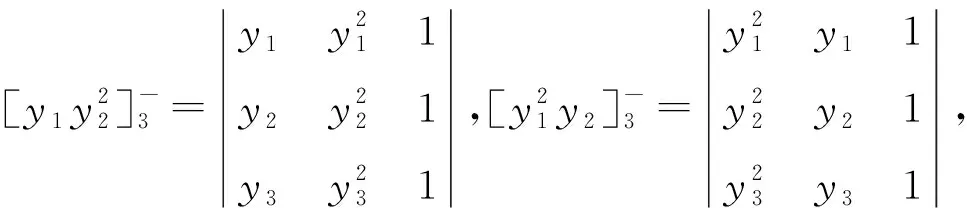

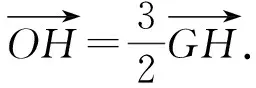
故点G,H,O共线.
从上面的讨论过程可以看出:和三角形的五心向量表示一样,可以用纯坐标(不涉及边长和角度)将三角形的重心、外心、垂心、九点圆圆心优美地刻画出来.截止目前,笔者依旧没有找到三角形内心的纯坐标表示的相关资料,它是不是也可以用式(2)优美地表示出呢?有兴趣的读者可以自己探讨.
